- ...となるものを選ぶ5.1
- Lagrangeの未定乗数
を用いて,幾何学的な境界条件も含めた変分原理の定式化も可能であり,
その場合には重みや近似解の選択はかなり自由になる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
このGalerkin形式のことを(力学以外の問題5.2
- 仮想仕事の原理は前述のように,境界値問題の純粋に数学的な表現の
一つに過ぎないから。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
と5.3
- 重み(仮想変位)の方は試験関数
と呼ばれるが,最近は重みだけでなくすべてを試験関数と呼ぶ
ようだ。ちょっと抵抗がある。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
正確には2部材の図心の位置も揃っている5.4
- そうでないと軸力の問題と曲げの問題が連成していまうことを
思い出そう。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
と5.5
- 正直な話,第1著者は変分法の学部の授業は全く理解できなかった。4年生で
配属されたあとで使うようになった仮想仕事の原理の勉強で,ちょっと
わかるようにはなったが,米国で習った応用数学の変分法も
また理解できず,1週間のtake-home-examの答を求めることが
できなかった。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... HREF="s2node7.html#chap:6">6では安定5.6
- 実は式(3.49)でPoisson比の範囲を求める際に
既に用いている。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...)の速度で厳密解に収束している5.7
- 図は両対数だから,傾きが式(
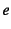 )の
)の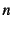 に相当する。
に相当する。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
真実と事実を区別5.8
- 第1著者の中学校担任の丸山眞先生に
教えてもらった。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
 5.9
5.9
- もちろん定量化するためには数値解析を併用するかもしれない。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
 5.10
5.10
- もちろんプログラムを作るためには解析的な結果がまず必要。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
と総称6.1
- 「微小(infinitesimal)」に対してのfinite(有限)であって,「限りが
有る」という意味ではなく,大変位理論
と等価である。ただ,大変位理論という言葉はあまり使わない。
変位が大きくなると一般的には変形(ひずみ)も大きくなり,弾性範囲での
定式化の意味が無くなるからである。
変形も大きい範囲を扱うのは大変形理論
と呼ばれる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
ことができるかについて,簡単な剛体バネモデル6.2
- 東京大学の
堀井秀之教授の示唆による。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
回転バネ6.3
- 機械式の時計の中で見た人もいると思う。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...のような変数係数の微分方程式6.4
- 国家公務員試験の2次試験に誘導過程が出題されたことがある。
やはり,第1著者は国家公務員にはなれないと思った。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...と6.5
- バネ定数の
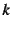 と区別するために添え字
と区別するために添え字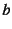 を用いているが,
慣例では添え字を付けない。また,梁の剛性行列
を用いているが,
慣例では添え字を付けない。また,梁の剛性行列
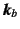 と
混同しないこと。
と
混同しないこと。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
まずは二つの特別な場合6.6
- 新しい式を得た等のときに,それが正しいかどうかを確認するためには,
極端な場合を想定するといい。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
力6.7
- 式(5.53)の第3項にあるような外力ポテンシャルが
定義できる力を保存力
と呼んでいる。追随力のような力は,
外力仮想仕事は定義できるがポテンシャルを定義できないので,
非保存力と呼ばれる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...と6.8
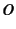 (`Big Oh')という記号はLandauの記号と呼ばれ
(`Big Oh')という記号はLandauの記号と呼ばれ
と書いたときには
になるような正の数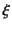 と
と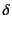 が存在することを意味する。
が存在することを意味する。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...\/)の「接線」係数行列6.9
- 式(6.54)の誘導でも考えた
増分理論的な扱いに基づいた接線係数のこと。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...iwakuma2等6.10
- あるいは付録-Eを
参照のこと。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
使った微小たわみ角の近似を用いなければ支配方程式6.11
- 誘導に
ついては付録-Eを参照のこと。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
何らかの数値解析法6.12
- 数値解析手法に
ついても付録-Eを参照のこと。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
に相当する物理量6.13
- 非圧縮性流体の静水圧
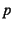 も,体積不変といった制約条件を汎関数に
組み込むときのLagrangeの未定定数に相当する物理量である。
も,体積不変といった制約条件を汎関数に
組み込むときのLagrangeの未定定数に相当する物理量である。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...と7.1
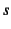 方向のせん断応力のつり合いは最終的な合応力Saint-Venantの
ねじりモーメントのつり合いに相当するので,ここでは考えない。
あるいは
方向のせん断応力のつり合いは最終的な合応力Saint-Venantの
ねじりモーメントのつり合いに相当するので,ここでは考えない。
あるいは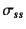 の様子がわからないので無視すると考えてもいい。
の様子がわからないので無視すると考えてもいい。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
多分にここの記述は,結果を知っている者の詭弁7.2
- 山口瞳が`debate'を
こう訳して(あるいは誰かがそう訳すということを記述して)いるのは興味深い。
出典は彼の随筆だったと思うが,正確な情報は忘れた。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
ある7.3
- ねじり定数比と呼ばれる[117]ことも
あるが,
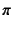 が乗じられたりそうでなかったりするので
注意する。
が乗じられたりそうでなかったりするので
注意する。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...は連続する必要は無く7.4
- この説明はわかり難いだろうか。Timoshenko梁の剛性方程式(D.18)を
誘導するときにも用いる考え方であるが,
当時文献[38]を作っているときにも
他研究者からこの連続性不要の考え方に異議が出され驚いたことがあった。
そのため文献[30]にもこの節の内容を発表した。
力学的には非常に明確な考え方だと思うのだが。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
と呼ぶ7.5
- どちらかの呼び名が間違いだということを聞いた記憶があるが,
どちらだったか覚えていない。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
棒としてモデル化できるような寸法を有している8.1
- 船舶も最初は梁として概略設計をすると聞いたことがある。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
と呼ばれ,構造力学の中では最も難しい理論8.2
- 曲面上の微分幾何は,我々の身の回りのEuclid幾何ではなくRiemann幾何で
表現されるため,難しい・・・らしい。
極座標の応力テンソル成分が,下手をすると圧力の次元を持ってないかも
しれないということも想像してみて欲しい。
そうなると構成則もどうするか・・・難しいよね。
事実現場では,シェル理論そのものは知らずに汎用の有限要素解析プログラムを
使っているというのが実態ではないだろうか。
今や,修士修了までにシェルを教える(土木系?)大学・大学院は
ほとんど無いのではないか。
第1著者も航空工学系専攻の授業で「聞いたことがある(呵呵)」だけである。
少なくとも,平板の基礎くらいは身に付けて欲しい。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.