 |
最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
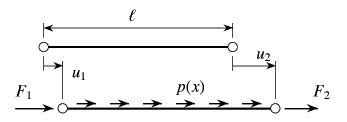
前節の区分的多項式による近似を一般化し,図-5.8の
ような長さ![]() の1有限要素に外力が作用して
図のような変位が生じてつり合ったとして近似方程式を求めてみよう。
この一般的な場合の仮想仕事の式
は
の1有限要素に外力が作用して
図のような変位が生じてつり合ったとして近似方程式を求めてみよう。
この一般的な場合の仮想仕事の式
は
となる。ただし,ここの![]() は1有限要素の長さである。
つまり前節のような区分的多項式による近似の1要素に注目し,
相隣接する要素同士はあとで適切に連続させることにしているだけで,
本質的には前節での定式化との違いは無い。
まず,この1有限要素の変位を多項式で近似することから始めよう。
変断面でも容易に定式化できるが,
簡単のために1有限要素は単一材料でできた等断面部分だとする。
は1有限要素の長さである。
つまり前節のような区分的多項式による近似の1要素に注目し,
相隣接する要素同士はあとで適切に連続させることにしているだけで,
本質的には前節での定式化との違いは無い。
まず,この1有限要素の変位を多項式で近似することから始めよう。
変断面でも容易に定式化できるが,
簡単のために1有限要素は単一材料でできた等断面部分だとする。
式(5.13)で,変形できる物体にとって
最も重要な項は第1項の内力仮想仕事項だから,それが
無くならないためには,![]() の近似関数には1階の微係数が存在する必要がある。
したがって,多項式を用いる限りは`
の近似関数には1階の微係数が存在する必要がある。
したがって,多項式を用いる限りは`![]() 'の1次以上の
高次の多項式が必要となる。また境界条件によっては
柱が剛体的に移動する場合もあるため,平行移動を表す`
'の1次以上の
高次の多項式が必要となる。また境界条件によっては
柱が剛体的に移動する場合もあるため,平行移動を表す`![]() '(定数)も必要である。
さらに幾何学的境界条件からは,
隣接する要素との間で変位
'(定数)も必要である。
さらに幾何学的境界条件からは,
隣接する要素との間で変位![]() が両端で連続する必要があるから,1有限要素には
最低でも自由度が二つ必要になる。
このように考えると,最も次数の低い多項式の選択としては,
二つの自由度
が両端で連続する必要があるから,1有限要素には
最低でも自由度が二つ必要になる。
このように考えると,最も次数の低い多項式の選択としては,
二つの自由度![]() ,
, ![]() を用いて
を用いて
と置くことが可能なようだ。ここでも
やはり,物理的に意味の無い係数![]() を使う代わりに,前節で示したように
両端の変位
を使う代わりに,前節で示したように
両端の変位![]() ,
, ![]() を未知係数とするような表現にしたい。
そうすることによって,幾何学的境界条件を満足させられる近似関数と
対応する重み関数にすることが容易にできそうだ。つまり上式から
を未知係数とするような表現にしたい。
そうすることによって,幾何学的境界条件を満足させられる近似関数と
対応する重み関数にすることが容易にできそうだ。つまり上式から
という関係を得るので,結局![]() ,
,
![]() と
置き換えればよく,式(5.14)は次のように書き改められる。
と
置き換えればよく,式(5.14)は次のように書き改められる。
このような関数![]() は変位を近似するために仮定した
関数なので変位関数
,あるいは一般的には試行関数
とか内挿関数
と5.3呼ばれる。
は変位を近似するために仮定した
関数なので変位関数
,あるいは一般的には試行関数
とか内挿関数
と5.3呼ばれる。
以上を仮想仕事の式(5.13)に代入して整理すると
となる。すなわち各仮想変位![]() と
と![]() 毎にまとめると
毎にまとめると
を満足していればいいことになる。ここに
で定義したものはそれぞれ,等価節点外力
成分および要素剛性行列
要素である。後者は具体的にその積分を実行すると
という値を持つ。したがって
式(![]() )が任意の仮想変位
)が任意の仮想変位![]() と
と![]() に対して
成立するためには,それぞれの係数がいずれも零であればよく
に対して
成立するためには,それぞれの係数がいずれも零であればよく
を得る。この式は,一つの要素の両端節点に作用している力と節点変位の
関係を代数方程式で表したつり合い式であり,要素剛性方程式と
呼ばれる。特にこの式は引張り圧縮のみで抵抗する柱の1要素の剛性方程式である
ため,柱の要素剛性方程式
と呼ばれる。式(5.17) (5.18)から
柱の1有限要素は,バネ定数
![]() の線形バネとして
取り扱えばいいこともわかる。
だから,章-2でトラス部材のことを検討したときに,
簡単のために線形バネに置き換えたのである。
の線形バネとして
取り扱えばいいこともわかる。
だから,章-2でトラス部材のことを検討したときに,
簡単のために線形バネに置き換えたのである。
梁の場合も図-5.9のような
一般的な状態を対象として仮想仕事式
を求めると
となる。ただし![]() は1有限要素長である。
は1有限要素長である。![]() を近似する関数は
を近似する関数は
という条件から,四つの自由度を持つ3次の多項式が最低次の多項式であり
と近似すればよさそうだ。
さらに,この物理的に意味の無い未知係数![]() (
(![]() )を
要素両節点でのたわみとたわみ角に関係付けると,最終的に
)を
要素両節点でのたわみとたわみ角に関係付けると,最終的に
という表現になる。
ここに梁の変位関数は
と定義される。
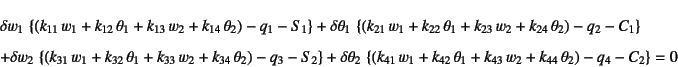
となる。ここに![]() と
と![]() は
は
(5.22)
で定義される剛性行列要素と等価節点外力
成分である。これが任意の![]() ,
,
![]() (
(![]() )に
対して成立する条件から,梁の要素剛性方程式
が
)に
対して成立する条件から,梁の要素剛性方程式
が
と表現できる。
式(5.21)を式(5.22a)に代入すると,
剛性行列![]() が具体的に
が具体的に
と求められる。 なお簡単のためにこの章では,括弧無しの太字で行列を表している。 また,変位関数を図-5.4と同様の区分的多項式として 表したのが図-5.10である。
一つの例として,両端固定の棒に図-5.11のような
等分布外力のみが作用している場合に,端部の反力を
剛性方程式(5.18) (5.23)で計算してみる。
この場合は剛性方程式右辺の両端の変位成分はすべて零になるので,
柱と梁の支点反力はいずれも
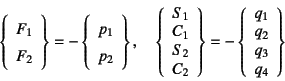
となる。すなわち等価節点外力の符号を換えたものは
それぞれ,分布外力を受ける両端固定の棒の不静定反力であることがわかる。
特に等分布外力である場合の値を計算してみると
という値になる。![]() ,
, ![]() ,
, ![]() ,
, ![]() は分布外力の長さ方向の総和の
半分ずつになっているので直感的な理解も容易である。
また
は分布外力の長さ方向の総和の
半分ずつになっているので直感的な理解も容易である。
また![]() ,
, ![]() は節-4.1.4 (2)で
算定されていた不静定モーメント反力式(4.33)に一致して
おり,1要素剛性方程式から求められる両端の不静定反力も厳密解に
一致していることがわかる。
ただし,このように反力が厳密解に一致するのは,節点変位が
厳密解に一致するのと同様,梁や柱特有の特殊な場合のみに
見られることであり,
一般には近似解しか得ることができないことには十分留意しておく必要がある。
は節-4.1.4 (2)で
算定されていた不静定モーメント反力式(4.33)に一致して
おり,1要素剛性方程式から求められる両端の不静定反力も厳密解に
一致していることがわかる。
ただし,このように反力が厳密解に一致するのは,節点変位が
厳密解に一致するのと同様,梁や柱特有の特殊な場合のみに
見られることであり,
一般には近似解しか得ることができないことには十分留意しておく必要がある。
前節では,対象とする構造系を複数の有限要素に分割し,あとで適切に 連続させることを条件とした上で個々の要素で仮想仕事式が成立する ものとして,1有限要素のつり合い式に対する要素剛性方程式を導いた。 ここでは,その分割した要素同士を適切に連続させる方法と, それを用いて元の境界値問題を解く方法とを説明し,いくつかの例を示す。 実際には,剛性行列や等価節点外力も電子計算機の中で数値的に 計算されれることも多く,以下の手法も数値的に処理されることが多いが, ここではその基礎について梁を対象とした具体例を用いて説明する。
いま図-5.12のように二つの有限要素の共有
節点2に集中外力が作用している場合を考えて,この要素を
連続させて全体剛性方程式を求める方法を説明しよう。図のように
この節点2のすぐ左右をそれぞれ`![]() ', `
', `![]() 'という
節点番号で区別すると,それぞれの要素毎に式(5.23)の
要素剛性方程式が成立するので
'という
節点番号で区別すると,それぞれの要素毎に式(5.23)の
要素剛性方程式が成立するので
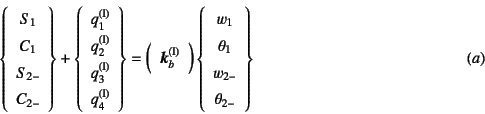
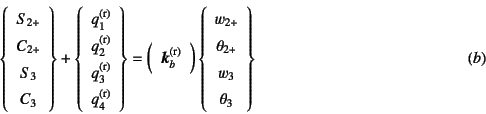
を満足している。ここに上付きの(l) (r)はそれぞれ,節点2のすぐ
左右の要素の値を区別するために用いた記号である。
載荷された部分では図の下に示したように,力とモーメントのつり合いから
を満足するように,左右の要素で外力を分担して抵抗している。一方,
この部分のたわみとたわみ角がもし連続していないと,二つの
要素がここで分離したり折れ曲がったりしてしまう。したがって
変位の連続条件は
でなければならない。
変位の連続条件を考慮しながら式(a)の第3, 4式と
式(b)の第1, 2式とを
上の連続条件式(c)に代入して整理すると
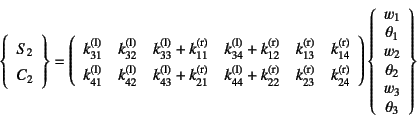
となる。これと式(a)の上2行と,式(b)の下2行の
四つの式とを併せて行列表示すると
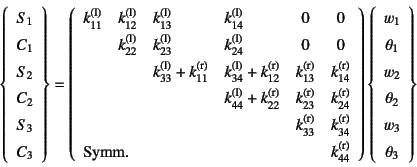
が二つの要素を繋いだ全体剛性方程式になっている。
もう少し見通しがよくなるように次の記号を定義する。
ここに,
![]() (X=A, B, C)は
それぞれ剛性行列
(X=A, B, C)は
それぞれ剛性行列![]() の2
の2![]() 2の小行列である。
これを用いて上の最後の結論を記述すると,二つの要素で全体系を
解こうとする場合の全体剛性方程式は
2の小行列である。
これを用いて上の最後の結論を記述すると,二つの要素で全体系を
解こうとする場合の全体剛性方程式は
となる。すなわち下線部のように,相隣接する要素の共有節点での 各量を加え合わせれば,最終的な全体剛性方程式が求められることが わかる。このように行列を機械的に重ねていく方法を直接剛性法 と呼んでいる。
具体的な使い方を図-5.13の例を用いて説明しよう。
この場合は境界条件から,まず
であり,外力条件は
となる。これを式(5.27)に代入すると,その
第1, 2, 5, 6式は左辺右辺共に未知量を含んでいるのに
対し,第3, 4行目のみは左辺がすべて既知であり,未知量は
右辺にしか存在しないことがわかる。よって後者の2式を
取り出すと
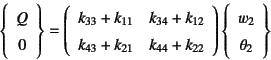
を得る。ここでは左右の要素の剛性と長さが等しいので,
それを区別する上付き記号は省略した。
具体的に値を代入して逆行列を計算すると
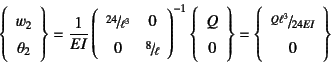
と中央のたわみとたわみ角を求めることができる。
この解を元の全体剛性方程式の第1, 2, 5, 6式に
代入することによって,支点反力が
![]() ,
,
![]() と求められ,たわみ・たわみ角も支点反力・不静定
モーメントも,厳密解(図-4.29付近)の
と求められ,たわみ・たわみ角も支点反力・不静定
モーメントも,厳密解(図-4.29付近)の![]() を
を![]() に
置き換えた答に一致する。
に
置き換えた答に一致する。
もう一つの簡単な例として図-5.14にある
等分布外力を受ける2径間連続梁を解いてみる。
特徴を出すために,長さの違う左右のスパンの曲げ剛性が
異なる値を持つようにした。図では梁の上面を揃えてあるが,
正確には2部材の図心の位置も揃っている5.4ものとする。
式(5.25)で等分布外力の
場合の等価節点外力成分は算定できているので,
式(5.26)を用いてそれぞれの要素の
要素剛性方程式を簡易表示すると
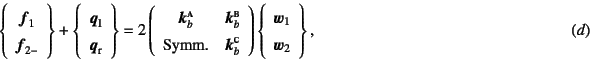

でなければならない。
また境界条件および載荷条件は
で与えられる。
上の三つの要素剛性方程式を用いて直接剛性法を使い,
それに上で示した境界条件および載荷条件を代入すると,
全体剛性方程式が
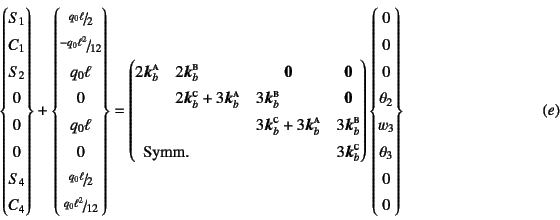
となる。この第4, 5, 6式だけが右辺のみに 未知量を含む式になっており,それを取り出すと
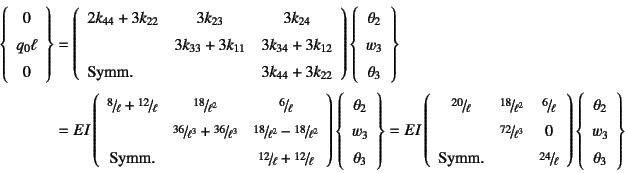
となっている。したがって逆行列を必要な成分だけ計算すると最終的に変位が
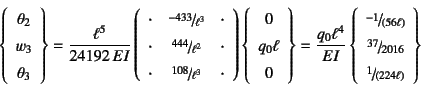
と求められる。これを残りの全体剛性方程式(![]() )に代入すれば,
支点反力と不静定モーメントが
)に代入すれば,
支点反力と不静定モーメントが
と求められる。
求められた節点変位の値を式(5.20)で仮定した
変位関数の係数に代入することによって,各要素の任意点での
変位を関数として得ることができるから,その2階の微係数を算定すれば
各要素毎の曲げモーメント分布も求めることができる。
しかし,変位関数が3次の多項式で近似されていたため,曲げモーメント
分布は線形にしかならず,この例の場合も計算すると
左側のスパンで
となり,右側のスパンも二つの要素のそれぞれの左端を![]() の原点にすれば
の原点にすれば
にしかならない。図-5.15の直線分布が このようにして計算されたモーメント分布であり, 曲線が厳密解を示している。図-5.6の柱の場合には 軸力が最小2乗法 的近似解になっていたが,梁の場合には有限要素法の 曲げモーメントの近似解,つまりたわみの2階の微係数が, 厳密解の最小2乗法的な近似解になっていることがこの図から明らかである。
ところで,有限要素法が近似解法であるにもかかわらず,
柱と梁の場合は,節点で得ることができた変位成分は厳密解に一致していたし,
等分布外力の作用した両端固定梁の不静定反力も厳密解に一致していた。
つまり上で求めたように,式(![]() )の全体剛性方程式からは
支点反力と不静定モーメントの正解が求められていた。
それなら,同じように曲げモーメント図も厳密なものが計算できないだろうか。
そこで今度は要素剛性方程式(
)の全体剛性方程式からは
支点反力と不静定モーメントの正解が求められていた。
それなら,同じように曲げモーメント図も厳密なものが計算できないだろうか。
そこで今度は要素剛性方程式(![]() )に注目すると,この要素剛性方程式の
両端の外力は要素の内力そのもののか,あるいはその符号を替えたものに
一致していることが,その定式化や図-5.12等からわかる。
そこで,求められた変位の解を上述のように全体剛性方程式や変位関数の微係数に代入する代わりに,要素剛性
方程式(
)に注目すると,この要素剛性方程式の
両端の外力は要素の内力そのもののか,あるいはその符号を替えたものに
一致していることが,その定式化や図-5.12等からわかる。
そこで,求められた変位の解を上述のように全体剛性方程式や変位関数の微係数に代入する代わりに,要素剛性
方程式(![]() )に代入してみよう。
そして内力の正の向きと外力の向きとを
考慮しながら,各要素毎に端部の曲げモーメントを要素剛性方程式から
計算すると
)に代入してみよう。
そして内力の正の向きと外力の向きとを
考慮しながら,各要素毎に端部の曲げモーメントを要素剛性方程式から
計算すると
と求められる。実は![]() と
と![]() は上で求めた厳密な不静定曲げモーメントに
一致しており,また
は上で求めた厳密な不静定曲げモーメントに
一致しており,また![]() と
と![]() は中間節点箇所の左右の
内力曲げモーメント(この例では集中外力モーメントが作用していないから
同じ値)になっている。
そして,静定系の曲げモーメント分布が(有限要素法を使うまでもなく)
既知であることから,一旦節点の内力曲げモーメントが得られさえすれば,
簡単に図-5.15の曲線のような
厳密な曲げーモーメント分布図を描くことができるはずだ。
つまり梁の問題では,正しい曲げモーメント図を計算するためにも
有限要素法は有用な手法の一つであると言えよう。
は中間節点箇所の左右の
内力曲げモーメント(この例では集中外力モーメントが作用していないから
同じ値)になっている。
そして,静定系の曲げモーメント分布が(有限要素法を使うまでもなく)
既知であることから,一旦節点の内力曲げモーメントが得られさえすれば,
簡単に図-5.15の曲線のような
厳密な曲げーモーメント分布図を描くことができるはずだ。
つまり梁の問題では,正しい曲げモーメント図を計算するためにも
有限要素法は有用な手法の一つであると言えよう。
このように,有限要素法は近似解法の一つではあるものの, 対象が柱か梁に限定されていれば,節点での変位成分と要素剛性方程式から 求められる内力の値とは厳密解に等しいことを示すことができた。 現在のように有限要素法が一般的な境界値問題の汎用的近似解法と して認識される以前に,節-5.4.1に示すように, 元の境界値問題を厳密に解いて剛性方程式と同じ形式の基礎式を求め, それを用いた解法をマトリックス構造解析法 と呼んで構造力学・構造工学分野では用いていた。 あるいは古典的には節-5.5に示す たわみ角法や三連モーメントの定理として用いていた。 この基礎式と有限要素法の剛性方程式とは完全に一致するか, 単なる項の並べ替えを行ったものになっていることから, 有限要素法で節点での厳密解が求められるのは当然なのである。 有限要素法の発達はこのマトリックス構造解析法を発端としている。 ただ一般論として,有限要素法があくまでも近似解法であることは 心に留めておくべきである。
次の演習問題のようなまっすぐの連続梁を解く有限要素プログラムは 各種存在すると思われるが,著者らが作成したプログラムも電子的に 入手可能になっている。図-5.16のような 等分割要素に対する処理をパーソナルコンピュータ 上で会話型で行えるようになっている。 スパン途中にヒンジやバネ支持も挿入できる。 入手方法についてはまえがきを参照のこと。 できれば各自,プログラミングの練習として少なくとも一直線上の連続梁くらいは 解けるものを作って欲しい。 このような連続梁であれば,直接剛性法をプログラミングすることは そんなに難しいものにはならないからだ。 また,有限要素法を越えて,上で説明したように曲げーモーメントと せん断力の分布図を描くデータも計算するように工夫してみて欲しい。
柱が解けるのなら図-5.18の不静定平面トラスも 有限要素法で解けるだろう。 トラスの1本1本の部材は両端がヒンジで接続されており,部材中間には 外力が作用していないため,曲げモーメントによってではなく 軸の圧縮引張りだけで抵抗している。したがって トラスの各部材を柱要素として取り扱うことができるはずだ。
さて,
図に示したようにトラスの各部材はお互いに異なる方向を向いているため,
単純な柱と違い部材両端にはせん断外力成分も作用させることができる。
しかし上でも述べたように,このせん断外力に対して曲げで
抵抗するとは考えない上に,
部材に分布する外力も考えない。
したがって,図-5.19のように
それぞれの成分を定義したとしても,トラス部材の要素剛性方程式は
柱としての抵抗しか無いので
と書かざるを得ない。つまり,剛性行列の第2, 4行列の要素は零 であり,両端自由の場合にはせん断外力には抵抗できない。
一方それぞれの部材は同じ方向を向いたものではなく, それぞれが任意の方向を向いている。 つまり,このトラス部材の場合の要素剛性方程式(5.28)は それぞれの部材軸方向を要素座標とする系で定義されたものである。 ということは,ある一つの節点での力と変位成分が, 隣り合う部材間では異なる方向の成分として定義されてしまうことになる。 このままでは,複数の有限要素同士の連続条件を考慮するのに,座標系の 違いを考慮して計算する等煩雑な手続きが必要となる。 そこで,すべての要素に共通する全体座標系での成分を各節点の 未知数とするような要素剛性 方程式を誘導しておけば,前節で用いた直接剛性法が,お互いに向きの 異なる要素間に対してもそのまま適用でき便利である。
すなわち,図-5.20の![]() -
-![]() 軸で定義される
要素座標系においては式(5.28)が成立している。
一方,
軸で定義される
要素座標系においては式(5.28)が成立している。
一方,![]() -
-![]() 座標系は空間に固定した座標系で,
すべての要素に共通する全体座標系とする。ということは,
要素剛性方程式(5.28)の両辺の各量を
座標系は空間に固定した座標系で,
すべての要素に共通する全体座標系とする。ということは,
要素剛性方程式(5.28)の両辺の各量を![]() -
-![]() 全体座標系で定義された
量に変換すれば,すべての部材の要素剛性方程式を,一つの共通した
全体座標系における量で表現できることになる。
柱の場合はたまたま,剛性方程式両辺の列行列が
ちょうど2次元ユークリッド空間のベクトル成分と
同じになっているから,この二つの座標の成分間の関係は
全体座標系で定義された
量に変換すれば,すべての部材の要素剛性方程式を,一つの共通した
全体座標系における量で表現できることになる。
柱の場合はたまたま,剛性方程式両辺の列行列が
ちょうど2次元ユークリッド空間のベクトル成分と
同じになっているから,この二つの座標の成分間の関係は
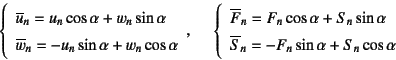
となる![]() 。したがって,座標変換行列を
。したがって,座標変換行列を
と定義しておくと,それぞれのベクトル成分が
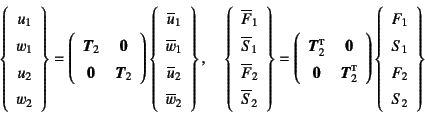
となる。この両式を式(5.28)の両辺に代入して
整理すると,最終的な全体座標系における要素剛性方程式
が
と求められる。
あるいはこの右辺の行列乗算を実行し,座標変換された剛性行列
としてその成分を陽に表すと
となっている。
例として図-5.18の平面トラスを解いてみよう。
部材1-2は長さが
![]() であるが,
要素座標系が全体座標系と一致しているので
であるが,
要素座標系が全体座標系と一致しているので![]() でいい。
一方部材2-3は要素座標系を節点2から3の方向に
とった方が便利なので,全体座標系とのなす
角度は
でいい。
一方部材2-3は要素座標系を節点2から3の方向に
とった方が便利なので,全体座標系とのなす
角度は
![]() あるいは
あるいは![]() になっている。
したがって,それぞれの要素剛性方程式は式(5.31)を
用いて
になっている。
したがって,それぞれの要素剛性方程式は式(5.31)を
用いて

と表現できる。この二式ともに同じ全体座標系で定義されているから
共有節点2に対して直接剛性法を用いることができ,最終的な
全体剛性方程式は
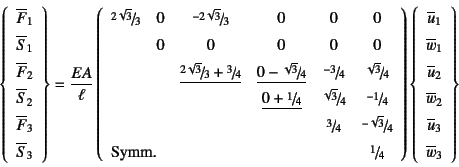
となる。下線部が共有節点2について重ね合わせた部分である。
境界条件は,節点1, 3ですべての変位成分が固定されていること,
節点2に二つの外力が作用していることから
と与えられている。全体剛性方程式のうち,
左辺が与えられている第3, 4行目が先に解けるはずなので
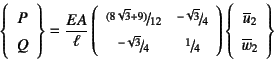
となり,これを節点2の変位成分について解けばいい。その結果
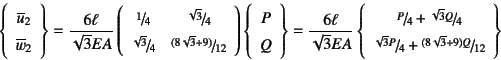
を得る。これを残りの全体剛性方程式の第1, 2, 5, 6行目に代入
すれば,支点反力がそれぞれ
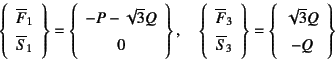
と算定できる。
設計のことを考えると,
最終的にはそれぞれの部材の軸力を計算する必要があるが,これも
連続梁の例と同様,
要素剛性方程式の![]() 方向の両端の節点軸力
方向の両端の節点軸力![]() ,
, ![]() ,
あるいはその符号を替えたもの
,
あるいはその符号を替えたもの![]() ,
, ![]() で算定できる。
あるいは上で得た全体座標系での変位成分を要素剛性方程式に代入して
求められる要素両端外力に,座標変換行列を逆にかけて
要素座標系に戻すことによっても節点軸力を求めることができる。
この例では,要素1-2は
で算定できる。
あるいは上で得た全体座標系での変位成分を要素剛性方程式に代入して
求められる要素両端外力に,座標変換行列を逆にかけて
要素座標系に戻すことによっても節点軸力を求めることができる。
この例では,要素1-2は
![]() となる。
要素2-3では座標変換が必要になり
となる。
要素2-3では座標変換が必要になり
となる。図-5.21に結果を示した。
図-5.22に示したのは,パーソナルコンピュータ
上で作った有限要素プログラム
による連続不静定トラスの解析例で
ある。a〜oの15本の部材が節点1〜9で繋がった
簡単なトラスで,各部材の長さと外力は図示した通りだが,Young率は
すべて200GN/m![]() と共通にした。ただし
断面積は表-5.1の3種類を
用いている。図-5.22の
上図には全体剛性方程式を解いて得た変位を誇張して
示し,下の図には軸力を棒グラフで示した。
また,求められた軸力と支点反力の数値も表-5.2に
列挙してある。負の軸力は圧縮で,上弦材が圧縮を受けている。
反力は
と共通にした。ただし
断面積は表-5.1の3種類を
用いている。図-5.22の
上図には全体剛性方程式を解いて得た変位を誇張して
示し,下の図には軸力を棒グラフで示した。
また,求められた軸力と支点反力の数値も表-5.2に
列挙してある。負の軸力は圧縮で,上弦材が圧縮を受けている。
反力は![]() 方向の外力として示したので,すべて上向きの反力である。
このプログラムもまえがきに書いた方法で入手可能である。
例として図-5.22用のデータファイル等を添付してある。
方向の外力として示したので,すべて上向きの反力である。
このプログラムもまえがきに書いた方法で入手可能である。
例として図-5.22用のデータファイル等を添付してある。
骨組というのは,梁と柱を縦横に並べ,それぞれを剛結して
組み立てた構造系である。
さらに,ある平面内に組み立てられた骨組で,その同じ面内にのみ外力が
作用して,その面内でのみ変形する骨組の問題を平面骨組問題と呼ぶ。
したがって各部材は,軸力の作用と曲げの作用を同時に受けると
考えなければならず,上で誘導した柱および梁の要素剛性方程式を同時に
考慮する必要がある。
そこで図-5.24のような1有限要素を考えることにすると,
式(5.18)の柱の剛性方程式と式(5.23)の梁の
剛性方程式とを一本化して
とすればいいことがわかる。剛性行列の各要素および等価節点外力は 各成分共に既に定義されている。 等価節点外力については,与えられている量であって 演算上は節点の集中外力と同様に取り扱えばいいから,以下,簡単の ために省略する。
骨組の場合も一般には前節の平面トラスと同様,各部材はそれぞれ別々の
方向を向いて配置されている。トラスとの違いは,部材間が
たいていの場合は剛結されている点である。ヒンジが入るような
場合も簡単に定式化できるが,詳細については
文献[118]等を参照のこと。
式(5.32)は図-5.25の![]() -
-![]() 座標系
で成立する要素剛性方程式である。要素座標系と全体座標系の
間の関係の中でトラスに無かったのは曲げモーメントとたわみ角で
あるが,ここで対象としているのは平面問題なのでこの二つに
ついては座標変換の必要が無い。したがって,座標変換行列を
座標系
で成立する要素剛性方程式である。要素座標系と全体座標系の
間の関係の中でトラスに無かったのは曲げモーメントとたわみ角で
あるが,ここで対象としているのは平面問題なのでこの二つに
ついては座標変換の必要が無い。したがって,座標変換行列を
と拡張して定義すると,それぞれの
節点外力および変位の座標変換則は
となる![]() 。
したがって,平面トラスの場合と同様の座標変換の演算を
行うことによって,最終的な全体座標系における要素剛性方程式
が
。
したがって,平面トラスの場合と同様の座標変換の演算を
行うことによって,最終的な全体座標系における要素剛性方程式
が
と表現できる。
ここに,全体座標系での外力ベクトル成分と変位成分を簡単のために
と置いた。![]() は式(5.32)右辺にある骨組の剛性行列
で
は式(5.32)右辺にある骨組の剛性行列
で
と定義した。
最後の式の
![]() (X=A, B, C)は
実線で区分けした3
(X=A, B, C)は
実線で区分けした3![]() 3の小行列である。
この小行列を用いると式(5.35)は
3の小行列である。
この小行列を用いると式(5.35)は
とも表現できる。
図-5.26の例を解いてみよう。
この場合は要素1-2は![]() 傾いた部材であるが,要素2-3は
全体座標系と要素座標系が一致している。したがって,
直接剛性法によって全体剛性方程式を求めると
傾いた部材であるが,要素2-3は
全体座標系と要素座標系が一致している。したがって,
直接剛性法によって全体剛性方程式を求めると
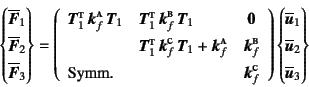
でいい。ここの座標変換行列は
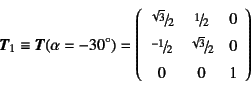
という値を持つ。
境界条件と載荷条件は
と与えられているので,上の全体剛性方程式のうち左辺が既知の第4, 5, 6行目が
先に解くべき式になり
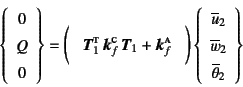
を解けばいいことになる。具体的に剛性行列の要素に値を代入すると
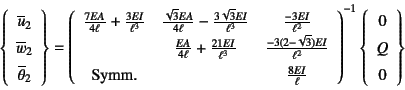
となるから,この逆行列を計算すれば解を得る。 その結果を用いて全体あるいは要素剛性方程式を前節同様 適切に用いると,支点反力や曲げモーメント図・せん断力図・ 軸力図が算定できる。
ここまでの例で見たように,剛性方程式を用いて解く場合にはまず 力学境界条件の与えられている節点での式が解け,すべての節点変位が 先に求められる。よく変位法 と呼ばれる理由はここにある。 ここでは,計算機の中で剛性行列に境界条件・外力条件を 代入して変位を計算する手順について概説しておく。
全体座標系における集中外力ベクトルと分布外力ベクトルが
それぞれ
![]() ,
,
![]() で
表され,直接剛性法によって全体剛性方程式を
で
表され,直接剛性法によって全体剛性方程式を
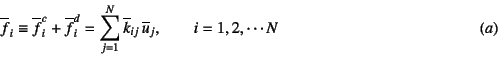
のように得たとする。これに外力条件を代入するのは簡単で,
左辺の
![]() の対応する成分を与えればいい。
次に,幾何学的境界条件が例えば節点
の対応する成分を与えればいい。
次に,幾何学的境界条件が例えば節点![]() で
で
と与えられた場合,これを上の全体剛性方程式(a)に
代入して整理すると
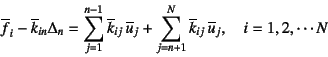
となる。この第![]() 行目のみを式(b)と置き換え,
その他の行はそのままにして行列表示すると
行目のみを式(b)と置き換え,
その他の行はそのままにして行列表示すると
を全体剛性方程式と考えればいいことになる。
第![]() 行目は式(b)そのものである。
このようにして,
与えられた幾何学的境界条件をすべて全体剛性方程式に組み込んでしまえば,
左辺は既知量のみとなり,
正しい組み合わせで幾何学的境界条件が与えられてさえいれば
右辺の剛性行列も正則になって逆行列が存在し,すべての変位成分を
求めることができる。このような手順で全体剛性方程式を解き,
内力を要素剛性方程式から求める場合の代表的な
フローチャートを図-5.27に示した。
また図-5.28(a)は,
数値的に解析した骨組の例である。
この解析プログラム
もまえがきに記した方法で入手可能である。
与えられる境界条件の種類に制限があるが,支点沈下等も取り扱うことが
できるようになっている。
行目は式(b)そのものである。
このようにして,
与えられた幾何学的境界条件をすべて全体剛性方程式に組み込んでしまえば,
左辺は既知量のみとなり,
正しい組み合わせで幾何学的境界条件が与えられてさえいれば
右辺の剛性行列も正則になって逆行列が存在し,すべての変位成分を
求めることができる。このような手順で全体剛性方程式を解き,
内力を要素剛性方程式から求める場合の代表的な
フローチャートを図-5.27に示した。
また図-5.28(a)は,
数値的に解析した骨組の例である。
この解析プログラム
もまえがきに記した方法で入手可能である。
与えられる境界条件の種類に制限があるが,支点沈下等も取り扱うことが
できるようになっている。
節-4.7.1で取り上げた弾性床上の梁についても,
同様の手順で要素剛性方程式を誘導できる。仮想仕事式
が
であることは,梁の場合と同様の演算を式(4.86)に
対して行えば容易に示すことができる。
用いる変位関数は,その条件が初等梁理論と同じであることから
前節で用いた変位関数式(5.20)が使え,
最終的に剛性方程式
が
と求められる。ここに![]() は式(5.24)で
定義されたものと同じであり,上式(5.40)左辺第2項に
関する剛性行列が
は式(5.24)で
定義されたものと同じであり,上式(5.40)左辺第2項に
関する剛性行列が
で定義される。これが,![]() が一様な場合の弾性床抵抗を代表する剛性行列
である。
弾性床上の梁の問題の変位の厳密解に指数関数が存在することは,
式(4.87)で示した通りである。
したがって,区分的多項式で変位を近似した
剛性方程式から求められる有限要素法による近似解は,上の柱や梁の場合とは異なり,
節点位置であっても厳密解には一致しないことに注意すべきである。
解法は普通の梁と同じなので割愛する。
が一様な場合の弾性床抵抗を代表する剛性行列
である。
弾性床上の梁の問題の変位の厳密解に指数関数が存在することは,
式(4.87)で示した通りである。
したがって,区分的多項式で変位を近似した
剛性方程式から求められる有限要素法による近似解は,上の柱や梁の場合とは異なり,
節点位置であっても厳密解には一致しないことに注意すべきである。
解法は普通の梁と同じなので割愛する。
図-5.29には,
弾性床上の単純梁の中央に集中荷重を載せた場合の,
中央のたわみ![]() と曲げモーメントの有限要素解と
要素数
と曲げモーメントの有限要素解と
要素数![]() の関係を示した。
曲げモーメントは,変位関数の2階の微係数で求めた
場合
の関係を示した。
曲げモーメントは,変位関数の2階の微係数で求めた
場合
![]() と,図-5.15で示したのと同様に
要素剛性方程式の反力から求めた場合
と,図-5.15で示したのと同様に
要素剛性方程式の反力から求めた場合
![]() との二つを示した。
縦軸は有限要素解と厳密解の相対誤差
との二つを示した。
縦軸は有限要素解と厳密解の相対誤差
![]() であり,
両軸ともに対数表示である。
要素サイズを小さくする(要素数を増やす)に従って,近似誤差
が急速に零に漸近している。
図中の直角三角形の勾配が
であり,
両軸ともに対数表示である。
要素サイズを小さくする(要素数を増やす)に従って,近似誤差
が急速に零に漸近している。
図中の直角三角形の勾配が![]() であるから,変位関数の微係数で求めた
曲げモーメント
であるから,変位関数の微係数で求めた
曲げモーメント
![]() が
要素分割数の2乗の速度で零に収束していることがわかる。
また,図-5.7, 5.15の場合と同様に,
たわみの高階微係数で求めた断面力の誤差の方がたわみの誤差よりも大きく,
収束の速度も遅い。
ただし,要素剛性方程式から求めた断面力
が
要素分割数の2乗の速度で零に収束していることがわかる。
また,図-5.7, 5.15の場合と同様に,
たわみの高階微係数で求めた断面力の誤差の方がたわみの誤差よりも大きく,
収束の速度も遅い。
ただし,要素剛性方程式から求めた断面力
![]() の誤差と
収束速度は,変位そのものの誤差の傾向とほぼ同様になっているのは興味深い。
の誤差と
収束速度は,変位そのものの誤差の傾向とほぼ同様になっているのは興味深い。
梁の運動方程式は式(4.88)なので,
この初期値境界値問題に対しても静的問題と
同様に弱形式を求めてみると,形式的に式(5.55)のように
なることは容易にわかる(正確な誘導は節-10.4.7を
参照のこと)。
ここで解くべき問題は時間と場所の関数を求めることであるから,
この「動的な仮想仕事式」に対する動的な剛性方程式を
評価するための変位の近似では,式(5.20)を少し変更して
と置いてみればよさそうだ。 ちょうど変数分離で初期値境界値問題を解くのに似ている。 以下,粘性項は無いものとして誘導する。 式(5.43)を式(5.55)に代入して演算すると, 静的な剛性方程式と異なる項は慣性項のみである。 これは
![\begin{eqnarray*}
m \int_0^\ell \ddot{w} \delta w \dint x &=& m \bigl[
\d...
...ta_1 +
\mu_{43} \ddot w_2 + \mu_{44} \ddot \theta_2 \} \bigr]
\end{eqnarray*}](s2img330.gif)
となる。ここに
となる。
ここに![]() は
は
![]() を
を![]() 要素とする質量
行列は,具体的には式(5.42)の
要素とする質量
行列は,具体的には式(5.42)の![]() を
を![]() で置き換えて
で置き換えて
という成分を持ち,![]() は式(5.24)で定義した
梁の曲げに関する剛性行列である。また
は式(5.24)で定義した
梁の曲げに関する剛性行列である。また
と定義した。
式(5.45)は1要素の動的な要素剛性(運動)方程式であり,
境界条件を代入する前なら
形式的に4自由度系の運動方程式と同じ形をしている。
もちろん4質点系のそれ(対角行列)とは異なり,
質量行列は式(5.42)のように非対角項にも非零な値を
持つ4![]() 4の行列になっている。
このような質量行列を整合質量行列
と呼ぶ。梁の動的問題をこの要素剛性方程式を用いて解く場合には,
質量行列についても剛性行列同様の直接剛性法を適用し,
共有節点に関する要素同士を重ね合わせてやればいい。
4の行列になっている。
このような質量行列を整合質量行列
と呼ぶ。梁の動的問題をこの要素剛性方程式を用いて解く場合には,
質量行列についても剛性行列同様の直接剛性法を適用し,
共有節点に関する要素同士を重ね合わせてやればいい。
自由振動の問題を例として解いておこう。この場合には
外力を零にしておいて周期解を探せばいいだけなので
と置けばいい。ここに![]() は未定の振幅列行列である。
これを式(5.45)の要素剛性方程式に代入すると,
形式的には
は未定の振幅列行列である。
これを式(5.45)の要素剛性方程式に代入すると,
形式的には
を満足していればいいことになる。したがって,
有意な![]() が存在するための条件から
が存在するための条件から
でなければならず,この式が固有振動数![]() を
決定する特性方程式になる。
上で「形式的」と書いたのは,簡単のために境界条件等の
処理についての記述を割愛しているからである。
複数の有限要素で解く場合には,直接剛性法でそれぞれの
行列を重ねたあとに境界条件を代入し,そのあとで上の演算を
行う必要がある。処理法の詳細については座屈についての同様の
計算(p.
を
決定する特性方程式になる。
上で「形式的」と書いたのは,簡単のために境界条件等の
処理についての記述を割愛しているからである。
複数の有限要素で解く場合には,直接剛性法でそれぞれの
行列を重ねたあとに境界条件を代入し,そのあとで上の演算を
行う必要がある。処理法の詳細については座屈についての同様の
計算(p.![]() )あるいは節-10.4.7を
参照のこと。
)あるいは節-10.4.7を
参照のこと。
このようにすると,式(5.47)のように,
行列の固有値問題
の固有値として系の固有振動数を計算できる。
両端単純支持梁の固有振動数を,用いる要素数を増やしながら
求めたのが表-5.3である。
ただし,表で用いた
は,第![]() 次振動数の厳密解と近似解の比である。
要素数が増えるにつれて
解の精度が上がっていくことが明らかである。
工学的に最も重要な最低次の固有振動数は,1要素(2自由度)であっても
わずか11%程度の誤差しか含んでおらず,2要素(4自由度)で
は1%未満になっていることは興味深い。
振動数の近似解が厳密解より大きくなるのは,近似することによって
モデルの変形が真の変形より拘束されたものになってその剛性が大きく
なってしまうからである。
次振動数の厳密解と近似解の比である。
要素数が増えるにつれて
解の精度が上がっていくことが明らかである。
工学的に最も重要な最低次の固有振動数は,1要素(2自由度)であっても
わずか11%程度の誤差しか含んでおらず,2要素(4自由度)で
は1%未満になっていることは興味深い。
振動数の近似解が厳密解より大きくなるのは,近似することによって
モデルの変形が真の変形より拘束されたものになってその剛性が大きく
なってしまうからである。
より複雑な系の場合には,上の整合質量行列の代わりにそれぞれの節点に 何らかの集中質量を配置した集中質量行列 を算定して用いることが,特に自由振動解析において行われることがある。 これについても別途参考文献を参照のこと。 また,自由振動問題ではなく強制振動問題の時刻歴応答解を求める場合には, 式(5.45)を時々刻々解いていかなければならず, 時間微分の項をある時間刻みで差分表示のような漸化式に置き換えて 数値計算することになる。数値解析上の安定性や精度等の問題点や, 具体的な解法等については節-10.4.7や 参考文献[8]等を参照のこと。