最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。

• 4.2.1 集中外力の作用と連続条件
• 4.2.2 集中せん断力の作用
  • 4.2.2.0.1 標準的な解法:
  • 4.2.2.0.2 せん断力図と曲げモーメント図の眺め方:
  • 4.2.2.0.3 静定梁の場合:
  • 4.2.2.0.4 左右対称な系の場合:
  • 4.2.2.0.5 連続梁:
  
  
• 4.2.3 集中モーメントの作用
  • 4.2.3.0.1 標準的な解法:
  • 4.2.3.0.2 静定系の場合:

4.2 集中せん断力や集中モーメントの作用

4.2.1 集中外力の作用と連続条件

ここまでは1径間の梁に分布外力や端外力が与えられた系を対象として， 静定・不静定を問わず一般的な梁の解法の基礎と特徴を説明してきた。 しかし，部材の中間が支えられていたり，中間に集中外力が作用している場合には， その中間位置で何らかの連続条件を与えなければならない。 ちなみに集中外力モーメントというのはわかり難いかもしれない。 例えばいかだのように井桁に組んだ梁（立体骨組）に任意のせん断外力を 載せると，直角に交わっている梁同士は，作用反作用でお互いに ねじりモーメント力も伝達することになる。 このとき，片方の梁にとってのねじりモーメント力は， もう一方の梁にとっては見かけ上の曲げ外力モーメントになる。 つまり， 片方の梁の曲げモーメントが接合点ではもう一方の梁のねじりモーメントに 伝達されている。 このような作用をモデル化したのが集中モーメントである。

さてここでは，その中間位置を 端部境界と同じように考えて，図-4.25のような厚さ零の 部分が支持されるか，あるいはそこに集中的に外力が作用しているものと捉えて， 連続条件を求める。 この厚さ零の部分の両面はそれぞれ梁の断面であり， そこには断面力が図示した方向を正にして発生している。 梁はここで離れたり重なったり，あるいは折れ曲がったりは しないであろうから，最低限変位成分は連続している必要がある。 境界条件の幾何学的境界条件の成分と対応させて 考えると，その連続条件は

(4.44)

となることは容易に理解できるだろう。ここに$a-$, $a+$というのは 点$x=a$の直前直後の座標値^4.7を意味している。 一方力の不連続条件については， 図の厚さ零の部分の内力と外力のつり合いを 考えれば得ることができ，それは

(4.45)

となることも容易に理解できるだろう。

図 4.25: 集中外力が作用する点の（不）連続条件

もしこの中間点がさらに，連続した梁の中間支点上である場合には，もちろん その支点反力に相当する$Q$は未知であるから， 上の式(4.45b)を条件として用いることはできない。 逆にこの式はその中間支点での支点反力を求めるための式になる。 これでは条件が足りなくなるので式(4.45b)に 代わる条件が必要になるが，それはその支点が沈下しないという条件である。 式(4.44b)はたわみが連続であればいいだけの条件 であるから，これにさらにその支点が沈下しない条件を加える必要がある。 つまり，この条件は

$$w(a-)=0, \quad w(a+)=0$$ (4.46)

という二つの条件として認識されなければならない。 これで数の上でも必要な連続条件がすべて揃ったことになる。 このような連続条件をも含めて， 代表的な境界条件をp. の表-4.1に示しておいた。 表では，中間点で支点沈下等が存在する場合に一般化してまとめてある。

4.2.2 集中せん断力の作用

図 4.26: 集中せん断力が中央に作用した不静定梁

4.2.2.0.1 標準的な解法:

最初に，図-4.26にある不静定梁の中央に 集中せん断力が作用している場合を考える。 境界条件は

$$w(0)=0, \quad w'(0)=0, \quad w(\ell)=0, \quad w''(\ell)=0$$

である。載荷点を除いた部分には分布外力が存在していない から $0<x<\slfrac{\ell}{2}$, $\slfrac{\ell}{2}<x<\ell$の それぞれの部分のたわみの一般解は

(4.47)

と表すことができる。これを上の境界条件に代入すると

$$c=0, \quad d=0, \quad \bar{b}=-3\bar{a}\ell, \quad \bar{d}=2\bar{a}\ell^3-\bar{c}\ell$$

となり，中間的な結果として

(4.48)

を得る。まだ$a$, $b$, $\bar{a}$, $\bar{c}$が未定であり， これを $x=\slfrac{\ell}{2}$での 連続条件式(4.44) (4.45)で 決定しなければならない。 まず，たわみとたわみ角は連続しなければ ならないから，それぞれ

$$\ell^3a+2\ell^2b=11\ell^3\bar{a}-4\ell\bar{c}, \qquad 3\ell^2a+4\ell b=-9\ell^2\bar{a}+4\bar{c}$$

となる。 $x=\slfrac{\ell}{2}$での不連続条件式(4.45b) (4.45c)より

$$-6EI a-(-6EI\bar{a})=Q \to \bar{a}-a=\slfrac{Q}{(6EI)}, \qquad 3\ell a+2b=-3\ell\bar{a}$$

と求められる。

以上のように，四つの未知積分定数に対する四つの連続条件が

$$\left(\begin{array}{cccc} 1 & -1 & 0 & 0 \\ -11\ell^3 & \... ...n{array}{c} \slfrac{Q}{(6EI)} 0 0 0 \end{array}\right\}$$

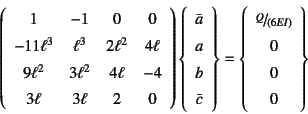
と表現できるので，この係数行列の逆行列で必要な1列目だけを計算すると

$$\left\{\begin{array}{c} \bar{a} a b \bar{c} \end{array... ...slfrac{-3\ell}{32} \slfrac{-\ell^2}{8} \end{array}\right\}$$

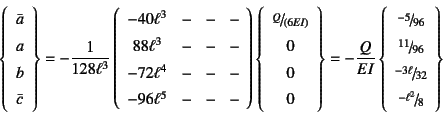
と積分定数が決まる。

したがって $0<x<\slfrac{\ell}{2}$のたわみは

$$w(x)=\dfrac{Qx^2}{96EI}\left(9\ell-11x\right)$$

であり， $\slfrac{\ell}{2}<x<\ell$のたわみは

$$w(x)=\dfrac{5Q}{96EI}(x-\ell)\left\{(x-\ell)^2-3\ell^2\right\}+ \dfrac{Q\ell^2}{8EI}(x-\ell)$$

となる。 もし左端からの$x$座標に対する右端からの独立変数を

$$\xi\equiv\ell-x$$ (4.49)

で定義すると， $\slfrac{\ell}{2}<x<\ell$のたわみは

$$w(\xi)=\dfrac{Q\xi}{96EI}\left(3\ell^2-5\xi^2\right)$$

とも表現できる。それぞれの微係数を計算すれば 曲げモーメントとせん断力の分布も求めることができる。 分布外力が無いから曲げモーメント図は連続した折れ線になり， せん断力図は不連続な定数分布を示すはずである。 結果を図-4.27に示した。

図 4.27: 集中せん断力が作用した左端固定右端単純支持の梁

4.2.2.0.2 せん断力図と曲げモーメント図の眺め方:

ところで，断面力図を直感的に描くときの助けになるように， この図-4.27を使って，断面力図の見方を書いておこう。 まずせん断力図を見ると，スパン中央で上から下方向に$Q$だけの 不連続がある。 ここはちょうど$Q$のせん断力が下向きに作用しているからこうなっているのである。 図の向きと力の向きがよく合っている。 それを踏まえれば，左端では上向きに $\slfrac{11Q}{16}$の不連続が， 右端でも上向きに $\slfrac{5Q}{16}$の不連続があることから， 支点反力が上向きの力として発生したことがわかる。 ただしこの文書では，境界条件式(4.28b)のせん断反力は 下向きを正として定義されていたことから

$$S_1=-\dfrac{11Q}{16}, \quad S_2=-\dfrac{5Q}{16}$$

となる。 一方，曲げモーメント図は負を上向きに描いていたが，それは引張り側を 実際の梁の配置と揃えるためなのだ。 例えば鉄筋コンクリート（引張りに弱いコンクリートを鉄筋で 補強する）でこの図の梁を作ろうとすると， 中央では曲げモーメントが下側に分布していることから， 鉄筋を梁の下方に配置すればいいことがわかる。 これに対し，左端付近では負の曲げモーメントが生じ， 図では上側に分布していることから，鉄筋は上方に配置することになる。 さて境界条件式(4.28c)の外力モーメントの正の向きに 注意すると，左端の反力モーメントは

$$C_1=\dfrac{3Q\ell}{16}$$

となる。

図 4.28: 中央に集中せん断力の作用した単純梁

4.2.2.0.3 静定梁の場合:

次の 例題は基本的な単純梁（4.28）である。 境界条件は両端で

$$w=0, \quad w''=0$$

と与えられる。 この系は静定構造なのでつり合いから曲げモーメント分布を 容易に求めることができるので，4階の 微分方程式から解き始める必要は無い。曲げモーメント分布は

$$M(x)=\left\{\begin{array}{ll} \slfrac{Px}{2}, & 0<x<\slfrac... ...c{P(\ell-x)}{2}, & \slfrac{\ell}{2}<x<\ell \end{array} \right.$$

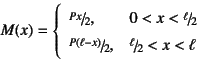
と求められているから，これを式(4.13b)に 代入して積分すればいい。つまり

$$w(x)=\slfrac{-Q}{EI}\left(\slfrac{x^3}{12}+ax+b\right) \quad... ...a}x+\bar{b}\right) \quad \left(\slfrac{\ell}{2}<x<\ell\right)$$

がその一般解となる。境界条件のうち，両端で曲げモーメントが零になる 力学的境界条件$w''=0$は曲げモーメント分布が既に満足しているので， 残る左右端での$w=0$の幾何学的境界条件に上の一般解を代入すると

$$b=0, \quad \bar{b}=-\ell\bar{a}-\slfrac{\ell^3}{6}$$

を得る。したがって，載荷点 $x=\slfrac{\ell}{2}$での たわみとたわみ角の連続条件から$a$と$\bar{a}$を求めればいい。 これはそれぞれ

$$a+\bar{a}=\slfrac{-\ell^2}{4}, \quad a-\bar{a}=\slfrac{\ell^2}{8}$$

となることから， $a=\slfrac{-\ell^2}{16}$, $\bar{a}=\slfrac{-3\ell^2}{16}$となる。 よって $0<x<\slfrac{\ell}{2}$のたわみは

$$w(x)=\dfrac{Qx}{48EI}\left(3\ell^2-4x^2\right)$$ (4.50)

であり， $\slfrac{\ell}{2}<x<\ell$のたわみは 式(4.49)の$\xi$を用いると

$$w(\xi)=\dfrac{Q\xi}{48EI}\left(3\ell^2-4\xi^2\right)$$

と表現できる。左右対称の系であるので，解も左右対称になっているのは 当然である。

4.2.2.0.4 左右対称な系の場合:

図 4.29: 集中せん断力が中央に作用した両端固定梁

もう一つの 例は，図-4.29のような 両端固定梁の場合である。 この場合も左右対称の系であることから 解析するのも左半分だけでよく，その場合の境界条件が

$$w(0)=0, \quad w'(0)=0, \quad w'(\slfrac{\ell}{2})=0, \quad -EIw'''(\slfrac{\ell}{2})=\slfrac{Q}{2}$$

となることも容易に推測できよう。 一般解は3次の多項式で，式(4.47a)と 同じ表現になる。

図 4.30: 中央に集中せん断力を受ける両端固定梁の曲げモーメント分布

これを上の境界条件に代入すると

$$c=0, \quad d=0, \quad a=\slfrac{-Q}{(12EI)}, \quad b=\slfrac{Q\ell}{(16EI)}$$

を得る。したがって左半分の領域のたわみは

$$w(x)=\dfrac{Qx^2}{48EI}\left(3\ell-4x\right)$$

となり，曲げモーメントを求めると

$$M(x)=-EIw''(x)=\dfrac{Q}{8}\left(4x-\ell\right)$$

と線形分布を示す。モーメント図のみを図-4.30に示した。 これより両端の反力モーメントは

$$C_1=\dfrac{Q\ell}{8}, \quad C_2=-\dfrac{Q\ell}{8}$$

となる。

4.2.2.0.5 連続梁:

図 4.31: 連続梁の例

最後に図-4.31の ような2径間連続梁について解析を試みておこう。 この場合の$x=0$, $x=2\ell$での境界条件は共に

$$w=0, \quad w''=0$$

でいい。中央の連続支承部での連続条件が

$$w(\ell-)=0, \quad w(\ell+)=0, \quad w'(\ell-)=w'(\ell+), \quad w''(\ell-)=w''(\ell+)$$

であり， $x=\slfrac{3\ell}{4}$点での連続条件は

$$w(-)=w(+), \qquad w'(-)=w'(+),\qquad w''(-)=w''(+), \qquad \{-EIw'''(-)\}-\{-EIw'''(+)\}=Q$$

でなければならないから合計12個の条件が存在する。

境界条件および連続条件が与えられる点で区分け された三つのそれぞれの区間の一般解は，まず$0<x<\ell$では 等分布外力があることから

$$w(x)=a_1x^3+b_1x^2+c_1x+d_1+\slfrac{q_0x^4}{(24EI)}$$

となり，右スパンの中を境にした左右半分ずつの領域では

$$w(x) = a_2x^3+b_2x^2+c_2x+d_2 \quad \left(\ell<x<\slfrac{3\e... ...3+b_3x^2+c_3x+d_3 \quad \left(\slfrac{3\ell}{2}<x<2\ell\right)$$

と表される。12個の未定積分定数を上に示した12の条件式から求めれば， すべての領域の変位を決定できる。その2階の微係数から 曲げモーメント分布も求めることができる。 とても現実的な解法とは思えないが，力任せに解こうと 思えば解ける正攻法である。 連続梁の解法については節-4.3で 用いる重ね合わせの原理を利用した方が簡単である。 ただし，前述の断面力図の眺め方が理解できているかどうか， 計算せずにせん断力図と曲げモーメント図を描いてみて欲しい。 描いたあとで図-4.44と比べること。 そして時間があれば，一度でいいから自分で解いて， この正攻法がいかに手間がかかるか，そしてどこにも 力学が要らないことについても実感しておいて欲しい。 そうすれば，後述の重ね合わせの原理や有限要素法による 近似解法等の利用のありがたみをさらに感じることができると思う。 また重ね合わせの原理の利用では，変形できる物体の抵抗の 様子を力学的に洞察する力も必要になるので， この正攻法よりは頭の訓練にはなる。 余談ではあるが，大学院入試の構造力学の問題では， こんな微分方程式を用いて解く手法に適した問題は出されないと 考えた方がいいのではないだろうか。というのも，その試験は 力学的センスを確かめるために実施しているのだから。閑話休題。

図 4.32: 中間連続条件の演習問題

1. 図-4.32の(a)に 示したように，不静定梁の 左半分のみに等分布外力が作用している。中央点には零の大きさの 集中外力が作用していると考えればいいから， 式(4.44) (4.45)の連続条件を用いて この系のたわみを求めよ。
2. 図-4.32の(b)に示したように， 中間がバネ定数$k$の線形バネで支持されている場合の 連続条件を求め，この系のたわみや曲げモーメントを求めよ。

4.2.3 集中モーメントの作用

4.2.3.0.1 標準的な解法:

図 4.33: 中央に集中モーメントが作用した両端固定梁

図-4.33のように， 両端固定の梁の中央に 集中モーメントが作用している場合を対象とする。 境界条件は両端で

$$w=0, \quad w'=0$$

である。載荷点を境とする左右の領域で同じく3次の 多項式で一般解が表されるが，左の領域の場合には，左端の 境界条件を代入した式(4.48a)が その一般解になる。また構造形態が左右対称である（外力条件は 対称ではない）ことから，式(4.49)で定義した 右端からの独立変数を用いると，右半分の一般解も 同じ表現になる。したがって，変位の一般解は

$$w(x) = ax^3+bx^2 \quad \left(0<x<\slfrac{\ell}{2}\right), \q... ...}\xi^3+\bar{b}\xi^2 \quad \left(\slfrac{\ell}{2}<x<\ell\right)$$

となる。

図 4.34: 集中モーメントが作用した両端固定梁

ここで

$$( )'=-\D*{}{\xi}, \quad ( )''=\D*[2]{}{\xi}, \quad ( )'''=-\D*[3]{}{\xi}$$

であることに注意して載荷点での連続条件を書き表すと， たわみとたわみ角の連続性から

$$\ell^3a+2\ell^2b=\ell^3\bar{a}+2\ell^2\bar{b}, \quad 3\ell^2a+4\ell b=-3\ell^2\bar{a}-4\ell\bar{b}$$

という条件を得る。曲げモーメントの不連続と せん断力の連続条件は

$$\begin{eqnarray*} -EI(3\ell a+2b)-\{-EI(3\ell\bar{a}+2\bar{b})\}&=&C_0 \\ -EI(6a)-\{-EI(-6\bar{a})\}&=&0 \end{eqnarray*}$$

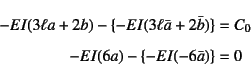
と表される。この4式から未定積分定数が

$$a=-\bar{a}=\slfrac{-2C_0}{(8\ell EI)}, \quad b=-\bar{b}=\slfrac{C_0}{(8EI)}$$

となる。したがって，たわみが

$$w(x) = \dfrac{C_0}{8EI\ell}\left(-2x^3+\ell x^2\right) \quad... ...+\ell \xi^2\right) \quad \left(\slfrac{\ell}{2}<x<\ell\right)$$

と反対称形になる。これを微分すれば曲げモーメントとせん断力の 分布および支点反力を求めることができる。 結果を図-4.34に示した。

4.2.3.0.2 静定系の場合:

図 4.35: 集中モーメントが中央に作用した静定梁

静定の 場合には，これまでの例と同様，曲げモーメント分布を 元にたわみを求めればいいから，2階の微分方程式を 解けばいい。図-4.35の場合には 力のつり合いから曲げモーメントが

$$M(x)=\left\{ \begin{array}{ll} \slfrac{C_0x}{\ell}, & 0<x<\... ...0(x-\ell)}{\ell}, & \slfrac{\ell}{2}<x<\ell \end{array}\right.$$

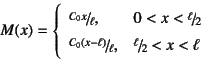
となっている。幾何学的な境界条件は両端で$w=0$である。 上の曲げモーメント分布をそれぞれの区間で積分することに よって，一般解が

$$w(x) = \slfrac{-C_0}{\ell EI}\left( \slfrac{x^3}{6}+ax+b\rig... ...a}x+\bar{b}\right) \quad \left(\slfrac{\ell}{2}<x<\ell\right)$$

と表現できる。第1式を$x=0$の境界条件に，第2式を右端$x=\ell$の 境界条件に代入すると

$$b=0, \quad \bar{b}=-\ell\bar{a}+\slfrac{\ell^3}{3}$$

となる。さらに載荷点でのたわみとたわみ角の連続条件に 代入すると，それぞれが

$$a-\bar{a}=\slfrac{-\ell^2}{2}, \quad a+\bar{a}=\slfrac{5\ell^2}{12}$$

であることから $a=\slfrac{-\ell^2}{24}$, $\bar{a}=\slfrac{11\ell^2}{24}$が求められる。 したがって，たわみが

$$\begin{eqnarray*} w(x)&=&\dfrac{C_0x}{(24\ell EI)}\left(\ell^2-4x^2\right) \quad... ...\ell^2-4\xi^2\right) \quad \left(\slfrac{\ell}{2}<x<\ell\right) \end{eqnarray*}$$

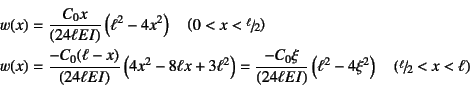
と，これも反対称形になる。図-4.36には たわみ形状を示した。

図 4.36: 集中モーメントが中央に作用した静定梁のたわみ
図 4.37: 不静定梁に集中モーメント
図 4.38: 右スパンはたわまない

1. 図-4.37の梁のたわみを求めて 曲げモーメント図を描け。
2. 図-4.38の連続梁の右スパンが たわまなかった。載荷位置$x$を求めよ。

最新版を正確に読むためには pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。