 |
最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
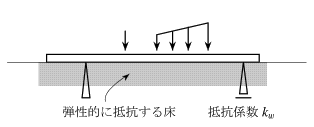
杭や管等のように地中に埋められた棒の曲げや,図-4.78の
ように直接地表に置かれた棒の曲げ挙動をモデル化したものの代表として,
弾性床上の梁理論がある。
最も実用的で代表的な弾性床はWinkler型
と呼ばれるもので,
梁のたわみに比例した弾性抵抗反力を発生する床である。
つまり土圧や
地盤反力のようなものに相当する。
この床の単位長さ当たりの抵抗係数を![]() としたとき,
梁に対しては
としたとき,
梁に対しては
![]() だけの分布反力が変位と逆向きに
作用すると考えるモデルである。したがって,そのつり合い式
は式(4.27b)が
だけの分布反力が変位と逆向きに
作用すると考えるモデルである。したがって,そのつり合い式
は式(4.27b)が
となるだけで,他はすべて通常の梁理論と同じである。 ただ注意しなければならないのは,この床と梁とは接着剤で 接合されており,通常は梁が床から離れることが無いものとしている。
一般解を求めるために![]() として
として
![]() を
上式に代入すると
を
上式に代入すると
と特性方程式を得るから,特性根は
となる。定数![]() 〜
〜![]() を境界条件で決めれば与えられた境界値問題が
解ける。
を境界条件で決めれば与えられた境界値問題が
解ける。
例えば非常に長い杭等のモデルとして,図-4.79に
あるような![]() 軸の正方向に非常に長い梁を考え,その端部に
集中せん断力
軸の正方向に非常に長い梁を考え,その端部に
集中せん断力![]() が作用している場合を解いてみる。
この場合の境界条件は
が作用している場合を解いてみる。
この場合の境界条件は
で与えられる。したがって式(4.87)の一般解の
うちの第1項は![]() での
境界条件を満足し得ないため除外される。
残った積分定数
での
境界条件を満足し得ないため除外される。
残った積分定数![]() ,
, ![]() を
を![]() での境界条件で決定すれば,結局
での境界条件で決定すれば,結局
が解となる。
動的問題の支配方程式はNewtonの法則を用いれば簡単に誘導できる。
例えば柱の場合,式(4.27a)が![]() 方向の
力の総和がつり合っていて物体が静止していることを示している。
これはNewtonの運動方程式で加速度が零の静止している状態である。
動的問題の場合,この(力の総和)が(質量
方向の
力の総和がつり合っていて物体が静止していることを示している。
これはNewtonの運動方程式で加速度が零の静止している状態である。
動的問題の場合,この(力の総和)が(質量![]() 加速度)
に等しくなるというのがNewtonの法則だから,梁の単位長さ当たりの
質量を
加速度)
に等しくなるというのがNewtonの法則だから,梁の単位長さ当たりの
質量を![]() とするとその運動方程式は
とするとその運動方程式は
となる。上付きドット![]() は時間に関する
微係数を表す。分布外力
は時間に関する
微係数を表す。分布外力![]() が無い場合にはこの式は
が無い場合にはこの式は
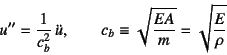
と表現できる。
![]() は密度である。
この式は式(3.99)と同じ形の波動方程式
である。式中の
は密度である。
この式は式(3.99)と同じ形の波動方程式
である。式中の![]() は棒の縦振動
が伝わる波の速度であり,鋼では
は棒の縦振動
が伝わる波の速度であり,鋼では![]() GN/m
GN/m![]() ,
,
![]() kg/m
kg/m![]() から
から![]() km/s程度になる。
この偏微分方程式は
km/s程度になる。
この偏微分方程式は
といった変数変換をすると
という形にできることから,その解は
の形になる。これをd'Alembertの解
と呼ぶ。この式は物理的には,任意時刻に任意の場所で起こっている
事象は,![]() の正方向に速度
の正方向に速度![]() で伝播する
事象
で伝播する
事象![]() と,
と,![]() の負の方向に速度
の負の方向に速度![]() で
伝播する事象
で
伝播する事象![]() との重ね合わせであることを
示している。
詳細は章-11を参照のこと。
との重ね合わせであることを
示している。
詳細は章-11を参照のこと。
同様に梁の曲げ振動
の場合は式(4.27b)
を用いればよく
となることは容易に理解できよう。式(4.13b)が,
曲げモーメントという抵抗力が軸の曲率の
抵抗係数![]() 倍として発生していることを示しているので,
もし材料そのものに粘性が存在して何らかの速度依存の
抵抗力も有していると考えるならば,一つの代表的なモデルと
してはこの式(4.13b)を粘弾性
に拡張した
倍として発生していることを示しているので,
もし材料そのものに粘性が存在して何らかの速度依存の
抵抗力も有していると考えるならば,一つの代表的なモデルと
してはこの式(4.13b)を粘弾性
に拡張した
のような構成則を有していると設定してもよさそうである。
ここに![]() は粘性に関する材料定数である。
このような材料でできた梁の動的問題の場合の
運動方程式は,上式(
は粘性に関する材料定数である。
このような材料でできた梁の動的問題の場合の
運動方程式は,上式(![]() )の代わりに
)の代わりに
とも表現できる。
各量が場所![]() と時間
と時間![]() の
関数になることだけを変更すれば,境界条件等は静的問題のそれと
すべて同じである。
しかし動的問題の場合は時間的な変化を追跡する問題であるから,
この境界条件に加えて初期条件
というものが必要になる。
つまり,ある基準となる時刻(通常は時刻
の
関数になることだけを変更すれば,境界条件等は静的問題のそれと
すべて同じである。
しかし動的問題の場合は時間的な変化を追跡する問題であるから,
この境界条件に加えて初期条件
というものが必要になる。
つまり,ある基準となる時刻(通常は時刻![]() とすることが多い)に
状態がどのようになっているのか規定する必要がある。
このように,境界条件のみならず初期条件をも規定した上で
時間と場所の関数の偏微分方程式を解く問題を初期値境界値問題
と呼んでいる。時間に関しては上の運動方程式からも明らかなように2階の
微係数が最も支配的な項であることから,初期条件も二つ必要になる。
上の梁の曲げの問題の場合には,通常
とすることが多い)に
状態がどのようになっているのか規定する必要がある。
このように,境界条件のみならず初期条件をも規定した上で
時間と場所の関数の偏微分方程式を解く問題を初期値境界値問題
と呼んでいる。時間に関しては上の運動方程式からも明らかなように2階の
微係数が最も支配的な項であることから,初期条件も二つ必要になる。
上の梁の曲げの問題の場合には,通常
として与えることが多い。
一つだけ解法を示しておこう。
一般論は章-10を参照のこと。
例えば両端単純支持に分布外力![]() が作用したときの
振動を,粘性の影響が無いモデルで解いてみる。
解くべき式は
が作用したときの
振動を,粘性の影響が無いモデルで解いてみる。
解くべき式は
であり,境界条件は両端で
となっており,初期条件は式(4.89)で与えられている ものとする。
まず
![]() の
斉次の場合を解いておく必要がある。そこで
の
斉次の場合を解いておく必要がある。そこで![]() を変数分離して
を変数分離して
と表現できるとして,運動方程式に代入して整理すると
となり,左辺は時間![]() のみの関数,右辺は場所
のみの関数,右辺は場所![]() のみの関数と
なる。これが任意時刻の任意の場所で成立するためには,
この両辺共にある定数
のみの関数と
なる。これが任意時刻の任意の場所で成立するためには,
この両辺共にある定数![]() でなければならない。
したがって,
でなければならない。
したがって,![]() は
は
を満足しなければならず,境界条件も![]() ,
, ![]() で
で
となる。
もし![]() の場合に
の場合に
![]() とすると,
この微分方程式の一般解
とすると,
この微分方程式の一般解![]() は
は
であるが,上の境界条件を満足する![]() 〜
〜![]() はすべて零になる。
また,
はすべて零になる。
また,![]() の場合も一般解が
の場合も一般解が
となるものの,やはり境界条件を満足する積分定数はすべて零になる。
もし![]() の場合には,
の場合には,
![]() と
定義しておくと一般解は
と
定義しておくと一般解は
となる。これを境界条件に代入すると![]() で,かつ
で,かつ
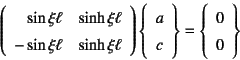
を満足しなければならない。これも![]() であれば成立するが,
もし
であれば成立するが,
もし![]() も
も![]() も零にならない可能性は無いだろうか。
そのためには係数行列が特異であれば
よく,その行列式を零とすることによって
も零にならない可能性は無いだろうか。
そのためには係数行列が特異であれば
よく,その行列式を零とすることによって
であればいい。![]() なので,結局
なので,結局
となる。その結果,固有関数が
と求められる。式(![]() ) (
) (![]() )は
)は![]() に関する固有値
問題を形成しており,
に関する固有値
問題を形成しており,![]() は元の
初期値境界値問題の固有関数列(物理的には振動モード)
と呼ばれ,
は元の
初期値境界値問題の固有関数列(物理的には振動モード)
と呼ばれ,![]() は固有値と呼ばれている。いずれも無限個ある。
は固有値と呼ばれている。いずれも無限個ある。
さて
元の問題に戻って![]() の場合の解を求めてみよう。
そのために,上の固有関数を用いて解が
の場合の解を求めてみよう。
そのために,上の固有関数を用いて解が
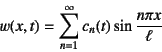
で級数表示できるとする。これを元の運動方程式に代入すると
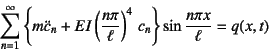
と表現できる。ところで,
このsine関数は面白い性質を持っており
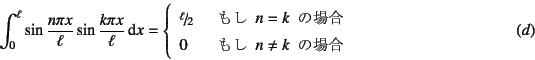
という関係を満足する。これを関数の直交性
と呼ぶ。したがって上式の両辺に
という演算をしてみると,
左辺の級数は実は![]() の場合の1項のみしか残らず,
他はすべて零になる。よって個々の
の場合の1項のみしか残らず,
他はすべて零になる。よって個々の![]() に対して
独立した常微分方程式が
に対して
独立した常微分方程式が
と表現できる。ここに
と置いた。
一方,上の級数表示の解を初期条件に代入すると

となるから,これにも両辺に
という演算をすると,結局上記の直交性から,個々の![]() に関する
独立した初期条件を得
に関する
独立した初期条件を得
となる。![]() に関する微分方程式(
に関する微分方程式(![]() )の一般解は
)の一般解は
となる。この積分定数![]() ,
, ![]() を式(
を式(![]() )の
初期条件で決定すれば
)の
初期条件で決定すれば![]() を求めることができ,
元の問題の解も求めることができる。
このような手法を固有関数による解法と呼ぶが,特に
ここで用いた固有関数のように式(
を求めることができ,
元の問題の解も求めることができる。
このような手法を固有関数による解法と呼ぶが,特に
ここで用いた固有関数のように式(![]() )を満足する
ようなものを直交する固有関数
と呼ぶ。結果論的には上の解法はいわゆるFourier級数
を用いた解法とみなせるが,
天下り的にFourier sine級数になるのではなく,
元の境界値問題に対応する固有値問題式(
)を満足する
ようなものを直交する固有関数
と呼ぶ。結果論的には上の解法はいわゆるFourier級数
を用いた解法とみなせるが,
天下り的にFourier sine級数になるのではなく,
元の境界値問題に対応する固有値問題式(![]() ) (
) (![]() )から
自動的にsine関数で展開することが決定されているところに
留意して欲しい。対象や境界条件が異なれば当然,
この展開すべき固有関数も異なってくる。
ところで木琴ってどうなっているんだろう。
)から
自動的にsine関数で展開することが決定されているところに
留意して欲しい。対象や境界条件が異なれば当然,
この展開すべき固有関数も異なってくる。
ところで木琴ってどうなっているんだろう。