最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
初等梁理論ではせん断変形が生じないと仮定し,曲げには主に直応力で
抵抗するというモデル化を行うことによって,工学的な範囲内で精度
の良い直応力を比較的容易に算出できるようになった。
その影響線を用いて最大曲げモーメントを算定し,
発生する直応力で断面を設計すれば,曲げに抵抗する安全な梁の設計ができる。
しかし,断面にはせん断力![]() という抵抗力が生じていることから,
梁の内部にせん断応力も発生していることは明らかである。
例えばプレートガーダのウェブ板やウェブ・フランジの接合等の
安全性の確認には,せん断応力分布も求めておく必要がある。
という抵抗力が生じていることから,
梁の内部にせん断応力も発生していることは明らかである。
例えばプレートガーダのウェブ板やウェブ・フランジの接合等の
安全性の確認には,せん断応力分布も求めておく必要がある。
ではどうしたらいいだろう。一番確実なのは,梁理論を諦めて連続体として 曲げ部材の挙動を解くことだろう。しかし接合部の溶接だけを設計するために そのような計算をすることはあまり現実的ではない。 幸い我々が求めた梁理論による曲げ理論の直応力の精度はかなりいいことが わかっている。 それならば,その値は信じることにして,それに対するせん断応力を 求めることはできないだろうか。 我々が拠りどころにしているのは力のつり合いだ。 それなら,この直応力につり合うようなせん断応力を求めるというのは どうだろう。 それは多分,工学的に許容できる 第1次近似としての精度を持つせん断応力になる可能性がある。 そこで章-3の連続体の力学に戻り,梁理論で求められた 直応力につり合うようなせん断応力を求めてみよう。
図-4.65に示したように梁の内部の微分体積要素を
取り出すと,直応力![]() とつり合いの上で関連するせん断
応力は
とつり合いの上で関連するせん断
応力は![]() ,
, ![]() の二つである。
ただ
の二つである。
ただ![]() -
-![]() 面内での梁の曲げ問題で生じる
せん断力
面内での梁の曲げ問題で生じる
せん断力![]() は
は![]() 方向の力であり,それに対応するのは
図に太い矢印で示した
方向の力であり,それに対応するのは
図に太い矢印で示した![]() の方である。
またI形断面のプレートガーダ等を思い浮かべると,
そのウェブ部は
の方である。
またI形断面のプレートガーダ等を思い浮かべると,
そのウェブ部は![]() 方向の肉厚が非常に薄いため,
方向の肉厚が非常に薄いため,![]() の
大きさが
の
大きさが![]() の大きさより有意になるとは考え難い。
したがって,梁理論で次に重要な応力成分は
の大きさより有意になるとは考え難い。
したがって,梁理論で次に重要な応力成分は![]() の
方だと考え,初めのうちは
の
方だと考え,初めのうちは![]() を無視する。
を無視する。
![]() -
-![]() 面内の曲げ問題であることを考えると
面内の曲げ問題であることを考えると![]() 方向(肉厚
方向(肉厚![]() の方向)の
応力の分布を厳密に取り扱う必要が無いため,次の図-4.66に
示したように
の方向)の
応力の分布を厳密に取り扱う必要が無いため,次の図-4.66に
示したように
![]() の微分要素で
局所的なつり合いを考えても構わないだろう。
そういった意味で近似的なせん断応力を
扱っていることから,
の微分要素で
局所的なつり合いを考えても構わないだろう。
そういった意味で近似的なせん断応力を
扱っていることから,![]() の代わりに
の代わりに![]() という記号を用いる。
図の
という記号を用いる。
図の![]() 方向の力のつり合いは
方向の力のつり合いは
となる。ここに![]() は
は![]() 方向の単位体積当たりの
分布外力で,
方向の単位体積当たりの
分布外力で,![]() はその
はその![]() 方向の平均である。
図心を通るように
方向の平均である。
図心を通るように![]() 軸を配置させたときの梁理論の範囲内での
直応力は式(4.14b)で算定されているから,
これを上式に代入して左辺第2, 3項を右辺に移すと
軸を配置させたときの梁理論の範囲内での
直応力は式(4.14b)で算定されているから,
これを上式に代入して左辺第2, 3項を右辺に移すと
とも表現できる。これに梁理論での
つり合い式(4.18) (4.20)を代入して整理すると
となる。右辺の最後の項は体積力の![]() 方向平均と全断面平均との
差であり,第1次近似としては無視していい。
方向平均と全断面平均との
差であり,第1次近似としては無視していい。
上式(![]() )を,断面の上面
)を,断面の上面![]() から
から![]() 方向の任意の場所まで積分すると
方向の任意の場所まで積分すると
という関係を得る。![]() は
は![]() に関する積分のための補助変数である。
すなわち
に関する積分のための補助変数である。
すなわち![]() でのせん断応力がわかれば,梁理論で求められる
せん断力と断面形状のみによって断面内のせん断応力を計算できることになる。
通常,梁の上面には直接外力が作用することが無いと
考えていい4.11ため,
梁の上面はせん断応力に関しては自由表面である。
したがって上式(4.78)の左辺第2項は零と
なり,最終的に断面内のせん断応力分布は
でのせん断応力がわかれば,梁理論で求められる
せん断力と断面形状のみによって断面内のせん断応力を計算できることになる。
通常,梁の上面には直接外力が作用することが無いと
考えていい4.11ため,
梁の上面はせん断応力に関しては自由表面である。
したがって上式(4.78)の左辺第2項は零と
なり,最終的に断面内のせん断応力分布は
となる。ここに
で定義された関数は断面1次関数
と呼ばれる。この積分を断面の下端(![]() )まで
実行すると,
)まで
実行すると,
![]() であることに気が付けば
であることに気が付けば
となる。つまり,全断面積分したものが断面1次モーメントに
一致することが,その名前の由来である。
ここでは![]() 軸が図心を通るようにしているため,
せん断応力が断面下端
軸が図心を通るようにしているため,
せん断応力が断面下端![]() の自由表面でも零になることを確認できた。
の自由表面でも零になることを確認できた。
では図-4.67の左側に示した矩形断面の場合を
例にとり,せん断応力の分布を求めてみよう。
断面1次関数は
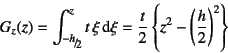
となり,
![]() であるから
であるから
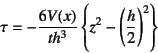
を得る。これは図-4.68に示したように断面
中央![]() で最大になるような
放物線分布であり,章-3の平面問題における
最後の例題での応力分布式(3.131b)と同じ形になっている。
この最大値は上式より
で最大になるような
放物線分布であり,章-3の平面問題における
最後の例題での応力分布式(3.131b)と同じ形になっている。
この最大値は上式より![]() で求められ
で求められ
となる。最後の式の![]() はせん断力を断面積
はせん断力を断面積![]() で
単純に除した平均せん断応力である。
念のために放物線分布の平均を算定してみると
で
単純に除した平均せん断応力である。
念のために放物線分布の平均を算定してみると
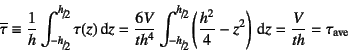
になっている。
求められたせん断応力分布を直応力と一緒に
図示したのが図-4.68である。
軸力が作用せず純粋に曲げのみが発生している場合には,
この図のように![]() 方向の直応力が図心で零になる三角形分布をし,
それにつり合うように求めた第1次近似としての
せん断応力分布は
方向の直応力が図心で零になる三角形分布をし,
それにつり合うように求めた第1次近似としての
せん断応力分布は![]() 軸上で最大値をとるような放物線分布をする。
なお
軸上で最大値をとるような放物線分布をする。
なお![]() 方向の直応力については,少なくとも構造力学としての
梁理論の範囲内での第1次近似は零と考えていいだろう。
方向の直応力については,少なくとも構造力学としての
梁理論の範囲内での第1次近似は零と考えていいだろう。
せん断応力は断面の上下面の自由表面では零になって
いるから,図-4.68に
示したように上下面では軸方向の直応力が最大あるいは
最小の主応力に一致し,主方向は![]() ,
, ![]() 方向になる。
これに対し
方向になる。
これに対し![]() 軸上では二つの直応力が零になり,
せん断応力の方は最大値をとる。したがってこの位置では
式(3.29) (3.30)を
用いると,主応力が
軸上では二つの直応力が零になり,
せん断応力の方は最大値をとる。したがってこの位置では
式(3.29) (3.30)を
用いると,主応力が
![]() ,
,
![]() となり,
主方向は
となり,
主方向は![]() 軸から
軸から![]() 度の方向になる。
例えばコンクリート材料のように引張りに非常に弱い材料で
梁ができている場合,梁の下面では
度の方向になる。
例えばコンクリート材料のように引張りに非常に弱い材料で
梁ができている場合,梁の下面では![]() 方向に最大の引張り主応力が
発生するため,もしひび割れ
が入るとしたら
方向に最大の引張り主応力が
発生するため,もしひび割れ
が入るとしたら![]() の負の方向に進展することが
予想される。一方断面の中央部ではその主引張り方向が
の負の方向に進展することが
予想される。一方断面の中央部ではその主引張り方向が![]() 軸
に対して45度傾いているため,梁の下面で発生したひび割れは
上方に進展するに従って曲がっていき,
図心位置では
軸
に対して45度傾いているため,梁の下面で発生したひび割れは
上方に進展するに従って曲がっていき,
図心位置では![]() 軸に45度傾いた方向に進展することも予想され,
確かに実験でも観察される。
軸に45度傾いた方向に進展することも予想され,
確かに実験でも観察される。
演習問題4-10の24番の
上フランジの厚さに相当する寸法![]() は,特に鋼構造の場合には非常に
小さくなっているのが普通である。
そういった部材を総じて薄肉断面部材
と呼んでいる。例えばI形断面の場合のせん断応力分布を
式(4.79)で計算したものを図-4.69に示した。
ウェブの部分では図に示したような値で分布するが,
せん断応力
は,特に鋼構造の場合には非常に
小さくなっているのが普通である。
そういった部材を総じて薄肉断面部材
と呼んでいる。例えばI形断面の場合のせん断応力分布を
式(4.79)で計算したものを図-4.69に示した。
ウェブの部分では図に示したような値で分布するが,
せん断応力![]() を
を![]() 方向に一様と仮定して定式化したことからも
当然なように,フランジとの接合部で不連続が
生じ,フランジ部分のせん断応力は比較的小さくなる。
しかも,ウェブと直接は接合されていない上フランジ
の
方向に一様と仮定して定式化したことからも
当然なように,フランジとの接合部で不連続が
生じ,フランジ部分のせん断応力は比較的小さくなる。
しかも,ウェブと直接は接合されていない上フランジ
の
![]() の突出部分は実はフランジ下面もせん断応力に
ついては
自由表面であることから,この図の細い線で描いたフランジ部分の
せん断応力分布が正しくないことは明らかである。
試しにウェブのせん断応力をウェブ部分だけで積分してみると,
フランジの部分が含まれていないのに
の突出部分は実はフランジ下面もせん断応力に
ついては
自由表面であることから,この図の細い線で描いたフランジ部分の
せん断応力分布が正しくないことは明らかである。
試しにウェブのせん断応力をウェブ部分だけで積分してみると,
フランジの部分が含まれていないのに
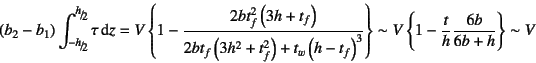
となる。ただし,上式と図中では
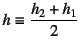 ,
,
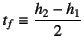 ,
,
![]() ,
,
![]() とした。
また最後から二番目の式ではウェブとフランジの肉厚を
どちらも
とした。
また最後から二番目の式ではウェブとフランジの肉厚を
どちらも![]() とした上で,
とした上で,![]() に比べて肉厚が非常に薄いとして
近似してある。
に比べて肉厚が非常に薄いとして
近似してある。
すなわち,薄肉のI形断面梁では
せん断力のほとんどすべてをウェブが受け持っている。
もちろん最大応力は長方形断面の場合と同様
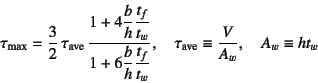
となるが, よく用いられている断面寸法の範囲では図-4.70に示したように 最大応力は平均応力の120%程度未満と考えられるため, 設計では平均せん断応力が用いられることが多い。したがって, フランジのせん断応力は零と考えてよく,フランジは直応力による抵抗を 主に受け持っているとみなしてもいい。 ただ鋼構造の場合,ウェブとフランジの接合部では薄板同士を溶接 してあることから,溶接ののど厚 を設計する場合等には,接合部のせん断応力も工学的な 範囲で精度良く求められていなければならない。
では,フランジ部分には全くせん断応力が発生してはいないのだろうか。
その答えは否である。前節でのせん断応力の誘導の一番
最初で![]() を
を![]() に比べて
比較的小さいものとして無視していたが,
フランジでは必ずしもそうではない。つまり,
フランジの
に比べて
比較的小さいものとして無視していたが,
フランジでは必ずしもそうではない。つまり,
フランジの![]() 方向の断面寸法(板厚)は
方向の断面寸法(板厚)は![]() 方向の
断面寸法(突出幅)よりも非常に小さいため,せん断応力の分布状況も
この寸法比率に近い大きさになっており,ウェブとは
逆に
方向の
断面寸法(突出幅)よりも非常に小さいため,せん断応力の分布状況も
この寸法比率に近い大きさになっており,ウェブとは
逆に![]() の方が
の方が![]() より有意になってくる。
もちろん
より有意になってくる。
もちろん![]() -
-![]() 面内で曲げを受ける梁理論の範囲内では,
面内で曲げを受ける梁理論の範囲内では,![]() 方向の
せん断力という断面の抵抗力を期待していないし,考える必要も無いため,
この
方向の
せん断力という断面の抵抗力を期待していないし,考える必要も無いため,
この![]() の断面内平均は零になることが容易に
予想できる。
の断面内平均は零になることが容易に
予想できる。![]() そのものも求める必要は無いかもしれないが,
その大きさと分布をここでは調べておきたい。
そのものも求める必要は無いかもしれないが,
その大きさと分布をここでは調べておきたい。
そこで少し一般化してフランジでもウェブでも通用し,
さらにI形断面以外の断面でも考え易い
ように,図-4.71のように薄板に沿った
断面内座標として![]() 軸を考え,この
軸を考え,この![]() -
-![]() 面内での
力のつり合いから梁理論で求められた直応力
面内での
力のつり合いから梁理論で求められた直応力![]() に
つり合うようなせん断応力
に
つり合うようなせん断応力![]() を求めておこう。
もちろん前出のI形断面のフランジやウェブの場合には,
この
を求めておこう。
もちろん前出のI形断面のフランジやウェブの場合には,
この![]() 軸はそれぞれで
軸はそれぞれで![]() 軸あるいは
軸あるいは![]() 軸に
平行になる。また図にも示したように,肉厚方向の分布を
無視して平均的な応力のみを考えるために,せん断応力を
ここでも
軸に
平行になる。また図にも示したように,肉厚方向の分布を
無視して平均的な応力のみを考えるために,せん断応力を
ここでも![]() と表記する。体積力は式(4.78)の
誘導でも無視できたので,最初から考えないで,
前節と同様に
と表記する。体積力は式(4.78)の
誘導でも無視できたので,最初から考えないで,
前節と同様に![]() 方向の力のつり合いをとると
方向の力のつり合いをとると
であるから,![]() について積分することにより最終的にせん断応力が
について積分することにより最終的にせん断応力が
となる。ここに![]() は
は![]() 軸に沿って積分するときの起点の座標値であり
軸に沿って積分するときの起点の座標値であり
は![]() の関数としての断面1次関数である。また
の関数としての断面1次関数である。また![]() は
は![]() に
関する積分の補助変数であり,
に
関する積分の補助変数であり,![]() も
も![]() の関数として取り扱うように
パラメトリック表示してある。
形式的には式(4.79)と同じである。
の関数として取り扱うように
パラメトリック表示してある。
形式的には式(4.79)と同じである。
より一般的な薄肉断面の場合,特に閉断面の
場合については別途参考書を参照して欲しい。
ここではI形断面のような薄板の集合として作られた開断面のみを
対象とする。
その場合,図-4.72に示したように
ウェブとフランジの板同士の接合点が存在する。
上フランジではそれぞれの突出端がせん断応力に関しては
自由表面なので,そこから![]() ,
, ![]() 軸を定義して
それぞれの分布を算定すればいい。
これに対しウェブとの接合点では,
応力の連続性から
軸を定義して
それぞれの分布を算定すればいい。
これに対しウェブとの接合点では,
応力の連続性から![]() 方向への積分の起点での
条件を求めなければならない。
そこで同図の右図のように接合点近傍の微分要素を取り出して,
この要素の
方向への積分の起点での
条件を求めなければならない。
そこで同図の右図のように接合点近傍の微分要素を取り出して,
この要素の![]() 方向の力のつり合いをとると
方向の力のつり合いをとると
が成立しなければならない。ここに![]() はそれぞれの区間の
肉厚である。第1項の直応力の部分は第2項に比べると高次項なの
で無視すると,結局接合点では
はそれぞれの区間の
肉厚である。第1項の直応力の部分は第2項に比べると高次項なの
で無視すると,結局接合点では
と定義しておくと,上の連続条件は
とも表現できる。すなわち,式(4.83)で定義した せん断流が,このT字形の断面をあたかも水路のように考えたときの, その分岐点での水の流れの連続性と同じになっている。
図-4.69にあるような
薄肉の2軸対称I形断面を例にして,せん断応力の
分布を求めてみよう。![]() の座標を図-4.73に
明示した。
の座標を図-4.73に
明示した。![]() の始点は自由表面に
当たるので
の始点は自由表面に
当たるので
![]() となり
となり
であるから
となる。![]() も同様で,
も同様で,
![]() であることに注意すれば
であることに注意すれば
を得る。次に![]() についても
についても
![]() であることに
注意すれば,上の誘導とほとんど同じ計算をすればよく
であることに
注意すれば,上の誘導とほとんど同じ計算をすればよく
となる。同様に![]() についても
についても
を得る。
![]() ,
, ![]() と
と![]() の接点では式(4.84)で
示した連続条件が成立しなければならないから,
上で得た結果を代入すると
の接点では式(4.84)で
示した連続条件が成立しなければならないから,
上で得た結果を代入すると
となる。これで![]() 方向への始点でのせん断流の値が求められた。
よって
方向への始点でのせん断流の値が求められた。
よって
と表現でき,
![]() だから
だから
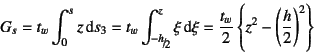
が断面1次関数になる。したがって,ウェブ内のせん断応力分布は
になる。分布を図示したのが図-4.73の右側の図である。
まずウェブのせん断応力分布を見てみよう。
ウェブ上下端のせん断応力値とウェブ中央でのせん断応力の最大値とは
それぞれ
になっている。前者は図-4.69に
示したせん断応力の値と一致している。
後者の最大値は図-4.69で示した
ものの![]() を
を![]() で置き換えたものになるが,
で置き換えたものになるが,![]() で
あることから,薄肉断面である限りこの2者の差は非常に小さく
両者は一致していると考えていい。
つまりウェブだけに着目すれば,フランジの肉厚が薄い限り
前節のせん断応力の算定で十分であることも明らかになった。
試しに
で
あることから,薄肉断面である限りこの2者の差は非常に小さく
両者は一致していると考えていい。
つまりウェブだけに着目すれば,フランジの肉厚が薄い限り
前節のせん断応力の算定で十分であることも明らかになった。
試しに![]() をウェブ断面内で積分すると,
この場合には正確に
をウェブ断面内で積分すると,
この場合には正確に![]() に一致する。
に一致する。
次に,
ここで新たに導出されたフランジにおける有意な
せん断応力成分![]() は,図-4.73に
示したように分布していることになる。
この分布は断面内ですべて総和をとると零になるように,
お互いのフランジ突出部分同士で打ち消しあっている。
したがって,断面力としての
は,図-4.73に
示したように分布していることになる。
この分布は断面内ですべて総和をとると零になるように,
お互いのフランジ突出部分同士で打ち消しあっている。
したがって,断面力としての![]() 方向成分が存在しないこととも
整合している。
この
方向成分が存在しないこととも
整合している。
この
![]() がウェブとフランジの接合点に生じている。
したがってここの溶接ののど厚等を設計する場合には,
この値を用いればいいことになる。
実は第1著者は,何故こんなところに断面2次モーメントがつくのかわからなかった。
がウェブとフランジの接合点に生じている。
したがってここの溶接ののど厚等を設計する場合には,
この値を用いればいいことになる。
実は第1著者は,何故こんなところに断面2次モーメントがつくのかわからなかった。
もう一つの代表例の溝形断面の場合は,図-4.74のようにI形断面と
同じように計算をすると,
次の演習問題4-11に示した通りになる。
この場合は分岐点が無いので計算は楽だ。
このせん断応力分布が作る![]() 方向の合応力が零になり,
方向の合応力が零になり,![]() 方向の
合応力が
方向の
合応力が![]() になることも容易に確かめることができる。
さてそれでは,原点O回りのモーメントを算定してみよう。
これも容易に積分でき,結果は
になることも容易に確かめることができる。
さてそれでは,原点O回りのモーメントを算定してみよう。
これも容易に積分でき,結果は
となってしまう。すなわち![]() -
-![]() 面内で曲げを受ける梁の挙動を
問題の対象にしているにもかかわらず,この棒は
原点回りに(図心回りであっても零にならない)ねじり抵抗
モーメントを発生させている。逆に考えると,図心あるいは原点を
作用線が通るようなせん断力を与えて曲げのみを与えた場合であっても,
棒はねじれてしまう。2軸対称ではない断面は神秘的だ。
面内で曲げを受ける梁の挙動を
問題の対象にしているにもかかわらず,この棒は
原点回りに(図心回りであっても零にならない)ねじり抵抗
モーメントを発生させている。逆に考えると,図心あるいは原点を
作用線が通るようなせん断力を与えて曲げのみを与えた場合であっても,
棒はねじれてしまう。2軸対称ではない断面は神秘的だ。
このように2軸対称ではない断面を持つ棒に
曲げを加えた場合には,一般に棒はねじれる。
では,ねじれないように棒を曲げるにはどうしたらいいか。
それは式(![]() )の
ねじりモーメントが零になるようにせん断力が発生(作用)すれば
いい。この場合は図-4.74の左図に示した点Sに
せん断力が作用するようにすれば,ねじれることがなくなる。
この点Sをせん断中心
と呼び,溝形断面の場合には
)の
ねじりモーメントが零になるようにせん断力が発生(作用)すれば
いい。この場合は図-4.74の左図に示した点Sに
せん断力が作用するようにすれば,ねじれることがなくなる。
この点Sをせん断中心
と呼び,溝形断面の場合には
の位置になる。より一般的なせん断中心の定義については 別途参考文献あるいは章-7を参照のこと。 対傾構のような2次部材には形鋼を用いることがあるが, 溝形鋼や山形鋼は突出辺が 片方だけなのでI形断面やH形鋼より接合が楽になる利点がある。 しかし,立体骨組としてそれを解析するときには,上述のように 多少面倒なことがありそうなので注意が必要だ。
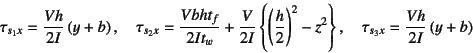
となることを示せ。
ここまでに説明した
初等梁理論の枠内ではせん断変形を無視し,
せん断力は
![]() のように
軸線方向への一様ではない曲げモーメントに対する反力的な
存在だったが,
高次理論としてせん断変形を許す理論もある。
代表的かつ有名なのはTimoshenko梁理論
と呼ばれているもので,断面に一様なせん断変形が
生じると仮定する理論である。図-4.75に簡単な概念を
示したが,変形した梁の軸線と断面の法線ベクトル
のように
軸線方向への一様ではない曲げモーメントに対する反力的な
存在だったが,
高次理論としてせん断変形を許す理論もある。
代表的かつ有名なのはTimoshenko梁理論
と呼ばれているもので,断面に一様なせん断変形が
生じると仮定する理論である。図-4.75に簡単な概念を
示したが,変形した梁の軸線と断面の法線ベクトル![]() とが
一致せず,断面に一様なせん断変形
とが
一致せず,断面に一様なせん断変形![]() が発生し得る
モデルである。
これ自体は前節で求められた放物線分布を示すせん断応力とは
整合せず,また上下縁でせん断応力が零にならないことも
力学的にはおかしく,無理な近似ではあるものの,
こうすることによってせん断力をせん断応力で定義できる
理論4.12になる。
が発生し得る
モデルである。
これ自体は前節で求められた放物線分布を示すせん断応力とは
整合せず,また上下縁でせん断応力が零にならないことも
力学的にはおかしく,無理な近似ではあるものの,
こうすることによってせん断力をせん断応力で定義できる
理論4.12になる。
ひずみ場の仮定で式(4.1) (4.2)と異なるのは
せん断ひずみ成分![]() であり,したがって応力成分もせん断応力
成分が存在する。つまり
であり,したがって応力成分もせん断応力
成分が存在する。つまり
と仮定する。対応する変位場も式(4.3)に代って
となる。これから軸方向のひずみ成分は
のように第3項にせん断変形の影響が加わる。さらに,
曲げモーメントと変位の関係式(4.13b)は
で置き換わる。またせん断力はもはや曲げモーメントの
反力的な断面力ではなく,上のせん断応力の断面内の合応力として
で定義できる。この![]() は単純な計算からは
は単純な計算からは![]() で
なければならないが,実際には図-4.68のように断面内で
非一様に分布するはずのせん断変形を,図-4.75の
ような断面内一定のせん断変形
で
なければならないが,実際には図-4.68のように断面内で
非一様に分布するはずのせん断変形を,図-4.75の
ような断面内一定のせん断変形![]() で胡麻化してしまったため,
それを補正するために別途導入された係数である。値そのものは
断面形状とPoisson比
で胡麻化してしまったため,
それを補正するために別途導入された係数である。値そのものは
断面形状とPoisson比![]() に依存する定数[16]で,例えば
に依存する定数[16]で,例えば
といった値を持つ。
ただし,節-4.6.1で求めた,
せん断応力の最大値と平均値の関係を表す係数(矩形の場合の![]() )とは
全く関係ないことには注意する。
)とは
全く関係ないことには注意する。
以上のような誘導から得た主な支配方程式を
文献[126]を真似て無次元化して表示すると
となる。ここに
と定義し直した。上式の下線部が初等梁理論の範囲であり,それ以外が
せん断変形の影響を代表している項である。式中の
![]() は
は
(4.85)
で定義した。
![]() はTimoshenko梁の細長さの特性を表す一種の細長比
である。多くの構造力学公式集等では
はTimoshenko梁の細長さの特性を表す一種の細長比
である。多くの構造力学公式集等では![]() 中のPoisson比を
無視したものが記載されていることが多いため,
ここでも幾何量である細長比
中のPoisson比を
無視したものが記載されていることが多いため,
ここでも幾何量である細長比
![]() の方に組み込んである。
これだけでは,分布外力
の方に組み込んである。
これだけでは,分布外力![]() が存在しなければ初等梁理論の
支配方程式と一致しそうに見えるが,付録-Dの
式(D.3)にあるように,断面の回転とたわみの関係に
せん断変形が含まれているため,分布外力が無くても境界条件に違いが
現れ,それを通して解は初等梁理論のものとは異なる。
が存在しなければ初等梁理論の
支配方程式と一致しそうに見えるが,付録-Dの
式(D.3)にあるように,断面の回転とたわみの関係に
せん断変形が含まれているため,分布外力が無くても境界条件に違いが
現れ,それを通して解は初等梁理論のものとは異なる。
等方弾性体の関係
![]() を用いるなら,
例えば矩形断面の場合には
を用いるなら,
例えば矩形断面の場合には
という関係になる。![]() は一般に細長比と
呼ばれているものであり,純粋に断面の代表寸法と梁の長さの比である。
上の支配方程式からも明らかなように,せん断変形の影響は
は一般に細長比と
呼ばれているものであり,純粋に断面の代表寸法と梁の長さの比である。
上の支配方程式からも明らかなように,せん断変形の影響は
![]() が
相対的に大きい場合に顕著になることがわかる。
逆に言うと
が
相対的に大きい場合に顕著になることがわかる。
逆に言うと
![]() が小さい限り,つまり
が小さい限り,つまり
である限り,初等梁理論で十分な精度の解を得ることができることがわかる。 この二つ目の条件は,幾何学的条件によって力学挙動が 一見変わって見えるという面白い結果であるが, 梁に対して用いた基本的な仮定のうちの一つのBernoulli-Eulerの 仮定を裏付けるものである。
例えば単純支持梁中央に荷重![]() を載せた3点曲げの問題は,
半分の長さの片持ち梁の先端に
を載せた3点曲げの問題は,
半分の長さの片持ち梁の先端に![]() を載せた問題と同じになるので,
それを解くと,3点曲げの中央のたわみは
を載せた問題と同じになるので,
それを解くと,3点曲げの中央のたわみは
となる。第1項はBernoulli-Euler梁の解であり,第2項がせん断変形の
影響である。半スパンはせん断力![]() 一様な場なので,
一様なせん断変形
一様な場なので,
一様なせん断変形
![]() が生じ,
これによる中央のたわみがその
が生じ,
これによる中央のたわみがその
![]() 倍になっているというのが,
この第2項である。
ただし不静定梁のような一般的な場合のたわみは,
曲げ変形によるたわみとせん断変形によるたわみの和にはならないことには
注意すること。
倍になっているというのが,
この第2項である。
ただし不静定梁のような一般的な場合のたわみは,
曲げ変形によるたわみとせん断変形によるたわみの和にはならないことには
注意すること。
実用的には,このようにしてせん断変形の影響を入れた解とそうでない
初等梁理論の解との差は
![]() 程度,すなわち
細長比の2乗に逆比例した程度で
ある。1例として図-4.76に簡単な問題の結果を
示しておいたが,この程度の影響に過ぎない。
したがって,極端に短い梁の挙動を調べたり
梁の衝撃外力に対する応答あるいは高周波振動等を対象とする
場合を除き,Timoshenko梁理論を用いる必要は無い。
詳細については参考文献[126]等を参照のこと。
程度,すなわち
細長比の2乗に逆比例した程度で
ある。1例として図-4.76に簡単な問題の結果を
示しておいたが,この程度の影響に過ぎない。
したがって,極端に短い梁の挙動を調べたり
梁の衝撃外力に対する応答あるいは高周波振動等を対象とする
場合を除き,Timoshenko梁理論を用いる必要は無い。
詳細については参考文献[126]等を参照のこと。
結局,初等梁理論は
という理論であった。
しかし模式図-4.77のような,比較的
幅の広い断面の梁4.13を対象とする場合には,この幅の広いフランジ部分に
発生するせん断応力![]() による(床版が平板として挙動する)影響が
無視できない場合がある。
つまり,全部の断面が初等梁理論の範囲内で抵抗すると仮定して
求められる直応力分布(図中の一点鎖線)
による(床版が平板として挙動する)影響が
無視できない場合がある。
つまり,全部の断面が初等梁理論の範囲内で抵抗すると仮定して
求められる直応力分布(図中の一点鎖線)
![]() よりも
大きな直応力(図の縦軸は圧縮を正にした値である)が主桁部に生じ,
図の曲線のように,
その直応力分布は幅方向に一様ではなくなることがわかっている。
よりも
大きな直応力(図の縦軸は圧縮を正にした値である)が主桁部に生じ,
図の曲線のように,
その直応力分布は幅方向に一様ではなくなることがわかっている。
このような現象をせん断遅れ
と呼んでいるが,正確に応力分布を求める方法等については
参考文献[141]等を参照して欲しい。
実際の設計においては,上フランジの一部を無視し,
各T形部分を中心にしてある適当な幅![]() の上フランジを持つT形梁に置き換え,
それに初等梁理論を適用して直応力分布の最大値を簡便に計算する手法が
よく用いられている。
図の上方の水平な実線がその値である。この
の上フランジを持つT形梁に置き換え,
それに初等梁理論を適用して直応力分布の最大値を簡便に計算する手法が
よく用いられている。
図の上方の水平な実線がその値である。この![]() を有効幅
と呼んでいる。これも詳細については参考文献等を参照のこと。
を有効幅
と呼んでいる。これも詳細については参考文献等を参照のこと。