 |
最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
章-4では,梁の軸線と断面の直交性が 変形後も保持されるという, いわゆるBernoulli-Euler梁の定式化をした。 その仮定の範囲内で求められる直応力とつり合うせん断応力が 放物線分布することは,節-4.6.1で示した通りで, しかもそれは平面問題の解式(3.131b)とも整合していた。 より(連続体力学として)正確な梁理論を求めたければ, この放物線分布に対応するせん断変形を予め考慮して梁理論の定式化を し直せばいいが,ここではもっと簡便な古典的理論を誘導する。
その理論はTimoshenko梁理論と呼ばれ,Bernoulli-Eulerの仮定を
緩め,ある断面には一様なせん断変形が発生すると仮定する。
すなわち基本的な仮定のうちの式(4.2)の代わりに
を前提とする。
ただ,梁の上下面には直接外力が作用することは無いことから
せん断ひずみも零になり,
この断面内一様なせん断ひずみ分布は物理的には容認できない。
しかし,せん断変形は細長い梁にとっては二次的なものであり,
この程度の差異について別途調整(後述の![]() の導入)ができるなら,
これで簡便でかつ精度の良いモデルが構築できるとも考えられる。
の導入)ができるなら,
これで簡便でかつ精度の良いモデルが構築できるとも考えられる。
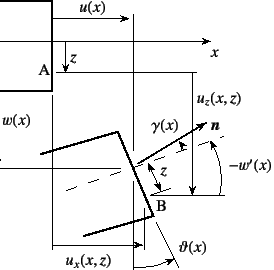
この仮定に従って梁の運動を記述したのが図-D.1である。
図から明らかなように,断面内任意点の![]() ,
, ![]() 方向変位成分は
微小変位の範囲内で,これも式(4.3)の代わりに
方向変位成分は
微小変位の範囲内で,これも式(4.3)の代わりに
となる。ここに![]() は,軸のたわみ角ではなく断面の
回転角を表している。式(D.1)左辺に
式(3.6)の定義を用いて式(D.2)を代入すると
は,軸のたわみ角ではなく断面の
回転角を表している。式(D.1)左辺に
式(3.6)の定義を用いて式(D.2)を代入すると
となる。ここにプライムは![]() に関する微分を表す。
つまり,式(4.4)の
に関する微分を表す。
つまり,式(4.4)の![]() に代る
に代る![]() は
たわみ角
は
たわみ角![]() には一致せず,せん断変形分
には一致せず,せん断変形分![]() だけずれる。
以上より,伸びひずみは
だけずれる。
以上より,伸びひずみは
となる。
直応力は1次元のHookeの法則式(3.116a)に,
せん断応力はHookeの法則式(3.42)に従うものとすれば,
以上のひずみ成分をそれに代入することによって
となる。ここに![]() と
と![]() はそれぞれYoung率とせん断弾性
係数である。
はそれぞれYoung率とせん断弾性
係数である。![]() 軸が図心を通るように選べば,
これを用いて断面に発生する合応力は
軸が図心を通るように選べば,
これを用いて断面に発生する合応力は
と定義され,変位と関係付けられる。
ただし簡単のために均質材料でできた等断面の梁とした。
また,式(D.6c)の![]() は定義通りなら1になるはずだが,
前述のように本来一様ではない断面内のせん断変形を
一様な場
は定義通りなら1になるはずだが,
前述のように本来一様ではない断面内のせん断変形を
一様な場![]() で近似したことを補正するために
導入された係数(節-4.6.2に例がある)で,
断面形状とPoisson比に依存する定数[16]である。
で近似したことを補正するために
導入された係数(節-4.6.2に例がある)で,
断面形状とPoisson比に依存する定数[16]である。
つり合い式と境界条件は,付録-Cと同様,3次元の
仮想仕事式に前節の変位場・ひずみ場と断面力の
定義とを代入すれば求めることができるが,ここではその詳細は省略し,
結果のみを列挙しておく。
断面力で表したつり合い式はBernoulli-Euler梁と同じ
式(4.17) (4.18) (4.20)で
表され
である。境界条件は,たわみ角の境界条件を除けば他は
式(4.23)と同じである。
ここではせん断変形を許しているので,梁の中間載荷点等では
軸線が滑らかでたわみ角が連続するとは限らないが,その代わりに
断面の回転角![]() は連続しなければ,連続体としての梁の
連続性は失われてしまう。したがって,たわみ角の代わりに
は連続しなければ,連続体としての梁の
連続性は失われてしまう。したがって,たわみ角の代わりに![]() を
与える条件で,モーメントの境界条件に対応する変位の境界条件は
与えられるはずである。つまり
を
与える条件で,モーメントの境界条件に対応する変位の境界条件は
与えられるはずである。つまり
となる。ここに![]() は式(4.24)で
定義した記号であり,
は式(4.24)で
定義した記号であり,![]() 等は端部で与える変位量である。
回転角についての境界条件については,
等は端部で与える変位量である。
回転角についての境界条件については,![]() そのものや
そのものや![]() を
与えるようなことはできないし,
この2者が中間載荷点や中間支点で連続になる必要も無いことには
十分注意する。
を
与えるようなことはできないし,
この2者が中間載荷点や中間支点で連続になる必要も無いことには
十分注意する。
前節で示したように,軸圧縮の問題は曲げの問題と連成しないばかりか
初等梁理論のそれと一致しているので,ここからは曲げ問題のみに
焦点を絞ることにする。不静定構造を解くことを念頭に置いて,
曲げ問題の支配方程式をたわみ![]() で表しておく。
式(D.6)を式(D.7) (D.8)に
代入し,式(D.3)を考慮して
で表しておく。
式(D.6)を式(D.7) (D.8)に
代入し,式(D.3)を考慮して![]() と
と![]() を
消去すると,つり合い式は
を
消去すると,つり合い式は
となり,境界条件
式(D.8)は
と表わされる。ここに
と定義したが,
![]() は式(4.85a)で
定義したパラメータである。
は式(4.85a)で
定義したパラメータである。![]() の
極限で
の
極限で
![]() になり,上式は
すべて初等梁理論の支配方程式に一致する。
になり,上式は
すべて初等梁理論の支配方程式に一致する。