�ŐV�ł𐳊m�ɓǂޏꍇ�ɂ� pdf �t�@�C�� ���ǂ����B����� web �����̂��߂̊ȈՋ��łł��B
�ÓI�Ȗ��͂��Ƃł�邱�Ƃɂ��āC
��(3.22)�̉��͂̂荇�����I�Ȗ��ɑ���
�g�����悤�B���̂��߂ɂ�Newton�̖@���ɏ]���ĉE�ӂɊ����͍�������������B
�܂�C���x��![]() �Ƃ����
�Ƃ����
�ƂȂ�B��ɕt�����h�b�g�͎��Ԕ����ł���B
����Ɏ�(3.42)��Hooke�̖@���������C
��(3.6)�̂Ђ��݂̒�`���������
![\begin{displaymath}
\mu\sum_j\left( \D[2][1][x_i]{u_j}{x_j}+\D[2]{u_i}{x_j}\right)
+\lambda\sum_j\D[2][1][x_i]{u_j}{x_j}+X_i=\rho \ddot{u}_i
\end{displaymath}](s1img927.gif)
�ƂȂ�B�����ŁC�ψʏꂪHelmholtz����藝
��p����2��ނ̃|�e���V�����ŗ^������Ƃ����
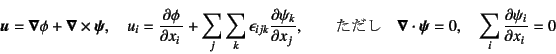 |
(3.97) |
�ƒu�����Ƃ��ł���B���l�ɕ��z�O�͂������ł���Ƃ���
| (3.98) |
�ƒu�����Ƃ��ł�����̂Ƃ���B
����2������̉^���������ɑ�����Ď�̉��Z������ƁC
�ŏI�I�Ɏ��̂悤�ɂȂ�B
![\begin{displaymath}
\D{}{x_i} \left\{ (\lambda+2\mu) \sum_j \D[2]{\phi}{x_j}
+...
...sum_j \D[2]{\psi_l}{x_j} + G_l
- \rho \ddot\psi_l \right\}=0
\end{displaymath}](s1img930.gif)
������C���z�O�͂������ꍇ��2��ނ̃|�e���V�������������ׂ�����
�ƂȂ�C2��ނ��g�������� �̊�{�I�Ȍ`���邱�Ƃ��ł���B������
(3.100)
���ʑ����x
�i�g�̓`��鑬�x�j�ŁC![]() �͏c�g
���邢�͑̐ϔg�iPressure�g�G�n�k�g�Ȃ�Primary�g�CP�g�j��
�ʑ����x�C
�͏c�g
���邢�͑̐ϔg�iPressure�g�G�n�k�g�Ȃ�Primary�g�CP�g�j��
�ʑ����x�C![]() �͉��g
���邢�͂���f�g�iShear�g�G�n�k�g�Ȃ�Secondary�g�CS�g�j�̈ʑ����x�ł���B
�͉��g
���邢�͂���f�g�iShear�g�G�n�k�g�Ȃ�Secondary�g�CS�g�j�̈ʑ����x�ł���B
�O�߂Ɠ����悤�ȍl�@�𗬑̂ɑ��Ď��݂悤�B��ʂɗ��̂͂ق�
�k�������ƃ��f���������̂ŁC��(3.14)��
�̐ςЂ��݂���ɗ�ł���B���̂̏ꍇ�͂Ђ��݂��̂��̂��Ђ���
���x�ɒ��ڂ���̂ŁC�ψʂł͂Ȃ����x���k��
���`��������
�ƂȂ�B������![]() �͑��x�x�N�g���ł���C
���̏��������C��ɗ��̉�������A���̎�
�ƌĂԂ��Ƃ�����B
�����Ȃ�Ǝ�(3.42)��Hooke�̖@���̉E�ӑ�2����
�Ӗ����������C�̐ς��ω����Ȃ��悤�ɗ��̂���R��
���Ă���C���ꂪ�ޗ��̒�R�����Ƃ͊W�̖���
�Ɨ��Ȋ��u�Ð���
�͑��x�x�N�g���ł���C
���̏��������C��ɗ��̉�������A���̎�
�ƌĂԂ��Ƃ�����B
�����Ȃ�Ǝ�(3.42)��Hooke�̖@���̉E�ӑ�2����
�Ӗ����������C�̐ς��ω����Ȃ��悤�ɗ��̂���R��
���Ă���C���ꂪ�ޗ��̒�R�����Ƃ͊W�̖���
�Ɨ��Ȋ��u�Ð���![]() �v�Ƃ��đ��݂��邱�ƂɂȂ�B
�܂莮(3.40)��
�v�Ƃ��đ��݂��邱�ƂɂȂ�B
�܂莮(3.40)��![]() �ł���
�Ȃ���
�ł���
�Ȃ���![]() ���L�E�ő��݂���ޗ����k���ޗ��ł���B
���Ȃ킿
���L�E�ő��݂���ޗ����k���ޗ��ł���B
���Ȃ킿![]() �C����Ɏ�(3.44d)���
�C����Ɏ�(3.44d)���
![]() �ł���
�悤�ȍޗ��ɑ�������B
���������āC���͂Ђ��݊W��(3.42)��
�ł���
�悤�ȍޗ��ɑ�������B
���������āC���͂Ђ��݊W��(3.42)��
�Ƃ��Ȃ���Ȃ�Ȃ��B������![]() �����k�𐳂ɂ����ʏ�̐Ð���
�ł���B
���̏ꍇ��
�����k�𐳂ɂ����ʏ�̐Ð���
�ł���B
���̏ꍇ��![]() �͂Ђ��ݑ��x�ɔ�Ⴕ����R���W���Ȃ̂�
�S���W���ł���BHooke�̖@������(3.102)��
�u����������ʼn^���������ɑ�����C���z�O�͂����̂�
���d�����Ȃ�
�͂Ђ��ݑ��x�ɔ�Ⴕ����R���W���Ȃ̂�
�S���W���ł���BHooke�̖@������(3.102)��
�u����������ʼn^���������ɑ�����C���z�O�͂����̂�
���d�����Ȃ�
![]() �ƒu����̂�
�ƒu����̂�
�ƂȂ�B�����Navier-Stokes�̎� �Ƃ��Ēm���Ă���B
�Ƃ���ŗ��̂̏ꍇ�C���x�͗��̒��̗��q�̑��x�Ƃ������C
�ώ@���Ă���_�́i�K���X�̐����̑��ʂɃ}�[�N���L���C������
���ۂ��ώ@�����j���x�ł���B�������C�������̑��x��
���Ԕ����͗��q�̉����x�łȂ���Ȃ炸�C���Ǐ㎮��
�h�b�g����������
�܂�
�Ƃ���K�v������B��(3.104)�̉E�ӑ�2�����ڗ���
�ƌĂ��B
�ʏ�C�ő̗͊w�������_�i![]() ���ő̒���
���q�ɕt�������O�ł���j��ǐՂ���Lagrange��@
���Ƃ�̂ɑ��C���̗͊w�ł͋�Ԉʒu�i
���ő̒���
���q�ɕt�������O�ł���j��ǐՂ���Lagrange��@
���Ƃ�̂ɑ��C���̗͊w�ł͋�Ԉʒu�i![]() �͗��̂Ƃ͊W����
��ԓ��̊ϑ��ʒu�ł���j�Ō��ۂ𑨂���Euler��@
��p����B
�͗��̂Ƃ͊W����
��ԓ��̊ϑ��ʒu�ł���j�Ō��ۂ𑨂���Euler��@
��p����B
����ɔS���������Ȃ�(![]() )���S����
�ɁC�X�J���[�|�e���V����
)���S����
�ɁC�X�J���[�|�e���V����![]() �݂̂�
�^������i���]��
�ɑΉ������j���z�O��
�݂̂�
�^������i���]��
�ɑΉ������j���z�O��
��������p���C
����ɒ���Ԃɂ���(
![]() )�ꍇ�ɂ́C
��(3.103)��Navier-Stokes�̎���
��(3.104)���l�����ĉ��Z�������ƁC���������
)�ꍇ�ɂ́C
��(3.103)��Navier-Stokes�̎���
��(3.104)���l�����ĉ��Z�������ƁC���������
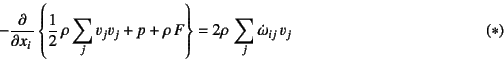
�ƂȂ�B������
![]() ���X�s��
�e���\���������`���I�ɕ\�������̂�
���X�s��
�e���\���������`���I�ɕ\�������̂�
�ł���B�㎮(![]() )�̊��ʓ���1���͑��x�x�N�g���̑傫����2��ɂȂ��Ă���
�̂ŒP��
)�̊��ʓ���1���͑��x�x�N�g���̑傫����2��ɂȂ��Ă���
�̂ŒP��![]() �ƋL�����Ƃɂ���B�������]�̉^���������Ă��Ȃ�
�ꍇ�ɂ͉E�ӂ�
�ƋL�����Ƃɂ���B�������]�̉^���������Ă��Ȃ�
�ꍇ�ɂ͉E�ӂ�
![]() �͗�ɂȂ�C���ǂ�����Ƃ����
�͗�ɂȂ�C���ǂ�����Ƃ����
�ł���B�������z�O�͂��d�͏�ł̎��d�݂̂ł���C�d��
�����x![]() ��p����
��p����![]() �ƒu���Ă悭�C�㎮��
�ƒu���Ă悭�C�㎮��
�ƂȂ�B�����Bernoulli�̎�
�ł���B���]���ł͂Ȃ��ꍇ�ɂ́C�㎮(![]() )�E�ӂ𐬕��Ƃ���
�x�N�g���Ƒ��x�x�N�g���̓��ς���ɂȂ邱�Ƃ���C����
�ɉ�����Bernoulli�̎����������邱�ƂɂȂ�B
���̗͊w�i�����w�j���ό`�ł��镨�̗̂͊w�ł��邱�Ƃ��킩��Ǝv���B
)�E�ӂ𐬕��Ƃ���
�x�N�g���Ƒ��x�x�N�g���̓��ς���ɂȂ邱�Ƃ���C����
�ɉ�����Bernoulli�̎����������邱�ƂɂȂ�B
���̗͊w�i�����w�j���ό`�ł��镨�̗̂͊w�ł��邱�Ƃ��킩��Ǝv���B
�����ł͌ő̖̂��Ɍ��肵�C������3�������ł���Ȃ���C��������� ���镽�ʏ�̖��Ƃ��đ����邱�Ƃ��ł���ꍇ��ΏۂƂ��C ���͊��ɂ���@��Ꭶ����B���ʖ��ł����Ă����̂�3�����I�� ��R���ĉ^������̂ŁC2�������ƌĂ�ł͂����Ȃ��B
�����C![]() �����ւ̕��̂̊g�������l�ł�����2�������
�ɒ[�ɑ傫�����̂̏ꍇ�C
�����ւ̕��̂̊g�������l�ł�����2�������
�ɒ[�ɑ傫�����̂̏ꍇ�C![]() �����̕ψʂ͖����ł���ق�
�������C�܂����͂�Ђ��݁E�ψʂ�
�����̕ψʂ͖����ł���ق�
�������C�܂����͂�Ђ��݁E�ψʂ�![]() �ɂ͈ˑ����Ȃ����i
�ɂ͈ˑ����Ȃ����i![]() �����ɂ�
���j�Ƃ��đ����邱�Ƃ��ł���B�܂�u�����Y���v
�̂���f�ʓ��ł̌��ۂ�Ώۂɂ���悤�Ȃ��̂ł���B
���̂悤�ȏꍇ�����ʂЂ���
��ԂƌĂԁB���Ȃ킿�C�ψʂɑ���
�����ɂ�
���j�Ƃ��đ����邱�Ƃ��ł���B�܂�u�����Y���v
�̂���f�ʓ��ł̌��ۂ�Ώۂɂ���悤�Ȃ��̂ł���B
���̂悤�ȏꍇ�����ʂЂ���
��ԂƌĂԁB���Ȃ킿�C�ψʂɑ���
| (3.106) |
�Ƃ���������ꍇ�ɑ�������B���������Ď�(3.42)�ɑ������
 |
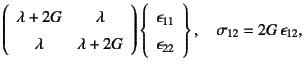 |
(3.107) | |
| (3.108) |
�Ƃ����W��B���ꂩ��C![]() -
-![]() ���ʓ��ł̋t�W
�́C��(3.44)�Œ�`����Poisson���p�����
���ʓ��ł̋t�W
�́C��(3.44)�Œ�`����Poisson���p�����
�ƂȂ�B���̊W���㎮��![]() �̉E�ӂɑ�����邱�Ƃɂ����
�̉E�ӂɑ�����邱�Ƃɂ����
�Ƃ������͂̍S�����������݂��Ă�����̂ƍl���邱�Ƃ��ł���B![]() ��
��łȂ����Ƃɂ͏\�����ӂ���K�v������B
��
��łȂ����Ƃɂ͏\�����ӂ���K�v������B
���Ȃ݂Ɏ�(3.42)��Hooke�̖@�����C�Ђ��݂�^����
���Ƃ��ď��������C��(3.44)�Œ�`����Young��
��Poisson���p�����
�Ƃ��������Ƃ��ł���B
���ʂЂ��ݏ�Ԃł�
![]() �Ȃ̂ŁC
���̎��������(3.110)�����߂邱�Ƃ��ł���B
�Ȃ��C���ʂЂ��ݏ�̕��ʓ��̒e���W���͓����ʓ���3�����̂����
���������C�R���v���C�A���X���قȂ邱�Ƃɂ͏\�����ӂ���B
�Ȃ̂ŁC
���̎��������(3.110)�����߂邱�Ƃ��ł���B
�Ȃ��C���ʂЂ��ݏ�̕��ʓ��̒e���W���͓����ʓ���3�����̂����
���������C�R���v���C�A���X���قȂ邱�Ƃɂ͏\�����ӂ���B
�t�ɁC�|�̕������莎���̂悤�ɁC�O�͂���p���Ă��Ȃ����ʓ��m�̊Ԋu
�܂蕽�����Ђ̌�������r�I�������̂�ΏۂƂ���ꍇ�C
���̌���������![]() �����Ƃ�ƁC����2�����ɔ�ׂ�
�����Ƃ�ƁC����2�����ɔ�ׂ�![]() ������
���͂�����قǑ傫���͂Ȃ�Ȃ����낤�Ƃ������Ƃ͗e�Ղɗ\�z�ł���B
���������āC���́i�����ɂ͋N���蓾�Ȃ��j�ߎ��Ƃ���
���͏�Ԃ����ʓI�ł���悤��
�ꍇ���l���C���ʉ���
��ԂƌĂԁB���̏��������͐����ŕ\����
������
���͂�����قǑ傫���͂Ȃ�Ȃ����낤�Ƃ������Ƃ͗e�Ղɗ\�z�ł���B
���������āC���́i�����ɂ͋N���蓾�Ȃ��j�ߎ��Ƃ���
���͏�Ԃ����ʓI�ł���悤��
�ꍇ���l���C���ʉ���
��ԂƌĂԁB���̏��������͐����ŕ\����
�ƂȂ�B�������(3.42)�ɑ�������
�Ƃ������������̂ŁC![]() -
-![]() �ʓ��ł̍\���W��
�ʓ��ł̍\���W��
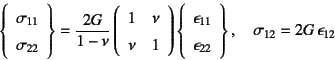 |
(3.113) |
(3.114)
�ƂȂ�B
���̊W��p����C�ʊO�̏�������
(3.115)
�ƂȂ�B���ʂЂ��݂̏ꍇ�Ɠ��l�C��(3.111)��
���ʉ��͂̍S��������(3.112)�������Ă��C�����W��
���邱�Ƃ��ł���B
���̎�(3.115)���邢�͏�̎�(![]() )�́C�ʊO�Ђ��݂ւ�
�S�������Ƒ����邱�Ƃ��ł��C���������Ӗ��ł������ɐݒ�ł����ԂƂ�
�l������߁C�ߎ��I�ȏ�Ԃł���ƍl���Ȃ���Ȃ�Ȃ��B
�Ȃ��C���ʉ��͏�̕��ʓ��̃R���v���C�A���X�͓����ʓ���3�����̂����
���������C�e���W���͈قȂ邱�Ƃɂ͏\�����ӂ���B
)�́C�ʊO�Ђ��݂ւ�
�S�������Ƒ����邱�Ƃ��ł��C���������Ӗ��ł������ɐݒ�ł����ԂƂ�
�l������߁C�ߎ��I�ȏ�Ԃł���ƍl���Ȃ���Ȃ�Ȃ��B
�Ȃ��C���ʉ��͏�̕��ʓ��̃R���v���C�A���X�͓����ʓ���3�����̂����
���������C�e���W���͈قȂ邱�Ƃɂ͏\�����ӂ���B
�܂��C�����C�Ⴆ��![]() �����ւ̍|�̈����莎���̂悤�ɁC
�قډ��͂�
�����ւ̍|�̈����莎���̂悤�ɁC
�قډ��͂�![]() �݂̂�1����ԂɂȂ��Ă���ꍇ�ɂ́C
���̎�(3.114)����
�݂̂�1����ԂɂȂ��Ă���ꍇ�ɂ́C
���̎�(3.114)����
(3.116)
�Ƃ����W�ɂȂ�C�����В�����2�����ɓ\�t�����Ђ��݃Q�[�W�� �ǂ݂ƊO�͂���Young����Poisson�䂪���ڑ���ł���B ���̍Ō�̊W��(3.116a)��1������Hooke�̖@�� �ƁC���̕����ł͌ĂԂ��Ƃɂ���B
���������̎����ЂŋȂ�����������ꍇ���ɁC�C�ӓ_�̂���f���͂� �剞�͂𑪒肵�����ꍇ������B���̂悤�ȏꍇ�ɂ́C�C�ӂ�3������ �Ђ��݂��Ђ��݃Q�[�W�ő��肷��ΎO�̂Ђ��ݐ��������߂邱�Ƃ��ł��C ���ʉ��͂̉��͂Ђ��݊W�����牞�͂��Z��ł���B
����3�����̂Ђ��݂𑪒肷��Ђ��݃Q�[�W�����[�b�g�Q�[�W
������B
���[�b�g�Q�[�W�͐}-3.17�̉E�ɂ���悤��3���̂Ђ���
�Q�[�W�̑g�łł��Ă���B�߂̂��̂͐������ɑ���45�x������
��������B
�܂��}-3.17�̍��}�̂悤�ȍ��W�n���m�ł̂Ђ���
�e���\�������̕ϊ�����z�Ɏ����ƁC��(3.11)����
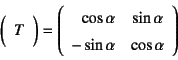
�ł��邩��C��(3.13)��
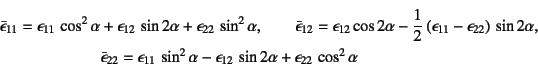
�Ə������Ƃ��ł���B�}-3.17�E��
���[�b�g�Q�[�W�̏ꍇ��![]() ��
���
��
���
![]() �̏ꍇ��
�̏ꍇ��
![]() �ɑ������邩��
�ɑ������邩��
�ƂȂ�B�������
![]() ,
,
![]() �ł��邩��C
���ǂ��̑���_�̂���f�Ђ��ݐ�����
�ł��邩��C
���ǂ��̑���_�̂���f�Ђ��ݐ�����
�Ɠ���B����ɁC��Ђ��ݕ����i�剞�͕����������j�́C���
�Ђ��ݐ����Ԃ̍��W�ϊ���
![]() �ɂȂ�����ł��邱�Ƃ���
�ɂȂ�����ł��邱�Ƃ���
�Ō��܂����![]() �ł���B
�ł���B
�܂����Ђł��邱�Ƃ��畽�ʉ��͏�Ƌߎ��ł��C��(3.114)��
�t�W����
�Ƃ����W�ɂȂ�B�剞�͕����͎�Ђ��ݕ����Ɠ����ł���C
�剞�͎͂�(3.29)�̉�
�ɂȂ�B���̕������Ƃ������̂�i=I�ł���C���̕����̏ꍇ��i=II�ł���B
�Ƃ���ŏ�̍��W�ϊ�����
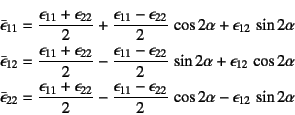
�Ƃ��������Ƃ��ł���B����������
�ƒ�`���Ă����ƁC��̊W��
| (3.118) |
�Ƃ����W������B
���̎��́C��1����
![]() ��
��
![]() ��
�u�������Ă����l�ɐ�������B
���̊W��}�������̂��}-3.18�ł���B
�܂�C�C�ӓ_�̐L�тЂ��ݐ����Ƃ���f�Ђ��ݐ����Ƃ̊W��
�}�������悤�ȉ~���2�_�Ŏw��ł��Ă���B
�܂��C�����Ɖ~�Ƃ̌�_�����ꂼ���Ђ��݂ɂȂ��Ă���
���Ƃ́C
��
�u�������Ă����l�ɐ�������B
���̊W��}�������̂��}-3.18�ł���B
�܂�C�C�ӓ_�̐L�тЂ��ݐ����Ƃ���f�Ђ��ݐ����Ƃ̊W��
�}�������悤�ȉ~���2�_�Ŏw��ł��Ă���B
�܂��C�����Ɖ~�Ƃ̌�_�����ꂼ���Ђ��݂ɂȂ��Ă���
���Ƃ́C
![]() �ɂȂ������
�ɂȂ������
![]() �Ƃ��āC
���̂Ƃ���
�Ƃ��āC
���̂Ƃ���
![]() ,
,
![]() �����ꂼ��
��Ђ���
�����ꂼ��
��Ђ���
![]() ,
,
![]() �ł��邱�Ƃ��㎮�ɑ������
���邱�Ƃ��ł���
�ł��邱�Ƃ��㎮�ɑ������
���邱�Ƃ��ł���
![]() ,
,
![]() �Ƃ���
�W��������炩�ł���B
���̂悤�ȉ~��Mohr�̂Ђ��݉~
�ƌĂԁB���͂ɂ��Ă����l�̉~���`����B
�Ƃ���
�W��������炩�ł���B
���̂悤�ȉ~��Mohr�̂Ђ��݉~
�ƌĂԁB���͂ɂ��Ă����l�̉~���`����B
��-8�ŏЉ�镽���_�ł́C�̊g�����
��ׂČ��������ɔ������Ƃ�O��ɂ��Ă��邽�߁C���̍\�����ɂ�
���ʉ��͖��̂��ꂪ�p������B���ہC�|�\���ł���C
���̂悤�ȋߎ��͋��e�ł������ł���B
�܂��C�}-3.19�̂悤�ȑ@�ە⋭��
�łł��������̕����C���̑@�ۂ̌��������ɈقȂ�悤��
�w��ɏd�˂Đϑw��
�����C�����⋭�⋴�����̂Ɏg�����Ƃ�����B
�����̓|���}�[�ɃK���X�@��(GFRP)��Y�f�@��(CFRP)��
�z�����Ă���B���̔����ʉ��͖��̍\�������p�����C
��(3.114)����ʉ�����
�ƕ\����邱�Ƃ������B
������![]() ,
, ![]() ��2������Young���ŁC
��2������Young���ŁC![]() ,
, ![]() ��Poisson��C
�����
��Poisson��C
�����![]() ���̖ʓ��̂���f�e���W��
���̖ʓ��̂���f�e���W��
�ł���B���������āC���̔̓Ɨ��ȍޗ��萔�͌܂i
![]() �̏ꍇ�j
�Ȃ����l�i
�̏ꍇ�j
�Ȃ����l�i
![]() �̏ꍇ�j�ɂȂ�B
���邢�͋t�W��
�̏ꍇ�j�ɂȂ�B
���邢�͋t�W��
�Ə������Ƃ��ł���B
�����ŁC3�����̒e���e���\���Ƃ��̐ϑw�̍ޗ��萔�Ƃ̊W�����߂Ă������B
����f�ɂ��Ă͎�(3.120)��
�����̂ŁCYoung����Poisson��ɂ��Ă݈̂ȉ��ŋ��߂�B
�܂�![]() �����̉��͂���ɂȂ�悤�ȕ��ʉ��͏�Ԃɂ�����̂Ƃ���ƁC
��(3.61)����
�����̉��͂���ɂȂ�悤�ȕ��ʉ��͏�Ԃɂ�����̂Ƃ���ƁC
��(3.61)����
����������B
����𑼂̓�̒����͂ƐL�тЂ��݊Ԃ̊W���ɑ�����Đ��������
��B
���̋t�W�����߂Ď�(3.119)��
��r���邱�Ƃɂ����
�Ƌ��߂���B
�Ⴆ�C�����⋭�@�ۂ̓����d�l��![]() ������
������![]() �����ɒ�������
�z�u����Ă���ꍇ�ɂ́C����2�����̍ޗ������������ɂȂ邽��
�����ɒ�������
�z�u����Ă���ꍇ�ɂ́C����2�����̍ޗ������������ɂȂ邽��
����������ޗ��Ƒ�������B
���̂Ƃ���(3.121)����
�ƂȂ�C�e���e���\���͑Ώ̂ɂȂ�B �Ȃ����R�ł��邪�C���ʉ��͏�̖ʓ��̃R���v���C�A���X�́C3�����̂���C �܂莮(3.70)�`��(3.72)�ƈ�v����B
�Ō�ɐ}-3.19�̂悤�ɁC1��ނ�
�@�ۂ�![]() ����������ɂ��ĕ���ł���@�ە⋭�̏ꍇ�ɂ́C
�ޗ���3�����I�ɂ�
����������ɂ��ĕ���ł���@�ە⋭�̏ꍇ�ɂ́C
�ޗ���3�����I�ɂ�![]() ������
������![]() �����������ޗ������������C
�����������ޗ������������C![]() ����
�Ώ̎��Ƃ��鉡�����ޗ��Ƃ��đ����邱�Ƃ��ł���B
���������āC��(3.63)�̓Y����(
����
�Ώ̎��Ƃ��鉡�����ޗ��Ƃ��đ����邱�Ƃ��ł���B
���������āC��(3.63)�̓Y����(![]() )��(
)��(![]() )��
���u����������̂ŁC3�����̍ޗ��萔��
)��
���u����������̂ŁC3�����̍ޗ��萔��
�̂����Z�i
![]() �̏ꍇ�j�Ȃ���
�܂i
�̏ꍇ�j�Ȃ���
�܂i![]() �̏ꍇ�j���Ɨ��Ȓ萔�ɂȂ�B
���̏ꍇ�ɂ͎�(3.121)����
�̏ꍇ�j���Ɨ��Ȓ萔�ɂȂ�B
���̏ꍇ�ɂ͎�(3.121)����
�ƂȂ�B�}�Ɏ������悤�ȑ@�ۂ̔����\����C��ʂɂ�
![]() ��
�l����̂��f���ł��邪�C���̂悤�ȑ@�ە⋭�ł́i�ƂĂ��s�v�c�Ȃ��Ƃ�
�G�l���M���x�������݂��āj�C�e���e���\���͑Ώ�
��
�l����̂��f���ł��邪�C���̂悤�ȑ@�ە⋭�ł́i�ƂĂ��s�v�c�Ȃ��Ƃ�
�G�l���M���x�������݂��āj�C�e���e���\���͑Ώ�![]() �����
�����
�ɂȂ�B
�����̕����ł͑Ώ̐��i![]() �j���ŏ����牼�肵�Ă���3.24�̂Œ��ӂ���B
�Ȃ����R�ł��邪�C���ʉ��͏�̖ʓ��̃R���v���C�A���X�́C3�����̂���C
�܂莮(3.66)�`
��(3.68)�ƈ�v����B
�j���ŏ����牼�肵�Ă���3.24�̂Œ��ӂ���B
�Ȃ����R�ł��邪�C���ʉ��͏�̖ʓ��̃R���v���C�A���X�́C3�����̂���C
�܂莮(3.66)�`
��(3.68)�ƈ�v����B
�O�߂ŗU��������̕��ʖ��́C���͊������邱�Ƃɂ����
��͓I�ɉ������Ƃ��ł���B������̖����`���I�ɂ�![]() -
-![]() ��
���̖��Ƃ��ĕ��Ă���C���̌��ʂ�p����
��
���̖��Ƃ��ĕ��Ă���C���̌��ʂ�p����![]() �����̔��Ȑ�����
�Z�肪�t�ѓI�ɂł���B���̕��ʓ��̉��͂Ђ��݊W�́C���̂悤�ɂ�
�\�����Ƃ��ł���B
�����̔��Ȑ�����
�Z�肪�t�ѓI�ɂł���B���̕��ʓ��̉��͂Ђ��݊W�́C���̂悤�ɂ�
�\�����Ƃ��ł���B
������
�ƒ�`�iNorthwestern��wDundurs������`Elasticity'�� �u�`�m�[�g�i1980�N���j���j�����B
���̊W����(3.17)��2�����ł̂Ђ��݂�
�K���������ɑ�����C�荇�������l�������
�ƂȂ�B��������͂ŕ\�����K���������ƌĂԁB
����ɁC���z�O�͂����炩�̃|�e���V������![]() ��
�\���ł���Ɖ��肵
��
�\���ł���Ɖ��肵
�ƒu������̂Ƃ���C�㎮(3.125)��
�ƂȂ�B
���āC���������![]() �ɂ����
�ɂ����
�̂悤�ɉ��͂�\�����Ƃ��ł����Ƃ���ƁC����͎���
���͂̂荇����(3.21)�������I�ɖ�������B
���������āC���������������ɑ���![]() �����߂邱�Ƃ��ł����
���͂��킩��C��(3.123)����Ђ��݂����߂���B
�����
�����߂邱�Ƃ��ł����
���͂��킩��C��(3.123)����Ђ��݂����߂���B
�����![]() ���Ђ��݂̓K��������(3.126)������悤��
�Ȃ��Ă���Ύ�(3.6)�̂Ђ��ݕψʊW�͐ϕ��ł��C
�C�ӓ_�̕ψʂ��Z��ł���B
���������āC�ŏI�I�ɗB��̉������߂��邽�߂ɂ́C
��(3.127)�ŕ\����鉞�͂��Ђ��݂̓K��������(3.126)��
����������K�v������B��������������
���Ђ��݂̓K��������(3.126)������悤��
�Ȃ��Ă���Ύ�(3.6)�̂Ђ��ݕψʊW�͐ϕ��ł��C
�C�ӓ_�̕ψʂ��Z��ł���B
���������āC�ŏI�I�ɗB��̉������߂��邽�߂ɂ́C
��(3.127)�ŕ\����鉞�͂��Ђ��݂̓K��������(3.126)��
����������K�v������B��������������
��B���Ȃ킿�C���̎�(3.128)������悤��
��![]() �����߂邱�Ƃ��ł���C�ő̂̕��ʖ��͉��������ƂɂȂ�B
���̊�
�����߂邱�Ƃ��ł���C�ő̂̕��ʖ��͉��������ƂɂȂ�B
���̊�![]() ��Airy�̉��͊�
�ƌĂ�ł���B
���z�O�͂������ꍇ�ɂ́C�㎮(3.128)��
��Airy�̉��͊�
�ƌĂ�ł���B
���z�O�͂������ꍇ�ɂ́C�㎮(3.128)��
| (3.129) |
�ƂȂ�B�܂�C���͊����d���a�� �ł���B �d���a���͔��ɑ������݂��C�ł��ȒP�Ȃ��̂͑������ł���B
�����ł͑������ʼn��͊����\���ł���悤�ȗ���
����[74]������グ��B
�������Ζ��炩�Ȃ悤��
�͏㎮�����Ă���B![]() �Ƃ���Ƃ���(3.127)��
�������ƔC�ӓ_�̉��͂��Z��ł���B
������̑����������ł��邪�C������
�������̂͐}-3.20�ɂ���悤�ȒP���x�����ꂽ
�̉��͂�^����\�������镔�������𒊏o�������̂ł���B
���̖��̋��E������
�Ƃ���Ƃ���(3.127)��
�������ƔC�ӓ_�̉��͂��Z��ł���B
������̑����������ł��邪�C������
�������̂͐}-3.20�ɂ���悤�ȒP���x�����ꂽ
�̉��͂�^����\�������镔�������𒊏o�������̂ł���B
���̖��̋��E������
����сC�{����![]() ��
��![]() �Ƃ������Ƃ��낾���C
���������
�Ƃ������Ƃ��낾���C
���������![]() �����߂邱�Ƃ͍���Ȃ̂ŁC�����ɂ߂�
�����߂邱�Ƃ͍���Ȃ̂ŁC�����ɂ߂�
�̂悤�ɕ��ϓI�ɗ͂ƃ��[�����g����p���Ă��Ȃ����̂ɂ��Ă������B
�ȏ�̋��E������![]() ��������ƁC�e�W����
��������ƁC�e�W����
�ƌ���ł���B�����������C���͕��z��
�Ƌ��߂���B���͐���![]() �̑�1���͎��͂Œ莮������
���������_�̉��ł���C��2����
�̑�1���͎��͂Œ莮������
���������_�̉��ł���C��2����
![]() ��2��ɔ�Ⴕ��
�������Ȃ�B���Ȃ킿�ג������ł���Α�2���͖����ł���ق�
�������Ȃ�B
������̒�����
��2��ɔ�Ⴕ��
�������Ȃ�B���Ȃ킿�ג������ł���Α�2���͖����ł���ق�
�������Ȃ�B
������̒�����![]() �̑傫�������l�ɁC
�̑傫�������l�ɁC![]() ��
��r�����Ƃ�
��
��r�����Ƃ�
![]() ��2��ɔ�Ⴕ��
�������Ȃ邱�Ƃ��������Ƃ��ł���B
�܂�����f����
��2��ɔ�Ⴕ��
�������Ȃ邱�Ƃ��������Ƃ��ł���B
�܂�����f����![]() �͕��������z���Ă���C�����
���͂Œ莮�����闝�_�ŋ��߂�����̂ɓ������B
�͕��������z���Ă���C�����
���͂Œ莮�����闝�_�ŋ��߂�����̂ɓ������B
��������(3.130)�Ŏ������悤�ɁC
�[��![]() �̋��E�����͌����Ȃ��̂ł͂Ȃ����ϓI�Ȃ��̂Ƃ���
�^�����B���̂��߁C���ʓI�ɂ͐}-3.21�ɂ���悤��
����
�̋��E�����͌����Ȃ��̂ł͂Ȃ����ϓI�Ȃ��̂Ƃ���
�^�����B���̂��߁C���ʓI�ɂ͐}-3.21�ɂ���悤��
����![]() �����E�[�ɂ͕��z���Ă����肪��������
�߂��Ȃ��B�������C�\���͊w�Ƃ��Ă̋��E�����Ƃ��āC
���͂ƋȂ����[�����g����ɂȂ��������(3.130)��
�������Ă���B�܂��C�\���͊w�̑ΏۂƂȂ�悤�ȍג����_��
�ꍇ�ɂ́C���̒[���̕��z�����ΓI�ɏ��������̂ɂȂ�B
�����Saint-Venant�̌���
�ɂ���āC���ۂɂ͒[������̋����������Η����قǂ��̒[���̉e����
�������Ȃ邱�Ƃ��킩���Ă���B
��(3.131)�̋�̓I�ȕ��z
�}�́C�t�^-B�̐}-B.4��
�L���v�f���Ƌ��Ɏ������B
�ŏI�I�ɏ�̉��͕��z����(3.123)�ɑ�����C
�������(3.6)�ɑ�����Đϕ�����C
�K�ȋ��E�����̂��Ƃŕψʐ���������ł���B���͊�
�����E�[�ɂ͕��z���Ă����肪��������
�߂��Ȃ��B�������C�\���͊w�Ƃ��Ă̋��E�����Ƃ��āC
���͂ƋȂ����[�����g����ɂȂ��������(3.130)��
�������Ă���B�܂��C�\���͊w�̑ΏۂƂȂ�悤�ȍג����_��
�ꍇ�ɂ́C���̒[���̕��z�����ΓI�ɏ��������̂ɂȂ�B
�����Saint-Venant�̌���
�ɂ���āC���ۂɂ͒[������̋����������Η����قǂ��̒[���̉e����
�������Ȃ邱�Ƃ��킩���Ă���B
��(3.131)�̋�̓I�ȕ��z
�}�́C�t�^-B�̐}-B.4��
�L���v�f���Ƌ��Ɏ������B
�ŏI�I�ɏ�̉��͕��z����(3.123)�ɑ�����C
�������(3.6)�ɑ�����Đϕ�����C
�K�ȋ��E�����̂��Ƃŕψʐ���������ł���B���͊�![]() ��
�K������������悤�ɋ��߂��Ă���̂ŁC���̐ϕ��͗B���
�ψʐ�����^����͂����B
���ʂɂ��Ă͕���[74]���Q�Ƃ̂��ƁB
��
�K������������悤�ɋ��߂��Ă���̂ŁC���̐ϕ��͗B���
�ψʐ�����^����͂����B
���ʂɂ��Ă͕���[74]���Q�Ƃ̂��ƁB
������̗�Ƃ��āC�ɍ��W�n�ɂ�����Airy�̉��͊������グ�悤�B
������Northwestern��wDundurs������`Elasticity'��
�u�`�m�[�g�i1980�N���j������p�����B
�Ƃ������͊������
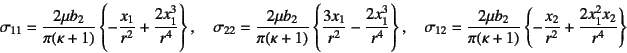
�Ƃ��������͕��z�����߂���B
����ɑΉ�����ψʏ�ɂ́C�}-3.22��
�������悤�ɁC![]() �̕�����
�̕�����![]() �����̃M���b�v������B
����͐}-A.1�Ɏ������]�ʂ̐}���v����90�x��]������
��\���Ă��邱�Ƃ���C�㎮�̉��͊���
�����̃M���b�v������B
����͐}-A.1�Ɏ������]�ʂ̐}���v����90�x��]������
��\���Ă��邱�Ƃ���C�㎮�̉��͊���![]() ��1�����w�I�]��
�����݂����̉���^����ƍl�����Ă���B
����������
��1�����w�I�]��
�����݂����̉���^����ƍl�����Ă���B
����������
![]() �͓]�ʂ̂���C
�܂茋���i�q��ʕ��̌�����\���Ă���CBurgers�x�N�g��
�ƌĂ�Ă���B
�M���b�v��
�͓]�ʂ̂���C
�܂茋���i�q��ʕ��̌�����\���Ă���CBurgers�x�N�g��
�ƌĂ�Ă���B
�M���b�v��![]() �̕������ł��邱�Ƃ���
�̕������ł��邱�Ƃ���![]() �̂悤�ɕ��ɂ��Ă���B
�㎮�̉��͂̂����C
�̂悤�ɕ��ɂ��Ă���B
�㎮�̉��͂̂����C![]() ��
��![]() ��
��![]() �ł̒l�����߂��
�ł̒l�����߂��
�ƂȂ�B
�����ŁC���̓]�ʂ�![]() ����ɓK�ɕ��ׂ邱�Ƃɂ���āC�T���
���f�������Ă݂悤�B�܂�C�}-3.23�̂悤�ɁC
�Ⴆ��4�̓]�ʂ�2����
�t�����Ɉ��ɕ��ׂ�ƁC�M���b�v��
����ɓK�ɕ��ׂ邱�Ƃɂ���āC�T���
���f�������Ă݂悤�B�܂�C�}-3.23�̂悤�ɁC
�Ⴆ��4�̓]�ʂ�2����
�t�����Ɉ��ɕ��ׂ�ƁC�M���b�v��![]() ��������E��
��������E��

�ƌv�Z���Ă��������̂ŁC���E�[�̓]�ʂ̈ʒu�ł̓M���b�v�͕���B
����ŁC���̒����̋T������f�����ł������ƂɂȂ邾�낤�B
�����ŁC������![]() �̋T��1�������݂���C�����ɑ傫���̈��
��l�ȉ���
�̋T��1�������݂���C�����ɑ傫���̈��
��l�ȉ���![]() �ň��������ꍇ�̖����C�]�ʂ�
�ň��������ꍇ�̖����C�]�ʂ�
![]() ��
�K�ɕ��ׂ邱�Ƃɂ���ĉ����Ă݂悤�B���Ȃ݂ɁC
��
�K�ɕ��ׂ邱�Ƃɂ���ĉ����Ă݂悤�B���Ȃ݂ɁC![]() �����
�C�ӂ̓_
�����
�C�ӂ̓_![]() �ɓ]�ʂ�1����ꍇ�́C���̎����
����
�ɓ]�ʂ�1����ꍇ�́C���̎����
����![]() �́C�㎮�̌��_���ړ������������
�́C�㎮�̌��_���ړ������������
�ł���B
������
![]() �ɕ��ׂ�]�ʂ̕��z��
�ɕ��ׂ�]�ʂ̕��z��![]() �Ƃ���ƁC
�㎮��
�Ƃ���ƁC
�㎮��![]() ��
��![]() �Œu�������ďd�ˍ��킹���������C
�Œu�������ďd�ˍ��킹���������C![]() �����
����
�����
����
![]() ��
��
�ƂȂ�B�܂�
![]() �̊Ԃ̃M���b�v��
��̎�(
�̊Ԃ̃M���b�v��
��̎�(![]() )���g������
)���g������
�ƂȂ�B���������āC����
![]() �̕������T��ł���
�����́C���������R�\�ʂ�
�̕������T��ł���
�����́C���������R�\�ʂ�![]() ��
��![]() ����ɂȂ�C
�M���b�v�͗��[�ŕ��Ă��邱�ƂɂȂ�B
�܂�C
����ɂȂ�C
�M���b�v�͗��[�ŕ��Ă��邱�ƂɂȂ�B
�܂�C![]() ��
��![]() �����̏����ɂȂ�B�����
�����̏����ɂȂ�B�����
�ł���������ƂɂȂ�B�ŏ��̎��́C
![]() �Ƃ���
���ق��j�����C
��1���Cauchy�̓����ϕ�������
�ƌĂ��B
�܂�C���m��
�Ƃ���
���ق��j�����C
��1���Cauchy�̓����ϕ�������
�ƌĂ��B
�܂�C���m��![]() �̉��炩�̐ϕ����C�E�ӂ�
����^����ꂽ���ɂȂ�悤�ɁC
�̉��炩�̐ϕ����C�E�ӂ�
����^����ꂽ���ɂȂ�悤�ɁC![]() �����߂Ȃ���Ȃ�Ȃ��B
�����āC��Ԗڂ̎��͂��̖��m���ɑ��鐧������ł���B
�ϕ��������̉������ɂ��ẮC���̂悤�Ȍ���������B
�����߂Ȃ���Ȃ�Ȃ��B
�����āC��Ԗڂ̎��͂��̖��m���ɑ��鐧������ł���B
�ϕ��������̉������ɂ��ẮC���̂悤�Ȍ���������B
��1���Cauchy�̓��ِϕ��������Ɋւ������: ���̐ϕ�������
�̉���
�ƂȂ�B�������͓�������
�͒萔�ł���B
�ŗL�E�� �������݂��邽�߂ɂ́C���̓K������
���������Ȃ���Ȃ�Ȃ��B�����ē�������

�ƂȂ�B
����܂��āC���i������������������![]() ��
�L�����ꍇ�j��������
��
�L�����ꍇ�j��������
![]() ��
��
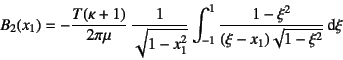
�ƂȂ�̂ŁC�ŏI�I��
![]() �̕���������
�̕���������
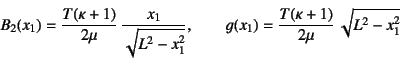
�Ƌ��߂���B�܂�C�]�ʕ��z�͋T�����[�Ŗ�����̒l�������C
�T��͊J���Ƒȉ~�`�ɂȂ邱�Ƃ������Ă���B
���̂Ƃ���![]() ����̉��͂����߂�ƁC
�������
����̉��͂����߂�ƁC
�������
![]() ��
��
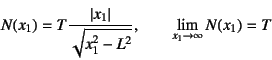
�ƂȂ�B�T�牓�������i![]() �j�ƈ�l��
�O��
�j�ƈ�l��
�O��![]() �Ɠ������Ȃ�B
�Ɠ������Ȃ�B
����C���̉��͂̋T����[�i![]() ;
; ![]() �j�t�߂ł�
�l�����߂Ă݂��
�j�t�߂ł�
�l�����߂Ă݂��
| (3.132) |
�ƂȂ�C�T����[����̋����̕������̓��ِ��������Ă��邱�Ƃ��킩��B
������![]() �͔j�[�hI�����͊g��W��
�ƌĂ����̂ŁC�j��͊w�̊�{�I�ȃp�����[�^�ł���B
�ł���{�I�Ȕj��K���́C���̉��͊g��W�����j���Ր�
�ƌĂ���l
�͔j�[�hI�����͊g��W��
�ƌĂ����̂ŁC�j��͊w�̊�{�I�ȃp�����[�^�ł���B
�ł���{�I�Ȕj��K���́C���̉��͊g��W�����j���Ր�
�ƌĂ���l![]() �ɒB�����Ƃ��ɋT�i�W����Ƃ��Ă���B
�ǎ҂̂قƂ�ǂ��C�ϕ��������Ƃ������̂ɂ͏��߂Đڂ����Ǝv�����C
�Ⴆ�Α���̒����g�T����\�����ނ̔�j�����́C
���͐ϕ��������������Ă���i�t�^-G�Q�Ɓj�̂ł���B
�ɒB�����Ƃ��ɋT�i�W����Ƃ��Ă���B
�ǎ҂̂قƂ�ǂ��C�ϕ��������Ƃ������̂ɂ͏��߂Đڂ����Ǝv�����C
�Ⴆ�Α���̒����g�T����\�����ނ̔�j�����́C
���͐ϕ��������������Ă���i�t�^-G�Q�Ɓj�̂ł���B