最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
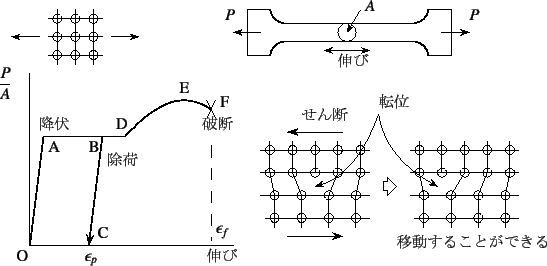
材料特性を調べるためにはいろいろな材料試験を行う。図-A.1の 右上にあるような棒（平板か円柱）を一方向に引張る試験はその代表である。 左下に示したのが，荷重を棒の載荷前の断面積で割った応力と 棒の伸びをプロットしたもので，鋼の場合の例である。 このプロットが示す特性から材料特性を同定することができる。
剛性は，図-A.1のような材料の抵抗特性はもちろん， 構造の見かけ上の抵抗特性を表した抵抗曲線の， 任意の変形状態における接線係数すべてを表す概念であり， 変形のし難さを表す特性である。 最も基本的な剛性は弾性的な抵抗の程度， つまり，図-A.1のO-A部分の傾きで定量化できる。 鋼のような金属の結晶材料の場合は，左上の図のように 強い原子間力で抵抗することから，コンクリート等の他の 材料に比べてその傾きは非常に大きい。 抵抗が大きいこのような材料は普通の人達には「強い」ものと感じ， そのように表現することがあるが，後述の「強度」とは違う概念である。 また「硬い」という特性とも厳密には異なるので，我々技術に関係する者は 十分に注意する必要がある。
分子が整然と並んでいれば，その間の抵抗力が非常に大きいので， 破断する応力は非常に大きいと想像できるが， 実際には図-A.1の点Aあたりで急に抵抗が小さくなるのが 普通である。この点A付近で発生している現象を降伏と呼び， 点Aの応力レベルを降伏応力 と呼んでA.1いる。
このようなメカニズムを表す一つの簡単なモデルは，
図の右側に書いたような転位
の移動と蓄積である。
材料を造るときには結晶の格子構造のすべてを完全には並べることができず，
この図のような転位と呼ばれる欠陥が多数含まれてしまう。
このような，きちんと握手していない格子の配置が，
この図の奥行き方向に有限な長さで曲線状に存在してしまう。
この欠陥はそれほど大きくない力（せん断力A.2）で移動し，逆向きに力をかけると逆向きに
移動する。しかし，転位が単結晶の境界（界面）A.3や
材料の表面に達すると，
そこで動けなくなるため，力を抜いても元には戻らない。
そのため，内部に残留変形が生じることになる。
例えば点Aから点Bまでの間に多くの転位が表面や界面に
移動するので，点Bで荷重をかけるのをやめて除荷しても，点Aの方向に伸びが
戻るのではなく，点Cの方向に伸びが戻る。そのため，全荷重を抜いた
状態でも，残留変形
が生じることになる。
そしてこの残留変形は時間が経っても変化しない。
このような非可逆変形を塑性変形
と呼んでいる。
その後荷重を増やし続けると，点Dで再度抵抗が大きくなる。 これは，単結晶界面等に転位が蓄積して動けなくなることによって硬くなるような， 塑性的な硬さが増す性質に相当し，弾性剛性とは異なる。 このD-E付近の曲線の傾きがA-D付近のそれよりも大きく（硬く）なることを 硬化と呼んでいる。 「硬さ」あるいは「硬度」と呼ばれている性質は，Vickersの硬さ試験 等で確認される特性であり，押し付けた角錐形の治具が材料に残す塑性変形の 大小を測定して評価する。 したがって，塑性硬化の程度を主として，降伏応力の大小も 含めた総合的な特性が「硬さ」と呼ばれている。
さらに荷重を増やすと，点Eのような最高荷重に達し，その後 軟化して点Fで破断する。この点Eや点Fの応力レベルを強度と呼ぶ。 ただし図の縦軸は，試験片を引張る前の断面積で荷重を除して定義していることに 注意しないといけない。それは，点E付近で試験片の実際の断面積は 小さくなり始めるからである。このような現象を「絞り 」と呼ぶこともあるが， この小さくなった断面積で荷重を除した応力を定義すると， 点Eのようなピークは発生せず，点Fは点Eよりも高いレベルになる。 そのため，変形状態のそれぞれのレベルでの断面積で荷重を除した 応力（真応力） によって求められる破断応力を強度とするのが正確であろう。
最終的に破断するまでに，どのくらいまで伸びることができるのか
表したのが延性である。図の量の中では，破断時の伸び
の
大きさの程度が延性である。
ただし，この破断は常温で亀裂の無い試験片を引張ったときに
起こる破壊であり，
通常の鋼では大きな変形を伴いながら破壊する延性破壊
である。
これに対し，亀裂
を入れた同じ材料を，亀裂が進展するように荷重を加えたときの，
亀裂の進行部分での伸びの程度，つまりは微視的な延性は，必ずしも
上述の延性と同じとは限らない。特に温度が低くなると亀裂付近の
微視的な延性は小さくなる。
そのような微視的な延性が小さい材料はガラスのように脆いことがある。 微視的な延性が小さいために少ない変形で亀裂が進展して，最終的に 亀裂が試験片の表面まで達した段階で破断が生じるため， 全体的にも小さい変形のままで破断することになる。 このような脆さを脆性と呼ぶ。 そして，このような脆性破壊 を起こすのに多くのエネルギが必要な材料は，靭性が高い材料と呼ばれる。 すなわち，脆性破壊に必要な破壊エネルギの程度で靭性を表す。 具体的には，溶接接合部等にあってはならない初期欠陥から， 低いレベルだが繰り返し作用する外力に対して徐々に 亀裂が進展して破壊に至る疲労 破壊に対する強度を表現するために必要な性質である。
簡単な表現をすると，亀裂の進展を伴う破壊に対する「粘り強さ」が靭性である。 このことから，靭性と前節の延性とは直接には関連していないことが明らかであり， 注意が必要である。あくまでも亀裂付近の微視的な延性が脆性や靭性と 直接関係しているのである。 また靭性を定量化するためのCharpy衝撃試験 が動的な載荷によって行われるため， 靭性を衝撃への抵抗性とする記述が時折見られる[123]が， それも間違いである。 また小さい変形のまま衝撃的に破壊する性質を脆性とする記述もあり， 前半は微視的な延性が小さいことを指すため正しい表現であるが，後半は 不安定な亀裂進展による動的な破壊を主観的に記述したものであり， あまりいい表現ではない。 脆性が問題視されるきっかけになった船舶の沈没は，凪いでとても静かな 海上で起きた[7]ことを覚えておこう。 このように，塑性変形を伴いながら 延性破断するまでの伸びの大きさ（荷重伸び曲線の伸び方向の大小）で 延性が定義されるのに対し， 靭性は脆性破壊までに必要なエネルギあるいは塑性仕事の大きさ（荷重伸び 曲線の破断までの経路と横軸で囲まれた面積の大小；正確ではないが）で 定義される特性[72]である。
地震工学の分野では，地震エネルギを構造物が散逸させる性質に関連して 「靭性率」や「靭性レベル」といった用語を使うことがある。 エネルギ的な抵抗能力なので本来は`toughness'とすべきだが， その英訳には延性を示す英語`ductility'を用いている。 すなわち，構造物が大きな塑性変形を伴いながら，入力された地震エネルギを 消費する性質を指した用語であるため，「塑性率」といった表現の方が 適切とも考えられる。ただ除荷曲線が弾性挙動と同じであるという前提に 立てば，高い`ductility'はエネルギ的あるいは塑性仕事的な 大きな散逸効果と等価になるため，靭性の方が比較的正しい表現であろう。 つまり，靭性という用語の地震工学分野での用いられ方が， 分野を越えた基礎科学である材料力学での歴史のある長年の 慣習には従っていないことには留意しておこう。 文献[116]の「靭性率」の 項目を見ると，材料特性としては`toughness rate'と英訳されているが， 塑性的終局強度特性としては`ultimate ductility factor'となっており， やはり統一がとれていない。
