 |
最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
ここでは主桁を設計するときの,L荷重の橋軸直角(幅員)方向の載荷位置を
決定することに関して,
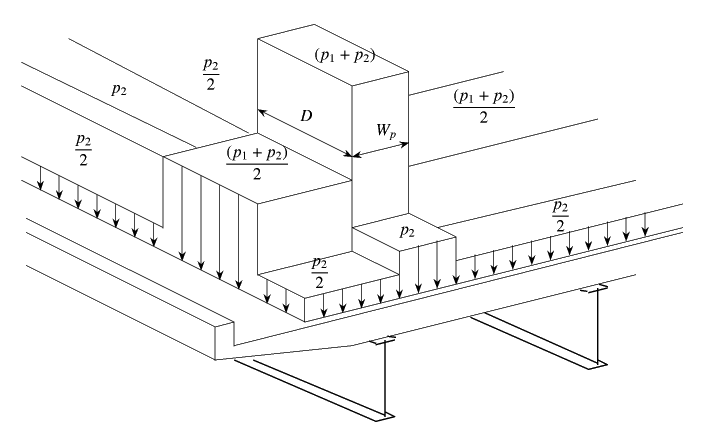
構造力学的な観点を示しておこう。図-A.2に示したのが,
現在規定されているL荷重の
分布のさせ方[128]である。図-2.19にも
示したように,橋軸方向のある長さ![]() の区間にはトラックを
想定した大きめの荷重を与えている。
橋軸直角方向にも同様に,幅
の区間にはトラックを
想定した大きめの荷重を与えている。
橋軸直角方向にも同様に,幅![]() の部分に大き目の荷重が分布するとしている。
主桁を設計する際に最初に必要なのは,
この分布をどの位置に設定するか(どこに置けば設計したい桁に
とって最も辛いのか決定する)ということである。
橋軸方向の分布位置については,
トラスを例にすれば,節-2.2.3 (3)に
例示したように影響線を用いて決定する。
その前に,設計しようとしている主桁あるいは主構に対する,
橋軸直角方向の分布のさせ方の決定,つまり
の部分に大き目の荷重が分布するとしている。
主桁を設計する際に最初に必要なのは,
この分布をどの位置に設定するか(どこに置けば設計したい桁に
とって最も辛いのか決定する)ということである。
橋軸方向の分布位置については,
トラスを例にすれば,節-2.2.3 (3)に
例示したように影響線を用いて決定する。
その前に,設計しようとしている主桁あるいは主構に対する,
橋軸直角方向の分布のさせ方の決定,つまり![]() 区間の位置決定が必要である。
ここではその考え方を示し,図-2.19の
区間の位置決定が必要である。
ここではその考え方を示し,図-2.19の![]() ,
, ![]() の
値の求め方を説明しよう。
の
値の求め方を説明しよう。
![]() や
や![]() ,
, ![]() ,
, ![]() の値については,対象とする橋梁によって異なるため,
詳細については文献[128]を参照して欲しいが,
ある種の橋梁に対しては,例えば
の値については,対象とする橋梁によって異なるため,
詳細については文献[128]を参照して欲しいが,
ある種の橋梁に対しては,例えば
のような値を用いることが規定されている。
最初は2主構トラスを例にして,橋軸直角(幅員)方向の荷重の載せ方を
考えてみよう。
トラスの場合は図-2.10に示したように,
床版の荷重が横桁を通して主構に伝達されるので,図-A.3に
示したように,二つの主構への荷重の分担は,横桁を単純梁と考えたときの
支点反力![]() ,
, ![]() の分担分と同じになる(縦桁のことは面倒なので
ちょっと忘れましょう)ことは容易に予想できると思う。
例えば左の支点反力
の分担分と同じになる(縦桁のことは面倒なので
ちょっと忘れましょう)ことは容易に予想できると思う。
例えば左の支点反力![]() の影響線は,図の三角形のようになる。
したがって,図-A.2の幅員方向の大きめの荷重を
載せる幅
の影響線は,図の三角形のようになる。
したがって,図-A.2の幅員方向の大きめの荷重を
載せる幅![]() の部分は,できるだけ左に寄せればいいことになる。
つまり図-A.3の一番下に描いたように荷重を
分布させれば,それが左側の主構にとっては最も辛い状態になる。
この
の部分は,できるだけ左に寄せればいいことになる。
つまり図-A.3の一番下に描いたように荷重を
分布させれば,それが左側の主構にとっては最も辛い状態になる。
この![]() は,
は,![]() を求める場合には
を求める場合には![]() の値を用い,
の値を用い,![]() を
求める場合には
を
求める場合には![]() とする。
とする。
具体的に![]() の場合に算定してみると,図-A.3の影響線の
網掛け部分の面積とその右の白い三角形の面積はそれぞれ
の場合に算定してみると,図-A.3の影響線の
網掛け部分の面積とその右の白い三角形の面積はそれぞれ
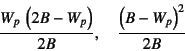
なので,荷重の総計は
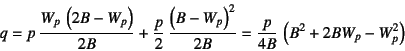
になる。したがって,例えば![]() mとして式(A.1)の
値を代入すれば,
mとして式(A.1)の
値を代入すれば,![]() kN/m,
kN/m, ![]() kN/mという値(曲げ
モーメント算定の場合)が求められる。
kN/mという値(曲げ
モーメント算定の場合)が求められる。
次に,プレートガーダの場合を考えてみよう。
近年は,初期コストや維持管理を総合した経済的な合理性から,PC床版2主桁のような
少数主桁が多用されるようになっているが,ここでは3主桁を例に用いよう。
実はプレートガーダの場合もトラスと同じように,主桁の間に
縦桁が配置される場合があり,それが支える荷重は横桁を通して主桁に
伝えられる(写真-![]() 参照)。
したがって,床版からの力の伝達は,上述のトラスのようには単純ではなくなる。
つまり,縦桁・主桁が横桁によって連結されているので,格子状になった
構造に荷重が作用することになる。
そのため,例えば片方の耳桁
と中桁
の間に単位荷重が作用した場合には,
もう片方の耳桁もある程度の荷重を分担して支えている。
しかも格子構造は不静定構造であることから,縦桁・横桁と主桁の
曲げ剛性やねじり剛性の情報が無いと,この分担率を算定することができない。
これは困ったことである。つまり,これから断面の形を設計して決めようと
している部材の剛性が,荷重を決める際にまず必要になっている。
これは矛盾ではないか。
もちろん現場では経験的な剛性比の情報の蓄積があるので,
ある程度の予測をした上で格子構造として載荷位置を決めることは可能らしい。
しかし,ここではそれを近似的に取り扱う「1-0法」を用いて,
載荷位置を決定することを示そう。
参照)。
したがって,床版からの力の伝達は,上述のトラスのようには単純ではなくなる。
つまり,縦桁・主桁が横桁によって連結されているので,格子状になった
構造に荷重が作用することになる。
そのため,例えば片方の耳桁
と中桁
の間に単位荷重が作用した場合には,
もう片方の耳桁もある程度の荷重を分担して支えている。
しかも格子構造は不静定構造であることから,縦桁・横桁と主桁の
曲げ剛性やねじり剛性の情報が無いと,この分担率を算定することができない。
これは困ったことである。つまり,これから断面の形を設計して決めようと
している部材の剛性が,荷重を決める際にまず必要になっている。
これは矛盾ではないか。
もちろん現場では経験的な剛性比の情報の蓄積があるので,
ある程度の予測をした上で格子構造として載荷位置を決めることは可能らしい。
しかし,ここではそれを近似的に取り扱う「1-0法」を用いて,
載荷位置を決定することを示そう。
では,具体的に図-A.4のような場合を対象として,
「1-0法」を説明しよう。
例えば一番上の図のように,左の耳桁と中桁の中間に単位荷重が作用している
場合に,本来は右の耳桁も何らかの分担をして支えるのであるが,
ここではそうではないとする。
つまり,例えば左の耳桁の真上に載った場合にはすべてを耳桁が支え,
中桁の真上に載った場合には,耳桁は全く分担しないものとする。
また,中桁よりも右に荷重がある場合には,左の耳桁は関与しないとするのである。
したがって,左の耳桁の分担を表す影響線は,その下の図のような三角形になり,
耳桁直上に載った場合に1の値を持つ。
さらに,その桁よりも左側には,耳桁と中桁の間の影響線をそのまま
延長する。したがって,左の耳桁よりも左に載る荷重は,
耳桁にとっては1以上の影響を及ぼすことになる。
この例では,耳桁が関与する載荷部分の幅は3.35mで![]() mよりも狭いため,
中桁より左側すべてに
mよりも狭いため,
中桁より左側すべてに![]() を載荷すれば,耳桁を設計するための
を載荷すれば,耳桁を設計するための![]() ,
, ![]() を
算定できる。具体的に計算すると,この影響線の面積は1.87mになるので,
式(A.1)の値を代入すれば,
を
算定できる。具体的に計算すると,この影響線の面積は1.87mになるので,
式(A.1)の値を代入すれば,![]() kN/m,
kN/m,
![]() kN/mという値(曲げモーメント算定の場合)が求められる。
kN/mという値(曲げモーメント算定の場合)が求められる。
次に中桁を設計する場合には,同じような考え方に基づけば,影響線は
図示したような二等辺三角形になり,中桁の真上に荷重が載ったときに1になる。
この例の場合は,耳桁間隔が6mになるので,図の影響線に網掛けした幅に![]() を
載せ,その外側に
を
載せ,その外側に![]() を載せればいいことになる。
つまり網掛けした部分の影響線面積に
を載せればいいことになる。
つまり網掛けした部分の影響線面積に![]() を乗じたものと,
その両側の小さい三角形面積に
を乗じたものと,
その両側の小さい三角形面積に![]() を乗じたものの和が設計荷重になる。
この例では前述のトラスの例と同じ幅なので,結局
を乗じたものの和が設計荷重になる。
この例では前述のトラスの例と同じ幅なので,結局![]() kN/m,
kN/m,
![]() kN/mという値(曲げモーメント算定の場合)になる。
kN/mという値(曲げモーメント算定の場合)になる。