最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。

• • • 1.2.0.0.1 桁--最も単純な橋梁形式:
    • 1.2.0.0.2 トラス--桁からウェブを無くしてしまおう:
    • 1.2.0.0.3 アーチ:

1.2 どうして力学を学ばなければならないのか

図: 最も単純な橋梁形式-- 桁けた。 牛越橋は仙台の広瀬川に架かる橋で1953年竣工
図: 牛越うしごえ橋--ゲルバー梁
図: 桁のスポンジ模型

図: 上部は圧縮で下部は引張り

社会基盤構造物（土木構造物）の一例としての橋梁を対象として， 構造物を設計（デザイン）する場合に， なぜ力学的な感覚を身に付けていないといけないのか示そう。

1.2.0.0.1 桁--最も単純な橋梁形式:

ちょうど写真-のように，谷や川等に橋梁を架ければ， 物や人・情報・文化をスムーズに渡すことができる。 最も単純な形式は桁 と呼ばれる^1.3もので

1. 橋に載っている人や車の重量は，重力下向きの力として桁にかかる。
2. 桁の中では，写真-や写真-で わかるように，上部は水平方向に縮んでいることから水平方向の圧縮で 抵抗しており，下部は伸びていることから，これも水平方向の引張りで 抵抗している。 どちらも水平方向の力で，桁の上半分と下半分で向きが逆になっている。 重量の作用は上から下への鉛直方向の力なのに，桁はそれを水平方向の 力に変換して抵抗していることは，ちょっと不思議で理解し難い。 構造力学の最初の難所である。
3. 一つの断面 （写真-と写真-の， スポンジに付けた縦線マーカー部分）の 上部と下部に同じ大きさで逆向きの力がかかっていることから， その二つの力が作る偶力（曲げモーメント） が，最終的な桁の抵抗力になって，車の重量を支えている。

という抵抗をすることになる。これは初学者にはとても難しい（第1著者も 学生のときにはさっぱりわからなかった）ことで， 今は理解できなくてもいい。章-2, 4で学んで欲しい。

図: 縦長と横長，どっちが強い

では同じ長方形断面の桁を，写真-のように 縦向きに置いたときと，横向きに置いたときとで， どちらが強いだろう。答は前者なのであるが， その裏には章-2, 4で習う 次式の断面2次モーメント と断面係数

$$I\equiv\dfrac{b h^3}{12}, \quad W\equiv\dfrac{b h^2}{6}$$

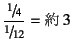が，抵抗係数として関与しているからである。 ただし，$b$が桁の断面の幅で$h$が高さである。 具体的には，変形のし難さを示す抵抗はこの$I$に比例し， 幅$b$には比例するだけだが， 桁の高さ$h$についてはその3乗($h^3$)に比例して強くなる。 抵抗力の度合の場合には，$W$，つまり$h$の2乗($h^2$)に比例して強くなる。 この模型断面の寸法$3.5\times 6$ (cm)を用いて$I$を計算すると， 縦長の場合が63.0cm$^4$，横長が21.4cm$^4$で，その比は`2.94'になる。 実測されたたわみは写真-の下の写真のように， 縦長の場合が約4mm，横長が約12mmとなるので， たわみ難さの比がおよそ $\dfrac{\slfrac{1}{4}}{\slfrac{1}{12}} = \mbox{約} 3$，つまりこれが上述の`2.94'に相当するのである。

図: 効率的な断面形状とその性能比較表および実例

このことから，図-に示した 同じ幅$b$を持つ三つの断面を， 一番左の矩形断面を基準にして比較するとその下の表のような比になる。 コストと抵抗力を比較して総合的に判断すれば， 一番右のI形断面が経済的・力学的に合理的であることがわかる。 こういったことを，この文書がカバーしている「構造力学」という科目で習い， それを身に付けていれば，より合理的な橋梁デザイン^1.4ができるようになる。

この図-の一番右の断面は， 厚い板（フランジ）を上下方向に縦の薄い板（ウェブ）で距離を離しているだけだ。 これは皆どこかで見たことのある形ではないだろうか。 そう，図-に示した線路のレールの断面と同じである。 この図のようにレール は，バラスト（砂利）でできた弾性的に抵抗する床の上に， 枕木を介して支えられた「けた」と同じ抵抗作用で， 列車を支えている。 だから，抵抗係数（曲げ剛性）を大きくする必要が あって，図の左に黒い図形で示したようなI形のような断面になっているのである。

ところで，毛利元就の 「3本の矢」という逸話がある。Wikipedia^1.5から引用すると

ある日、元就は三人の息子（隆元・元春・隆景）を枕元に呼び寄せ、1本の矢を 折るよう命じた。 息子たちが難なくこれを折ると、次は3本の矢束を折るよう命じたが、 息子たちは誰も折ることができなかった。 元就は一本では脆い矢も束になれば頑丈になるということを示し、 三兄弟の結束を強く訴えかけた＜後略・注略＞

というものだ。では逆に，三人で力を合わせたら折ることができただろうか。 半径$r$の1本の円形断面の断面2次モーメントと 断面係数は $I_0=\slfrac{\pi r^4}{4}$, $W_0=\slfrac{\pi r^3}{4}$である。 もし矢を横に並べ$\MouriA$のようにすると 断面2次モーメントも断面係数も3倍になるだけだから 三人で力を合わせたら折ることができただろう。 しかし，もし矢を$\MouriB$のように組むと， 断面2次モーメントは$11I_0$と1本の11倍になり，上下端の 断面係数が $W\subsc{u}=\slfrac{33 W_0}{\left(3+2\sqrt{3}\right)} \simeq 5.11 W_0$, $W\subsc{l}=\slfrac{33 W_0}{\left(3+\sqrt{3}\right)} \simeq 6.97 W_0$になる。 折ることを議論するのであれば断面係数を 検討すればいいから，3本を三角形にくみ上げると5倍以上強くなることがわかる。 もしこの元就の逸話を作った人が構造力学を知っていたら，三人で3本の 矢を折るように命じて，例えば「つまり凡庸な戦略なら3倍の軍勢が来たら負けるかも しれないが，いい軍師を雇用して戦略を練ることによっては5倍の軍勢に 対しても国を守ることができる。」とでも追加していたかもしれない。 呵呵。閑話休題。

図: プレートガーダと2主桁橋梁の標準的な断面

図: 桁高と曲げモーメントの大小

最初に示した桁橋の例の牛越橋も，実は，下からみるとI形断面の 桁2本（主桁）に支えられていることがわかる。写真-の 右に示したような断面の主桁が プレートガーダ（鈑桁ばんげた） と呼ばれ，この図は鋼の桁橋断面の代表例である。 「主桁」だけでなく「縦桁」や「横桁」も『I形断面』の 部材でできていることが多い。 ちなみに，写真からもわかるように，人や車だけではなく ライフライン（ガスや水道等）も渡していることに注意^1.6すべきである。

ではここで，桁の力学的な抵抗の特性を見るために， 主にフランジ部が材料の持つ最大の抵抗力$S$で 荷重を支えている状態を図-に示した。 簡単のために，薄いウェブはあまり抵抗しないものとして無視する。 上と下のフランジに，同じ大きさの最大抵抗力$S$が逆向きの力として発生し， それが作る偶力で荷重を支えているのだから， 図からも明らかなように，もし$h_1<h_2$であれば， 曲げモーメント（偶力）の「最大抵抗モーメント」も$M_1<M_2$となり， 右の断面の方が大きい抵抗力を持っていることになる。 これは「テコ」の原理から類推するとわかり易いだろう。

図: 孔開き板-- JR仙台駅新幹線14番ホーム

ここでは，ウェブと呼ばれる部分を 無視していたが，実際に橋を見に行くとわかるように， そこはかなりしっかりした板に見える。 本当に無視していいのだろうか。 実はウェブは，章-8で述べるような 意味で剛性を確保している部品であり，桁という構造の主要な働きを 考察する場合には，ある程度は無視してもいいのである。 例えば図-の 左の写真はJR仙台駅新幹線ホームであるが，天井を支えている梁を 見ると六角形の黒い部分が見える。 これはI形桁のウェブ板に六角形の孔が開いているのである。 いわゆる孔開き板 と呼ばれるもので，図-の右に 示したように，通常のI形桁を図のように切断し，AをA'に，BをB'に 合わせて，合わせた面をすべて溶接するとできあがる。 これで桁の高さも大きくできることになる。使われる箇所にもよるが， このくらいの孔は開いていてもいいということだ。

図: トラス構造--上弦材圧縮・下弦材引張り

1.2.0.0.2 トラス--桁からウェブを無くしてしまおう:

孔開き板を紹介したが，もしそれでもいいのなら， 上下フランジ間の距離をもっと離して，ついでにウェブの部分も ほどんど無くしてしまったらどうなるだろうか。 つまりそれは図-のようになる。 この形式をトラス と呼ぶ。

この形式の橋梁の場合には

• それぞれの部材（弦材）は桁ほどは太くなくてもいい。
• 桁高$h$を図のように大きくでき，つまり， 抵抗モーメントを大きくできる。
• 各弦材は，曲げではなく，単純に圧縮か引張りだけで抵抗すればいい。
• 弦材のつなぎ目（格点） は柔らかくてもいい。 極端には，格点は「ピン留め」でもいい。

という特徴をもつことになる。 弦材のつなぎ目がピンであったりして柔らかい（回転可能な）ので， 図のように，一つのパネルを三角形にして安定なものにし， それを連続して組み合わせて安定な構造にしている。

図: 引張り側はケーブル可

こうすることによって，上弦材は常に圧縮された状態で抵抗し， 下弦材は引張られた状態になる。 斜めの部材（斜材）は，その部材と荷重の位置関係によって 圧縮だったり引張りだったりするが， 桁のような曲げによる抵抗はほとんど生じないため， 個々の部材は単純な抵抗を持った構造になっている。 また下弦材は引張りだけの作用なので， 例えば福島市の松齢橋の上下の弦材を 注意深く観察すればわかるように，通常は下弦材は上弦材よりも 細くなっている。図-でもわざとそのように描いてみた。 極端なことを言えば，理屈上は下弦材はケーブルでもいいことになる。 模型でも写真-のように，糸にしても十分抵抗できている。 格点がピンでできている実例^1.7を写真-に示した。 この例の三角形のパネル以外に，鉛直材が入っているトラス等もあるが， それぞれの形式の特徴等については橋梁工学の本等を参考にして欲しい。 それぞれの形式にはそれぞれの力学的特徴があるのであろうが， 第1著者は不勉強なので，それについてはコメントできない。 個人的には，写真-の左奥に写っている新しい トラス橋のような正三角形を 並べただけのものより，福島市の松齢橋のような 曲弦トラスが増えて欲しいと感じているのではあるが。

図: トラス橋の例--伊達橋（福島の阿武隈川に架かる）
図: 元は鉄道橋，今は歩道橋
図: 格点はピン（大きなボルト）で接合

図: タイドアーチ

1.2.0.0.3 アーチ:

では，トラスの上弦材をもっとガッチリとした部材にして， 斜材をすべて取り除き， しかも下弦材を写真-のようにケーブルにしたものは どうだろう。写真-は， ちょっとだけ台形にした木片を7個並べて置いたもので， それぞれの木片同士は接着されていないが，下に「ひも」（タイ と呼ぶ）をつけてある。 木片の部分は，トラスの上弦材同様，主として 圧縮力で抵抗し，タイがトラスの下弦材と同じ引張りで抵抗している。 単に木片の重さ（と木片間の摩擦）だけで抵抗しているので，1個でも 取り去ると崩壊してしまう。 もちろん，タイを切った場合にも崩壊する。このように円弧のような形^1.8にした部材（アーチリブ と呼ぶ）で主に圧縮で抵抗する形式をアーチ と呼ぶ。

図: 普通のアーチの働き
図: 御霊屋橋（仙台の広瀬川）
図: アーチの働きの模型

図: コンクリートアーチと鋼アーチ
図: 大橋（広瀬川）--スパンドレルが埋まっている
図: 鋼アーチ橋の例-- 十綱とづな橋（福島飯坂温泉）

さて写真-は，これも 広瀬川に架かる御霊屋橋であるが，タイは見えない。 すなわち，写真-に示したように， もし地盤が強固で地盤反力が期待できるならば，タイは不要になる。 通常の多くのアーチにはタイは無く， 地盤が強固な場所にアーチが建設されていることを意味している。 実は，東京の隅田川に架かる「永代橋」がタイドアーチ であるが，「タイ」はケーブルではなく，桁の中に隠された鋼板になっている。 また，この御霊屋橋ではアーチの上に道路があるので「上路形式」に分類される。 この上路とアーチリブの間の部分をスパンドレル と呼ぶが， この御霊屋橋の場合はそこに鉛直材が配置されている。これに対して， 東北大学川内キャンパスに近い 「広瀬川に架かる大橋（写真-）」のように， スパンドレルが 埋まって（多分中空）いる場合もある。写真-は 鋼アーチの一例である。鋼アーチの場合のリブには，桁と同様，I形や箱形断面が よく用いられるが，この例の場合には，2対の溝形鋼を向き合わせて 造った（多分；呵呵）箱断面の比較的細い部材を造り，それを2本に して主なリブとして上下に配置し，その間を 筋交いで組んで1本のリブ（ブレーストリブ） にしていると思われる。

最新版を正確に読むためには pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。