 |
最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
最終的に,橋梁を「デザインする」という行為の ステップを大まかにまとめると,次のようになる。
![\begin{displaymath}
\begin{array}{llll}
\mbox{{\bf つり合い式:}} & \D*[2]{M}{x}+...
...{ult} =
\displaystyle\frac{M\sub{ult}}{W\sub{ult}}
\end{array}\end{displaymath}](s1img82.gif)
最終的には,モデルや解法に近似があるので, コンピュータの結果を正しく理解するために, 正しい力学の正確な知識と,章-5の 数値解析法の基礎知識とが必要になる。
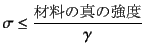 あるいは
あるいは
![]()
ただし,![]() は安全率
と呼ばれ,予想できない事態を想定した
安全のための余裕係数1.9(
は安全率
と呼ばれ,予想できない事態を想定した
安全のための余裕係数1.9(
![]() )である。
この「あるいは」を挟む二つのフローのうちの左側のフローは
許容応力(度)設計法
と呼ばれる設計法の考え方で,
右のは限界状態設計法
の中の終局状態設計法
の考え方に相当するが,本質的な安全確保の思想は同じである。
「あるいは」の右のステップにある
)である。
この「あるいは」を挟む二つのフローのうちの左側のフローは
許容応力(度)設計法
と呼ばれる設計法の考え方で,
右のは限界状態設計法
の中の終局状態設計法
の考え方に相当するが,本質的な安全確保の思想は同じである。
「あるいは」の右のステップにある![]() や
や![]() ,
, ![]() は,
上述の安全率
は,
上述の安全率![]() に相当する荷重係数
やその他の要因の余裕係数1.10である。
に相当する荷重係数
やその他の要因の余裕係数1.10である。
これが設計という行為の大まかなフロー1.12である。
現実に建設されているデータからまとめられた,
経済的・力学的に合理的な,形式とスパンの
組み合わせを表-![]() [123]1.13に示した。
例えば100 mの支間長の橋梁を設計しなければならないとしよう。
この表からわかることは,少なくとも8種類ほどの形式が可能であるということだ。
つまり,いわゆるデザイン(形式選定)の自由度はスパン毎にたくさんあり,
材料の選択(適材適所)も念頭に置くと,
設計の自由度は無限であることを示している。
もし読者が橋梁技術者として仕事をするのであれば,
架設現場付近の社会や文化を理解した上で,
それを活かして自由にデザインできる1.14ことを覚えておいて欲しい。
そして,そのデザインを実現するためには,
正しい力学の理解が必要であることもわかると思う。
[123]1.13に示した。
例えば100 mの支間長の橋梁を設計しなければならないとしよう。
この表からわかることは,少なくとも8種類ほどの形式が可能であるということだ。
つまり,いわゆるデザイン(形式選定)の自由度はスパン毎にたくさんあり,
材料の選択(適材適所)も念頭に置くと,
設計の自由度は無限であることを示している。
もし読者が橋梁技術者として仕事をするのであれば,
架設現場付近の社会や文化を理解した上で,
それを活かして自由にデザインできる1.14ことを覚えておいて欲しい。
そして,そのデザインを実現するためには,
正しい力学の理解が必要であることもわかると思う。
さて昨今は,パーソナルコンピュータ上で非線形の動的解析までできる 汎用プログラムが,以前よりは廉価で入手できる。それがあれば, どんな構造でも強度計算はできてしまう。だから構造力学の勉強は しなくてもいい!・・・と言えるだろうか。数値解析は,数値を入力しなければ できない。どんな断面の形がいいのか教えてはくれない。ケーススタディは できても,普遍的な特性を教えてくれることはない。例えば,この章の 最初の方で述べたような,縦長の断面と横長の断面のどちらがどのくらい 強度が大きくて,そしてそれはなぜなのかについて 数値解析法は教えてはくれない。のちに学ぶ座屈における細長比と構造の 境界条件等との関係や,動的解析における固有振動数とモードと構造形態や 境界条件との関係については,やはり力学として学んで身に付けておかなければ, 数値解析ツールを使う資格は無いと思う。文献[86]で 引用されていたのだが,茶道の心得1.15に 「守・破・離」というものがあるらしい。「守」とは,ひたすら学ぶ (覚える)こと。「破」は,教えの言葉から抜け出して真意を会得すること。 「離」とは,型にはとらわれないで自由に飛翔する境地で,順に, 下手・上手・名人と対比されるらしい。多分「守」がなければ その上も無いということではないのだろうか。キュビズムの流れの中の ある独自のものを発展させたピカソのデッサン力や 対象を写しとる技術がものすごいということは, 読者も知っていると思う。やはり,常に必要なのは基本1.16である。 力学は,社会基盤構造に携わる技術者の基本・心得1.17であると考えている。
さて,「工学」は「理学1.18」と同じく「自然科学」 で1.19ある。 『「科学」は 「予測すること」と同義』1.20であり,そのためには, 何らかの科学的な道具, すなわち構造物を設計する場合には「物理」や「数学」「化学」を用いて, 建設したあとの性能(performance)を予測しなければならない。 これが「デザイン」という行為である。 狭い意味での「デザイン(意匠)」の場合であっても同様に, 建設後の表現を,心理学や社会学等の「社会科学」的道具を用いて 「科学した」上で決定している1.21のと 同じである。 「理学」が事実の裏に秘めた真実を予測・探求するのに対し, 「工学」は真実を追いながらも,それがほぼ不可能なくらいの複雑な系を 対象としているために,事実(実現象)を説明できる真実のかけらや モデルを構築し,さらに適切な予測ツールを開発して, それを用いることによって社会にできるだけすぐに役立たせようとする学問である。