最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
写真-![]() に示したように,
部材の接合点がピンあるいは柔らかい板で結合された,
三角形を基本構造とする部材組み構造をトラス
と呼ぶ。トラスは古くから鉄道橋2.5でも多く用いられ,
既に100年以上経った橋梁もあるが,
体育館・ドーム等の天井や鉄塔にもトラス構造が使われている。
トラス部材は,図-2.5のバネモデルのように,
その部材方向の伸び縮みという変形で抵抗する,最も単純な抵抗則を持っている。
したがって,内力も図-2.6のモデルのように,
その部材軸方向の力だけになる。
に示したように,
部材の接合点がピンあるいは柔らかい板で結合された,
三角形を基本構造とする部材組み構造をトラス
と呼ぶ。トラスは古くから鉄道橋2.5でも多く用いられ,
既に100年以上経った橋梁もあるが,
体育館・ドーム等の天井や鉄塔にもトラス構造が使われている。
トラス部材は,図-2.5のバネモデルのように,
その部材方向の伸び縮みという変形で抵抗する,最も単純な抵抗則を持っている。
したがって,内力も図-2.6のモデルのように,
その部材軸方向の力だけになる。
なぜ三角形を基本としているかについては,
右の写真-2.7から一目瞭然であろう。
接合点をピンと考えていいため,割り箸を糸で緩く組み立てて作った
模型にしてみた。
当然なことに,四角形では不安定で自立すらできないが,三角形であれば安定する。
しかも写真-![]() に示したように,荷重がこのように
作用している場合の下の部材は糸(ケーブル)でも安定している。
これは上述のように,
各部材が単に圧縮か引張りのみを受けている場合が多いためであり,
力学的には非常に単純でわかり易い構造になっているからである。
そのため,引張り部材をケーブルで代用しても,
構造全体は安定で強度も確保できることになる。
に示したように,荷重がこのように
作用している場合の下の部材は糸(ケーブル)でも安定している。
これは上述のように,
各部材が単に圧縮か引張りのみを受けている場合が多いためであり,
力学的には非常に単純でわかり易い構造になっているからである。
そのため,引張り部材をケーブルで代用しても,
構造全体は安定で強度も確保できることになる。
トラスもそれ以外の社会基盤構造と同様,実際には3次元的な広がりを持つ。
したがって,厳密には図-2.8のような
奥行き方向も考慮した立体トラスとして考えなければならない。
しかしながら,まず主構造としての平面トラスで設計した上で,
奥行き方向を別途設計することが普通であり,
また,この文書では最も単純な構造の例としてトラスを取り上げることから,
ここでは図-2.9に示したような平面トラスのみを
取り扱う。
なお実際の部材には太さがあるが,以下たいていの場合はこの図のように,
部材を1本の太い線で表すので注意すること。またトラスの場合は部材の
結合点はピンのようなものであるが,![]() 印は原則略す。
印は原則略す。
トラスには,重要な特徴が二つある。
特徴1で定義した節点については,写真-![]() の
右の写真から実際の状況2.6は理解できると思う。
ピンの働きは,
コンパスの足の結合点や自転車のペダルの取り付け部を思い描けば
想像できるだろう。
したがって,部材は節点を中心として曲がることなく(まっすぐなまま)回
転することができる。
また,二つの特徴から導かれる結論は,
トラス部材1本の抵抗力つまり内力は軸力だけだということである。
の
右の写真から実際の状況2.6は理解できると思う。
ピンの働きは,
コンパスの足の結合点や自転車のペダルの取り付け部を思い描けば
想像できるだろう。
したがって,部材は節点を中心として曲がることなく(まっすぐなまま)回
転することができる。
また,二つの特徴から導かれる結論は,
トラス部材1本の抵抗力つまり内力は軸力だけだということである。
特徴2については疑問を感じると思う。つまり,実際にトラス橋の上を車や 列車が通過することを想像すると,直接部材の上を通っているように見え, したがって節点にだけでなく,部材にも直接荷重が作用するように 感じられるかもしれない。 しかし実際には,図-2.10に誇張して示したように, 横桁・縦桁を介して主トラス構造の節点のみに荷重が作用するようになっている。
トラスの内力を,断面に生じている抵抗力であることから断面力, あるいは部材の軸方向の力なので軸力 と呼ぶことにする。 前節でも述べたように,断面力は部材を仮想的に(頭の中で)切断しないと 見ることができないが,この断面を仮想的に切断する方法には
の2種類がある。前者を「節点法」,後者を「断面法」と呼ぶ。 ただし,部材を切断する場合には
という約束がある。
節点法の手順をまとめると以下の通りになる。
図-2.11に示した正三角形のトラス構造を例にとって説明しよう。
力およびモーメントのつり合い条件から支点反力を
求める[手順1]と,
![]() ,
,
![]() になる。
各節点で部材を切断し,
未知数としての軸力を作用させる[手順2(図-2.12)]。
切断の約束1に従い,各節点に逆向きで同じ大きさの力を
作用させる[手順3(図-2.13)]。
まず点Aでのつり合いは
になる。
各節点で部材を切断し,
未知数としての軸力を作用させる[手順2(図-2.12)]。
切断の約束1に従い,各節点に逆向きで同じ大きさの力を
作用させる[手順3(図-2.13)]。
まず点Aでのつり合いは
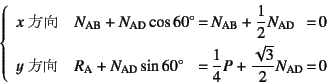
となるので,
![]() ,
,
![]() と
各断面力が求められる。
と
各断面力が求められる。
次は点Bではなく,端点である点Cでのつり合いを考えてみよう。それは
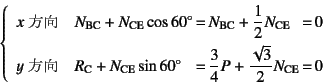
となるので,
![]() ,
,
![]() のように
軸力が求められる。次に点Dでのつり合いは
のように
軸力が求められる。次に点Dでのつり合いは
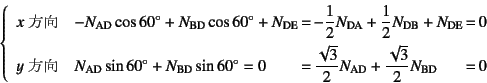
となるから,
![]() ,
,
![]() が各軸力の値である。
最後に点Eでの
が各軸力の値である。
最後に点Eでの![]() 方向のつり合いから
方向のつり合いから
となり,
![]() が求められる。
これですべての軸力が求められたので,
点Bにおけるつり合いは考える必要が無くなったが,
練習のために各自確かめて欲しい。
が求められる。
これですべての軸力が求められたので,
点Bにおけるつり合いは考える必要が無くなったが,
練習のために各自確かめて欲しい。
断面法の手順は以下の通りである。
この方法を用いて,再度図-2.11のトラスの三つの軸
力
![]() ,
,
![]() ,
,
![]() を求めてみよう。
を求めてみよう。
まず全体のつり合いから
支点反力を求める[手順1]と,
![]() ,
,
![]() となる。
この場合の切断方法は,図-2.14のように[手順2]した。
切断されたトラスの左側に対してつり合いを考える[手順3]と,
となる。
この場合の切断方法は,図-2.14のように[手順2]した。
切断されたトラスの左側に対してつり合いを考える[手順3]と,![]() 方向の
つり合いより
方向の
つり合いより
となり,![]() 方向のつり合いより
方向のつり合いより
となる。
したがって
![]() と求められる。
モーメントのつり合いはどこを中心に考えてもいいが,式中の未知数は
少ない方が楽であり間違いも少ないだろうから,B点を中心に考えてみよう。
すると
と求められる。
モーメントのつり合いはどこを中心に考えてもいいが,式中の未知数は
少ない方が楽であり間違いも少ないだろうから,B点を中心に考えてみよう。
すると
となるので,
![]() が求められる。
以上から,
が求められる。
以上から,
![]() と
と
![]() を
上式(
を
上式(![]() )に代入すると,
最終的に
)に代入すると,
最終的に
![]() と求められ,
節点法の答と一致する。
各自の練習のために,他の軸力も同様にして求めて欲しい。
得られた軸力分布を図-2.16に示した。
と求められ,
節点法の答と一致する。
各自の練習のために,他の軸力も同様にして求めて欲しい。
得られた軸力分布を図-2.16に示した。
断面法を用いて計算を行う場合には,特に切断箇所には注意しなければならない。 例えば図-2.17は間違った切断方法の例である。 まず図-2.17(a)では四つの部材を切断しているため, 未知数である軸力は四つになっているにもかかわらず, つり合い式は三つしか立てられないため条件が一つ不足し, 軸力を唯一に求めることはできない。 次に図-2.17(b)では三つの部材を切断してはいるものの, トラスが二つに分断されていないために,切断の約束2を 適用することができない。 そのため,トラス全体に対するつり合い式しか立てることができず, 各軸力は逆向きに同じ大きさで作用しているために打ち消しあうだけで, 結果として得ることができるのは支点反力だけである。
前節の例では,まず荷重の大きさとそれが作用する点が与えられた上で 軸力を求めていた。 機械部品のような場合はそれでよさそうだ。 しかし,実際の橋梁を設計する場合はどうだろう。 普段橋梁に作用している主な荷重は自重(死荷重)と自動車等の 荷重(活荷重)である。 自重は常に同じ強度で常に同じ場所に作用していると考えていいが, 自動車等の荷重は大型車と小型車で重量が異なる上に, 橋の幅方向・長さ方向共にどの部分にどのように載るかについては 決まっているわけではなく,またそれは時々刻々変化する。 したがって,あるトラス部材を設計するためには,その部材に生じるであろう 軸力が最大になるような荷重の位置を決めた上で, その最大軸力を求める必要がある。そのためには, その部材が最も危なくなる(軸力が最大になる)ように 自動車等を並べる必要があるのである。 つまり設計する部材毎に荷重の載せ方は異なるのである。
現行の設計法では,橋梁の主部材を設計する場合の自動車等の
荷重は,図-2.19に示したような,
ある種の渋滞交通荷重(L荷重
)でモデル化[128]されている。
これは,ある幅![]() の部分には
の部分には![]() の強度で,
それ以外の箇所には
の強度で,
それ以外の箇所には![]() の強度で,ある指定された
分布外力が載ることを意味する。
の強度で,ある指定された
分布外力が載ることを意味する。![]() ,
, ![]() の値の求め方に
ついては節-A.2を参照のこと。
そこでまず,この分布荷重をどこに載せたときに設計しようとしている部材が
最も危険になるのか調べる必要がある。
の値の求め方に
ついては節-A.2を参照のこと。
そこでまず,この分布荷重をどこに載せたときに設計しようとしている部材が
最も危険になるのか調べる必要がある。
そのためには,単位の大きさを持った集中荷重(注意:単位は無い)を 床版に載せ, その場所を移動させることによって, 設計しようとしている断面がどの程度の軸力で抵抗するのか, 予め探査しておく必要がある。 ちょうど,患者の顔色や反応を見ながら医者が触診によって病気の原因を探すのと 同じように,どの位置の荷重が設計断面にとって どのくらい「辛い」のかについて探るのである。 このような「辛さ」の関数を影響線 と呼んでいる。
図-2.20に示したような,正三角形のパネルで
できたトラスの部材U, D, Lの影響線を求めてみよう。
下路だとして,まず節点![]() , 2, 3の位置に大きさ1の集中荷重が作用したときの
軸力を求める。
, 2, 3の位置に大きさ1の集中荷重が作用したときの
軸力を求める。![]() の位置に荷重があるときの図を左から二番目に描いた。
図のように内力を記すと,力のつり合いとモーメントのつり合いは
の位置に荷重があるときの図を左から二番目に描いた。
図のように内力を記すと,力のつり合いとモーメントのつり合いは
である。支点反力は
![]() であるから,各軸力は
であるから,各軸力は
と求められる。
同じように節点![]() , 3に荷重があるときのつり合いは,右端の図から
, 3に荷重があるときのつり合いは,右端の図から
となるので,各軸力は
となる。支点反力は
![]() ,
,
![]() である。
である。
次に荷重が節点と節点の間にあるときを考えてみよう。
先に図-2.10に示したように,
床版上の荷重は縦桁・横桁を通して節点に伝達される。
したがって,節点間に集中荷重があるときには,
その荷重は両方の節点に図-2.21のように
分配されると考えなければならない。
したがって,節点![]() から
から![]() 離れた点に荷重があるときの影響線は,
節点に荷重が作用したときの上で求めた値
離れた点に荷重があるときの影響線は,
節点に荷重が作用したときの上で求めた値
![]() ,
,
![]() ,
D, L (
,
D, L (![]() , 1, 2, 3)を用いて
, 1, 2, 3)を用いて
になることは容易に理解できるだろう。
つまり,載荷位置![]() の関数として捉えた影響線は,
節点に作用したときの影響線の値を線形補間すれば(直線で結べば)いいことになる。
このようにして描いたのが図-2.22である。横軸の
の関数として捉えた影響線は,
節点に作用したときの影響線の値を線形補間すれば(直線で結べば)いいことになる。
このようにして描いたのが図-2.22である。横軸の![]() は単位荷重の載荷点であることに十分注意しなければならない。
は単位荷重の載荷点であることに十分注意しなければならない。
上弦材Uの影響線は常に負の値であることから,荷重がどこに載っても
常に圧縮力が生じていることがわかる。逆に下弦材Lは常に引張りで抵抗する。
これに対し,斜材Dの影響線は
![]() までは正の値をとることから,
その範囲に荷重が載ると引張り抵抗をすることになる。
そして
までは正の値をとることから,
その範囲に荷重が載ると引張り抵抗をすることになる。
そして
![]() の部分に荷重がある場合には圧縮力が生じている。
実は,今はわからなくてもいいが,引張りと圧縮で強度が異なる場合がある。
したがって斜材は通常,圧縮および引張りの両方に抵抗できるように
設計されなければならないことがわかる。
の部分に荷重がある場合には圧縮力が生じている。
実は,今はわからなくてもいいが,引張りと圧縮で強度が異なる場合がある。
したがって斜材は通常,圧縮および引張りの両方に抵抗できるように
設計されなければならないことがわかる。
このようにして求めた影響線を用いれば,設計する部材にとって
最も不利になるように(辛くなるように)設計荷重を載せる場所を決定できるのだが,
まず例として,ある荷重の大きさと載荷位置が与えられたとして,
影響線を用いて軸力を求める方法を考えてみよう。
例えば図-2.23の一番左の図を見て欲しい。
影響線は大きさ1の集中荷重(単位は無い)が載ったときの軸力だったから,
もし左から![]() の位置に集中荷重
の位置に集中荷重![]() (単位は例えばN)が作用したときの
下弦材の軸力は
(単位は例えばN)が作用したときの
下弦材の軸力は![]() (単位はN)になることは容易に理解できると思う。
では,中の図のように
(単位はN)になることは容易に理解できると思う。
では,中の図のように![]() の位置に
の位置に![]() が載った場合には
当然
が載った場合には
当然![]() が軸力になる。したがって,もし両方の荷重が
同時に作用している場合に下弦材に生じる軸力は,
この二つを重ね合わせて
が軸力になる。したがって,もし両方の荷重が
同時に作用している場合に下弦材に生じる軸力は,
この二つを重ね合わせて
![]() になるのもわかると思う。
になるのもわかると思う。
では,一番右の図のように強度![]() (単位はN/m)の
一様な分布荷重が作用した場合にはどうすればいいだろう。
そこで分布荷重をあたかも集中荷重の集合のように捉えるために,
その分布荷重のある位置
(単位はN/m)の
一様な分布荷重が作用した場合にはどうすればいいだろう。
そこで分布荷重をあたかも集中荷重の集合のように捉えるために,
その分布荷重のある位置![]() の微小区間
の微小区間![]() 分の荷重
分の荷重
![]() が
点
が
点![]() に作用している「集中荷重」だと解釈してみよう。
そうすると下弦材の軸力は
に作用している「集中荷重」だと解釈してみよう。
そうすると下弦材の軸力は
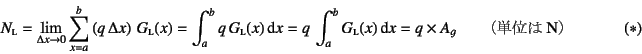
になるのも理解できるだろう。分布荷重が一様なので積分の外に出すことができ,
したがって最後の等式が示すように,
影響線面積![]() (単位はm)に
(単位はm)に![]() を乗じれば下弦材の軸力が算定できる。
を乗じれば下弦材の軸力が算定できる。![]() は
図の網掛けした部分の面積である。
このように,一旦影響線を求めておけば,任意の荷重に対する軸力を
容易に求めることができる。
この性質を逆に使って,荷重の位置を決めようというのである。
は
図の網掛けした部分の面積である。
このように,一旦影響線を求めておけば,任意の荷重に対する軸力を
容易に求めることができる。
この性質を逆に使って,荷重の位置を決めようというのである。
さて図-2.19に示したように,
橋梁の主部材を設計する場合には二段階の大きさの
等分布荷重を作用させることになっている。
そこで,この分布荷重をどのように載せると,設計しようとしている部材が
最も危険に(辛く)なるのか決めるために,影響線を用いることを説明しよう。
ここでは簡単のために,![]() mとし,トラスの1パネルの長さも
mとし,トラスの1パネルの長さも![]() mと
して,影響線が単純な分布をしている上弦材を例にして,その設計をしてみよう。
単位を揃えるために
mと
して,影響線が単純な分布をしている上弦材を例にして,その設計をしてみよう。
単位を揃えるために![]() ,
, ![]() もN/mの単位で与えられているものとする。
上式(
もN/mの単位で与えられているものとする。
上式(![]() )のように,分布荷重が作用したときの軸力は,
分布荷重の強度と影響線面積を乗じればよかった。
したがって,影響線の面積ができるだけ大きい箇所に,
強い強度の
)のように,分布荷重が作用したときの軸力は,
分布荷重の強度と影響線面積を乗じればよかった。
したがって,影響線の面積ができるだけ大きい箇所に,
強い強度の![]() を分布させればいいことがわかる。
そこで図-2.24に示したように,左端から
を分布させればいいことがわかる。
そこで図-2.24に示したように,左端から![]() の
位置から
の
位置から![]() を載せ,図の網掛け部分の面積が最大になるように
を載せ,図の網掛け部分の面積が最大になるように![]() を
決定しよう。
を
決定しよう。
この網掛け部分の面積(負)は,例えば
となるので,
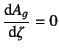 を計算すると
を計算すると
が求められる。すなわち,左端から7.5mの位置から![]() を10m分だけ
載せたときに,上弦材には最大の軸力が発生することを意味する。
この
を10m分だけ
載せたときに,上弦材には最大の軸力が発生することを意味する。
この
![]() を上式に代入して
面積を求めると
を上式に代入して
面積を求めると
![]() になる。
また,左の白い三角形の面積は
になる。
また,左の白い三角形の面積は
![]() ,右の
白い三角形の面積は
,右の
白い三角形の面積は
![]() であるから,
合計
であるから,
合計
![]() になる。
したがって,図-2.19の設計用の荷重が載ったときに,
上弦材に発生する最大軸力
は
になる。
したがって,図-2.19の設計用の荷重が載ったときに,
上弦材に発生する最大軸力
は
と求められる。
あるいは図-2.24の影響線の全面積を![]() と
すると,
と
すると,
![]() となり,これを用いて
となり,これを用いて
![]() でも
同じだ。
この算定の仕方の方が,上の
でも
同じだ。
この算定の仕方の方が,上の
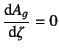 にする意味は
わかり易いかもしれない。いずれにしても,
これに対して部材が破壊しないように断面を設計すればいいことになる。
にする意味は
わかり易いかもしれない。いずれにしても,
これに対して部材が破壊しないように断面を設計すればいいことになる。
トラス部材は単純に軸力を発生して抵抗する物体である。
そこで簡単のために,トラス部材を図-2.25のような
バネで置き換え,左上の1本のバネは力![]() までは壊れずに支えられるとしよう。
そのバネを下の図のように2本直列にしても,支えられる力は
までは壊れずに支えられるとしよう。
そのバネを下の図のように2本直列にしても,支えられる力は![]() のままで
あることはすぐにわかるだろう。しかし,右上のように並列にすると,
それぞれが
のままで
あることはすぐにわかるだろう。しかし,右上のように並列にすると,
それぞれが![]() まで支えるので,合計で
まで支えるので,合計で![]() までの力を支えることができる。
したがってトラス部材の場合にも,同じ材料で造るなら,
太くすればするほど強い構造になることは容易に推測できるだろう。
つまり,部材の断面積を大きくすれば強くなるのである。
このことから,材料規格では単位面積当たりの
抵抗圧力(応力おうりょく
と呼ぶ)の最大値でその強度が規定されている。
までの力を支えることができる。
したがってトラス部材の場合にも,同じ材料で造るなら,
太くすればするほど強い構造になることは容易に推測できるだろう。
つまり,部材の断面積を大きくすれば強くなるのである。
このことから,材料規格では単位面積当たりの
抵抗圧力(応力おうりょく
と呼ぶ)の最大値でその強度が規定されている。
例えば前節の上弦材に使いたい材料の圧縮強度
![]() が,単位面積当たりの圧力値(応力値)として決められている場合,
断面積
が,単位面積当たりの圧力値(応力値)として決められている場合,
断面積![]() の上弦材が支えることができる
最大の断面強度は
の上弦材が支えることができる
最大の断面強度は
![]() になる。
これが,前節で求められた最大軸力
になる。
これが,前節で求められた最大軸力
![]() より
大きければ,その部材は安全に設計されたことになる。つまり,前節の
上弦材が安全を確保できるためには,
(断面の強度)
より
大きければ,その部材は安全に設計されたことになる。つまり,前節の
上弦材が安全を確保できるためには,
(断面の強度)![]() (実際に生じる軸力)であればいいのだから
(実際に生じる軸力)であればいいのだから
| (2.6) |
になるように断面積![]() を決定すれば(断面を設計すれば),
安全な設計ができたことになる。
を決定すれば(断面を設計すれば),
安全な設計ができたことになる。
下弦材の場合には節点![]() で影響線が最大値をとることから,
やはりその前後に
で影響線が最大値をとることから,
やはりその前後に![]() の強度の荷重を載せるようにして,
影響線面積が最大になるようにその位置を決定すればいい。
結局図-2.26のように載荷する位置を探し出し,
影響線面積を用いて
の強度の荷重を載せるようにして,
影響線面積が最大になるようにその位置を決定すればいい。
結局図-2.26のように載荷する位置を探し出し,
影響線面積を用いて
![]() を算定しさえすれば,
上弦材と同様
を算定しさえすれば,
上弦材と同様
| (2.7) |
を満足するように,断面を設計すればいいことになる。
ここで
![]() は引張りに対する材料強度
である。
一方斜材の場合には,載せる場所によって軸力の符号が変化するため,
圧縮と引張りに対して別々に最大軸力を求める必要がある。
具体的には図-2.27のようになり,
この上の図に示したような載荷状態に対して引張りの
最大軸力
は引張りに対する材料強度
である。
一方斜材の場合には,載せる場所によって軸力の符号が変化するため,
圧縮と引張りに対して別々に最大軸力を求める必要がある。
具体的には図-2.27のようになり,
この上の図に示したような載荷状態に対して引張りの
最大軸力
![]() を算定し,
下の図のような載荷に対して圧縮の最大軸力
を算定し,
下の図のような載荷に対して圧縮の最大軸力
![]() を
計算しなければならない。そのようにして最大軸力を得たあと,
上弦材と同様にして
を
計算しなければならない。そのようにして最大軸力を得たあと,
上弦材と同様にして
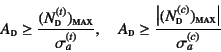 |
(2.8) |
のいずれもが満足されるように,
断面積![]() を決定(設計)することになる。
材料強度が圧縮と引張りで異なるのは奇妙に感じられるかもしれない。
しかし,使う材料によってはそのようなことがある。例えばコンクリートは
圧縮には強いが,引張られるとすぐにひびが入って壊れることがある。
あるいは章-6で説明する座屈現象のために,
圧縮と引張りとでは強度が
異なる(節-6.4.5, 6.4.6の
式(6.56) (6.57)参照)ことが
あるので,このような2重の確認が必要になる2.7のである。
を決定(設計)することになる。
材料強度が圧縮と引張りで異なるのは奇妙に感じられるかもしれない。
しかし,使う材料によってはそのようなことがある。例えばコンクリートは
圧縮には強いが,引張られるとすぐにひびが入って壊れることがある。
あるいは章-6で説明する座屈現象のために,
圧縮と引張りとでは強度が
異なる(節-6.4.5, 6.4.6の
式(6.56) (6.57)参照)ことが
あるので,このような2重の確認が必要になる2.7のである。