最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
トラス構造の安定性には2種類ある。
一つは全体的な支持条件に関するもので,反力の数によって決まるものであるが,
これは構造全体が動かないように支えられているかどうかに関わるものである。
もちろん社会基盤構造としては動き続けるような構造物は役に立たないが,
飛行中の航空機も構造物の一つではある。さて,
支点反力の数を![]() とするとき
とするとき
| (2.19) |
によって定義される
![]() を外的不静定次数
と呼び,
を外的不静定次数
と呼び,
![]() の
場合が「外的不安定」,
の
場合が「外的不安定」,
![]() のときが
「外的静定」,
のときが
「外的静定」,
![]() のときが「外的不静定」と
呼ばれる。
「(不)静定」の意味は今はわからなくていい。
のときが「外的不静定」と
呼ばれる。
「(不)静定」の意味は今はわからなくていい。
例えば,前節で扱った図-2.4のトラスで検討しよう。
この場合には反力は三つだったので,
![]() となり
外的静定である。
ここでもし,右側の支点も左右には移動できないようにできたとしよう。
するとAとBを結ぶ長さ
となり
外的静定である。
ここでもし,右側の支点も左右には移動できないようにできたとしよう。
するとAとBを結ぶ長さ![]() の水平な部材は
両端を地盤に固定されてしまっているので,
存在そのものに意味が無くなるが,
反力は四つになるから
の水平な部材は
両端を地盤に固定されてしまっているので,
存在そのものに意味が無くなるが,
反力は四つになるから
![]() となり,
これを外的不静定と呼んでいる。
この場合は,建設が終了した時点で温度が上昇した場合,
この水平な部材ABは温度に伴って自由に伸びることを抑制されてしまい,
外力も作用していない状態で圧縮力が生じてしまう。
これも一般には不都合であろう。
しかも,四つの未知の反力に対し,外力と反力の力のつり合いとモーメントの
つり合いとで三つの条件式しかないことから,その反力を求めることができない。
さてどうしたらいいだろう。
となり,
これを外的不静定と呼んでいる。
この場合は,建設が終了した時点で温度が上昇した場合,
この水平な部材ABは温度に伴って自由に伸びることを抑制されてしまい,
外力も作用していない状態で圧縮力が生じてしまう。
これも一般には不都合であろう。
しかも,四つの未知の反力に対し,外力と反力の力のつり合いとモーメントの
つり合いとで三つの条件式しかないことから,その反力を求めることができない。
さてどうしたらいいだろう。
逆に図-2.4のトラスで,
もし左側の支点も左右に移動できるものとすると,
反力は二箇所の支点での上向きの![]() ,
, ![]() の二つだけに
なるので,
の二つだけに
なるので,
![]() となり,外的不安定である。
つまり,この三角トラスは左右方向には一切固定されていないため
安定ではなく(静止してはいられなくなり),運動方程式
となり,外的不安定である。
つまり,この三角トラスは左右方向には一切固定されていないため
安定ではなく(静止してはいられなくなり),運動方程式
を満たす運動をすることが可能になる。
ここに![]() はトラスの全質量,
はトラスの全質量,![]() はトラス全体の
はトラス全体の![]() 方向の移動量である。
したがって,
何らかの外乱があれば(風が吹けば)
方向の移動量である。
したがって,
何らかの外乱があれば(風が吹けば)![]() 方向に等加速度運動をすることになる。
これは,この章の初めで「つり合い」の定義を示したときにも述べた。
構造自体は外力を支えられるものの,自由に移動できるため,
外的に不安定になっていると呼んでいる。
方向に等加速度運動をすることになる。
これは,この章の初めで「つり合い」の定義を示したときにも述べた。
構造自体は外力を支えられるものの,自由に移動できるため,
外的に不安定になっていると呼んでいる。
もう一つは内的安定性と呼ばれるもので,
構造自体の安定性に関わったものである。
これは写真-2.7の四角形のトラスが
自立しないことに関係している。
部材の総数を![]() ,節点の総数を
,節点の総数を![]() とするとき
とするとき
| (2.20) |
で定義される
![]() を内的不静定次数
と呼ぶ。
を内的不静定次数
と呼ぶ。
![]() の場合には
「内的不安定」,
の場合には
「内的不安定」,
![]() の場合には
「内的静定」,
の場合には
「内的静定」,
![]() の場合には「内的不静定」である
と呼ばれる。
の場合には「内的不静定」である
と呼ばれる。
例として,図-2.56(a)の
左図に示すような四角形の構造を眺めてみよう。
この構造に横方向から荷重を作用させると右図のように潰れてしまうことから,
不安定であるのは明らかであるが,
この構造は![]() ,
, ![]() なので
なので
![]() となる。
つまり,支持は適切になされていても,構造自体が不安定なものを
内的不安定な構造と呼んでいる。
一方,図-2.56(b)のように部材を一つ増やし,
二つの三角形からなる構造の場合には,
となる。
つまり,支持は適切になされていても,構造自体が不安定なものを
内的不安定な構造と呼んでいる。
一方,図-2.56(b)のように部材を一つ増やし,
二つの三角形からなる構造の場合には,![]() なので
なので
![]() となる。したがって,荷重を作用させても潰れることなく三角形の形状は保たれる。
これを「内的静定」と呼んでいる。さらに図-2.56(c)のように
もう1本部材を増やした場合には
となる。したがって,荷重を作用させても潰れることなく三角形の形状は保たれる。
これを「内的静定」と呼んでいる。さらに図-2.56(c)のように
もう1本部材を増やした場合には![]() となる
ことから
となる
ことから
![]() になり,
内的不静定と呼ばれる構造になる。
ただし,内的不静定な構造は安定で,内的静定な構造よりもある意味で
余裕がある(冗長である)。つまり,図-2.56(c)の
構造から部材を一つ取り外した(壊れた)としても,
それは内的静定になるだけで全体構造は壊れない。
実は最後の例の内的不静定な構造が持つ冗長性
には,耐震構造等を考える場合には重要な意味がある。
つまり,予測できなかったような何らかの原因で1本の部材が破壊したとしても,
構造全体はまだ安定のままでいられるからである。
になり,
内的不静定と呼ばれる構造になる。
ただし,内的不静定な構造は安定で,内的静定な構造よりもある意味で
余裕がある(冗長である)。つまり,図-2.56(c)の
構造から部材を一つ取り外した(壊れた)としても,
それは内的静定になるだけで全体構造は壊れない。
実は最後の例の内的不静定な構造が持つ冗長性
には,耐震構造等を考える場合には重要な意味がある。
つまり,予測できなかったような何らかの原因で1本の部材が破壊したとしても,
構造全体はまだ安定のままでいられるからである。
この章の最後で説明するが,「内的安定性」を「外的安定性」と同様に
力との関係で捉えるならば,内力を力のつり合いのみで求められる場合を
「(内的)静定」,そうでない場合を「(内的)不静定」と
呼んでいることになる。
外的不静定次数と内的不静定次数との和
| (2.21) |
で表される![]() をトラスの不静定次数と呼ぶ。
をトラスの不静定次数と呼ぶ。
例えば,この図-2.56(c)の構造が図-2.56(a)の
ように支持されて載荷された右図のような構造の軸力を
求めてみよう。![]() ,
, ![]() なので
なので![]() となり1次の不静定構造である。
外的には静定なので,反力は
となり1次の不静定構造である。
外的には静定なので,反力は![]() ,
, ![]() ,
, ![]() のように求められる。
部材には1から6の数字を付けて各軸力を
のように求められる。
部材には1から6の数字を付けて各軸力を![]() (
(![]() )とする。
節点法で軸力を求めようとすると
)とする。
節点法で軸力を求めようとすると
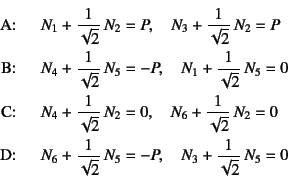
となる。右辺が零の式から
となるので,これを残りの式に代入すると,実はすべての式が同じ
になってしまい,条件式が一つ足りず,軸力を求めることができない。 さてどうしたらいいだろう。
梁の場合も,図-2.58の梁のように支点が三箇所に なると,各支点における反力をつり合いのみからは求めることができない。 つまりこの問題の場合には未知の支点反力が三つあるのに, この面内の鉛直方向の力のつり合いと モーメントのつり合いとの二つしか条件が無いため, 条件が一つ不足してしまうからだ。 したがって断面力も求めることができない。 これはトラスの場合の定義を用いると,外的不静定な構造になっており, 代表的な不静定梁の例である。
ここで少し問題を簡単にするために,図-2.59に
示したように棒は変形しない剛なものと考え,その代わり,
支点にバネ係数![]() あるいは
あるいは![]() を
持つ線形バネを挟んでおいて,どのようにしたら三つの支点反力を
求めることができるか考えてみよう。
まずそれぞれの支点反力を
を
持つ線形バネを挟んでおいて,どのようにしたら三つの支点反力を
求めることができるか考えてみよう。
まずそれぞれの支点反力を![]() ,
, ![]() ,
, ![]() と置いて
と置いて![]() 方向の
力のつり合い条件を表すと
方向の
力のつり合い条件を表すと
となり,一方,左端支点回りの反時計回り方向のモーメントの
つり合い条件は
である。 確かにこれだけでは条件が不足しており反力を求めることはできない。
そこでこの支点にはバネが挟んであることを考えると,支点上の剛な
棒はそれぞれ![]() 方向に沈下していることがわかる。この
方向に沈下していることがわかる。この![]() 方向の
各支点の沈下量を
方向の
各支点の沈下量を![]() ,
, ![]() ,
, ![]() とすると,線形バネであるため,
それぞれの支点反力と沈下量は
とすると,線形バネであるため,
それぞれの支点反力と沈下量は
という関係を持たなければならない。これで条件式が三つ増えたが,未知数と しての支点沈下量もさらに三つ加わったため,まだ一つ条件が不足して いる。実は不足している条件は,この棒が剛であることから得ることができる 幾何学的なものである。
つまり,外力![]() が作用する前にまっすぐだった剛な棒は,載荷後に
支点が沈下したあともまっすぐのままでなければならないという幾何学的
な整合性をまだ考慮していないことに気付く。
この条件は,例えば,左の二つの支点間の棒の傾きが右の二つの支点間の
それに等しいという条件式で表すことができる。
つまり
が作用する前にまっすぐだった剛な棒は,載荷後に
支点が沈下したあともまっすぐのままでなければならないという幾何学的
な整合性をまだ考慮していないことに気付く。
この条件は,例えば,左の二つの支点間の棒の傾きが右の二つの支点間の
それに等しいという条件式で表すことができる。
つまり
でなければならない。 これで,六つの未知数に対して六つの条件式を得たから,問題は解ける はずである。
式(![]() )を式(
)を式(![]() )に代入すると
)に代入すると
となるから,式(![]() ) (
) (![]() )と合わせて
連立方程式にすると
)と合わせて
連立方程式にすると
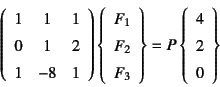
となるため,最終的に支点反力を
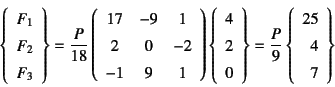
と得る。
これを式(![]() )に代入すれば,支点沈下量が
)に代入すれば,支点沈下量が
と求められる。
この簡単な例のように,力のつり合い条件だけでは解けない
構造を不静定構造
と呼んでいる。不静定構造の解析に当たっては,式(![]() )で
与えたような変形できる構造部材の変形と抵抗力の関係と,
式(
)で
与えたような変形できる構造部材の変形と抵抗力の関係と,
式(![]() )で示したような変形(この場合は剛棒だったので,
棒全体の傾きであったが)と変位(沈下量)の関係とが,
つり合い条件式以外に
必要となる。このように,変形できる物体の力学は
)で示したような変形(この場合は剛棒だったので,
棒全体の傾きであったが)と変位(沈下量)の関係とが,
つり合い条件式以外に
必要となる。このように,変形できる物体の力学は
の三つの条件を同時に満足する数理問題として表される。 トラスや梁も変形することによって抵抗する構造系なので, 同様に三つの条件でその挙動は支配されることになるはずだが, まず次の章では一般論としての変形できる物体の支配方程式を 列挙する。
ちょっと公式: 33の 行列
の逆行列 は次のようにして求めることができる。
ここで行列式は, 3
3の行列の場合は例のたすき掛け式で求めることができる。 また,余因子行列 は
を並べた行列である。計算したい要素と対角の 位置をかなめとする行と列を隠すことと,符号が一つおきに変わることとに 注意する。もちろん,上の公式はサイズに依存しないが,手で計算できる のはくらいが限度であろう。また
の場合には もっと簡単で
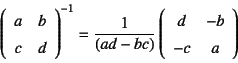
となる。