![\includegraphics[clip]{equili-1.ps}](s1img92.gif)
![\includegraphics[clip]{equili-2.ps}](s1img93.gif)
|
最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
構造力学は変形できる物体の力学だと述べたが,その変形を取り扱う前に,
この章では重要な概念「抵抗力」を導入する。
物体内部の力なので「内力」と総称するが,人間の病気への抵抗力と同様
目に見えない内部の力なのでわかり難い。
だがそれは力には他ならないので,まずその力が満足すべき法則について
書いておこう。
さて我々は,Newtonの運動方程式が正しいものだと考えていいだろう。
あるいはそれが成立するような場のみを対象としている。
そうすると,写真-2.1(a)にあるような力を
受けているstarshipは,
例えば力![]() 方向の移動量を
方向の移動量を![]() としたときに,運動方程式
としたときに,運動方程式
(2.1)
を満足する運動をすることになる。
ここに![]() は時刻である。
は時刻である。![]() はstarshipの
密度で,starshipの体積
はstarshipの
密度で,starshipの体積![]() 上で
密度を積分した
上で
密度を積分した![]() はstarshipの全質量
である。
もしこの物体が静止しているなら,上式の右辺は零になるため,
結局この物体に働いている力は
はstarshipの全質量
である。
もしこの物体が静止しているなら,上式の右辺は零になるため,
結局この物体に働いている力は
| (2.2) |
を満足しなけれがならない。これが力のつり合いである。 ただ注意しなければならないのは,「力がつり合っている状態」が 常に「静止した状態」とは限らないということである。すなわち, 式(2.1a)の左辺が零の場合には加速度が零になるだけなので, このstarshipは等速度運動をしていればよく,静止している必要は無い。 容易に推測できるように,この二つの力に対して適切に固定されていない, 宇宙空間のstarshipのような場合には, この物体は運動し続けるという答も持っていることになる。
さて,では写真-2.1(b)にあるように,
もし二つの力の作用線が同一線上には無い場合を考えてみよう。
もし![]() であれば力はつり合っていることになるが,もちろん,
この物体が回転することは容易に想像できるだろう。
それは,
であれば力はつり合っていることになるが,もちろん,
この物体が回転することは容易に想像できるだろう。
それは,![]() の大きさの偶力
がこの物体には作用しており,その力がこの物体を
反時計回りに回転させてしまうからである。
すなわち,「つり合い状態」を規定するには力のつり合いだけでは
不十分であり,回転に関する運動に関連したつり合いも規定する必要がある。
の大きさの偶力
がこの物体には作用しており,その力がこの物体を
反時計回りに回転させてしまうからである。
すなわち,「つり合い状態」を規定するには力のつり合いだけでは
不十分であり,回転に関する運動に関連したつり合いも規定する必要がある。
例えば,写真-2.2にあるように,
ある点Oから三つの力![]() ,
, ![]() ,
, ![]() の作用線までの
距離をそれぞれ
の作用線までの
距離をそれぞれ![]() ,
, ![]() ,
, ![]() とすると,starshipのO点回りの
反時計方向の回転移動量を
とすると,starshipのO点回りの
反時計方向の回転移動量を![]() としたときに,
そのstarshipは回転の運動方程式
としたときに,
そのstarshipは回転の運動方程式
| (2.3) |
を満足する運動をすることになる。
ここに![]() はstarshipのO点まわりの慣性モーメント
で
はstarshipのO点まわりの慣性モーメント
で
| (2.4) |
と定義される。ここに![]() は点Oから物体中の点までの距離である。
したがって,静止した物体の力学の場合は,
このNewtonの運動方程式の右辺は零になり,この物体に働いている力は
は点Oから物体中の点までの距離である。
したがって,静止した物体の力学の場合は,
このNewtonの運動方程式の右辺は零になり,この物体に働いている力は
を満足しなけれがならない。これがモーメントのつり合いである。
ここまでは簡単のために2次元で,
かつ力の向きを限定した上でつり合い式を導いた。
もし2次元での一般的な図-2.3のような場合には,
力のベクトル![]() と作用点までの位置ベクトル
と作用点までの位置ベクトル![]() の
の![]() ,
, ![]() 方向
成分同士で上述のようなつり合いを考えれば簡単である。
つまり,
方向
成分同士で上述のようなつり合いを考えれば簡単である。
つまり,![]() ,
, ![]() 方向の力の成分を添え字
方向の力の成分を添え字![]() ,
, ![]() で表すことにすれば,
そのつり合いはそれぞれ
で表すことにすれば,
そのつり合いはそれぞれ
になるということは,容易に理解できるであろう。
また原点O回りの反時計回りのモーメントのつり合いは,
例えば,![]() と
と![]() を図中で
を図中で![]() ,
, ![]() 成分に分解して
各自鉛筆で図示しておき,
その二つの力成分の反時計回りのモーメントを考えてみるとわかるように
成分に分解して
各自鉛筆で図示しておき,
その二つの力成分の反時計回りのモーメントを考えてみるとわかるように
となる。 この二つのつり合い式を3次元に一般化し, 成分ではなくベクトルそのもので表現すると,それぞれ
(2.5)
と表されることも理解できるだろう。ここに![]() はベクトル積
(あるいは外積
)をとる。
もちろん,この式(2.5)は3次元の場合も成り立つ。
では原点回りの式(2.5b)同様,任意の点A回りの
モーメントについてもつり合っているかどうか確かめてみよう。
点Aの位置ベクトルを
はベクトル積
(あるいは外積
)をとる。
もちろん,この式(2.5)は3次元の場合も成り立つ。
では原点回りの式(2.5b)同様,任意の点A回りの
モーメントについてもつり合っているかどうか確かめてみよう。
点Aの位置ベクトルを![]() と
すると,その回りのモーメントの総和は
と
すると,その回りのモーメントの総和は
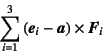
であるから,次のように展開すれば
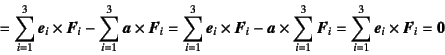
になるのは理解できるだろう。
力のつり合い
![]() から三つ目の等号が
成立し,O点回りのモーメントのつり合い
から三つ目の等号が
成立し,O点回りのモーメントのつり合い
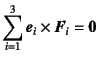 から四つ目の等号が
成立するからである。
したがって,物体が適切に固定2.2され,
そこに作用している力が式(2.5)を満足しているとき,
その物体はつり合い状態にあると呼ぶ。
から四つ目の等号が
成立するからである。
したがって,物体が適切に固定2.2され,
そこに作用している力が式(2.5)を満足しているとき,
その物体はつり合い状態にあると呼ぶ。
以上,暗黙のうちに力![]() は物体の外から作用しているものに限定していた。
このような,物体にとって外の環境から作用する力を外力
と呼ぶ。
そこで図-
は物体の外から作用しているものに限定していた。
このような,物体にとって外の環境から作用する力を外力
と呼ぶ。
そこで図-![]() で紹介したトラス橋の1パネルを
模擬し,3本の部材
(太い線はある太さを持った棒)から成る
構造を図-2.4に示した。
点A, B, Cは格点
と呼ばれ,そこに集まる部材同士がまっすぐのまま
自由に回転できるように接続されていると考えて欲しい。
実際にはピンや比較的柔らかい板で接合されている。
上の格点Cに作用しているのが外力
で紹介したトラス橋の1パネルを
模擬し,3本の部材
(太い線はある太さを持った棒)から成る
構造を図-2.4に示した。
点A, B, Cは格点
と呼ばれ,そこに集まる部材同士がまっすぐのまま
自由に回転できるように接続されていると考えて欲しい。
実際にはピンや比較的柔らかい板で接合されている。
上の格点Cに作用しているのが外力![]() ,
, ![]() である。
このとき下の二つの格点は沈下しないように支えられており,
このような通常の支持構造を三角形の記号で描くことが多い。
ただ左側Aは三角形記号だけだが,右側Bはその記号の下に線分が描かれている。
これは,左の支持は上下方向だけではなく水平方向にも固定されていることを示し,
右の支持は水平方向には移動可能であることを表している。
右のような支持を,三角形ではなく円で表すこともある。
である。
このとき下の二つの格点は沈下しないように支えられており,
このような通常の支持構造を三角形の記号で描くことが多い。
ただ左側Aは三角形記号だけだが,右側Bはその記号の下に線分が描かれている。
これは,左の支持は上下方向だけではなく水平方向にも固定されていることを示し,
右の支持は水平方向には移動可能であることを表している。
右のような支持を,三角形ではなく円で表すこともある。
二つの外力を受けたこの構造は,その力を部材が伝達し,
支持された2点A, Bで地盤にその力を逃がすことによって外力を支えている。
つまり,作用反作用の原理
で地盤は構造をこの2点で支えていることになる。
したがって,動かない構造は支持点で地盤から力を受けて,
地盤に支えられていると考えればいいことになる。
このような力を反力
と呼んでいる。図の![]() ,
, ![]() ,
, ![]() がその反力である。
支点Bは水平方向への移動が自由なので,水平方向の反力は生じない。
このような反力は,構造にとっては外から作用している力とは区別がつかないので,
外力として扱えばいいことになる。
がその反力である。
支点Bは水平方向への移動が自由なので,水平方向の反力は生じない。
このような反力は,構造にとっては外から作用している力とは区別がつかないので,
外力として扱えばいいことになる。
この三つの支点反力の大きさは前節で説明したつり合い条件で
求めることができる。![]() ,
, ![]() 方向の力のつり合いと,
点A回りの反時計回りのモーメントのつり合いは
方向の力のつり合いと,
点A回りの反時計回りのモーメントのつり合いは
となる。この3式から反力は
のように求めることができる。 支持構造と地盤はこの大きさの力を支えることができないといけないことになる。 ただ,反力を求めただけでは,この構造自体が壊れないように 設計されているかどうかはわからない。つまり,部材が 外力を「伝達」するところで何が起こっているのか調べない限り, 構造自体の挙動は把握できず,構造の設計はできないことになる。
さて前節では,点Cで受けた外力を部材が支点へと伝達すると述べたが,
それはどういう仕組みだろうか。章-![]() にも書いた通り,
この文書で取り扱うのは変形できる物体の力学である。
つまり,ここで例として扱っている3本の部材でできた構造も,
実は外力の作用に対して図-2.5に模式的に描いたように,
それぞれの部材が伸び縮みしてつり合い状態になっているのである。
わかり易いように,この図-2.5では
各部材をバネで置き換えてある。少し誇張して描いたが,
支持点Aは動かず,点BはB'の位置に,点CはC'の位置に移動している。
ここで各バネが例えば
にも書いた通り,
この文書で取り扱うのは変形できる物体の力学である。
つまり,ここで例として扱っている3本の部材でできた構造も,
実は外力の作用に対して図-2.5に模式的に描いたように,
それぞれの部材が伸び縮みしてつり合い状態になっているのである。
わかり易いように,この図-2.5では
各部材をバネで置き換えてある。少し誇張して描いたが,
支持点Aは動かず,点BはB'の位置に,点CはC'の位置に移動している。
ここで各バネが例えば
![]() ,
,
![]() ,
,
![]() だけ伸びていた2.3としよう。
各添え字は部材の両端の記号に対応している。
もし各部材のバネ定数(抵抗係数)がそれぞれ
だけ伸びていた2.3としよう。
各添え字は部材の両端の記号に対応している。
もし各部材のバネ定数(抵抗係数)がそれぞれ![]() ,
,
![]() ,
, ![]() であれば,
それぞれのバネには
であれば,
それぞれのバネには
![]() ,
,
![]() ,
,
![]() の
大きさの抵抗力2.4が発生していることになる。
この抵抗力を内力
と呼んでいる。
例えば材料がスポンジだと,小さい抵抗力しか発揮できない。
つまりバネ定数が小さくて,ちょっとした力で大きな変形が生じ,
その変形が限度を超えると壊れてしまう。もし材料が鋼だと,
バネ定数が大きいことから大きな抵抗力を発揮でき,大きな外力を
伝達することができ,部材に生じる変形も
小さい状態に留めることができる。その材料特有の破壊の限界としての
変形の限界に相当して,
対応する内力にも限界(「強度」
)があることになる。
このように,「内力」が,部材を構成している材料の「強度」を超えてしまうと,
構造は崩壊(破壊)してしまうことになるので,
内力は設計における最も重要な量の一つである。
の
大きさの抵抗力2.4が発生していることになる。
この抵抗力を内力
と呼んでいる。
例えば材料がスポンジだと,小さい抵抗力しか発揮できない。
つまりバネ定数が小さくて,ちょっとした力で大きな変形が生じ,
その変形が限度を超えると壊れてしまう。もし材料が鋼だと,
バネ定数が大きいことから大きな抵抗力を発揮でき,大きな外力を
伝達することができ,部材に生じる変形も
小さい状態に留めることができる。その材料特有の破壊の限界としての
変形の限界に相当して,
対応する内力にも限界(「強度」
)があることになる。
このように,「内力」が,部材を構成している材料の「強度」を超えてしまうと,
構造は崩壊(破壊)してしまうことになるので,
内力は設計における最も重要な量の一つである。
このような内力は材料が変形することによって生じているものなので,
構造全体を眺めている図-2.4等に矢印では
描くことができない。
これを見えるようにするには(頭の中で)部材を切断してみればいい。
切断したため材料の内部が見えてしまうので,
その部材の切断面に内力が生じているように見えることになる。
点Cの近傍で二つの部材を切断してみたのが図-2.6である。
切断した相対する断面には作用反作用の原理
に従って,
同じ内力が逆向きに生じていると考えればいい。
慣例として「切断面の外向きの力(引張り)を正と考えて矢印で描く」ことに
なっている。
内力が圧縮の場合は,逆向きの力なのでその値が負になる。
この内力を求めるためには,
例えば切り離してしまった点Cにおいて,二つの外力![]() ,
, ![]() と
二つの内力
と
二つの内力![]() ,
, ![]() との四つの力の
との四つの力の![]() ,
, ![]() 方向の
力のつり合いを考えればいいことになる。
切断したことによって内力を(頭の中では)外力と同じように
扱うことができるので,
内力と外力のつり合い条件を用いて内力を求めることができる。
詳細な定義は後述するが,
この例のように,
つり合い条件のみで反力のみならず内力も求めることができる
構造系を静定な
構造系と呼んでいる。
方向の
力のつり合いを考えればいいことになる。
切断したことによって内力を(頭の中では)外力と同じように
扱うことができるので,
内力と外力のつり合い条件を用いて内力を求めることができる。
詳細な定義は後述するが,
この例のように,
つり合い条件のみで反力のみならず内力も求めることができる
構造系を静定な
構造系と呼んでいる。
このように, 我々が構造設計をする際に必要な重要情報の一つは内力であり, それは力学的な原理によって求めることができる。 したがって,内力という概念と力学原理が理解できない場合には, この文書は多分全く理解できないだろうし,社会基盤構造のデザインはできない。 次の節からは,最も基本的な社会基盤構造形態であるトラスと梁を対象として, 力学原理を用いて内力分布を求めてみる。