 |
�ŐV�ł𐳊m�ɓǂޏꍇ�ɂ� pdf �t�@�C�� ���ǂ����B����� web �����̂��߂̊ȈՋ��łł��B
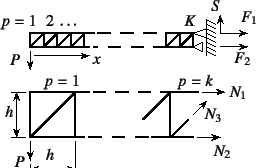
���悢��C��-![]() �̍ŏ��Ɍ����u���v�̗͊w��
�l���悤�B�}-2.28�Ɏ������̂́C
�N���[���̃A�[���\���̂悤��
�ג����g���X�\���ł���B
�S����
�̍ŏ��Ɍ����u���v�̗͊w��
�l���悤�B�}-2.28�Ɏ������̂́C
�N���[���̃A�[���\���̂悤��
�ג����g���X�\���ł���B
�S����![]() �̎l�p�p�l��(
�̎l�p�p�l��(![]() )���琬��C
��[�ɉd
)���琬��C
��[�ɉd![]() ����p���Ă���B
�܂����͂����߂�ƁC
����p������B
�܂����͂����߂�ƁC![]() ,
, ![]() �����̗͂̂荇���ƁC
��[��
�����̗͂̂荇���ƁC
��[��![]() �̍ډד_�ł̃��[�����g�̂荇����
�̍ډד_�ł̃��[�����g�̂荇����
�ƂȂ�̂ŁC![]() ,
, ![]() �Ƌ��߂���B
���ɒf�ʖ@��p���đ�
�Ƌ��߂���B
���ɒf�ʖ@��p���đ�![]() �p�l���Őؒf���C�㉺���ނƎނ̎��͂����ꂼ��
�p�l���Őؒf���C�㉺���ނƎނ̎��͂����ꂼ��![]() ,
,
![]() ,
, ![]() �Ƃ��āC�荇�����Ƃ��
�Ƃ��āC�荇�����Ƃ��
�ƂȂ�B���������[�����g�̂荇���́C![]() �̍ډד_�łƂ����B
���������āC�e���ނ̎��͂�
�̍ډד_�łƂ����B
���������āC�e���ނ̎��͂�
�Ƌ��߂���B
�����ނ́C�[����2�{�̎��͂���2.8�ŁC����ȊO�͂��ׂ�![]() �ł���B
�ł���B
�ł́C�}-2.28�Ɏ������ג����g���X���C
���̂��ꂼ��̌��ނ������Ȃ����炢�������璭�߂Ă݂�ƁC
���͍ג����_��![]() ���x���Ă���悤�Ɍ�����B
��������ƁC�E�[�̎x�_���͂�}-2.29�̉E�}�̂悤��
�����邱�Ƃ��ł��������B
�܂�C���̏ꍇ��
���x���Ă���悤�Ɍ�����B
��������ƁC�E�[�̎x�_���͂�}-2.29�̉E�}�̂悤��
�����邱�Ƃ��ł��������B
�܂�C���̏ꍇ��![]() �����ɂ͉d�������Ă��Ȃ��̂ŁC
�����ɂ͉d�������Ă��Ȃ��̂ŁC![]() �����̔��͂�
���R
�����̔��͂�
���R
![]() �ł��邪�C����ȊO��
�ł��邪�C����ȊO��![]() ����������
����������![]() �ƁC
�}�ɕ`�����悤�Ȕ����v�������̓��[�����g
�ƌĂ��
�ƁC
�}�ɕ`�����悤�Ȕ����v�������̓��[�����g
�ƌĂ��![]() ���C���̍ג����_���Œ肷�邽�߂�
���͂Ƃ��ĕǂ̑��ɔ�������ƍl����̂ł���B
���������́u���́v
���C���̍ג����_���Œ肷�邽�߂�
���͂Ƃ��ĕǂ̑��ɔ�������ƍl����̂ł���B
���������́u���́v![]() ��
��![]() �C�܂��u���̓��[�����g�v
�C�܂��u���̓��[�����g�v![]() �Ƃ����T�O��
�Ƃ����T�O��
�ɂȂ��Ă���B
���ɁC���̔��͂̍l�����ɍ��킹�āC
�g���X�̔C�ӂ̈ʒu![]() �ɒf�ʖ@�Őؒf����ꂽ�ꍇ�ɁC3�{
�̃g���X���ނ̌X�̒f�ʗ͂ł͂Ȃ��C���̈ʒu
�ɒf�ʖ@�Őؒf����ꂽ�ꍇ�ɁC3�{
�̃g���X���ނ̌X�̒f�ʗ͂ł͂Ȃ��C���̈ʒu![]() �̒f�ʗ͂�
���a�Ƃ��Ă̓��͂�V������`���邱�Ƃɂ���B
���ꂪ�}-2.30�Ɏ�������̒f�ʗ́C����f��
�̒f�ʗ͂�
���a�Ƃ��Ă̓��͂�V������`���邱�Ƃɂ���B
���ꂪ�}-2.30�Ɏ�������̒f�ʗ́C����f��
![]() ���Ȃ����[�����g
���Ȃ����[�����g
![]() �ł���B�O�҂͂���قǓ���Ȃ��Ǝv�����C
��҂͉E�[�́u���̓��[�����g�v�ɍ��킹�����̂ł���B
�}�̊w�I�ȊW����
�ł���B�O�҂͂���قǓ���Ȃ��Ǝv�����C
��҂͉E�[�́u���̓��[�����g�v�ɍ��킹�����̂ł���B
�}�̊w�I�ȊW����
�ƒ�`�ł���B������![]() ����
����![]() �p�l���̓r���ł����
�p�l���̓r���ł����
�Ȃ̂ŁC�ŏI�I�ɂ��̎��Ə㎮(![]() )��
)��![]() ,
,
![]() ,
, ![]() �Ƃ��㎮�ɑ������C����f�͂ƋȂ����[�����g��
�Ƃ��㎮�ɑ������C����f�͂ƋȂ����[�����g��
�Ƌ��߂���B
�܂�}-2.30�̈�ԉ��ɂ���悤�ɁC
�ג����_�łł����\�����Ȃ���ꂽ�ꍇ�ɂ́C
�f�ʂɔ��������R�́i���́j�͒P���Ȏ��͂ł͂Ȃ��C
���̐}�̂悤�Ɂu����f�́v�ƌĂ��_�̎��ɒ�����������̒f�ʗ͂ƁC
�f�ʂɐ����Ă������2.9�܂�u�Ȃ����[�����g�v�̓�ł����
�l���Ȃ���Ȃ�Ȃ����ƂɂȂ�B
���Ȃ݂ɁC���̓�̒f�ʗ͂��C
�ؒf�����f�ʂɂ�p.![]() ��
�������u�ؒf�̖v������悤�ɁC���݂��ɋt�����œ����傫����
�f�ʗ͂���p�����Ȃ���Ȃ�Ȃ��B
�ؒf�����f�ʂ̊O�����@���x�N�g����
��
�������u�ؒf�̖v������悤�ɁC���݂��ɋt�����œ����傫����
�f�ʗ͂���p�����Ȃ���Ȃ�Ȃ��B
�ؒf�����f�ʂ̊O�����@���x�N�g����![]() �����̖ʂ����̖�
�ƌĂԂ��C���K�Ƃ��āC���̖ʂɍ�p����
�����̖ʂ����̖�
�ƌĂԂ��C���K�Ƃ��āC���̖ʂɍ�p����![]() �̕������̂���f�͂�
���Ƃ��C�����v����̋Ȃ����[�����g�𐳂Ƃ���B
����ɑ��āC�ؒf�������Α��̖ʁC�܂�f�ʂ̊O�����@���x�N�g����
�̕������̂���f�͂�
���Ƃ��C�����v����̋Ȃ����[�����g�𐳂Ƃ���B
����ɑ��āC�ؒf�������Α��̖ʁC�܂�f�ʂ̊O�����@���x�N�g����![]() ������
�t�����̖ʂ����̖�
�ƌĂсC����f�͂�
������
�t�����̖ʂ����̖�
�ƌĂсC����f�͂�![]() ���̐������𐳁C�Ȃ����[�����g�͎��v����
���Ƃ���B��-
���̐������𐳁C�Ȃ����[�����g�͎��v����
���Ƃ���B��-![]() �̃X�|���W�̎ʐ^�ŁC
���̒��ɐ�������͂Ƃ��ċȂ����[�����g���Љ�����C
���̐߂ł̐����ł��̗͊w�I��`�������ł���C
������{�I�ȍ\���͊w��8���ڂ܂œ��B���������R�ł���B
���������̍ŏ��̓���ǂ���ł���B
�̃X�|���W�̎ʐ^�ŁC
���̒��ɐ�������͂Ƃ��ċȂ����[�����g���Љ�����C
���̐߂ł̐����ł��̗͊w�I��`�������ł���C
������{�I�ȍ\���͊w��8���ڂ܂œ��B���������R�ł���B
���������̍ŏ��̓���ǂ���ł���B
�O�߂̂悤�ɁC�ג����_�����d
�i�_�̎����ɒ�����������ւ̉d�j���C
�Ȃ����Ďx����\�����ނ���
�ƌĂԁB
���̂Ƃ��C���̒f�ʂɂ�����f��
���Ȃ����[�����g
�Ƃ������͂������Ē�R����̂ł���B�}-2.31�̂悤��
�В[�����ȕǂɌŒ肳�i���ߍ��܁j��C�В[�����R��
�ړ��ł�������Ў�����
�ƌĂ�ł���B�f�ʂ́C��-![]() �ŗ�ɗp�����X�|���W��
�悤�ɒ����`�f�ʂł�������C�包��[���̂悤��I�`�f�ʓ��ł���B
�ŗ�ɗp�����X�|���W��
�悤�ɒ����`�f�ʂł�������C�包��[���̂悤��I�`�f�ʓ��ł���B
�f�ʗ͂����߂�ɂ́C�g���X�Ɠ��l�C�f�ʂ����z�I�ɐؒf����K�v������B
�������g���X�Ƃ͈قȂ�C1���ޒ��ł����Ă��f�ʗ͂͏ꏊ�ɂ���ĈقȂ邽�߁C
�ꏊ�̊��ƂȂ���ł͂Ȃ��B���������āC�f�ʖ@��p����̂��K�ł��낤�B
�����ō��[����![]() �̈ʒu�ɐؒf�ʂ����C�}-2.31�̉E�}�̂悤��
�f�ʗ͂𐳂��������Őݒ肵�C���̐ؒf�ʂ�荶���ł̂荇�����Ƃ��
�̈ʒu�ɐؒf�ʂ����C�}-2.31�̉E�}�̂悤��
�f�ʗ͂𐳂��������Őݒ肵�C���̐ؒf�ʂ�荶���ł̂荇�����Ƃ��
�ƂȂ�B���[�����g�͐ؒf�ʂ̉��łƂ����B���������āC�f�ʗ͂�
�ƂȂ�C�㎮(![]() )�ƈ�v����B
���߂�ꂽ���̒f�ʗ͂̌��ʂ�}-2.32��
�������B���ꂼ�������f�͐}
������Ȃ����[�����g�}
�ƌĂсC�O�҂͏�����𐳂ɁC��҂͉������𐳂ɂƂ�2.10���Ƃ������B
�Ȃ�����ȍ~�C����1�{�̐��ŕ`���C�f�ʂ̌`����̓I�ɂ͎����Ȃ��ꍇ�������B
�������C��������ƕ����������f�ʂ̖_�ł��邱�Ƃ��C��ɖY��Ȃ��ŗ~�����B
)�ƈ�v����B
���߂�ꂽ���̒f�ʗ͂̌��ʂ�}-2.32��
�������B���ꂼ�������f�͐}
������Ȃ����[�����g�}
�ƌĂсC�O�҂͏�����𐳂ɁC��҂͉������𐳂ɂƂ�2.10���Ƃ������B
�Ȃ�����ȍ~�C����1�{�̐��ŕ`���C�f�ʂ̌`����̓I�ɂ͎����Ȃ��ꍇ�������B
�������C��������ƕ����������f�ʂ̖_�ł��邱�Ƃ��C��ɖY��Ȃ��ŗ~�����B
���̏ꍇ�̓g���X�ƈ���āC
�x�Ԃ̂ǂ̈ʒu�ɂ��W���d�͍�p�ł�����̂ƍl����B
�܂����łɍڂ����}-2.19�̂悤�Ȋ��d���C
���̂܂ܗ��ɒ��ڍڂ镪�z�d�ƍl���Ă������ƂɂȂ��Ă���B
���Ɏx�������ɂ��ẮC�O�߂Ŏ�舵�����Ў������̂悤�ɁC
�ǂɖ��ߍ��܂ꂽ�悤�Ȃ��̂ƁC�P���Ɏx���Ă��邾���̂��̂�����B
�x���L���ƁC
���ꂼ��̏ꍇ�̔����\�Ȏx�_���͂�}-2.33�Ɏ������B
�O�p�`�̎x���́C�g���X�̏ꍇ�Ɠ��l�C�O�p�L�������̏ꍇ�͐��������ɂ�
�Œ肳��Ă��邱�Ƃ���C�d�ɂ���Ă͐�������![]() ��������B
�O�p�L���̉��ɐ���������ꍇ�́C���������͎��R�Ɉړ��\�ł���C
�������͂͐����Ȃ��B�Ȃ����͂ƊO�͂́C����������
��������B
�O�p�L���̉��ɐ���������ꍇ�́C���������͎��R�Ɉړ��\�ł���C
�������͂͐����Ȃ��B�Ȃ����͂ƊO�͂́C����������![]() ���̐������𐳂�
��
���̐������𐳂�
��![]() �Ƃ��邪�C���������͏d�͏�ł̎��d�̂��Ƃ�O���ɒu���C
���K�Ƃ���
�Ƃ��邪�C���������͏d�͏�ł̎��d�̂��Ƃ�O���ɒu���C
���K�Ƃ���![]() ���̕��̕����𐳂�
2.11��
���̕��̕����𐳂�
2.11��![]() �Ƃ���B
�܂��O�́i���́j���[�����g
�Ƃ���B
�܂��O�́i���́j���[�����g![]() �ɂ��Ă͔����v���𐳂Ƃ���B
���ߍ��ݒ[�Ŕ��̓��[�����g��������̂́C�O�߂ł̍ג����g���X�̋c�_��
�v���o���Η����ł���ł��낤�B
�ɂ��Ă͔����v���𐳂Ƃ���B
���ߍ��ݒ[�Ŕ��̓��[�����g��������̂́C�O�߂ł̍ג����g���X�̋c�_��
�v���o���Η����ł���ł��낤�B
�}-2.33�̉E�Ɏ������ʐ^�́C ���������̈ړ����Œ肵���P���x�����u�ŁC�s���x�� �ƌĂ�Ă���B����͎ʐ^�̍��ɖ͎��I�ɕ`�����悤�ɁC�s���𒆐S�ɂ��� ������]�ł���悤�ɂȂ��Ă��邽�߁C���̓��[�����g�͐����Ȃ��B �������C���̎ʐ^�̎x���̓Q���o�[���i���z���j�� ���Ԏx�_�Ȃ̂Ő}-2.46�Ɏ����悤�ɁC ���͂̋Ȃ����[�����g����ɂ͂Ȃ�Ȃ����Ƃɂ͒��ӂ���B
�����z�d![]() ����Ў������������Ă݂悤�B
�����ł́C�g���X�̒f�ʖ@�̎菇�Ɠ����悤�ɉ������Ƃɂ���B
����Ў������������Ă݂悤�B
�����ł́C�g���X�̒f�ʖ@�̎菇�Ɠ����悤�ɉ������Ƃɂ���B![]() ��
�������̓����z�d������p���Ă��Ȃ��̂ŁC�܂��x�_���͂́C
����������̔���
��
�������̓����z�d������p���Ă��Ȃ��̂ŁC�܂��x�_���͂́C
����������̔���![]() �Ɣ����v����̔��̓��[�����g
�Ɣ����v����̔��̓��[�����g![]() �����ł���B
�O�͂Ɣ��͂̂荇����
�����ł���B
�O�͂Ɣ��͂̂荇����
�ł��邪�C���[�����g�̂荇���́C�����z�d�����̕��z�̏d�S�C
�܂�X�p������(
![]() )�ɑ���
)�ɑ���![]() ����p�����Ă�
����������
����p������
����������
 �ƍl���Ă��悭�C����
�ƍl���Ă��悭�C����
�Ƌ��߂���B�������ϕ������s���Ă������ł���B
���ɁC���ߍ��ݒ[����![]() �̈ʒu�Œf�ʂ�ؒf���C�����ɐ�����������
�f�ʗ͂���������ŁC���̍����̕����̂荇�����l����B���[�����g��
�ؒf�ʉ��ōl�����
�̈ʒu�Œf�ʂ�ؒf���C�����ɐ�����������
�f�ʗ͂���������ŁC���̍����̕����̂荇�����l����B���[�����g��
�ؒf�ʉ��ōl�����
�ɂȂ�B![]() ��
��![]() �����̐ϕ������邽�߂̃_�~�[�̍��W�ł���B
�ϕ����Ă��������C���͂����߂��Ƃ��Ɠ��l�ɁC���z�d�𑍗͂�
�d�S�ɍ�p�����W���d�Œu���������
�����̐ϕ������邽�߂̃_�~�[�̍��W�ł���B
�ϕ����Ă��������C���͂����߂��Ƃ��Ɠ��l�ɁC���z�d�𑍗͂�
�d�S�ɍ�p�����W���d�Œu���������
�Ƃ��Ă������i�}�����Ȃ��玩���ōl���ė~�����j����C
�㎮(![]() )�������ĉ�����
)�������ĉ�����
�ƁC����f�͂ƋȂ����[�����g�̕��z�����߂���B
���ߍ��ݒ[��O�߂̐ݒ�ƕς������߁C
����f�͂̕������ς���Ă��邱�Ƃɒ��ӂ���B
�Ƃ���ŁC�O�߂̎�(![]() )�̏ꍇ�������ł��������C
�㎮(
)�̏ꍇ�������ł��������C
�㎮(![]() )�̏ꍇ��
)�̏ꍇ��
���������邱�Ƃ͊o���Ă����ė~�����B �܂�C�Ȃ����[�����g�}���킩�����Ƃ��ɂ́C���̌X��������f�͐}�ɂȂ�B
���ɂ́C���[���P���Ɏx������Ă����P����
�ɏW���d����p�����}-2.36�̏ꍇ��ΏۂƂ��Ă݂�B
�܂��x�_���͂����߂邽�߂ɁC���͂ƊO�͂̂荇�����Ƃ��
�Ƌ��߂���B���[�����g�͍��[�̉��łƂ��Ă���B
���ɁC�W���d�̍ډד_��������(
![]() )��
����f�ʂ�ؒf���C�ؒf�ʂ������̕����ł荇�����Ƃ��
)��
����f�ʂ�ؒf���C�ؒf�ʂ������̕����ł荇�����Ƃ��
�ƂȂ邱�Ƃ���C����f�͂ƋȂ����[�����g��
�Ƌ��߂���B����ɑ��C�ډד_�����E���Őؒf�����ꍇ�ɂ́C
�ؒf�ʂ������̕����ł荇�����Ƃ��
�ƂȂ�C����������������C��������}-2.36�̉E�[��
�悤�ɁC�ؒf�ʂ����E�̕����ł荇�����Ƃ��
�ł��邱�Ƃ���C�f�ʗ͂�
�Ƌ��߂���B�}-2.37�Ɍ��ʂ��������B
�P���x���[�͉�]���R�Ȃ��߂ɁC�Ȃ����[�����g�͗�ɂȂ��Ă���B
�܂�����f�͐}�̍ډד_�ł́C�ډd�ʂ�![]() �̑傫�����̕s�A�����ł���B
�̑傫�����̕s�A�����ł���B
���`�ɕ��z����
�d���}-2.38�̂悤�ɍڂ��Ă���ꍇ���l���Ă݂悤�B
���̏ꍇ�̕��z�d��
![]() �ŗ^�����Ă���B
�܂����͂����߂邽�߂ɑS�̂̂荇�����l�����
�ŗ^�����Ă���B
�܂����͂����߂邽�߂ɑS�̂̂荇�����l�����
�ƂȂ�B���z�d�́C�O�p�`�̏d�S�ʒu�ł���
![]() ��
����
��
����
![]() ����p���Ă���悤�ɍl���Ă������B
�㎮���Z�肵�Ĕ��͂����߂��
����p���Ă���悤�ɍl���Ă������B
�㎮���Z�肵�Ĕ��͂����߂��
�ƂȂ�B
���ɍ�����![]() �̈ʒu�̒f�ʂ�ؒf���āC�f�ʗ͂����߂�B�܂��C�荇������
�̈ʒu�̒f�ʂ�ؒf���āC�f�ʗ͂����߂�B�܂��C�荇������
�ƂȂ�B���������āC�f�ʗ͂�
�Ƌ��߂���B���ʂ�}-2.39�Ɏ������B
�Ō�ɁC ���͂������Ē�R������̏ꍇ���l���Ă݂悤�B ��ʂɁC�g���X�̌��ނ̂悤�Ɉ��k�E������Œ�R���镔�ނ��� �ƌĂсC �Ȃ��Ƃ���f�Œ�R���镔�ނ��� �Ə̂��邪�C���̗�����g�ݍ��킹���\�������g 2.12�ƌĂԁB���g�̏ꍇ�́C���ޓ��m�̓s���ł͂Ȃ������i�n�ڂ����悤�ȏ�ԂɁj ����Ă���B��Ƃ��Đ}-2.40���������C �X�p�������Ƃ�������߂ɗ����オ���Ă�����̉��[����������Ă���Ƃ���B
���̍\���ɐ}�������悤�Ȏ߂̊O�͂��ڂ����ꍇ��ΏۂɁC����܂łɂ���� �ؒf�@�����̂܂g���邱�Ƃ������Ă������B �܂��}-2.40�̂悤�ɔ��͂��L���Ă荇�����Ƃ��
�ƂȂ�B���[�����g�͍��[���łƂ����B������
�̂悤�ɋ��߂���B�P���������̍����́C�}�����Ă��Ȃ����C
������![]() �̈ʒu�ɐؒf�����āC
����f�͂ƋȂ����[�����g�ɉ����āC�������̎���
�̈ʒu�ɐؒf�����āC
����f�͂ƋȂ����[�����g�ɉ����āC�������̎���![]() ��
��![]() ������
��p�����Ă荇�����Ƃ邱�Ƃɂ����
������
��p�����Ă荇�����Ƃ邱�Ƃɂ����
�ƂȂ�B���l�ɁC�E���͉E�[����![]() �̈ʒu�ɐؒf�����
�̈ʒu�ɐؒf�����
�Ƌ��߂���B
�Ō�ɒ�������E��ɒ���o�����������́C�}-2.40��
���̐}�̂悤�ɗ��̎��������ƒ��p�����ɊO��![]() ��������ŁC
��[���獶������
��������ŁC
��[���獶������![]() �������C�f�ʂ�ؒf���Ă荇�����l�����
�������C�f�ʂ�ؒf���Ă荇�����l�����
�ƂȂ�B�}-2.40�ɔj����t�������� ���̋Ȃ����[�����g�}�i���̂���f�͐}�j���ɂȂ�悤�ɂ��Ă���̂� ���ӂ��ė~�����B ���̌��ʂ�}�������̂��}-2.41�ł��邪�C ����f�͐}�ƋȂ����[�����g�}�ɉ��������͐} �������Ă���B
������C�����ƍ��g�炵�����̂�ΏۂƂ��Ă݂悤�B
��Ƃ��Đ}-2.42�̍��̍\�����������B
����͍��˂̍������H�̒��ɁC�A�N�Z�X�����v
�̂��߂̗���o�������̂��C
������Ɨ��\�����Ò�n�Ń��f�����������̂ł���B
���͂����߂邽�߂ɑS�̂̂荇�����Ƃ��
�ł��邩��C���͂�
�Ƌ��߂���B
![]() ���͍��̒��̊����E�̒��̊�܂ł̎����ɉ��������W�Ƃ���B
���������āC
���͍��̒��̊����E�̒��̊�܂ł̎����ɉ��������W�Ƃ���B
���������āC![]() �����̒��C
�����̒��C![]() ����̗��C
����̗��C![]() ��
�E�̒����ɑ�������B�܂�����o�����͍ډד_����E������
��
�E�̒����ɑ�������B�܂�����o�����͍ډד_����E������![]() �����Ƃ����B
�Ƃ����̂��C����������ɂ͒f�ʗ͉͂��������Ȃ�����ł���B
����o�����͕Ў������Ɠ����Ȃ̂ŁC�ȒP��
�����Ƃ����B
�Ƃ����̂��C����������ɂ͒f�ʗ͉͂��������Ȃ�����ł���B
����o�����͕Ў������Ɠ����Ȃ̂ŁC�ȒP��
�ƂȂ�B���ɍ��̒��̒���o�����܂ł́C��͂�f�ʂ�ؒf���Ă荇�����Ƃ��
�Ƌ��߂���B���̏�ɂȂ�ƁC����o�����̉d���l��������������Ȃ̂�
�ł���B���ɗ��̕����ɂ��Ă����l�̐ؒf������C�荇������
�Ƌ��߂邱�Ƃ��ł���B�E�̒��͊����l���������ȒP�ŁC�ŏI�I��
�ƂȂ�B�f�ʗ͐}�͏ȗ�����B
���ۂ̋���������ƁC�P�a�Ԃł͂Ȃ��C�����̋��r�̏��n���Ă���悤��
������B���������̌a�Ԃ�A�����ēn�������ɂ���ƁC���͕s�Ò�\���ɂȂ�C
�����܂ł̒m���ł͒f�ʗ͂����߂邱�Ƃ͂ł��Ȃ��B
��������-![]() ��
��Ƃ��ċ��������z����5�a�Ԃ̋��ŁC���r�̏������ƘA�����Ă���悤��
�����邪�C�����Ƃ悭�ώ@����ƃQ���o�[�`��
�̋����ł��邱�Ƃ��킩��B
������ȒP�Ȑ}�ɂ����̂��}-2.43�ł���B
���E�����ڂ̃X�p���ɂ��鏬�������́C
�E�̎ʐ^-2.44�̂悤�ɂ���
�ׂ̌��Ɏx�����Ă���̂ł���B
���̎ʐ^�͂��傤�ǐ}-2.43�̓_A�̈ʒu�������Ă���B
�ʐ^�Ɏʂ��Ă��鉜�̎包������킩��悤�ɁC�ȉ~�ň͂����ɑ�������
�����Ɍ��Ԃ��Ă���B�܂肱���œ�̗��͉�����Ă���2.13�̂ł���B
���̎ʐ^�̏ꍇ�́C���̌����E�̌������̑ȉ~�̕����Ŏx���Ă���B
�v�̏ꍇ�́C���̐}-2.43�̉��̐}�̂悤�ɁC
�q���W�Ń��f�������邱�Ƃ��������C
���ۂɂ͂��̎ʐ^�̂悤�ɂ��Ďx�����Ă���B
��
��Ƃ��ċ��������z����5�a�Ԃ̋��ŁC���r�̏������ƘA�����Ă���悤��
�����邪�C�����Ƃ悭�ώ@����ƃQ���o�[�`��
�̋����ł��邱�Ƃ��킩��B
������ȒP�Ȑ}�ɂ����̂��}-2.43�ł���B
���E�����ڂ̃X�p���ɂ��鏬�������́C
�E�̎ʐ^-2.44�̂悤�ɂ���
�ׂ̌��Ɏx�����Ă���̂ł���B
���̎ʐ^�͂��傤�ǐ}-2.43�̓_A�̈ʒu�������Ă���B
�ʐ^�Ɏʂ��Ă��鉜�̎包������킩��悤�ɁC�ȉ~�ň͂����ɑ�������
�����Ɍ��Ԃ��Ă���B�܂肱���œ�̗��͉�����Ă���2.13�̂ł���B
���̎ʐ^�̏ꍇ�́C���̌����E�̌������̑ȉ~�̕����Ŏx���Ă���B
�v�̏ꍇ�́C���̐}-2.43�̉��̐}�̂悤�ɁC
�q���W�Ń��f�������邱�Ƃ��������C
���ۂɂ͂��̎ʐ^�̂悤�ɂ��Ďx�����Ă���B
�ł͐}-2.45��3�a�Ԃ̃Q���o�[���������Ă݂悤�B
�܂��C�������Ŏx����ꂽ�P������ԁi�ȉ~�ň͂����j�́C����̐}�̂悤��
�����z�d����P�����Ȃ̂ŁC���K���2-3�̖��4��
�i�����ł܂������Ă��������j�œ��͋��߂��Ă���B
���E�̃X�p�����������߂�
�K�v�Ȃ̂͗��[�̔���![]() ,
, ![]() �ł��邪�C
������ȒP��
�ł��邪�C
������ȒP��
![]() �Ƌ��߂���Ǝv���B
�����X�p���́C���[����
�Ƌ��߂���Ǝv���B
�����X�p���́C���[����![]() �����`����ƁC�f�ʗ͂�
�����`����ƁC�f�ʗ͂�
�ƂȂ�B���ꂪ���߂�ꂽ���Ƃ́C ���E�̒���o���X�p���܂ł̋�Ԃ����ꂼ��C��������� �E���̐}�̂悤�ȕʁX�Ȍn�Ƃ��ĉ������������ł���B
�܂������̌n�̎x�_���͂́C�͂̂荇���ƃ��[�����g�̂荇����������
�ƂȂ�B�����ŁC���[����![]() �����`���č����珇�ɉ����Ă݂�ƁC
�܂�
�����`���č����珇�ɉ����Ă݂�ƁC
�܂�![]() �̊Ԃ�
�̊Ԃ�
�Ƌ��߂���B�����
![]() �܂ł̊Ԃ�
�܂ł̊Ԃ�
�ł���B�Ō�ɒ���o������
![]() �̋�Ԃ�
�̋�Ԃ�
�Ƌ��߂���B
���ɉE�̕����́C�܂����͂�
�Ƌ��߂���B���[����![]() �������C���ɍ���������ƁC
�������C���ɍ���������ƁC![]() �ł�
�ł�
�ƂȂ�B����
![]() �ł�
�ł�
�ł���C
![]() �̋�Ԃł�
�̋�Ԃł�
�Ƌ��߂���B�e���v�Z���Ă݂ė~�����B
�}-2.46�� ���z�}�����������C���ꂼ��̒l��
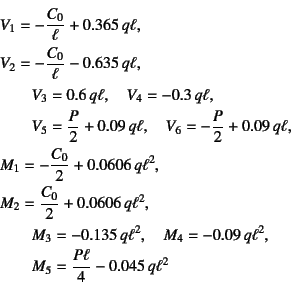
�ł���B�q���W�̕����ŋȂ����[�����g����ɂȂ��Ă��邱�Ƃɒ��ӂ���B ���l�I�ɋߎ��������߂��@����-5�Ő������邪�C ���̕��@��p���Ă܂������ȗ����������߂́C ���҂炪�쐬�����v���O�������d�q�I�� ����\�ɂȂ��Ă���B�}-2.46�̂悤�Ȑ}�̒l���C �p�[�\�i���R���s���[�^ ��Őݒ肵�ċ��߂邱�Ƃ��ł���B�X�p���r���Ƀq���W��o�l�x�����}���ł��邪�C ������@�ɂ��Ă͂܂��������Q�Ƃ̂��ƁB
�܂��C�荇�������������K�����邽�߂ɂ́C����[106]���� �����̖��������ė~�����B
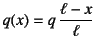 ����p�����C
���[�Œ�̕Ў������̒f�ʗ͐}�����߂�B
����p�����C
���[�Œ�̕Ў������̒f�ʗ͐}�����߂�B
�g���X�̐�-2.2.3 (4)�ŁC
�v�ɕK�v�ȕ����ʂ͒f�ʂ̋��x�C�܂�����
���Əq�ׂ��B���̍ג����g���X�̑�![]() �p�l���̍��[��
�߂��������o�����̂��}-2.48��
����Bp.
�p�l���̍��[��
�߂��������o�����̂��}-2.48��
����Bp.![]() �̎�(
�̎�(![]() )�ŋ��߂��悤�ɁC
�܂��㌷�ނ�
)�ŋ��߂��悤�ɁC
�܂��㌷�ނ�![]() �̈�����̎��͂������Ă��邪�C�Ⴆ��I�`������
�f�ʂɂ́C���̐}�ɕ`�����悤�ɁC��l�ɕ��z����P�ʖʐϓ������
���́i��R�́G���́j�������Ă���B
�܂��ނ���l�ȉ��͂ň������C�����ނ͈��k�Ȃ̂ŁC�Ⴆ�Δ��`��
�����f�ʂɁC���̐}�̂悤�ɁC��͂��l�Ȉ��k���͂������Ă���B
���������āC��-2.2.3 (4)��
�l�����悤�ɁC���̈�l�ȉ��́i��R�́j�����x���Ȃ��悤�ɐv����C
�����Ĉ��S�ȍ\�����v�ł��邱�ƂɂȂ�B
�̈�����̎��͂������Ă��邪�C�Ⴆ��I�`������
�f�ʂɂ́C���̐}�ɕ`�����悤�ɁC��l�ɕ��z����P�ʖʐϓ������
���́i��R�́G���́j�������Ă���B
�܂��ނ���l�ȉ��͂ň������C�����ނ͈��k�Ȃ̂ŁC�Ⴆ�Δ��`��
�����f�ʂɁC���̐}�̂悤�ɁC��͂��l�Ȉ��k���͂������Ă���B
���������āC��-2.2.3 (4)��
�l�����悤�ɁC���̈�l�ȉ��́i��R�́j�����x���Ȃ��悤�ɐv����C
�����Ĉ��S�ȍ\�����v�ł��邱�ƂɂȂ�B
���̒f�ʂ̐v�̏ꍇ�����l�Ȃ͂��Ȃ̂ŁC
�܂����̒f�ʂɐ����Ă��鉞�͕��z��m��K�v�����邪�C
�g���X�قNJȒP�ł͂Ȃ��������B�����ōēx�C�ג����g���X�̗��
�p���Ă݂�B�}-2.48�̂悤�ɁC
�㌷�ނɂ͍��v��![]() �̈�����̎��͂������Ă������ŁC
�����ނɂ͂�͂��l�ȉ��͂�
�̈�����̎��͂������Ă������ŁC
�����ނɂ͂�͂��l�ȉ��͂�![]() �̈��k���́i
�̈��k���́i![]() �̈����莲�́j���C
�����Ďނ�
�̈����莲�́j���C
�����Ďނ�![]() �����ɂ�
�����ɂ�![]() �̈����莲�͂������Ă���B
���������āC�����ނɋ߂����������ł́C�����ނƎނ̎��͂�
���v��
�̈����莲�͂������Ă���B
���������āC�����ނɋ߂����������ł́C�����ނƎނ̎��͂�
���v��![]() �̈��k���́i
�̈��k���́i![]() �̈����莲�́j�������Ă����
�l���Ă������낤�B�܂�C
�������璭�߂��Ƃ��̃g���X�̐ؒf�ʑS�̂���̒f�ʂƂ��đ������Ƃ��ɁC
���̏�[�Ɖ��[�ɂ͓����傫���̓��͂��t�����Ɂi���k�ƈ�����̋t�����Łj
�����Ă���ƍl����̂́C�f���ł͂Ȃ����낤���B
�̈����莲�́j�������Ă����
�l���Ă������낤�B�܂�C
�������璭�߂��Ƃ��̃g���X�̐ؒf�ʑS�̂���̒f�ʂƂ��đ������Ƃ��ɁC
���̏�[�Ɖ��[�ɂ͓����傫���̓��͂��t�����Ɂi���k�ƈ�����̋t�����Łj
�����Ă���ƍl����̂́C�f���ł͂Ȃ����낤���B
���̂��Ƃ���C���̒��ɂ͎����i![]() ���j�����ɋt�����̓��͂������邱�Ƃɂ���āC
�Ȃ����[�����g�Ƃ�����R�͂������Ă�����̂Ɨ\�z�ł���B
�����}�������̂��}-2.49�ł���B
�ʂ����Ē����I�ɕ��z���邩�ǂ����́C���̒i�K�ł͗����ł��Ȃ��Ă����B
���̏ڍׂɂ��Ă͏�-4�Ő�������B
�����ł́C��1���ߎ��Ƃ��Ē����I�ɉ��͕͂��z���Đ������
�l���Ă����ė~�����B
���̂悤�ȉ��͕��z�̍��v���C�f�ʑS�̂̒�R�͂Ƃ��Ă̋Ȃ����[�����g��
�Ȃ��Ă���̂Ȃ�
���j�����ɋt�����̓��͂������邱�Ƃɂ���āC
�Ȃ����[�����g�Ƃ�����R�͂������Ă�����̂Ɨ\�z�ł���B
�����}�������̂��}-2.49�ł���B
�ʂ����Ē����I�ɕ��z���邩�ǂ����́C���̒i�K�ł͗����ł��Ȃ��Ă����B
���̏ڍׂɂ��Ă͏�-4�Ő�������B
�����ł́C��1���ߎ��Ƃ��Ē����I�ɉ��͕͂��z���Đ������
�l���Ă����ė~�����B
���̂悤�ȉ��͕��z�̍��v���C�f�ʑS�̂̒�R�͂Ƃ��Ă̋Ȃ����[�����g��
�Ȃ��Ă���̂Ȃ�
�Ƃ����W�ɂ��邱�Ƃ͗e�Ղɗ����ł���Ǝv���B![]() �͒f�ʐςł���B
�����v���̃��[�����g�𐳂Ƃ��Ă���̂ŁC��q�̃g���X�̏ꍇ�Ƃ�
���k�E�����肪�t�ɂȂ��Ă���C�����
�͒f�ʐςł���B
�����v���̃��[�����g�𐳂Ƃ��Ă���̂ŁC��q�̃g���X�̏ꍇ�Ƃ�
���k�E�����肪�t�ɂȂ��Ă���C�����![]() �̍�p���܂ł�
������
�̍�p���܂ł�
������![]() �Ƃ��Ă���B
�}�̂悤�ɒf�ʂ�����
�Ƃ��Ă���B
�}�̂悤�ɒf�ʂ�����![]() �ŕ�
�ŕ�![]() �̒����`���Ƃ����
�̒����`���Ƃ����
![]() ��
�Ȃ�̂ŁC�ϕ������
��
�Ȃ�̂ŁC�ϕ������
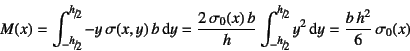
�ƂȂ�B���������āC
�f�ʂ̏㉺���ɔ�������ő剞��![]() �Ɛ����Ă���Ȃ����[�����g
�Ɛ����Ă���Ȃ����[�����g![]() ��
��
�Ƃ����W�ɂȂ�B����![]() ���f�ʌW��
�ƌĂ����̂ŁC�f�ʂ̌`�Ɛ��@�����Ō��܂�ʂł���B
���Ȃ킿�C�g���X�̂悤�ɒf�ʓ��̉��͕��z����l�ȏꍇ�ɂ�
�f�ʂ��w�I�Ȓ�R�W����
�f�ʐ�
���f�ʌW��
�ƌĂ����̂ŁC�f�ʂ̌`�Ɛ��@�����Ō��܂�ʂł���B
���Ȃ킿�C�g���X�̂悤�ɒf�ʓ��̉��͕��z����l�ȏꍇ�ɂ�
�f�ʂ��w�I�Ȓ�R�W����
�f�ʐ�![]() (
(![]() )�����邪�C
����ɑΉ����āC���̋Ȃ��̏ꍇ�̊w�I�Ȓ�R�W����
�f�ʌW��
)�����邪�C
����ɑΉ����āC���̋Ȃ��̏ꍇ�̊w�I�Ȓ�R�W����
�f�ʌW��![]() (
(![]() )�ɂȂ�̂ł���B
�Ȃ��C�����ł�
)�ɂȂ�̂ł���B
�Ȃ��C�����ł�![]() ,
, ![]() ��2���ɑ��đΏ̂Ȓf�ʌ`��̏ꍇ�Ɍ��肵��
�f�ʌW���̒�`�������Ă��邱�Ƃɒ��ӂ��ė~�����B
�C�ӂ̒f�ʌ`�̏ꍇ�͏�-4�Ő������闝�����Q�Ƃ��ė~�����B
��2���ɑ��đΏ̂Ȓf�ʌ`��̏ꍇ�Ɍ��肵��
�f�ʌW���̒�`�������Ă��邱�Ƃɒ��ӂ��ė~�����B
�C�ӂ̒f�ʌ`�̏ꍇ�͏�-4�Ő������闝�����Q�Ƃ��ė~�����B
�g���X�Ɠ����悤�ɁC���̐v�ɓ������Ă��C �v���悤�Ƃ���f�ʂ̉e���������O�ɋ��߂Ă����Ȃ���Ȃ�Ȃ��B ��Ƃ��Đ}-2.50�̒P���v���[�g�K�[�_���l���Ă݂悤�B ���̍��̐}�̈�ԏ�ɂ���̂͂��̃v���[�g�K�[�_�̍������� �͎��}�ł��邪�C �����I�Ȓf�ʂɂ��邽�߂ɁC�X�p��������ԂƂ��̊O����Ԃ��قȂ�f�ʂ� �v���C�}�̒f��A�Őڍ����邱�Ƃɂ����B ��̓I�ȃX�p���̗l�q�͂��̉��Ɏ��������C�f��A��A'���ڍ��ӏ��ŁC ������ԂƂ��̊O���Œf�ʂ̃t�����W���@���� �قȂ�悤�ɐv���悤�Ƃ��Ă���B
�����ł͎x�_�ɋ߂����̌��iB-A��ԁj��
�f�ʂ�v���邱�Ƃ�z�肵�āC
�܂��f��A�ɒ��ڂ��Đv���Ă݂悤�B
���[����![]() �̈ʒu�ɒP�ʏW���d�i�P�ʂ͖����j���ڂ����ꍇ�̒f��A��
�Ȃ����[�����g�Ƃ���f�͂́C���̒f��A�́C���ꂼ��Ȃ����[�����g��
����f�͂̉e����
�ƌĂ��B
�Ȃ����[�����g�}�������߂�Ƃ��Ɠ��l�C���͂����߂Ēf�ʖ@��A�_��
�Ȃ����[�����g�Ƃ���f�͂����߂�Ήe���������߂���B
���̌��ʁC�P�ʂ�m�Ƃ����ꍇ�ɁC
�Ȃ����[�����g�̉e����
�̈ʒu�ɒP�ʏW���d�i�P�ʂ͖����j���ڂ����ꍇ�̒f��A��
�Ȃ����[�����g�Ƃ���f�͂́C���̒f��A�́C���ꂼ��Ȃ����[�����g��
����f�͂̉e����
�ƌĂ��B
�Ȃ����[�����g�}�������߂�Ƃ��Ɠ��l�C���͂����߂Ēf�ʖ@��A�_��
�Ȃ����[�����g�Ƃ���f�͂����߂�Ήe���������߂���B
���̌��ʁC�P�ʂ�m�Ƃ����ꍇ�ɁC
�Ȃ����[�����g�̉e����
![]() �i�P�ʂ�m�j�ƁC����f�͂�
�e����
�i�P�ʂ�m�j�ƁC����f�͂�
�e����
![]() �i�P�ʂ͖����j��
�i�P�ʂ͖����j��
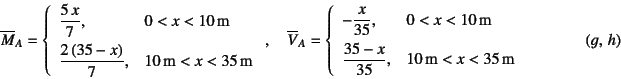
�Ƌ��߂���B�}-2.50��
������
![]() ��
��
![]() ��`���������B
�Ƃ���ŁC�}-2.37�̂���f�͐}��
�Ȃ����[�����g�}�Ƃ̈Ⴂ�ɂ�
�\�����ӂ��邱�ƁB�e�����̉����͒P�ʉd�̍ډʒu�ł���B
���āC�g���X�̏ꍇ�Ɠ��l�ɂ��Ă��̉e������p����C
�f��A���邢�͐v���悤�Ƃ��Ă��鍶�E�̋�Ԃ�
�ł��s���Ɂi�h���j�Ȃ�悤�ȍډʒu������ł���B
���̂Ƃ��ɒ��ڒf�ʂɐ����Ă���ő�̒f�ʗ͂ň��S�ɐv��������B
��`���������B
�Ƃ���ŁC�}-2.37�̂���f�͐}��
�Ȃ����[�����g�}�Ƃ̈Ⴂ�ɂ�
�\�����ӂ��邱�ƁB�e�����̉����͒P�ʉd�̍ډʒu�ł���B
���āC�g���X�̏ꍇ�Ɠ��l�ɂ��Ă��̉e������p����C
�f��A���邢�͐v���悤�Ƃ��Ă��鍶�E�̋�Ԃ�
�ł��s���Ɂi�h���j�Ȃ�悤�ȍډʒu������ł���B
���̂Ƃ��ɒ��ڒf�ʂɐ����Ă���ő�̒f�ʗ͂ň��S�ɐv��������B
�����ł͂܂��C�Ȃ����[�����g��R�ɑ��č��E�̋�Ԃ�v���Ă݂悤�B
�g���X�Ɠ��l�C���z�O��![]() ��
��![]() �̒l�̋��ߕ���
���Ă͐�-A.2�Ɏ������B
�P�����̏ꍇ�C�d���ǂ��ɍڂ낤�Ǝx�_�ł͏�ɋȂ����[�����g��
��ł��邱�Ƃ���C���E��Ԃ̏ꍇ�́C�ł��邾���x�_���牓���f�ʂ�
�Ȃ���R�̈��S���m�ۂ��ׂ��ł��邱�Ƃ͗\�z�ł���Ǝv���B
���������Ēf��A��v��������̂ŁC
�����̋Ȃ����[�����g�̉e����
�̒l�̋��ߕ���
���Ă͐�-A.2�Ɏ������B
�P�����̏ꍇ�C�d���ǂ��ɍڂ낤�Ǝx�_�ł͏�ɋȂ����[�����g��
��ł��邱�Ƃ���C���E��Ԃ̏ꍇ�́C�ł��邾���x�_���牓���f�ʂ�
�Ȃ���R�̈��S���m�ۂ��ׂ��ł��邱�Ƃ͗\�z�ł���Ǝv���B
���������Ēf��A��v��������̂ŁC
�����̋Ȃ����[�����g�̉e����
![]() ��p���āC
�܂��ډʒu�����߂悤�B�}-2.50�̍��Ɏ������悤�ɁC
��(
��p���āC
�܂��ډʒu�����߂悤�B�}-2.50�̍��Ɏ������悤�ɁC
��(![]() )�͎O�p�`���z��
)�͎O�p�`���z��
![]() �ɂȂ�̂ŁC
�}�̉E��Ɏ������悤�ɁC���[���痣�ꂽ����
�ɂȂ�̂ŁC
�}�̉E��Ɏ������悤�ɁC���[���痣�ꂽ����![]() ��
�ʒu����
��
�ʒu����![]() m�̋�Ԃ�
�傫�ڂ̉d
m�̋�Ԃ�
�傫�ڂ̉d![]() ���ڂ����Ƃ����C�f��A�ɂƂ��Ă͍ł��s���ɂȂ�B
���������ĖԊ|�����������̉e�����̖ʐ�
���ڂ����Ƃ����C�f��A�ɂƂ��Ă͍ł��s���ɂȂ�B
���������ĖԊ|�����������̉e�����̖ʐ�![]() �i�P�ʂ�m
�i�P�ʂ�m![]() �j�����߂āC
���ꂪ�ő�ɂȂ�悤�Ȉʒu
�j�����߂āC
���ꂪ�ő�ɂȂ�悤�Ȉʒu![]() �����߂��������
�����߂��������
�ƂȂ�̂ŁC������7.1m�̈ʒu����10m�̋�Ԃ�![]() ���ډׂ��C
�c��̕����S�̂�
���ډׂ��C
�c��̕����S�̂�![]() ���ڂ����Ƃ��ɁC�f��A�͍ł��h���ɂȂ邱�Ƃ��킩��B
���̂Ƃ��Ԋ|�������e�����ʐς�
���ڂ����Ƃ��ɁC�f��A�͍ł��h���ɂȂ邱�Ƃ��킩��B
���̂Ƃ��Ԋ|�������e�����ʐς�
![]() m�ł���C�Ԋ|�����Ă��Ȃ�
�����̉e�����ʐς�
m�ł���C�Ԋ|�����Ă��Ȃ�
�����̉e�����ʐς�
![]() m�ƎZ��ł���B����������
�f��A���ő�Ȃ����[�����g
��
m�ƎZ��ł���B����������
�f��A���ő�Ȃ����[�����g
��
�Ƌ��߂���B
���ɂ���f��R�ɑ���v��z�肵�悤�B�f��A�̂���f�͂�
�e����
![]() �͐}-2.50�Ɏ������ʂ�ł��邪�C
���͂���f�͂́C
�f��A�����x�_��̒f��B�̕����������ɂȂ��Ă��邱�Ƃ�
���ӂ��Ȃ���Ȃ�Ȃ��B
�����}-2.50�̍����ɒf��B�̂���f�͂�
�e����
�͐}-2.50�Ɏ������ʂ�ł��邪�C
���͂���f�͂́C
�f��A�����x�_��̒f��B�̕����������ɂȂ��Ă��邱�Ƃ�
���ӂ��Ȃ���Ȃ�Ȃ��B
�����}-2.50�̍����ɒf��B�̂���f�͂�
�e����
![]() ��`�����B
���̖ʐς̕����C���̏�̒f��A�̂���f�͂̉e�����i������
��́j�ʐς����傫���B
���������āC���E��Ԃ̂���f��R�ɂ��Đv����ꍇ�ɂ́C
�f��B�̉e������p���Ȃ���Ȃ�Ȃ��B�}�̉E���Ɏ������悤�ɁC
���̏ꍇ�͍��Ɋđ傫�߂̉d���ڂ�������B
�Ȃ���R�̏ꍇ�Ɠ��l�̉e�����ʐρi�P�ʂ�m�j�̎Z�������ƁC���ǁC
�f��B���ő傹��f��
��
��`�����B
���̖ʐς̕����C���̏�̒f��A�̂���f�͂̉e�����i������
��́j�ʐς����傫���B
���������āC���E��Ԃ̂���f��R�ɂ��Đv����ꍇ�ɂ́C
�f��B�̉e������p���Ȃ���Ȃ�Ȃ��B�}�̉E���Ɏ������悤�ɁC
���̏ꍇ�͍��Ɋđ傫�߂̉d���ڂ�������B
�Ȃ���R�̏ꍇ�Ɠ��l�̉e�����ʐρi�P�ʂ�m�j�̎Z�������ƁC���ǁC
�f��B���ő傹��f��
��
�Ƌ��߂���B
�g���X�̂Ƃ��Ɠ��l�C�Ȃ�����ꍇ�̈����苭�x�ƈ��k���x
�����ꂼ��
![]() ,
,
![]() �Ƃ���ƁC
�����葤�ƈ��k���̋Ȃ����x�͎�(2.10)����
���ꂼ��
�Ƃ���ƁC
�����葤�ƈ��k���̋Ȃ����x�͎�(2.10)����
���ꂼ��
![]() ,
,
![]() �ł���̂ŁC
���S���m�ۂ���邽�߂ɂ͏㎮(
�ł���̂ŁC
���S���m�ۂ���邽�߂ɂ͏㎮(![]() )�̍ő�Ȃ����[�����g�ɑ���
)�̍ő�Ȃ����[�����g�ɑ���
�����Ȃ���Ȃ�Ȃ��B���ꂩ��f�ʂ�
������悤�ɐv����Ȃ���Ȃ�Ȃ����ƂɂȂ�B �g���X�̏ꍇ�Ɠ��l�ޗ����x�����k�ƈ�����ňقȂ�̂͊�Ɋ������邩�� ����Ȃ����C�Ȃ�����ꍇ���ޗ��ɂ���ẮC ���邢�͏�-7�Ő�������������ۂ̂��߂ɁC ���k�ƈ�����Ƃł͋��x���قȂ�i��-7.7.3�� ��(7.92) (7.95)�Q�Ɓj���Ƃ� ����̂ŁC���̂悤��2�d�̊m�F���K�v�ɂȂ�̂ł���B
�܂������ɁC�ő傹��f�͂��x������悤�ɁC
����f���x�ɑ��Ēf�ʂ͐v����Ă��Ȃ���Ȃ�Ȃ��B
�܂����͂ŗ^�����鋖�e����f���́i����f���x
�j�́C��q�̎�(3.77)�������ɂ���
�ŗ^�����Ă���B���Ƃ͂���f�͂Ƃ���f���͂̊W�C�܂�C
�f�ʂ̒�R�W����m��K�v�����邪�C����͏��X����B
�ڍׂ͐�-4.6.1�Ő������邪�C
����f�͂̏ꍇ�͎��͂Ɠ��l�C���炩�̒f�ʐς��ߎ��I�Ȓ�R�W���ɂȂ��Ă����
�l���邱�Ƃ������B���̒f�ʐς�![]() �Ƃ���ƁC�g���X�̐v�Ɠ��l�C
����f�ɑ��Ĉ��S���m�ۂ��邽�߂ɂ́C
��(
�Ƃ���ƁC�g���X�̐v�Ɠ��l�C
����f�ɑ��Ĉ��S���m�ۂ��邽�߂ɂ́C
��(![]() )�̍ő傹��f�͂ɑ���
)�̍ő傹��f�͂ɑ���
�ɂȂ�悤�ɒf�ʐ�![]() �����肷��C���S�Ȑv���ł������ƂɂȂ�B
�Ⴆ��I�`�f�ʂ̂悤�ȏꍇ�̓E�F�u�̕��������̖ʐς�
�����肷��C���S�Ȑv���ł������ƂɂȂ�B
�Ⴆ��I�`�f�ʂ̂悤�ȏꍇ�̓E�F�u�̕��������̖ʐς�![]() �ɗp���Ă���B
�ɗp���Ă���B
���Đ�-![]() �ł́C
�����`�f�ʂ̂悤�Ȃ��̂��I�`�̂悤�Ȓf�ʂ̕����͊w�I�Ɍ��ʓI�ł����
�q�ׂ��B�����ŁC�g���X�̒f�ʐϔ��Ƃ�����R���Ƃ�
�Δ���O���ɒu���āC�����`�̂Ƃ��ƒf�ʐς͓����i�g���X�I�ȋ��x��
�����j�Ō`��I�`�ɂȂ�悤�ɂ����ꍇ�̒f�ʌW���̓��������Ă݂悤�B
�Ⴆ�ΐ}-2.51�̂悤��I�`�f�ʂ�
�f�ʐς͐}-2.49�̒����`�̒f�ʐςƓ����ł���B
�����Ő}�������悤�ɁC���������͂̍ő�l��
�ł́C
�����`�f�ʂ̂悤�Ȃ��̂��I�`�̂悤�Ȓf�ʂ̕����͊w�I�Ɍ��ʓI�ł����
�q�ׂ��B�����ŁC�g���X�̒f�ʐϔ��Ƃ�����R���Ƃ�
�Δ���O���ɒu���āC�����`�̂Ƃ��ƒf�ʐς͓����i�g���X�I�ȋ��x��
�����j�Ō`��I�`�ɂȂ�悤�ɂ����ꍇ�̒f�ʌW���̓��������Ă݂悤�B
�Ⴆ�ΐ}-2.51�̂悤��I�`�f�ʂ�
�f�ʐς͐}-2.49�̒����`�̒f�ʐςƓ����ł���B
�����Ő}�������悤�ɁC���������͂̍ő�l��
![]() �ɂȂ�����
����ƁC���͕��z��
�ɂȂ�����
����ƁC���͕��z��![]() �̈ʒu�ɂ���f�ʂ�
�̈ʒu�ɂ���f�ʂ�
�ƂȂ�̂ŁC�Ȃ����[�����g�͂��̒�`����
�ƂȂ�B![]() ��
��
![]() �ł�
�ł�![]() �C
�C
![]() �ł�
�ł�![]() �ł���B�����ϕ������
�ł���B�����ϕ������
�Ƌ��߂���B�܂�
�Ƃ����W�ɂȂ�B
��(2.11)��O���ɒu���C
��苭���Ȃ����ނ���邽�߂ɂ͒f�ʌW��![]() ��傫������������Ƃ��킩��B
���������āC�����`�̂Ƃ��̒f�ʌW����(2.10)��I�`
�f�ʂ�
��傫������������Ƃ��킩��B
���������āC�����`�̂Ƃ��̒f�ʌW����(2.10)��I�`
�f�ʂ�![]() ��
��r�����
��
��r�����
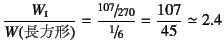 �ƂȂ邱�Ƃ���C
�����f�ʐρi�R�X�g���邢�͎��͂ɑ��鐫�\�͂قړ����j�Ȃ���C
�Ȃ��ɑ��Ă͂���I�`�f�ʂ̕���2.4�{�����\���ɂȂ��Ă��邱�Ƃ��킩��B
�Ȃ��C�����ł�
�ƂȂ邱�Ƃ���C
�����f�ʐρi�R�X�g���邢�͎��͂ɑ��鐫�\�͂قړ����j�Ȃ���C
�Ȃ��ɑ��Ă͂���I�`�f�ʂ̕���2.4�{�����\���ɂȂ��Ă��邱�Ƃ��킩��B
�Ȃ��C�����ł�![]() ,
, ![]() ��2���ɑ��đΏ̂Ȓf�ʌ`��̏ꍇ�Ɍ��肵��
�f�ʌW���̒�`��p���Ă��邱�Ƃɂ͒��ӂ��ė~�����B
�C�ӂ̒f�ʌ`�̏ꍇ�͏�-4�Ő������闝�����Q�Ƃ��ė~�����B
��2���ɑ��đΏ̂Ȓf�ʌ`��̏ꍇ�Ɍ��肵��
�f�ʌW���̒�`��p���Ă��邱�Ƃɂ͒��ӂ��ė~�����B
�C�ӂ̒f�ʌ`�̏ꍇ�͏�-4�Ő������闝�����Q�Ƃ��ė~�����B
���̓�̒f�ʗ͂�
����f�͂ƋȂ����[�����g�͏ꏊ![]() �̊��ɂȂ邱�Ƃ��킩�����Ǝv���B
�����̉Ȋw���ۂ͂����̐������f���Œ莮������C���ꂪ�\����v��
�p�����邪�C�قƂ�ǂ̏ꍇ����͔����������ŕ\�����B
�܂�C����f�͂ƋȂ����[�����g�Ƃ����m�肽���E�\�����������́C
�͊w�����Ƃ��Ă��������������������̂Ƃ��ă��f���������B
�O�߂܂łɗp���Ă����荇�������́C
����f�ʂɐ��������͂ƊO�͂́u�����I�ȁv�荇���ł��������C
�����ł́u�Ǐ��I�ȁv�C�܂蕨�̒��̂���_
�̊��ɂȂ邱�Ƃ��킩�����Ǝv���B
�����̉Ȋw���ۂ͂����̐������f���Œ莮������C���ꂪ�\����v��
�p�����邪�C�قƂ�ǂ̏ꍇ����͔����������ŕ\�����B
�܂�C����f�͂ƋȂ����[�����g�Ƃ����m�肽���E�\�����������́C
�͊w�����Ƃ��Ă��������������������̂Ƃ��ă��f���������B
�O�߂܂łɗp���Ă����荇�������́C
����f�ʂɐ��������͂ƊO�͂́u�����I�ȁv�荇���ł��������C
�����ł́u�Ǐ��I�ȁv�C�܂蕨�̒��̂���_![]() �ߖT��
���ڂ����Ƃ��̂荇���������l���C
���̍l�@��������������ŕ\���ꂽ�荇���������߂Ă������B
�\���͊w�����߂Ċw�Ԑl�̍ŏ��̓�ւ��e�������B
���ɋȂ����[�����g�C�����Ă��̎��������������Ŗ��������Ƃ����Ƃ��낾�낤�B
���Ɂu�����������������v�Ƃ����s�ׂ��̂��̂ƁC
�u���E���������̐�����傫�����E����v�Ƃ������Ƃ�
�Ȃ��Ȃ�����邱�Ƃ��ł����C
���܂������ɂȂ��ւ̈�ł�����B
�������Ă��邩�����ł���i�o����̂ł͂Ȃ��j�܂ŁC���x�����K�����ė~�����B
�ߖT��
���ڂ����Ƃ��̂荇���������l���C
���̍l�@��������������ŕ\���ꂽ�荇���������߂Ă������B
�\���͊w�����߂Ċw�Ԑl�̍ŏ��̓�ւ��e�������B
���ɋȂ����[�����g�C�����Ă��̎��������������Ŗ��������Ƃ����Ƃ��낾�낤�B
���Ɂu�����������������v�Ƃ����s�ׂ��̂��̂ƁC
�u���E���������̐�����傫�����E����v�Ƃ������Ƃ�
�Ȃ��Ȃ�����邱�Ƃ��ł����C
���܂������ɂȂ��ւ̈�ł�����B
�������Ă��邩�����ł���i�o����̂ł͂Ȃ��j�܂ŁC���x�����K�����ė~�����B
�}-2.52�ɂ́C�P�ʒ���������̔C�ӂ̊���
�^����ꂽ���z�d![]() ����p���Ă��钷��
����p���Ă��钷��![]() �̗���`�����B
���[�͂���ʉ����āC�ǂ���ɂ��O�͂���p���Ă���悤�ɏ����Ă��邪�C
�����[�����x�����Ă���ꍇ�ɂ́C�����ɂ���O�͔͂��͂Ɖ��߂��ė~�����B
�O�͂̌����͐}-2.33�̒�`�ɏ]�����B
�܂��荇���������߂邽�߂ɁC���̑ȉ~�̒��ɕ`�����悤�ȁC
�C�ӂ̓_
�̗���`�����B
���[�͂���ʉ����āC�ǂ���ɂ��O�͂���p���Ă���悤�ɏ����Ă��邪�C
�����[�����x�����Ă���ꍇ�ɂ́C�����ɂ���O�͔͂��͂Ɖ��߂��ė~�����B
�O�͂̌����͐}-2.33�̒�`�ɏ]�����B
�܂��荇���������߂邽�߂ɁC���̑ȉ~�̒��ɕ`�����悤�ȁC
�C�ӂ̓_![]() ����
����![]() �̒����Ŏ��o���������v�f�̂荇�����l���Ă݂�B
�܂�
�̒����Ŏ��o���������v�f�̂荇�����l���Ă݂�B
�܂�![]() �����̗͂̂荇����
�����̗͂̂荇����
�ɂȂ�B���̎�������ƁC����![]() �����̂荇������
�����̂荇������
�Ƃ��������������ŕ\�����B���ɂ���![]() �̉E�[�𒆐S�ɂ���
�����v���̃��[�����g�̂荇�����Ƃ��
�̉E�[�𒆐S�ɂ���
�����v���̃��[�����g�̂荇�����Ƃ��
�̂悤�ɂȂ�B���z�d�ɂ�郂�[�����g�́C![]() �����������ł��邱�Ƃ���C
���v
�����������ł��邱�Ƃ���C
���v![]() �̗͂�
�̗͂�![]() �̒����ɍ�p���Ă���Ƒ����ĎZ�肵�Ă���B
���̎�����������
�̒����ɍ�p���Ă���Ƒ����ĎZ�肵�Ă���B
���̎�����������![]() ��1���̍��i�ŏd�v���j������
���o���ƁC���ǃ��[�����g�̂荇������
��1���̍��i�ŏd�v���j������
���o���ƁC���ǃ��[�����g�̂荇������
�Ƃ��������������ŕ\�����B���̎��͂ǂ����Ō������Ƃ͂Ȃ����낤���B
�����C���Ɏ�(2.9)�Ŏ��������̂Ɠ����ŁC
���[�����g�}�̌��z������f�͐}�ɂȂ�Ƃ������Ƃ������Ă���B
�ŏI�I�ɁC��(2.13)�Ǝ�(2.14)����![]() ��
��������C���̒f��
��
��������C���̒f��![]() �ɂ�����荇����\���Ǐ��I�Ȕ�����������
�ɂ�����荇����\���Ǐ��I�Ȕ�����������
(2.15)
�ƕ\�����Ƃ��ł���B
���Ĕ����������������Ƃ��C�ϕ�����x�ɐϕ��萔�Ƃ�������萔����������B
���̒萔��K�Ɍ���ł��Ȃ��ƁC���͗B��ɋ��߂�ꂽ���Ƃɂ͂Ȃ�Ȃ��B
���̏ꍇ�ɂ́C�[���̏����̒萔�����肷��B
���̂悤�ȏ�^����������C���E�����ƌĂ�ł���B
�܂�![]() �ł̋��E���������߂邽�߂ɁC�}-2.52��
���̑ȉ~�̒������ė~�����B����́C�����`�f�ʂ̗��Ƃ��āC
�[���𔖂���o�������̂ł���B��O�̌����Ă���ʂ͓����̒f�ʂȂ̂ŁC
�����ɂ͓�̒f�ʗ͂𐳂��������ō�p�����Ă���B
���������̖ʂ͊O���̖ʂŁC�O�͂���p���Ă���ʂł���B
���E�����́C���̔��������̂荇�����狁�߂���B
�܂�C
�ł̋��E���������߂邽�߂ɁC�}-2.52��
���̑ȉ~�̒������ė~�����B����́C�����`�f�ʂ̗��Ƃ��āC
�[���𔖂���o�������̂ł���B��O�̌����Ă���ʂ͓����̒f�ʂȂ̂ŁC
�����ɂ͓�̒f�ʗ͂𐳂��������ō�p�����Ă���B
���������̖ʂ͊O���̖ʂŁC�O�͂���p���Ă���ʂł���B
���E�����́C���̔��������̂荇�����狁�߂���B
�܂�C![]() �����̗͂̂荇���ƁC���[�����g�̂荇������
�����̗͂̂荇���ƁC���[�����g�̂荇������
���C���[�ł̋��E�����ɂȂ�B
���l�ɁC�}-2.52�̉E���̑ȉ~�ɕ`��������C![]() �ł�
���E���������߂悤�B�����ł�I�`�f�ʂ���������z�肵���}�ɂȂ��Ă���B
�����ł��͂ƃ��[�����g�̂荇������
�ł�
���E���������߂悤�B�����ł�I�`�f�ʂ���������z�肵���}�ɂȂ��Ă���B
�����ł��͂ƃ��[�����g�̂荇������
���C�E�[�ł̋��E�����ɂȂ�B
���ɁC���̒��ԕ��ɏW������f�͂�W���O�̓��[�����g����p���Ă���
�ꍇ�̏������l���Ă݂悤�B
�����͒[���ł͂Ȃ����Ƃ���C�A�������ƌĂ�邱�Ƃ�
�����B�}-2.53�Ɏ������̂́C![]() ��
�W���d����p���Ă���ł���B
���E�����̏ꍇ�Ɠ��l�C���̍ډד_������Ŕ����f�ʂ��o���C
���̂荇�����l����B
�ډד_�̑O�����ʂ��邽�߂ɁC�L��
��
�W���d����p���Ă���ł���B
���E�����̏ꍇ�Ɠ��l�C���̍ډד_������Ŕ����f�ʂ��o���C
���̂荇�����l����B
�ډד_�̑O�����ʂ��邽�߂ɁC�L��
![]() ��t������B
���̔��Ђ̗͂ƃ��[�����g�̂荇�����Ƃ��
��t������B
���̔��Ђ̗͂ƃ��[�����g�̂荇�����Ƃ��
�ƂȂ�B��(2.14)����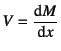 �Ȃ̂ŁC�ŏI�I�ȘA��������
�Ȃ̂ŁC�ŏI�I�ȘA��������
�Ƌ��߂���B
�O�߂ŋ��߂��悤�ɁC�Ò���̖��́C�[���̋��E�����ƁC
���̏ꏊ�ꏊ�ł̔����������Ő����I�ɂ̓��f��������Ă���B
���̂悤�ɋL�q���ꂽ�������E�l���
�ƌĂ�ł���B���̖��̉������̗�Ƃ��āC�}-2.34��
�����������z�d����p�����Ў������������Ă݂悤�B
�܂��荇�����Ƌ��E�����́C��(2.15a) (2.17)����
�ƕ\�����B���[�͊O�͂��^�����Ă��Ȃ����狫�E�����ɂ�
�Ȃ�Ȃ��B
![]() ������C���̔����������̈�ʉ���
������C���̔����������̈�ʉ���
�ɂȂ�̂ŁC��(2.15b)�̂���f�͂ƋȂ����[�����g��
�W���l�����āC���E�����ɑ�������
�ƂȂ�B����������![]() ,
,
![]() �ƌ���ł���B
��������
�ƌ���ł���B
��������![]() �̕\���ɑ�����邱�Ƃɂ����
�̕\���ɑ�����邱�Ƃɂ����
�Ƌ��߂���B�����p.![]() �̎�(
�̎�(![]() )�ƈ�v����B
���߂�ꂽ���ʂ�
)�ƈ�v����B
���߂�ꂽ���ʂ�![]() �̋��E������(2.16)�ɑ�������
�̋��E������(2.16)�ɑ�������
�ƂȂ�C���[�̔��͂����������߂��Ă���B
������̗�Ƃ��āCsine���ŗ^����ꂽ
���z�d
![]() ��
��p���Ă���P�����������Ă݂悤�B�荇�����Ƌ��E������
��
��p���Ă���P�����������Ă݂悤�B�荇�����Ƌ��E������
�ƕ\�����B![]() �͕��z�d�̍ő�l�ł���B
���E�����́C���[���s���x���Ŏx�����Ă��邱�Ƃ���C
�Ȃ����[�����g�����[�ŗ�Ƃ������̂ɂȂ�B
���̏ꍇ�̈�ʉ���
�͕��z�d�̍ő�l�ł���B
���E�����́C���[���s���x���Ŏx�����Ă��邱�Ƃ���C
�Ȃ����[�����g�����[�ŗ�Ƃ������̂ɂȂ�B
���̏ꍇ�̈�ʉ���
�ɂȂ�̂ŁC���E�����ɑ�������
�ƂȂ�̂ŁC![]() ,
, ![]() �Ƌ��߂���B���������ċȂ����[�����g���z��
�Ƌ��߂���B���������ċȂ����[�����g���z��
�ƂȂ�B����f�͕��z�͂����![]() �Ŕ���������߂��C
���[�̎x�_���͂͂���𗼒[�̂���f�͂̋��E�����ɑ������
�Ŕ���������߂��C
���[�̎x�_���͂͂���𗼒[�̂���f�͂̋��E�����ɑ������
�Ƌ��߂���B�O�͂̑��a��
![]() �ł��邩��C
������̗͂Ƃ��Đ��������͂����߂��Ă���B
�ł��邩��C
������̗͂Ƃ��Đ��������͂����߂��Ă���B
�Ō�ɁC�X�p���̎O���̈�̈ʒu�ɏW���d����p����
�P�����ip.![]() �̐}-2.36�j�������Ă݂悤�B
���̏ꍇ�́C
�̐}-2.36�j�������Ă݂悤�B
���̏ꍇ�́C
![]() ,
,
![]() ��
����Ԃł̂荇������
��
����Ԃł̂荇������
![$\D*[2]{M}{x}=0$](s1img441.gif) ������C��ʉ��͗���ԋ���
������C��ʉ��͗���ԋ���
�ł���B���E������
�ł���C�A�������͎�(2.18)����
![]() �Ƃ���
�Ƃ���
�ƕ\�����B�ȏ��4�������Ɉ�ʉ��������Đ��������
�ƂȂ�̂ŁC![]() �𑼂̎��ɑ�������
�𑼂̎��ɑ�������
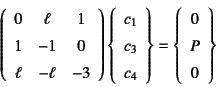
�̘A���������������������ƂɂȂ�C����
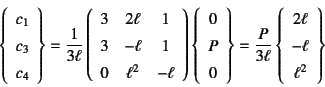
�ƂȂ�̂ŁC�Ȃ����[�����g���z��
�Ƌ��߂���B
�����p.![]() ��
��(
��
��(![]() )��p.
)��p.![]() �̎�(
�̎�(![]() )�ƈ�v����B
)�ƈ�v����B