最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。

• 7.7.1 ねじれ座屈
• 7.7.2 横倒れ座屈
• 7.7.3 曲げ引張り・圧縮強度

7.7 曲げねじりと安定問題

7.7.1 ねじれ座屈

ねじりの自由度も持ち立体的に挙動する棒も，章-6で 取り上げた基本的な分岐座屈の一つである 曲げ座屈と同じ様な分岐現象を示すことがある。 ここでは代表的な二つを紹介するが，基礎式の誘導や解法については 別途参考文献[125,126]等を参照のこと。

図 7.38: 柱のねじれ座屈

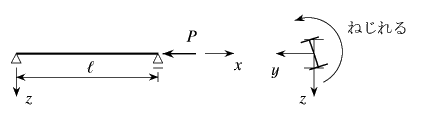
最初の例は図-7.38に示したような系の分岐現象で， 柱の曲げ座屈に非常に似ている。つまり，例えば図示したような 単純支持された棒を圧縮した場合に，ある外力レベルまでは 棒は単に縮むだけである。 これがある外力レベルになったとき，それまでの単に 縮むだけの変形特性とは全く異なるねじれ変形を発生させる ことがある。これを柱のねじれ座屈 と呼んでいる。 図のような境界条件の場合の座屈荷重は

$$P_\varphi\equiv \dfrac{1}{r_p^2}\left( GJ+\dfrac{\pi^2EI_\omega}{\ell^2} \right)$$ (7.89)

と求められている。ここに$r_p$は断面の極2次モーメント に関する回転半径であり

$$r_p\equiv\sqrt{\dfrac{I_p}{A}}, \quad I_p\equiv\int_A \left\{(y-y_s)^2+(z-z_s)^2\right\}\dint A$$ (7.90)

で定義されている。ただし，自己展開型宇宙構造系のように非常に剛性が 低いものを除き，通常の鋼薄肉構造断面では， この$P_\varphi$が系の強度を支配するようなことは稀である。 このような座屈が生じる原因は，ねじり変形を許容した場合に断面に そりが発生して断面が平面でなくなり，軸線方向以外の方向への 軸力の成分が生じることにある。ただ，このそり変形が非常に小さい ため，上記のように通常の断面形状の鋼構造物でこの座屈が問題に なることはない。

7.7.2 横倒れ座屈

図 7.39: 梁の横倒れ座屈

もう一つの例は，図-7.39にあるような分岐座屈である。 単純梁に等曲げを作用させた場合には，$x$-$z$面内で曲げ変形が 生じるが，この外力モーメントがあるレベルに達した ときに断面が面外に倒れてしまう 現象が起こる。これを梁の横倒れ座屈 あるいは横ねじれ座屈 と呼ぶ^7.5が， やはりある外力レベルまでの曲げ変形とは大きく異なる， 曲げねじりを伴う変形に突然移行する。分岐座屈の代表的な 例の一つである。 この場合の座屈荷重は

$$(C_0)_\omega\equiv \sqrt{ \dfrac{\pi^2EI_y}{\ell^2} \left(GJ+\dfrac{\pi^2EI_\omega}{\ell^2}\right)}$$ (7.91)

と求められている。 ここに$I_y$は式(7.78d)で定義された 断面の弱軸（$z$軸）回りの断面2次モーメントである。 この横倒れ座屈は，次の節で説明するように， 鋼構造物の設計に当たっては必ず検証すべき 重要な要件の一つになっている。 軸力が同時に作用しているような場合の座屈荷重等については 別途参考文献[126]等を参照のこと。

7.7.3 曲げ引張り・圧縮強度

図 7.40: 示方書で規定されている圧縮強度

曲げを受ける部材の引張り側は，材料そのものの強度まで耐えられるから， 許容応力設計法の考え方では 降伏応力を用いて曲げ引張り許容応力 $\sigma_a^{(bt)}$（曲げ引張り強度 ）を

$$\sigma_a^{(bt)}=\dfrac{\sigma\sub{cr}^{(bt)}}{\gamma},\qquad \sigma\sub{cr}^{(bt)}\equiv\sigma\subsc{y}$$ (7.92)

で与えていい。ここに$\gamma$は安全率 である。 これに対し，曲げを受けた部材の圧縮側の強度は， 前節の横倒れ座屈で支配されることがある。 つまり，例えば2主桁を複数の対傾構でつないだ場合， その対傾構間隔を座屈長$\ell$とする横倒れ座屈の可能性が生じる。 したがって，そうならないように材料そのものの強度とは異なる強度として， 曲げ圧縮許容応力 $\sigma_a^{(bc)}$（曲げ圧縮強度 ）を規定しなければならないと考えられている。 例えば図-7.23にあるI形断面の 場合には，Saint-Venantのねじり定数が比較的小さいことから， 式(7.91)の座屈モーメントから 算定できる座屈応力を

$$\dfrac{\sigma\sub{cr}^{(bc)}}{\sigma\subsc{y}}=\dfrac{1}{\lambda_b^2}$$ (7.93)

のように近似できる[123]。 ここに $\sigma\subsc{y}$は降伏応力であり，$\lambda_b$は 横倒れ座屈に関する細長比パラメータ で

$$\lambda_b\equiv \dfrac{2 K}{\pi} \sqrt{\dfrac{\sigma\subsc... ...\dfrac{A\subsc{w}}{2A\subsc{f}}} \index{=lambdab@$\lambda_b$}%$$ (7.94)

で定義されている。 ここに$b$はフランジ幅であり，$A\subsc{w}$と$A\subsc{f}$はウェブと フランジの断面積である。この座屈応力と細長比パラメータの関係は， 形式的にはEuler荷重のそれと同じである。 この理論値に対して，実際の曲げ圧縮許容応力は

$$\sigma_a^{(bc)}=\dfrac{\sigma\sub{cr}^{(bc)}}{\gamma}, \qqua... ...a_b-0.2\right) & 0.2 < \lambda_b < \sqrt{2} \end{array}\right.$$ (7.95)

のように規定[128]されている。図-7.40に その関数を，Euler曲線と比較して描いた。

最新版を正確に読むためには pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。