最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。

• 7.4.1 I形断面棒の曲げねじり
  • 7.4.1.1 断面のそり
  • 7.4.1.2 フランジの曲げ変形
  • 7.4.1.3 曲げねじりモーメント
  • 7.4.1.4 曲げねじりのつり合い式と境界条件
  • 7.4.1.5 応力分布
  • 7.4.1.6 直応力分布とねじり抵抗
  • 7.4.1.7 そり関数とねじりによる直応力分布
  
  
• 7.4.2 曲げねじりの境界値問題
  • 7.4.2.1 片持ち棒のねじり
  • 7.4.2.2 曲げねじりとSaint-Venantのねじりの比較
  • 7.4.2.3 単純支持点での境界条件
  
  
• 7.4.3 一般化した曲げねじり理論における断面座標・定数と応力分布

7.4 薄肉断面棒の曲げねじり

7.4.1 I形断面棒の曲げねじり

7.4.1.1 断面のそり

図 7.22: I形断面棒とスリット入り円管の断面のそり

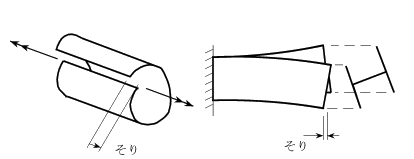
前節最後の例にあるスリットの入った円管のねじりを， 丸めた紙で実演してみよう。図-7.22の左側にも 描いたように（はならず，本当は紙が重なってしまうが，微小な 変形の範囲なら図のように）断面にそり が発生する。つまり，ねじったあとの断面がその平面を保持できなくなる。 この「そり」は，例えば前節の長方形断面の場合の$x$方向変位成分 式(7.22)の第2項である。 この「そり」がI形断面棒をねじったときにも発生するだろうと いうことは，容易に予想できる。同じく図-7.22の右に その様子を誇張して示しておいた。

ではスリットの入った円管棒のどちらかの端部が壁に固定されていたり， ダイアフラムが入っていて断面が平面を保持するように拘束されている 場合を考えよう。こうすると，図-7.22左側のような そりを拘束してしまい， その反作用として軸方向の直応力$\sigma_{xx}$が 生じてしまうことも，容易に想像できないだろうか。そうなると， この直応力が間接的にねじり外力に抵抗するのではないだろうか。 前節までは直応力もそりも無視してきたが， 薄肉断面棒で特に開断面の場合には，この二つを無視できない ような気がする。 一般論についてはこれも別途参考書[125]等を参照して 欲しいが，その力学的特性をI形断面棒に限定して概説する。

7.4.1.2 フランジの曲げ変形

図-7.22の右図には，ねじりを受けた片端固定のI形 断面棒を上フランジ側から見た状況を示してある。 このフランジだけに注目すると， フランジはその面内で曲げを受けて片持ち梁として変形している ようには見えないだろうか。そして，この曲げによって発生した軸方向の 変位成分が，断面のそり変位成分になっているように見える。 一方ウェブの方は，前節の薄肉長方形断面とみなすことができ，せいぜい 式(7.22)右辺第2項程度のそり成分しかなく， 無視できるほど小さいと考えていいだろう。 そこで，このフランジの曲げによる抵抗力が，ねじりに 対してどのような抵抗を示すのか検討しておこう。

図 7.23: I形断面のねじり変形
図 7.24: 上フランジに発生する曲げ応力成分の分布

図-7.23には断面寸法と，ねじられて回転した 状態の断面図とを描いてある。上フランジだけを上から見る限り， 片持ち梁が$x$-$y$面内で$y$方向に 曲げを受けている状態として捉えることができる。 この曲げによるフランジ中心線の$y$方向の変位が

$$v(x)=\dfrac{h}{2} \varphi(x)$$ (7.29)

の大きさになっているのは，図-7.23からも 明らかである。 もちろん原点回りにねじり回転もしているが， その抵抗は前節の薄肉長方形断面のねじり抵抗として 既に考慮済みである。ここではそれ以外に， 上述のようにフランジが曲げを受けることによってフランジ内に生じる 直応力やせん断応力がねじり抵抗になっている可能性を示唆している。 その分布は図-4.68に示した通りで あり，図-7.24にも示しておいた。 このせん断応力に着目すると， それは曲げによって発生するせん断力という断面力を発生させ， 次の図-7.25のようなせん断力$V_f$が生じている。 上下のフランジが，$y$方向に向かってそれぞれ反対方向に曲げを 受けているため，同図の右側にあるように， 上フランジには$y$の正の方向に， 下フランジにはその負の方向に同じ大きさのせん断力$V_f$が 生じている。この二つのフランジ内のせん断力$V_f$が 逆向きであることから，それは$x$軸回りの 偶力$(h\times V_f)$を発生させ， それがねじり外力に対する抵抗力になるのは明らかではないだろうか。 これが曲げによってねじりに抵抗している部分なのだ。

図 7.25: フランジに発生するせん断力とそれが作るねじり抵抗

まず$V_f$を算定しておこう。図-7.23の右図に戻って， 上フランジの$y$方向の 横変位を $v(x)\equiv\left(\slfrac{h}{2}\right)\varphi(x)$と すると，初等梁理論式(4.5a)より， これに伴う$x$方向変位つまりそり変位 は

$$u(x,y)=-y v'(x)$$ (7.30)

になる。したがって，これによって発生する伸びひずみと直応力は

(7.31)

となり，結局フランジの曲げにより発生する曲げモーメントは

$$M_f(x)\equiv\int_{A_f} y \sigma_{xx}\dint A=-EI_f v''(x)$$ (7.32)

と算定できる。ここに$A_f$は上フランジ断面積であり

$$I_f\equiv \int_{A_f} y^2\dint A = \dfrac{t_f b^3}{12}$$

は上フランジ断面の$z$軸回りの断面2次モーメントである。 さらに曲げによるせん断力は，図-7.25の左図の つり合いを考えるまでもなく

$$V_f(x)=M_f'(x)=-EI_f v'''(x) \eqno{(a)}$$

であることは，初等梁理論から明らかである。梁の曲げ理論の範囲内での せん断応力分布は式(4.79)で得ており， 上フランジでは

$$\sigma_{xy}(x,y)=-\dfrac{V_f(x) G_y(y)}{t_f I_f}, \quad ... ...slfrac{-b}{2}}^y \xi t_f(\xi) \dint \xi \index{=gy@$G_y$}%$$ (7.33)

となっている。$\xi$は$y$に関する積分のための補助変数である。

7.4.1.3 曲げねじりモーメント

図-7.25の右図にあるように，上下フランジには 同じ大きさで逆向きのせん断力$V_f$が発生しており， この力が作る抵抗力としての偶力が，ねじり外力に 抵抗する成分になっているから，式($a$)を 用いてその偶力は

$$T_\omega(x) \equiv h\times V_f(x) = h \times\left\{ -EI_f v'''(x) \right\} \eqno{(b)}$$

となる。式(7.29)を上式($b$)の最右辺に 代入すると

$$T_\omega(x) = -E\left(I_f \dfrac{h^2}{2} \right) \varphi'''(x)$$

となるので，右辺の括弧内を新たに

$$I_\omega\equiv I_f \dfrac{h^2}{2}=\dfrac{1}{24} t_f b^3 h^2$$ (7.34)

と定義してしまえば，フランジが曲げを受けることによって ねじりに抵抗する成分は

$$T_\omega(x)=-EI_\omega \varphi'''(x)$$ (7.35)

と書くことができる。ここに，$I_\omega$はそり2次モーメント と呼ばれ， $[\mbox{長さ}]^6$の次元を持つ。

ここで便宜上，式($a$)の両辺に$h$を乗じた関係式から， 式($b$)の$T_\omega$に 対応する新たな断面力として

$$T_\omega(x)=M_\omega'(x), \quad \mbox{つまり} \quad M_\omega(x)\equiv h\times M_f(x)$$ (7.36)

になるような$M_\omega(x)$を定義しておく。 これは曲げねじりモーメント と呼ばれる断面力である。式(7.35)に対応させれば

$$M_\omega(x)=-EI_\omega \varphi''(x) \index{=momega@$M_\omega$}%$$ (7.37)

という関係を持ち，$EI_\omega$は曲げねじり剛性 と呼ばれる。

式(7.33)に式($a$)を代入したあと， 式(7.29)の$v(x)$と$\varphi(x)$の関係を代入すれば， 発生するせん断応力も上フランジで

$$\sigma_{xy}(x,y)=\dfrac{E}{t_f} \left\{ \int_{\slfrac{-b}{2... ...left(\xi \dfrac{h}{2}\right) \dint \xi \right\} \varphi'''(x)$$

と表現できる。この式と式(7.35)から$\varphi$を 消去すると，最終的に

$$\sigma_{xy}(x,y)=-\dfrac{1}{t_f} \overline{Q}_\omega(y) \dfrac{T_\omega(x)}{I_\omega}$$ (7.38)

となる。ここに $\overline{Q}_\omega$はそりに関する 断面1次関数で あり，上フランジで

$$\overline{Q}_\omega(y)\equiv \int_{\slfrac{-b}{2}}^y t_f(\x... ...2}\right)\dint \xi \index{=qbaromega@$\overline{Q}_\omega$}%$$ (7.39)

と定義した。$\xi$は$y$に関する積分のための補助変数である。

7.4.1.4 曲げねじりのつり合い式と境界条件

以上から薄肉棒部材のねじりに対しては， 前節までのSaint-Venantのねじり抵抗と 曲げねじり抵抗との2成分の和で抵抗することがわかった。 したがって式(7.5)のSaint-Venantのねじりモーメント$T_S$に 式($b$)の曲げねじり抵抗モーメント$T_\omega$を加えて

$$\left\{T_S(x)+T_\omega(x)\right\}'=0$$ (7.40)

がつり合い式 になる。

境界条件には，単純なねじりに関するものに加えて， 曲げねじり抵抗の成分と， いわゆるそりに関する境界条件とが必要になる。 それを誘導するために，図-7.24の上フランジの 曲げの問題に戻ろう。 式(4.23)で示したように，この梁の曲げに関する境界条件は

$$\begin{eqnarray*} v=\mbox{与えられる}\quad&\mbox{あるいは}&\quad n_i V_f=(S_f)... ...v'=\mbox{与えられる}\quad&\mbox{あるいは}&\quad n_i M_f=(C_f)_i \end{eqnarray*}$$

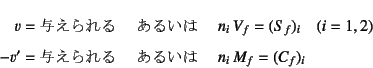
となっていた。ただこの場合の$-v'$と$C_f$はいずれも，$z$軸の 左回り方向を正とするたわみ角およびねじり外力である。 まず力の境界条件については，下フランジからの関与分も加えるために， 式($b$) (7.36)のように$V_f$と$M_f$に$h$を 乗じて偶力の形にすると，少なくとも 前者はSaint-Venantのねじりモーメントと整合した物理量になる。 さらにたわみ$v$は，式(7.29)のように$\varphi(x)$で 表されていたから，$v$を与える境界条件は$\varphi$を 与える条件になり，$v'$を与える条件は$\varphi'$を与える 条件になる。以上のことを考慮してすると，上式は

(7.41)

と書き換えてもいいだろう。

式($b$)から明らかなように，$(h\times V_f)$は ねじり力に抵抗する曲げねじりに関する成分$T_\omega$であるから， まず1行目の境界条件式(7.41a)は，式(7.7)の 力の境界条件に加えるべき $T_\omega=h\times V_f$の寄与分と 考えればよく，Saint-Venantのねじりモーメントに加えて

$$\varphi=\mbox{与えられる}\quad\mbox{あるいは}\quad n_i \left(T_S+T_\omega\right)=(C_x)_i \eqno{(c)}$$

が，曲げねじりを含んだねじり外力に関する境界条件になる。 式(7.41b)の$-\varphi'$に関する幾何学的境界条件は， 式(7.30)からも明らかなように，境界でそり変形を 与えるか否かの条件になる。また対応する力の境界条件は， 式(7.36)の$M_\omega$の定義$h\times M_f$からわかるように， 端部での$M_\omega$に相当する 曲げねじり外力モーメント成分である$h\times C_f$を 与えるか否かの，新しい条件になっている。 したがって，上の式($c$)と合わせて書き直すと，曲げねじりの境界条件 は

(7.42)

となる。ここに$C_\omega$は端部に作用させる曲げねじり外力モーメント として定義したが，次元も $[\mbox{力}][\mbox{長さ}]^2$となることから その物理的意味はあまり明解ではないが，それについては後述する。

7.4.1.5 応力分布

断面内に発生する直応力は フランジの曲げによるものが主なので，例えば上フランジでは， 式(7.31b)に式(7.29)を 代入したあと式(7.37)の関係を用いれば

$$\sigma_{xx}(x,y,z)=y \dfrac{h}{2} \dfrac{M_\omega}{I_\omega}$$ (7.43)

となる。せん断応力分布は，Saint-Venantのせん断応力成分に フランジの曲げによるせん断応力成分を加え， 上フランジでは

$$\sigma_{sx}(x,y,z)=\dfrac{T_S(x)}{J} \Theta(y,z)- \dfrac{1}{t_f} \overline{Q}_\omega(y) \dfrac{T_\omega(x)}{I_\omega}$$ (7.44)

と表現される。 なお，下フランジでは両式(7.43) (7.44)の 符号が異なるだけである。

7.4.1.6 直応力分布とねじり抵抗

図 7.26: 曲げねじり力の直感的理解のための直応力分布の概略

実際に境界値問題の例題を解く前に， 曲げねじりモーメント$M_\omega$および 対応する曲げねじり外力モーメント$C_\omega$の 物理的な意味について少し考察しておこう。 この曲げねじりモーメントを発生させている力は，上下フランジの せん断力であった。このせん断力は，上下フランジそれぞれが 曲げを受けて直応力分布が発生し，それにつり合うように生じていた。 その直応力分布の仕方を描いたのが図-7.26である。 例えば式(7.31b)は上フランジの直応力分布だが， 式(7.29)を代入すると次式のようになり， 下フランジではその符号が異なるため

$$\mbox{上フランジ:} \quad \sigma_{xx}=-E y \dfrac{h}{2} \v... ...x{下フランジ:} \quad \sigma_{xx}=E y \dfrac{h}{2} \varphi''$$

であり，上と下とで向きは逆だが$y$方向に同じような線形分布をしている。 すなわち直応力の分布は図-7.26の右端の図のように， 上フランジについては左突出端が 圧縮で右突出端が引張りに，下フランジについてはその逆の 符号の直応力分布になっている。 この応力分布はたいへん興味深い分布になっている。 つまり，同じ図-7.26の 左に模式的に示した曲げと軸力を受ける棒の基本的な三つの合応力の，2軸 回りの曲げモーメントおよび軸力のいずれをも生じさせない。これが， 断面のそりに関連して内部に発生する曲げねじりモーメント と呼ばれる抵抗力の正体である。また， 式(7.42b)の右辺の曲げねじり外力モーメント$C_\omega$も， まさにこの右端の図のような外力の作用をモデル化したものと 考えればいい。

7.4.1.7 そり関数とねじりによる直応力分布

ここまでは，I形断面の曲げねじりを，フランジの曲げと解釈して わかり易く定式化したが， 一般の薄肉断面棒も同じような曲げねじり成分を有している。 具体的な一般理論については 参考書[125]等を参照して欲しいが， 前節のI形断面の結果を，もう少し一般的な表現にしておく。まず新たに

$$\omega^*(y,z)\equiv \left\{ \begin{array}{ll} +\left(\dfr... ...}{2}\right) y & \mbox{　下フランジで} \end{array} \right.$$ (7.45)

という新しい断面座標$\omega^*(y,z)$ を導入する。 座標と呼んだが $[\mbox{長さ}]^2$の次元を有している。 これを用いると式(7.34) (7.39)の断面量は

$$I_\omega\equiv \int_A{\omega^*}^2(y,z)\dint A,\quad \overl... ...z(\xi)\right) \omega^*\left(y(\xi),z(\xi)\right) \dint \xi$$ (7.46)

と定義できる。 ここでは，元々の式(7.39)の $\overline{Q}_\omega(y)$の定義を， 肉厚中心線に沿った$s$軸に沿った積分で形式的に置き換えて一般化 してある。$\xi$は$s$に関する積分のための補助変数である。 その例については参考文献等を参照のこと。 ちなみに図-7.23の寸法のI形断面のそり2次 モーメントは $\left(\slfrac{1}{24} b^3 h^2 t_f\right)$になる。 同様にねじりによるそり変位成分も

$$u_x(x,y,z)=-\omega^*(y,z) \varphi'(x)$$ (7.47)

と書き表すことができる。$\omega^*(y,z)$はねじり率$\varphi'(x)$が単位量の ときのそり変位の断面内分布を示しているから，単位そり関数 とも呼ばれる。図-7.27に$\omega^*$と $\overline{Q}_\omega$の 分布図を描いたが，それぞれそり変位とフランジの曲げによる せん断応力分布のパターンとに一致している。

図 7.27: I形断面の単位そり関数とそりに関する断面1次関数

さらに式(7.36)の$M_\omega$の定義に 式(7.32)を代入すると

$$M_\omega\equiv\int_{A(\mbox{\scriptsize 上フランジ})} h\times y \sigma_{xx}\dint A$$

となっていた。一方， 式(7.29)と式(7.31b)から上フランジの直応力が

$$\sigma_{xx}=-E \dfrac{h}{2} y \varphi''(x)$$

であるのに対して，下フランジでは符号が逆になるだけなので， 上式はさらに

$$\begin{eqnarray*} M_\omega &=& \int_{A(\mbox{\scriptsize 上フランジ})} h y\lef... ...frac{h}{2} y\right) \left(E\dfrac{h}{2}y\varphi''\right)\dint A \end{eqnarray*}$$

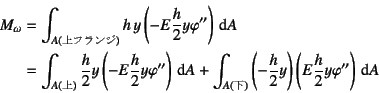
と書いてもいい。したがって式(7.45)で 定義された$\omega^*$を用いると

$$M_\omega=\int_A \omega^* \sigma_{xx}\dint A$$ (7.48)

で新しく導入した断面力を定義できることがわかる。 また，式(7.43)で表される直応力分布も

$$\sigma_{xx}=-E\omega^*\varphi''(x)$$

と書け，式(7.37)の構成関係を用いると

$$\sigma_{xx}(x,y,z)=\dfrac{M_\omega(x)}{I_\omega} \omega^*(y,z)$$ (7.49)

とも表現できる。

7.4.2 曲げねじりの境界値問題

7.4.2.1 片持ち棒のねじり

支配方程式をねじり角$\varphi(x)$で表し，いくつかの例題を 解いておこう。 つり合い式は式(7.40)で与えられるが， 式(7.3) (7.35)を代入すると ねじり角$\varphi(x)$で表したつり合い式が

$$-EI_\omega \varphi''''(x)+GJ \varphi''(x)=0$$ (7.50)

となる。簡単のために断面形状は棒の長手方向に一様であるとした。 境界条件も式(7.42)に示した通りであるが， 同様に式(7.3) (7.35) (7.39)を 代入すると

(7.51)

($i=1,2$)と書くことができる。 それぞれの断面力とねじり角$\varphi(x)$の関係も再度並べておくと

$$T_S(x)=GJ \varphi'(x), \quad M_\omega(x)=-EI_\omega \varphi''(x), \quad T_\omega(x)=M_\omega'(x)$$ (7.52)

となる。$M_\omega$は式(7.48)で 直応力と関係付けられている。したがって曲げねじりによる直応力 分布は式(7.49)で与えられ，曲げねじりをも含めた せん断応力分布が式(7.44)で算定できる。

図 7.28: 片持ち棒のねじり

最初の例は図-7.28の片持ち棒である。 つり合い式は式(7.50)あるいは

$$\varphi''''-\mu^2 \varphi''=0 \eqno{(a)}$$

と書くことができる。ここに

$$\mu\equiv\sqrt{\dfrac{GJ}{EI_\omega}}$$ (7.53)

と定義した。境界条件は，$x=0$ではねじり角もそり変位も 拘束されているので

$$\varphi(0)=0, \quad \varphi'(0)=0$$

である。一方$x=\ell$の端部はねじり外力のみが 作用したそり自由の端面なので， 式(7.53)の$\mu$を用いると

$$-\varphi'''(\ell)+\mu^2\varphi'(\ell)= \dfrac{T_0}{EI_\omega}=\mu^2\dfrac{T_0}{GJ}, \quad -\varphi''(\ell)=0$$

で与えられる。

つり合い式($a$)に $\varphi=e^{\rho x}$を代入して得る 特性方程式が $\rho^4-\mu^2\rho^2=0$となるので，$\rho=0$が 重根で$\rho=\pm\mu$が他の2根である。 したがって一般解は

$$\varphi(x)=(a+bx)+c\sinh\mu x+d\cosh\mu x$$

となる。これを上の四つの境界条件に代入して積分定数を決定すると

$$a=-d=-\dfrac{T_0}{GJ\mu}\tanh\mu\ell, \quad b=\dfrac{T_0}{GJ}, \quad c=-\dfrac{T_0}{GJ\mu}$$

となるので，ねじり角が

$$\varphi(x)=\dfrac{T_0}{GJ}x -\dfrac{T_0}{GJ\mu\cosh\mu\ell} \left\{\sinh\mu\ell-\sinh\mu(\ell-x) \right\}$$

と計算できる。第1項は式(7.9)で求められた 片持ち棒のSaint-Venantのねじりの解である。 つまり，第2項が曲げねじりを含めたことによって 生じる付加的な抵抗によるねじり角成分である。

7.4.2.2 曲げねじりとSaint-Venantのねじりの比較

上の例題を用いて， 曲げねじりと単純なSaint-Venantのねじりの分担率を， 右端のねじり角で定量比較して みよう。ねじり角の解の$x=\ell$での値は

$$\varphi(\ell)=\dfrac{T_0\ell}{GJ}\left( 1-\dfrac{\tanh\mu\... ...t), \quad \varphi_S(\ell)\equiv\dfrac{T_0\ell}{GJ} \eqno{(b)}$$

となる。$\varphi_S$はSaint-Venantのねじり抵抗のみの 場合の解である。 リンク機構等の組み立て柱でないとあり得ないだろうが， もし，曲げねじりのみで抵抗する極端な場合を想定すると， 元の方程式で$EI_\omega$に比べて$GJ$を無視すればいいから， つり合い式および境界条件に$\mu=0$を代入した 方程式で現象は支配される。つまり，つり合い式は

$$-EI_\omega \varphi''''(x)=0$$

となり，境界条件も変更される。この一般解は

$$\varphi(x)=a+bx+cx^2+dx^3$$

となるので，境界条件に代入して積分定数を決定し，この解を$\omega$の 下添え字を付けてSaint-Venantの解と区別すると

$$\varphi_\omega(x)=\dfrac{T_0}{6EI_\omega}\left( -x^3+3\ell x^2 \right)$$

と置くことができる。これに$x=\ell$を代入すると

$$\varphi_\omega(\ell)=\dfrac{T_0\ell^3}{3EI_\omega} =\dfrac{... ...ell^3}{3GJ} =\varphi_S(\ell)\dfrac{(\mu\ell)^2}{3} \eqno{(c)}$$

となる。

以上の 関係式から，$\varphi(\ell)$と， $\varphi_S(\ell)$および $\varphi_\omega(\ell)$と の関係はすべて，無次元量$(\mu\ell)$のみで表されていることが明らかだ。 そこで

$$r_\omega\equiv \sqrt{\dfrac{EI_\omega}{GJ}} =\sqrt{2 \left... ...ex{=romega@$r_\omega$}% \index{=lambdaomega@$\lambda_\omega$}%$$

の$r_\omega$を曲げねじりに関する断面の回転半径， そして $\lambda_\omega$を曲げねじりに関する断面の細長比 として定義しておくと，この無次元量は $\mu\ell=\lambda_\omega$で ある^7.3ことがわかる。 「断面の」回転半径と呼びながら$r_\omega$は材料定数比を含んでいる ので， $\lambda_\omega$も純粋に幾何学的な細長さを表しているわけでは ないが，Poisson比が同じ材料同士ならこの $\lambda_\omega$で 長さと断面寸法との比を代表させることができるので， ここでは細長比と呼んでみた。 つまりSaint-Venantのねじりと曲げねじりとは， ねじりに関する棒の細長さによって その分担率が異なってくることが予想される。

そこで，まず $\lambda_\omega\to\infty$の極限を 考えると $\tanh\lambda_\omega\to 1$となることから， 式($b$)は

$$\lim_{\lambda_\omega\to\infty}\varphi(\ell)= \lim_{\lambda_\... ...ac{\tanh\lambda_\omega}{\lambda_\omega}\right)=\varphi_S(\ell)$$

となる。 つまり細長くなればなるほど解はSaint-Venantのねじり成分が主になる。 一方 $\lambda_\omega\to 0$の場合には， まず $\tanh\lambda_\omega$をTaylor展開すれば

$$\tanh\lambda_\omega=\lambda_\omega-\dfrac{\lambda_\omega^3}{... ...\dfrac{2 \lambda_\omega^4}{15}+O\left(\lambda_\omega^6\right)$$

となる。したがって式($b$)の極限で これを考慮して式($c$)と比較すると

$$\lim_{\lambda_\omega\to 0}\varphi(\ell) =\lim_{\lambda_\omeg... ...varphi_S(\ell)\dfrac{\lambda_\omega^2}{3}=\varphi_\omega(\ell)$$

となることがわかる。つまり短い棒の解は主に曲げねじり成分が主になる。 この収束状況を図-7.29に示した。 また，曲げねじりの解とSaint-Venantのねじりのみの解および曲げねじりのみ の解との比率

$$\dfrac{\varphi(\ell)}{\varphi_S(\ell)}, \quad \dfrac{\varphi(\ell)}{\varphi_\omega(\ell)}$$

を， $\lambda_\omega$をパラメータにして プロットしたのが図-7.30である。 $\lambda_\omega$が 比較的小さく棒が短い場合には相対的にそり変位の影響を 無視できなくなるため，曲げねじり成分とSaint-Venantのねじり成分を 同時に考えなければならない[80]ことがわかる。逆に，ある程度 細長いとSaint-Venantのねじり成分が卓越している。そのため， 非常に薄肉である場合や後述の横倒れ座屈が問題になるプレートガーダ等を 除いた構造解析においては，曲げねじりを無視することが多い。 ちなみに形鋼の，例えば$380\times 100$程度の溝形鋼 で5m程度の梁を作ったとすると $\lambda_\omega$が2程度 になるため，図からも明らかなように曲げねじりとSaint-Venantの ねじりの両方を考慮しなければならない。 もちろんこの比較はねじり角に関するものであり，曲げねじりによって 生じる直応力と曲げによる直応力との比率を示したものではない。 すなわち，曲げとねじりを同時に受ける部材の場合に 曲げねじりを考慮すべきか否かについては，別途， 直応力成分の検討は必要になるので注意する必要がある。

図 7.29: 棒の細長さの影響
図 7.30: Saint-Venantのねじりと曲げねじりの比率

7.4.2.3 単純支持点での境界条件

図 7.31: 単純支持I形棒のねじり

両端単純支持されたI形断面棒の 中央に集中ねじり力を作用させた図-7.31の系を 解いてみよう。 ねじりに対する単純支持端は，図の左に 示した$y$-$z$面内のモデルのように， 回転は拘束されているものの，そりについては自由であるものとする。 したがってこの問題の境界条件は両端で

$$\varphi=0, \quad M_\omega=-EI\varphi''=0$$

となる。一方，スパン中央での連続条件は章-4の 式(4.45)で表された曲げに関するものと同様， この場合は

$$\begin{eqnarray*} && \varphi(\slfrac{\ell}{2}-)=\varphi(\slfrac{\ell}{2}+), \qua... ..._S(\slfrac{\ell}{2}+)+T_\omega(\slfrac{\ell}{2}+)\right\} = T_0 \end{eqnarray*}$$

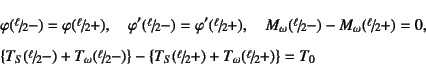
でなければならない。 一般解は前の問題と同じであるが，スパンの左右を分けて

$$\xi\equiv\ell-x, \quad \D*{( )}{\xi}=-( )'$$

という右端からの座標を新しく定義すると

$$\begin{eqnarray*} \varphi(x) &=& a+bx+c\sinh\mu x+d\cosh\mu x \quad \left(0<x<... ...erline{d}\cosh\mu\xi \quad \left(\slfrac{\ell}{2}<x<\ell\right) \end{eqnarray*}$$

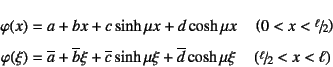
が一般解の表現となる。 左端$(x=0)$の境界条件を代入すると

$$\varphi(x)=bx+c\sinh\mu x$$

のように左側半分から二つの積分定数が残る。 同様に右端$(\xi=0)$の境界条件を代入すると

$$\varphi(\xi)=\overline{b}\xi+\overline{c}\sinh\mu\xi$$

が右半分の解の候補になる。この2式を上記の中央での連続条件に 代入すると，$\xi$に関する微係数の符号と$x$に関するその符号とが 奇数階で異なることに注意すれば，結局

$$b=\overline{b}=\dfrac{T_0}{2GJ},\quad c=\overline{c}=-\dfrac{T_0}{2GJ\mu\cosh(\slfrac{\mu\ell}{2})}$$

と未定の積分定数を決定できる。左半分だけの解を示しておくと

$$\varphi(x)=\dfrac{T_0}{2GJ}x -\dfrac{T_0}{2GJ\mu\cosh(\slfrac{\mu\ell}{2})}\sinh\mu x, \quad 0<x<\slfrac{\ell}{2}$$

となる。前の例と同様第1項がSaint-Venantのねじり成分で あり第2項が曲げねじりによる影響である。 なおこの問題は，左右の反対称性を予め考慮して おくと，図-7.32のような系を解いても 同じ解が求められることは明らかである。

1. 図-7.32の右端の境界条件を示し， これを解いて解が上の例の左半分の解に一致することを示せ。
2. 図-7.33に示したように片持ち棒の 先端に剛体を取り付け，それを偏心外力でねじった。 この問題の境界条件を示し，境界値問題を解け。中黒の丸印は， 外力ベクトル$P$の向きが紙面手前方向であることを示している。

図 7.32: 対称な系の半分
図 7.33: 片持ち棒のそりに関する境界条件

7.4.3 一般化した曲げねじり理論における断面座標・定数と応力分布

詳細は参考文献[125]等を参照して欲しいが，一般断面のねじりに 関する断面座標・断面定数・応力分布等を公式として列挙しておく。 まず，任意の薄肉断面に 拡張したSaint-Venantのねじりに関する断面座標$\Theta$は

$$\Theta(y,z)=\left\{ \begin{array}{ll} 2n & \mbox{開断面} \... ...& \mbox{閉断面} \end{array}\right. \index{=theta@$\Theta$}%$$ (7.54)

と拡張定義される。これを用いてねじり定数は

$$J\equiv\int_A \Theta^2(y,z) \dint A$$ (7.55)

で定義される。閉断面の場合，$\Theta$の定義式中の$(2n)$の影響は 第2項に比べて無視できることが多い。第2項のみを 式(7.55)に代入して求められる$J$は 式(7.19)の定義に一致する。

図 7.34: 任意薄肉断面内の$h(s)$と$h_s(s)$の定義

次に，式(7.48)の曲げねじりモーメントは

$$M_\omega(x)\equiv\int_A \omega \sigma_{xx}\dint A$$ (7.56)

と定義し直され，その断面定数のそり2次モーメントは

$$I_\omega\equiv \int_A \omega^2(n,s) \dint A$$ (7.57)

で拡張定義される。ここに，一般断面のそりに関する 断面座標$\omega$は

$$\omega(n,s) = \omega_s(n,s)-\omega_c, \quad \omega_c=\omega... ... \omega_s(n,s)=\omega^*(s)-nh_s(s) \index{=omega@$\omega$}%$$ (7.58)

と置かれ，肉厚中心線上の単位そり関数 が

$$\omega^*(s)=\left\{ \begin{array}{ll} \displaystyle\int_0^... ...frac{\dint \xi}{t(\xi)} & \mbox{閉断面} \end{array}\right.$$ (7.59)

で定義される。$\xi$は$s$に関する積分のための補助変数である。 ここに$h(s)$および$h_s(s)$は図-7.34で 定義されている。 薄肉長方形断面のときの$\omega(n,s)$の符号を替えると 式(7.22)の第2項の$\varphi'$の係数に一致する。 またI形断面に対する$\omega^*(s)$は式(7.45)に 一致している。

$s$軸の原点と$\omega_c$は任意に選べるため， 通常は$h(s)$と$h_s(s)$の原点でもあるねじれ中心点S $(y_s,z_s)$を 断面のせん断中心 と呼ばれる点に一致させることが多い。せん断中心の位置は，断面が

$$\int_A \omega y \dint A=0, \quad \int_A \omega z \dint A =0$$ (7.60)

という特性を有するように決定される。 また式(7.58)の$\omega_c$も

$$\int_A \omega \dint A=0$$ (7.61)

になるように選ばれるのが普通である。この$y_s$, $z_s$, $\omega_c$の 具体的な表現については参考文献を参照のこと。 面白いことに，ここでせん断中心と呼んでいる 点Sと節-4.6.1 (4)の 例のそれとは同一点である。

最後に直応力成分は，式(7.49)のI形断面の 場合の拡張として

$$\sigma_{xx}(x,y,z)=\dfrac{M_\omega(x)}{I_\omega} \omega(n,s)$$ (7.62)

という分布になる。一方せん断応力成分は

$$\sigma_{sx}=\left\{ \begin{array}{ll} \dfrac{T_S}{J}\Theta... ...rac{T_\omega}{I_\omega} & \mbox{閉断面} \end{array}\right.$$ (7.63)

となる。閉断面の場合の直応力とつり合うせん断応力の算定に ついては別途文献を参照のこと。閉断面の第2項の括弧内の第2項は， 閉断面に存在すべきせん断流に関連した項である。 開断面の場合の定義は式(7.44)と一致する。 また

$$\overline{Q}_\omega(n,s)=\int_{s_0}^s t(\xi) \omega(n,\xi)\dint \xi$$ (7.64)

は曲げ理論における断面1次関数に相当するものであるが，$n=0$上で あればI形断面の式(7.39)と一致する。 通常，鋼構造の部材のような薄肉断面であれば， 式(7.54)の閉断面の 場合や式(7.58)の$\omega_s$において$n$に 関する項を無視することが多い。

実際には部材の断面全体が閉断面か開断面のいずれかに なっているとは限らず， 断面の部分部分が閉じていたり開いた区間があるのが 普通である。そんな場合も上の分類を個々の区間で考えれば， 適切な断面定数や断面座標および応力分布等を求めることができる。 詳細は参考文献[125]等を参照のこと。

最新版を正確に読むためには pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。