最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。

• 7.3.1 薄肉長方形断面棒のねじり
  • 7.3.1.1 断面に発生するせん断応力の概況
  • 7.3.1.2 断面の回転とせん断流
  • 7.3.1.3 ねじりモーメントとせん断応力
  
  
• 7.3.2 薄肉開断面のSaint-Venantのねじり定数

7.3 薄肉開断面棒のねじり

7.3.1 薄肉長方形断面棒のねじり

7.3.1.1 断面に発生するせん断応力の概況

図 7.14: 薄肉長方形断面棒

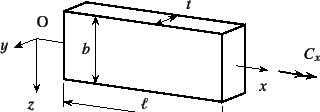
橋梁の代表的形式であるプレートガーダは，図-7.14に あるような，肉厚$t$が非常に薄い平板を複数用いて構成された断面になっている。 この断面は肉厚中心線（この図では$y$-$z$面内の$z$軸に沿う線）に 「端っこ（この図では $z=\mbox{const.}$の面つまり上下面の箇所）」が あるため，開断面 と呼ばれる。鋼構造物のほとんどすべての部材には，このような 薄肉長方形断面部分をその断面に含んでいる。 任意の薄肉断面部材のねじり抵抗を知るためには，この 長方形断面棒が

$$\ell \gg b \gg t \index{さんどいっち@サンドイッチ (typical contents of sandwich)}$$

を満足するくらい薄肉で細長い場合のねじり挙動を知る 必要がある。ただ円柱や円管とほぼ同様に，ねじりに抵抗する 内力は，この断面に発生するせん断応力，つまり直角座標系の 成分で示すと$\sigma_{xy}$と$\sigma _{zx}$の二つであると 考えてよさそうだ。

図 7.15: せん断応力分布の概況

しかし開断面の場合には，図-7.15に示した ように，そのいずれのせん断応力成分も自由表面では零になるように 分布しなければならない。 さらに，その二つのせん断応力の絶対値同士の相対的な大きさ比率は， それぞれが分布する長手方向の寸法比率に対応していると考えて よさそうである。 つまりこの場合には，非常に薄肉であることから

$$b \gg t \qquad \to \qquad \left\vert\sigma_{zx}\right\vert \gg \left\vert\sigma_{xy}\right\vert$$

と近似できそうだ。 一方このせん断応力は， ねじり外力に抵抗するような分布になっていなければ ならないから，この大きい方の$\sigma _{zx}$は$z$軸を境に左右反対称 つまり符号が異なるように分布しなければならず， 肉厚中心線$z$軸上で零になっていることが予想される。 以上の考察から，発生する応力成分に対して

$$\sigma_{xy}\equiv 0,\quad \sigma_{zx}^*\equiv \sigma_{zx}\bigr\vert _{y=0}=0$$

の2条件を仮定できそうだ。第2式の上付きの*は， 肉厚中心線上$(y=0)$での 値であることを明示するための記号である。Hookeの法則 式(3.42)にこれを代入すれば， せん断ひずみに対する仮定も同様に

(7.21)

と表現できる。

7.3.1.2 断面の回転とせん断流

図 7.16: ねじりを受けた薄肉長方形断面

円柱の場合を少し一般化し， 断面が任意の回転中心$(y_s,z_s)$回りに$\varphi(x)$だけ 回転して抵抗していると考えよう。図-7.16に その様子を示したが，この幾何学的な考察から 任意点の$y$, $z$方向変位成分が

$$\begin{array}{l} -u_y(x,y,z)= r\cos\theta-r\cos(\theta+\var... ...r\varphi\cos\theta =(y-y_s) \varphi(x) \end{array}\eqno{(a)}$$

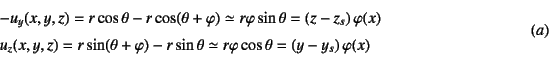
と表現できる。それぞれの式の第2式から第3式へも，$\varphi$が 微小であることを用いて近似した。

これを式(7.21a)の仮定に代入すると

$$0=2\epsilon_{xy}=\D{u_x}{y}+\D{u_y}{x} \quad\to\quad \D{u_x}{y}=-\D{u_y}{x}=(z-z_s) \varphi'(x)$$

となるから，1回積分すると

$$u_x(x,y,z)=u_x(x,0,z)+y(z-z_s) \varphi'(x) \eqno{(b)}$$

という関係になる。もう一つのひずみの仮定式(7.21b)に 式($a$)を代入すると

$$0=2\epsilon_{zx}^*=\left.\D{u_x}{z}\right\vert _{y=0} +\lef... ...\vert _{y=0} \quad\to\quad \D{u_x(x,0,z)}{z}=y_s \varphi'(x)$$

であるから，これも1回積分すると

$$u_x(x,0,z)=u_x(x,0,0)+zy_s \varphi'(x) \eqno{(c)}$$

となる。この式($c$)を式($b$)に代入して整理すると

$$u_x(x,y,z)=u(x)+(yz+zy_s-yz_s) \varphi'(x)$$ (7.22)

と$x$方向変位を得る。ここに$u(x)$は軸線上の$x$方向 変位成分$u_x(x,0,0)$を置き換えて定義したもので， 断面の$x$方向への一様な変位量である。 これに対し第2項は$y$と$z$の関数になっており， 円柱や円管とは異なり， ねじりによって断面が平面でなくなる量を 表している。これは後述の「そり」を表しているのだが， これによって直応力$\sigma_{xx}$が生じていることがわかる。 しかし，前節の閉断面の場合と同様， 薄肉長方形断面の場合にも直応力$\sigma_{xx}$は比較的小さいものとして 無視することになる。

図 7.17: ねじりによるせん断応力分布

式(7.21)の仮定をそのまま鵜呑みにすれば， 伸びひずみの$\epsilon_{xx}$以外で零でない ひずみ成分は$\epsilon_{zx}$のみであり， 式($a$) (7.22)を ひずみの定義式(3.6)に代入して

$$\epsilon_{zx}=\dfrac12\left(\D{u_x}{z}+\D{u_z}{x}\right) =y \varphi'(x)$$

となる。したがってHookeの法則式(3.42)に 代入するとせん断応力が

$$\sigma_{zx}(x,y,z)=2G y \varphi'(x) =G \left(2y\right) \varphi'(x)$$ (7.23)

と表すことができる。 これを図示したのが図-7.17の 左側の図である。$z$軸を対称軸にして反対称に線形分布をしている から$x$軸回りの抵抗モーメントが生じており，これが ねじりに抵抗する合応力を生み出すことはわかる。

図 7.18: せん断応力分布のおおまかな把握

しかしここで不合理なことに気付く。つまり，断面の 上下面 $z=\pm \slfrac{b}{2}$の自由表面で， せん断応力$\sigma _{zx}$が零になっていないことだ。 もしこの$y$方向の線形分布が正しいとしても，上下面は自由表面なの だから図-7.17の右側の図に示したように， 上下面に近づくにつれて応力は零にならないといけない。 これも初等梁理論におけるせん断応力の件と同様， 仮定を真として定式化したことによる矛盾点で ある。 そこで，前節で扱った円管をつぶしていったものが 長方形断面であろうと見当を付け， 応力分布がどのようになるべきか思考実験してみよう。

図-7.18の 左の図には前節の結果そのままを示してある。 右の図はそれをある程度つぶした 状態を模式的に捉えたものであるが，右下にある$\sigma _{zx}$の$y$方向 の分布は，上で求められたものと同様，ほぼ$z$軸を反対称 軸とした分布をするだろう。 また$\sigma _{zx}$の$z$方向分布についてはこの右の 図の右端の図のように，一様ではないが上下面で零になるような 何らかの分布をしなければならない。 最後の$\sigma_{xy}$の分布は，仮定ではすべて零と してしまったが，この図のように考えると， この上下面付近でだけはある零でない値を維持するのではないかと予想できる。 つまりこの付近は$\sigma _{zx}$も小さくなるので，$\sigma_{xy}$が それよりも小さいという最初に立てた仮定が成立しないと考えないといけない。

図 7.19: 薄肉長方形断面中のせん断流の考え方

そこで元の問題に戻って，あの便利なせん断流を思い出しながら， このつぶれた円管中に流れているであろうせん断流と比較しながら， 長方形断面で求められた結果を「解釈」して みよう。図-7.19の左図にあるように， 仮定の範囲内では線形に分布したせん断応力が発生している。 これは，$z$軸を境にした片側の三角形分布の面積に等しい$q$という せん断流が$z$軸から左右に$\slfrac{t}{3}$だけ離れた 線上すなわち分布三角形の重心の位置を流れていることを意味する。 ではマークを付した上下面付近はどうなっているだろう。 せっかくせん断流という便利な ものを考えておきながら，上下面付近ではその流れが連続していない。 この計算結果と円管をつぶしたときの思考実験とを， せん断流の概念を用いて結び付けると， 同じ図-7.19の右側に示したようなせん断流を 上下面のごく近傍のみで考えればいいのではないだろうか。 つまり，上下面付近だけは$\sigma_{xy}$のせん断抵抗が 集中して存在しており，モデルとして上下面ぎりぎりの ところに，$\sigma _{zx}$が作るせん断流と同じ大きさの$\pm y$方向の せん断流$q$を「連続して流す」ような抵抗が存在すると考えて みたらいいのではないだろうか。

この部分は非常にわかり難いとは思う。しかし，文献[126]のように 仮想仕事の原理を用いてしまうと，モデルの物理的な意味がわからなくなる。 多分にここの記述は，結果を知っている者の詭弁^7.2に なっているとは思うが， 力学的な矛盾を無くすためにせん断流を用いて解釈・説明したものである。

7.3.1.3 ねじりモーメントとせん断応力

こうすることによって，せん断流の考え方の枠の中で， 近似的なひずみや応力場への仮定とも原則として整合した理論を 構築できそうだ。 このせん断流が作る$x$軸回りのSaint-Venantのねじりモーメントを 算定すると

$$T_S=2\times\left\{\dfrac{t}{3}\times(b\times q)\right\} +2\... ...t\{\dfrac{b}{2}\times\left( \dfrac23 t\times q\right) \right\}$$

となる。右辺第1項がせん断応力$\sigma _{zx}$が作る成分であり， 第2項が前節の説明に沿って新たに加えた 上下面近傍での$\sigma_{xy}$成分による寄与分である。 図にも示したように

$$q = \dfrac12 \dfrac{t}{2} G t \varphi'$$

であるから，上式に代入して整理すると

$$T_S(x)=G\left(\dfrac{b t^3}{3}\right)\varphi'(x) \Rightarrow GJ \varphi'(x) \eqno{(d)}$$

となる。これより薄肉長方形断面のSaint-Venantのねじり定数 が

$$J=\dfrac{b t^3}{3}$$ (7.24)

であることがわかる。 また近似的にせん断応力は式(7.23)と 式($d$)から$\varphi$を消去して

$$\sigma_{zx}(x,y,z)=\dfrac{T_S(x)}{J}\times \left(2y\right)$$ (7.25)

となる。$2y$のように`2'が付くのは奇妙だが面白い。

7.3.2 薄肉開断面のSaint-Venantのねじり定数

図 7.20: 任意の薄肉開断面棒のねじり

任意の開断面棒のねじりについての詳細は参考書[125]等を 参照してもらうことにして省略し，Saint-Venantのねじりに 関する部分だけを抽出しておく。 式(7.3)と同様，Saint-Venantの ねじりモーメントと応力成分は

(7.26)

と表現でき，ねじり定数 は

$$J\equiv\int_A \Theta^2(y,z) \dint A$$ (7.27)

で定義される。 ここに$\Theta$は図-7.20に 示した座標系において

$$\Theta(y,z)\equiv 2n$$ (7.28)

で定義されている。`2'が付くのが興味深いが， ちょうど式(7.23)で`$2y$'になっていることに対応している。 この定義を用いて長方形断面の場合の$J$を計算してみると，$n=y$であるから

$$J=\int_{\slfrac{-b}{2}}^{\slfrac{b}{2}} \dint z \int_{\slfrac{-t}{2}}^{\slfrac{t}{2}} (2y)^2 \dint y = \dfrac{b t^3}{3}$$

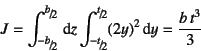
となり，式(7.24)の結果と一致する。 また式(7.26b)も式(7.25)と 一致している。

図 7.21: I形断面棒とスリットの入った円管

また図-7.21の左にあるような，長方形断面の 集合とみなすことのできる断面の場合は， 各薄板部分毎の肉厚中心線を対称軸とするようなせん断流による ねじり抵抗の合計が，全断面の抵抗になるだろうから， そのねじり定数はそれぞれの長方形断面の ねじり定数を加算するだけでいい。したがって，このI形断面の 場合のねじり定数は

$$J=\sum_{i=1}^3 \dfrac{b_i t_i^3}{3}$$

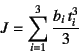
となる。 もう一つの例として，スリットの入った円管の場合を算定してみよう。 この場合は円筒座標系で $\dint A=r\dint r\dint\theta$とすればいいから， 式(7.27)の計算は

$$J=\int_{r_c-\slfrac{t}{2}}^{r_c+\slfrac{t}{2}}\dint r \int_{-\pi}^\pi r\dint\theta \left\{2\left(r-r_c\right)\right\}^2$$

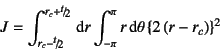
とすればよく，変数変換等の演算を施すことによって

$$J=\dfrac{2\pi}{3} r_c t^3$$

が求められる。

ところで， 薄肉円管の場合のねじり定数が$2\pi r_c^3t$であったことを 思い出すと，このスリットの入った薄肉円管断面の場合のそれとの比が

$$\dfrac{J\sub{スリット}}{J\sub{円管}} = \dfrac43 \left(\dfrac{t}{2r_c}\right)^2 \sim \dfrac{1}{(\mbox{径厚比})^2}$$

になっていることがわかる。 特に鋼構造の場合，この径厚比 の値が10程度以上になるのは普通である。したがって閉断面の円管の ねじり剛性に比べて，スリットの入った開断面部材の持つSaint-Venantの ねじり剛性が百分の一以下になってしまうこともあり得る。 開断面が閉断面に比べてねじりに対する抵抗が非常に低いのは， これが原因であり，その根本的な原因は，肉厚中心線上でのせん断応力が 零になってしまうこと，せん断応力が作るモーメントのアーム長が 肉厚程度しかないことにある。 完成系が閉断面の橋梁であっても，架設中に一時的に開断面になるような場合には 十分な注意が必要である。

1. 演習問題7-2の2番で 扱った肉厚$t$が一定の幅$b$高さ$h$の箱形断面と， 上下フランジが肉厚$t$で，幅が$b$，ウェブが肉厚$2t$で 高さが$h$のI形断面とはいずれも同じ断面2次モーメントを持つ。 後者のねじり定数を求め，薄肉の箱形とI形とのねじり定数の関係を 議論せよ。

最新版を正確に読むためには pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。