| (3.40) |
最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
図-3.8に示したように,連続体をモデル化する に当たって,材料の抵抗特性を内力という概念を仲介させて記述することに した。したがって,材料本来の変形による抵抗特性を,この内力と 変形すなわち応力とひずみの関係で表す必要がある。 材料特性を表すこのような関係式を構成方程式 あるいは構成則 と呼ぶ。 コンクリート屋さんは随分前からだが,近年では鋼構造解析屋さんの間でも, この「構成関係」という言葉を材料本来の特性のみを記述するものとして ではなく,構造系の見かけ上の抵抗力(合応力)と変形の関係に対しても頻繁に 用いるようになってきているので,初学者は注意しないといけない。 終局強度解析に断面力を用いるからだろうが, どの部分が系の境界値問題としての挙動で,どの部分が材料本来の 特性なのかについて,常に頭の中では整理・区別しておくことが重要である。 この節では材料本来の抵抗則の記述法について述べる。
最も基本的な材料特性は,理科でもよくモデルとして用いたバネの ように,外力を与えて変形させたあとで外力を取り除くと 元の形に完全に戻るような性質だろう。そういった可逆的な 材料特性を弾性 と呼んでいる。さらに抵抗力が変形に線形比例して発生する 場合には線形弾性 と呼ぶ。また,例えば引張った方向によらずその抵抗特性が同じになる 等,材料特性が方向性を有していない特性を等方性 と呼ぶ。
このような等方弾性
体の主な変形抵抗特性は,節-3.1.6で
定義したような,i) 体積変形による
抵抗と,ii) せん断変形による抵抗とに分解できる,
と考えられないだろうか。
つまり,式(3.14)の体積ひずみに比例して
式(3.38)で定義した平均応力が生じ
という抵抗特性を有しているものとする。
ここに![]() は体積弾性係数
と呼ばれる材料定数である。
さらにせん断変形については,
式(3.15) (3.39)で
定義されたひずみと応力の偏差成分同士が,
等方性のためにどの成分の間でも同じ比例関係に
あるものとしてモデル化をする。つまり
は体積弾性係数
と呼ばれる材料定数である。
さらにせん断変形については,
式(3.15) (3.39)で
定義されたひずみと応力の偏差成分同士が,
等方性のためにどの成分の間でも同じ比例関係に
あるものとしてモデル化をする。つまり
と考えてみよう。ここに![]() はせん断弾性係数
と呼ばれる材料定数である。
はせん断弾性係数
と呼ばれる材料定数である。
式(3.40) (3.41)を
式(3.39)の左辺右辺に代入し,
式(3.15)を考慮して整理すると,
応力ひずみ関係は
と書くことができる。ここに![]() は式(3.9)で
定義したKroneckerのデルタであり,
は式(3.9)で
定義したKroneckerのデルタであり,![]() と
と![]() は
は
(3.43)
と定義されLaméの定数
と呼ばれている。このような応力ひずみ関係をHookeの法則
と呼ぶ。
構造力学ではよくYoung率![]() とPoisson比
とPoisson比![]() の方を
用いるので,上で用いた定数との関係を示しておく。
の方を
用いるので,上で用いた定数との関係を示しておく。
(3.44)
他の関係は文献[25]等を参照のこと。鋼の場合,
![]() GN/m
GN/m![]() (kN/mm
(kN/mm![]() ),
),
![]() 程度の値を有している。
程度の値を有している。![]() と
と![]() の
物理的な意味は式(3.40) (3.41)から明らか
だが,
の
物理的な意味は式(3.40) (3.41)から明らか
だが,![]() と
と![]() の意味は節-3.5.2
(2)の式(3.116)がわかり易い。
の意味は節-3.5.2
(2)の式(3.116)がわかり易い。
式(3.42)の代わりに
応力成分とひずみ成分を適当な6行1列行列で表現し
とした上で
と表すことがある。ここに弾性係数行列
![]() は
は
と書くことができる。 ここでは2階・4階のテンソルを1列行列・正方行列で成分表示して いるので太字を用いていない。また行列要素の順番だけはいわゆるVoigt定数 の表記法に依っている。
またこの行列表示を用いると,Hookeの法則が
次のようなひずみエネルギ密度関数
を持っていることもわかるだろう。
さらにエネルギ的考察では,この密度関数が正値
であることが材料が安定であるための条件であるとされる。Hookeの
弾性体は安定な材料のモデルなので
を満足しなければならない。式(3.44c)を用いて,
この弾性係数行列
![]() を
を![]() と
と![]() で表しておくと,
上の安定条件は
で表しておくと,
上の安定条件は![]() であることに加えて,各小行列の
であることに加えて,各小行列の
すなわちPoisson比がとり得る範囲は
でなければならないことがわかる。
通常の材料ではPoisson比は正の値と考えられ,完全流体やゴムの
ような非圧縮性
材料では
その値が![]() (したがって
(したがって![]() と
と![]() は
は![]() )になる。
負のPoisson比を持つ材料は複合材料
で作ることができる。
)になる。
負のPoisson比を持つ材料は複合材料
で作ることができる。
等方弾性はたった二つの材料定数でその特性を代表させられた。 その結果を次のようにして確かめてみよう。 式(3.42)を
(3.50)
と表すこともできることは,式(3.9)のKroneckerの
デルタの定義を用いて演算してみれば簡単に示すことが
できる。![]() を弾性係数テンソル
を弾性係数テンソル![]() の成分
と呼ぶ。一方,ある回転させた他の座標系での成分同士の関係は
の成分
と呼ぶ。一方,ある回転させた他の座標系での成分同士の関係は
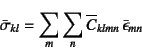
と書くことができる。この右辺に式(3.12)の逆関係を
代入すると
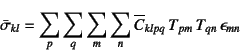
という関係になる。これを式(3.36)に
代入することによって
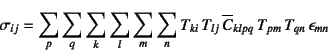
となる。これと元の式(3.50a)を等値することにより
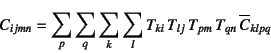
と,弾性係数テンソルの座標変換則を得る。座標変換行列が
正規直交行列であることを考慮すれば,この逆関係は
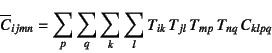
となるが,これに式(3.50b)を代入すると実は
であることを示すことができる。すなわち,Hookeの法則の 弾性係数テンソルは座標をどんなに回転させても成分そのものが 全く変化しないことを意味している。 等方材料の抵抗則を表しているのだから当然だ。
このことから,式(3.50b)の
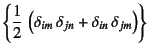 と
と
![]() あるいは
あるいは
| (3.51) |
を成分に持つ4階のテンソルを等方テンソル
と呼ぶ。
後者のテンソル![]() と
と![]() はそれぞれせん断抵抗と
体積抵抗に対応した成分と考えてもよく,等方弾性係数は
はそれぞれせん断抵抗と
体積抵抗に対応した成分と考えてもよく,等方弾性係数は
とも表現できる。また![]() は次の意味で部分的には
等方的ではない(せん断的な)ことから,
は次の意味で部分的には
等方的ではない(せん断的な)ことから,![]() と
と![]() は次の意味で
直交3.12している。
は次の意味で
直交3.12している。
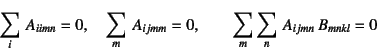 |
(3.53) |
この直交性が成立することから,式(3.52)の
逆テンソルである等方弾性コンプライアンステンソル
成分は
と表現できる。
すなわち,二つの直交する等方テンソル![]() と
と![]() の
係数だけを逆数にした関係になる。ちなみに,コンプライアンスは
式(3.50b)の逆の
の
係数だけを逆数にした関係になる。ちなみに,コンプライアンスは
式(3.50b)の逆の
という関係の係数である。あるいは行列で表すと
となる。
等方弾性だけではなく,一般的には応力ひずみ関係を式(3.50a)のように
と表すことができ,一般化されたHookeの法則
と呼ばれる。応力テンソルもひずみテンソルも9個の成分を持つから,
この弾性テンソル![]() は81個の
成分でできていることになるが,応力テンソル成分とひずみテンソル成分が
対称であることから,弾性テンソル成分は
は81個の
成分でできていることになるが,応力テンソル成分とひずみテンソル成分が
対称であることから,弾性テンソル成分は
| (3.58) |
という対称性を持つように定義することができる。
したがって,独立な成分の数は36個になる。
ちょうど,式(3.46)の要素がすべて非零で
非対称の場合に相当する。
ただし,もしこの弾性体が式(3.47)の
ようなエネルギ密度関数を有している材料としてモデル化できるなら
が成立するような対称性を持つテンソルになる。 こうなると結局,弾性テンソルは21個の独立な材料定数で表される。 ちょうど,式(3.46)の要素がすべて非零で 対称の場合に相当する。 つまり,一般的な異方性 材料は36個ないし21個の材料定数で構成則を記述できる。 さらに,直交する三つの面に対して対称な材料特性(微視構造等)を 持つ直交異方性 材料の場合には,対称性によって独立な定数が減じて12個になる。 ちょうど,式(3.46)の非零の要素がすべて独立で, かつ非対称な場合に相当する。2次元なら ちょうどハンカチやむしろのように,布目や 藁が直交して配置された平面の, 辺方向と対角方向との抵抗が違っているものを思い浮かべるといいかもしれない。 この場合も,もしエネルギ密度関数が存在するモデルなら9個が独立になる。 これがちょうど,式(3.46)の非零の要素が独立で 対称な場合に相当する。 さらに,もう1種類の対称面がある(ちょうど立方晶のような)場合には, 独立な定数が3個になり,最終的に方向性が無くなった 場合には2個の独立な定数しか必要がなくなる。 これがまさに式(3.46)の 等方弾性体である[51,127]。
具体的に表すために
と表すことがある。ここに直交異方性材料の弾性係数行列![]() は
は
と書くことができる。この行列の要素はいわゆるVoigt定数
と呼ばれる。
一般には式(3.59)の対称性は
成立するとは限らないので,
弾性定数行列が非対称
![]() であることには注意する。
であることには注意する。
等方弾性の場合はVoigt定数で独立なのは2個だけであり
という関係になる。これに対して独立な定数が3個の
材料は,単結晶ならAlやCu, Fe, Ni等の立方晶
であり
| (3.62) |
が独立な非零の定数である。
一方,MgやZnのような単結晶は六方晶
である。これは,
ある一つの方向の格子構造が他の2方向の格子構造とは異なる3.13と考えればいい。
この場合には,その特殊な格子構造方向の軸の
回りに(その軸を法線とする面内のみに)だけ等方性を有するため,
独立な材料定数は6個(
![]() の場合)ないし5個
(
の場合)ないし5個
(![]() の場合)になる。
例えば
の場合)になる。
例えば![]() 方向がその特徴的な方向なら
方向がその特徴的な方向なら
の中の5個ないし6個が独立な非零の定数である。 このような性質を横等方性 と呼ぶ。節-3.5.2 (4)で 紹介する1方向の繊維補強材は,巨視的にその性質を有している材料である。
さて式(3.60)の逆関係を
| (3.64) |
と表すと,一般的な直交異方性材料のコンプライアンス行列![]() は
式(3.56)3.14を一般化して
は
式(3.56)3.14を一般化して
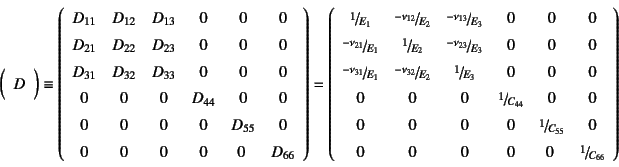 |
(3.65) |
と書くことができる。
この![]() や
や![]() は一般化されたYoung率とPoisson比である。
そこで,横等方性材料の場合の諸量を求めてみると
は一般化されたYoung率とPoisson比である。
そこで,横等方性材料の場合の諸量を求めてみると
と定義しておくと
であり,さらに
のような関係がある。
例えば,
森・田中のアプローチを用いて,1方向に長い炭素繊維が配置されている
複合材料(CFRP)の
巨視的な弾性テンソルをモデル化してみよう。
文献[56]で用いられた炭素繊維補強ポリマーの
積層板としての材料定数は,後述の式(3.122)のように
弾性テンソル成分と関係付けられているが,
その実測値が![]() GN/m
GN/m![]() ,
, ![]() ,
,
![]() GN/m
GN/m![]() ,
, ![]() GN/m
GN/m![]() (
(![]() の添え字は`12'となって
いるが,これは
の添え字は`12'となって
いるが,これは![]() ではなく
ではなく![]() の方)と与えられている。
そこで,森・田中アプローチを用いて,このような巨視的な
炭素繊維補強ポリマー積層板の弾性定数に一致するような,母材と
介在物の材料定数を同定してみる。炭素繊維は無限に長い円柱として
モデル化できるものとし,その体積比率を50%としてみた。
その結果,
母材のビニルエステル樹脂のYoung率とPoisson比が
の方)と与えられている。
そこで,森・田中アプローチを用いて,このような巨視的な
炭素繊維補強ポリマー積層板の弾性定数に一致するような,母材と
介在物の材料定数を同定してみる。炭素繊維は無限に長い円柱として
モデル化できるものとし,その体積比率を50%としてみた。
その結果,
母材のビニルエステル樹脂のYoung率とPoisson比が
![]() GN/m
GN/m![]() ,
,
![]() で,
介在物の炭素繊維の弾性定数が
で,
介在物の炭素繊維の弾性定数が
![]() GN/m
GN/m![]() ,
,
![]() であればいいことがわかった。
なお,これを用いたとき,巨視的な積層板の
材料定数のうちの
であればいいことがわかった。
なお,これを用いたとき,巨視的な積層板の
材料定数のうちの![]() は0.0210となった。
この結果を式(3.61)の形で示すと
次のようになる。
は0.0210となった。
この結果を式(3.61)の形で示すと
次のようになる。
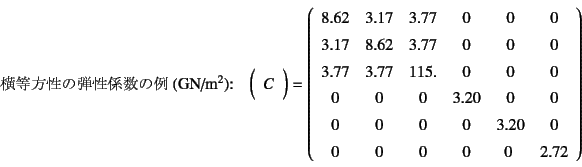
なお,ここでは炭素繊維が![]() 方向に整列しているものとした。
まさに,式(3.63)の関係がすべて成立し,さらに
弾性テンソルが対称(
方向に整列しているものとした。
まさに,式(3.63)の関係がすべて成立し,さらに
弾性テンソルが対称(![]() ,
,
![]() )であることが明らかである。
)であることが明らかである。
ついでに,節-3.5.2 (4)で
紹介する,2方向(ここでは![]() ,
, ![]() 方向)に同じ仕様の繊維を
配置した補強材は,巨視的には
方向)に同じ仕様の繊維を
配置した補強材は,巨視的には
| (3.69) |
のような材料になる。この場合のコンプライアンスを求めると
と定義しておくと
であり,さらに
のような関係がある。
ここは読み飛ばしてもいいが,
物体中の点
![]() に大きさ
に大きさ![]() の
集中外力が作用しているとき,式(3.22)の
つり合い式にある分布外力
の
集中外力が作用しているとき,式(3.22)の
つり合い式にある分布外力![]() を
を
と表すことができる。
この
![]() はDiracのデルタ関数
と呼ばれる。
その定義については索引から探してもらうことにして省略すると,
最も重要な性質は
はDiracのデルタ関数
と呼ばれる。
その定義については索引から探してもらうことにして省略すると,
最も重要な性質は
になるということである。
この集中外力だけが作用したときに生じた応力と変位を
それぞれ
![]() ,
,
![]() と
表すことにすると,つり合い式と境界条件は
と
表すことにすると,つり合い式と境界条件は
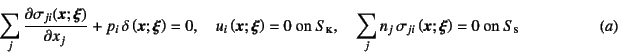
となる。
ここに表面![]() のうち,
のうち,![]() は変位を固定した境界であり,
は変位を固定した境界であり,![]() は
表面外力を与えていない自由表面で,
は
表面外力を与えていない自由表面で,
![]() ,
,
![]() である。
一方,同じ境界条件が与えられた同じ物体の
である。
一方,同じ境界条件が与えられた同じ物体の
![]() に
集中外力
に
集中外力![]() のみが作用したとすると,そのつり合い式と境界条件は
のみが作用したとすると,そのつり合い式と境界条件は
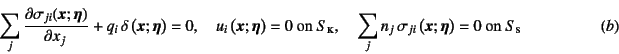
である。
そこで,後述の節-3.4で
定義される仮想仕事を考察してみよう。
すなわち,式(![]() )のつり合い式にもう一つの問題の
変位
)のつり合い式にもう一つの問題の
変位
![]() を乗じて仕事を算定して
物体全体で合計すると
を乗じて仕事を算定して
物体全体で合計すると
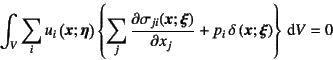
となる。第1項にGaussの発散定理を用い,第2項に式(![]() )を用いると
)を用いると
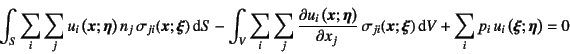
となる。式をじっくり眺めて比べて欲しい。
式(![]() )の力の境界条件と式(
)の力の境界条件と式(![]() )の変位の境界条件を
第1項に代入すれば,それは零になる。第2項の被積分関数に
ある応力が対称であることとひずみの定義式(3.6)とを考慮すれば,
結局上式は
)の変位の境界条件を
第1項に代入すれば,それは零になる。第2項の被積分関数に
ある応力が対称であることとひずみの定義式(3.6)とを考慮すれば,
結局上式は
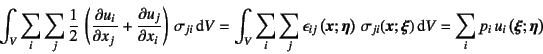
となる。これに式(3.57)の応力ひずみ関係を代入すると
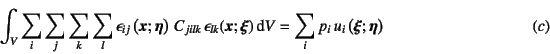
と表すことができる。
これと全く同じような仮想仕事を,式(![]() )のつり合い式に
式(
)のつり合い式に
式(![]() )の問題の変位
)の問題の変位
![]() を乗じて算定すると,
最終的に
を乗じて算定すると,
最終的に
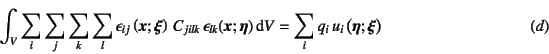
を得る。この両式(![]() ) (
) (![]() )を辺々引き,左右を入れ替えると
)を辺々引き,左右を入れ替えると
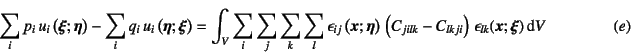
という関係が成立することがわかる。
そこで,もしエネルギ密度関数が存在するモデルで材料特性を表すことが
できるのであれば,式(3.59)の
対称性が成立する(自己随伴系になる)ので,
上式(![]() )の右辺が零になることから,結局
)の右辺が零になることから,結局
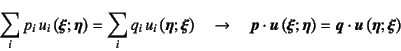
となる。これはBettiの相反定理
と呼ばれる。さらに,![]() も
も![]() も任意であるし,
もし
も任意であるし,
もし
![]() であれば
であれば
という関係が成立し,これはMaxwellの相反定理
と呼ばれる。
つまり,ある物体の
![]() に単位の
集中外力を作用させたときの
に単位の
集中外力を作用させたときの
![]() の位置の変位は,
逆に
の位置の変位は,
逆に
![]() に同じ向きの単位の
集中外力を作用させたときの
に同じ向きの単位の
集中外力を作用させたときの
![]() の位置の変位と
等しくなることを意味している。
ちょっと不思議でなかなか信じられないような結論であるが,
これが自己随伴系
が持つ著名な特性である。
逆に考えると,複合材料のように内部に微視構造が存在して
複雑な異方性が存在する材料の場合には,
式(3.59)の対称性が
成立しない場合があり,そのときには相反定理は成立しない。
随伴系
のひずみ
の位置の変位と
等しくなることを意味している。
ちょっと不思議でなかなか信じられないような結論であるが,
これが自己随伴系
が持つ著名な特性である。
逆に考えると,複合材料のように内部に微視構造が存在して
複雑な異方性が存在する材料の場合には,
式(3.59)の対称性が
成立しない場合があり,そのときには相反定理は成立しない。
随伴系
のひずみ
![]() で表した
見かけ上のつり合い式と力学的境界条件は
で表した
見かけ上のつり合い式と力学的境界条件は
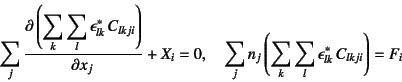
となり,一般(
![]() の場合)には物理的な意味は無い。
の場合)には物理的な意味は無い。
この節の内容は章-9で詳述し, それ以外の構造力学の章ではほとんど使わないため, 読まなくても構わないが,頭の体操にはなると思う。 あるいは,構造力学を初めて学ぶ人の場合には,ここは読まずに 平面問題の節-3.5.2を眺めて次の章に移ってもいい。 さて,針金を思いっきり曲げると元の形には戻らなくなる。 こういった非可逆的特性を非弾性 と呼ぶが,元の形との差である残留変形が時間と共には変化しない場合, その変形量を塑性変形 と呼ぶ。 塑性は弾性とは大きく異なり,1)状態を定義する関係式と,2)変形の変化則を 定義する関係式との二つを規定する必要がある。
最初に非可逆変形の例として,摩擦とそれが切れたときのすべり移動を
少し考察してみよう。図-3.14に示したのは,
ある斜めの力![]() で消しゴムを押している状況である。
この床と消しゴムの間の静止摩擦係数
を
で消しゴムを押している状況である。
この床と消しゴムの間の静止摩擦係数
を![]() とする。消しゴムがすべり始める可能性は
とする。消しゴムがすべり始める可能性は
で与えられるが,実際にはすべらないものと考えて欲しい。
この状態で,力の大きさや向きをちょっとだけ変化させた(![]() )とき,
例えば
)とき,
例えば
![]() とか
とか
![]() のような
変化が与えられたときに,もし
のような
変化が与えられたときに,もし![]() が正になろうとする
場合(
が正になろうとする
場合(![]() )にすべり始めると考えてみよう。
)にすべり始めると考えてみよう。
例えば
![]() ,
, ![]() とした場合には
とした場合には
となるから,![]() の方向である床方向,
つまり
の方向である床方向,
つまり![]() の方向にすべり始める。
では次に押さえつける力を緩めるように
の方向にすべり始める。
では次に押さえつける力を緩めるように
![]() ,
, ![]() と
した場合は,もっと弾性との差が明確で
と
した場合は,もっと弾性との差が明確で
となるので,このときもすべり始めるが,すべる方向は変動![]() とは
関係がなく,それと直交する床方向つまり
とは
関係がなく,それと直交する床方向つまり![]() の方向である。
では
の方向である。
では
![]() ,
, ![]() の場合はどうだろう。
このときは
の場合はどうだろう。
このときは
のように,摩擦が切れる条件を満足したままなので,果たしてすべるか
どうかはわからない。最後に力の向きを変えて
![]() と
した場合には,
と
した場合には,
![]() ,
,
![]() ならば
ならば
となり,このときも![]() の方向にすべり始めることになる。
の方向にすべり始めることになる。
このように,状態を規定する関数![]() が負であれば消しゴムが
弾性変形するだけであり,関数
が負であれば消しゴムが
弾性変形するだけであり,関数![]() が零になったときに,非可逆的な運動が
生じる可能性が発生する。そして,その関数が増えようとしたときに,
実際に非可逆的なすべり運動が生じるのである。しかし,その運動の向きは,
外力変動や作用の向きの変動とは無関係に,常に床に沿った方向,
言い換えればせん断力
が零になったときに,非可逆的な運動が
生じる可能性が発生する。そして,その関数が増えようとしたときに,
実際に非可逆的なすべり運動が生じるのである。しかし,その運動の向きは,
外力変動や作用の向きの変動とは無関係に,常に床に沿った方向,
言い換えればせん断力![]() の方向に,つまり
の方向に,つまり
のように生じることになる。
これに対して弾性の場合はどうだろう。
例えば![]() を増やす(
を増やす(![]() )と,消しゴムは
鉛直方向にさらに縮もうとするだろう。
また摩擦抵抗している状態(
)と,消しゴムは
鉛直方向にさらに縮もうとするだろう。
また摩擦抵抗している状態(![]() )で
)で![]() を増やすと,
消しゴムは歪もうとするだろう。つまり,
弾性状態(
を増やすと,
消しゴムは歪もうとするだろう。つまり,
弾性状態(![]() )あるいは非可逆運動が生じない場合(
)あるいは非可逆運動が生じない場合(![]() )には
弾性変化しか生じず,
しかもその変形は外力変動や作用の向きの変動に直接関係するのである。
)には
弾性変化しか生じず,
しかもその変形は外力変動や作用の向きの変動に直接関係するのである。
まず必要なのは,どういう状態に至った時点で塑性変形が生じ始めるのか 規定する条件である。そのような条件を降伏条件 と呼ぶ。鋼等の構造用の等方均質な(多結晶系)金属材料に対象を限った場合, 一般に静水圧では塑性変形は発生しないと考えていい。 すなわち鋼球を海底深く沈めた場合その直径は小さくなるが, その変形は弾性的であり,海面に戻すとその直径は元に戻り, 残留変形が生じないのである。 したがって,塑性変形特性を支配しているのは,せん断変形および せん断抵抗が主であると考えるのが適切であろう。 ただし,詳細は省略するが,残留変形 と呼ばれる元に戻らない変形成分は変形履歴に従って累積する。 そのため,状態を定義する降伏条件を変形あるいはひずみで規定することは 適切ではない。
このように考えると,せん断抵抗成分を代表している応力,
すなわち,式(3.39)で定義した
偏差応力で降伏条件を与えるのが適切であろう。
ただし,ある座標系における偏差応力テンソルの「成分」そのもので
その条件を与えることが相応しくないことは明らかである。
というのも,材料の性質は,それを観察あるいは記述している人間の都合で
導入した座標系には依存しない
はず3.15だからである。
したがって,座標とは関係の無い量として,主応力3.16あるいは偏差応力の不変量を用いるのが適切であろう。そこで,
式(3.39)の偏差応力の不変量を,
式(3.35)の応力の不変量に準じて算定すると,
その定義から明らかなように第1不変量(通常![]() と記すことが多い)は
零
と記すことが多い)は
零
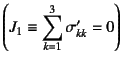 になる。
そして第2不変量は
になる。
そして第2不変量は
と定義できる。
ベクトルのノルムからの類推をすると,
![]() は
偏差応力の一種のノルム(絶対値)と考えてもよさそうだ。
特別な例として,
は
偏差応力の一種のノルム(絶対値)と考えてもよさそうだ。
特別な例として,![]() -
-![]() 面内の単純なせん断応力状態で
ある場合を考えると,応力テンソル成分は
面内の単純なせん断応力状態で
ある場合を考えると,応力テンソル成分は![]() のみが非零なので,
これを上式に代入すると
のみが非零なので,
これを上式に代入すると
![]() となる。
このことからも,
となる。
このことからも,
![]() が
せん断抵抗を代表した指標であることがわかる。
そこで塑性モデルの一つとして,この
が
せん断抵抗を代表した指標であることがわかる。
そこで塑性モデルの一つとして,この
![]() がある
限界値に達したときに塑性変形が発生すると考えてみよう。つまり
がある
限界値に達したときに塑性変形が発生すると考えてみよう。つまり
が降伏条件になると考えるのである。
ここに,![]() を初期せん断降伏応力
と呼ぶ。
例えば
を初期せん断降伏応力
と呼ぶ。
例えば![]() -
-![]() 面内の単純なせん断応力状態では,
上の降伏条件式は単純な関係
面内の単純なせん断応力状態では,
上の降伏条件式は単純な関係
![]() になる。
この降伏条件は別名Misesの降伏条件
とも呼ばれている。
になる。
この降伏条件は別名Misesの降伏条件
とも呼ばれている。
あるいは鋼の引張り試験のように,例えば![]() 方向の
応力
方向の
応力![]() だけが非零である場合には,
式(3.75)は
だけが非零である場合には,
式(3.75)は
![]() と
なるので,降伏条件は
と
なるので,降伏条件は
![]() となる。
このことから,引張り降伏
応力
となる。
このことから,引張り降伏
応力
![]() とせん断降伏応力が
とせん断降伏応力が
という関係にあることがわかる。
そのため,式(3.75) (3.76)の代わりに
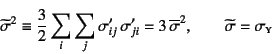 |
(3.78) |
のように降伏条件を
定義している場合もある。この
![]() は相当応力
と呼ばれている。
構造解析での降伏の代表値としては,この引張り降伏応力の方が
よく用いられる。
ちなみに,三つの主応力方向すべてと等しい角をなす面上の
せん断応力成分つまり八面体
応力
は相当応力
と呼ばれている。
構造解析での降伏の代表値としては,この引張り降伏応力の方が
よく用いられる。
ちなみに,三つの主応力方向すべてと等しい角をなす面上の
せん断応力成分つまり八面体
応力![]() [25]は
[25]は
![]() と
と
| (3.79) |
という関係にある。
このように, 塑性変形が主にせん断で支配されていることからも類推できるように, 塑性変形は物体内部の非可逆的なすべり変形でモデル化できそうだ。 つまり,図-3.15に模式的に 示したように,外力の作用によって物体内部に生じた応力の組み合わせが, ある特定な向きを持った面上3.17での 摩擦抵抗を無力にし,すべりの発生3.18が可能になるのである。 このように,ある面上の応力状態がすべりを 可能にした場合に「降伏条件が満足された」と判断でき, そこに塑性変形が生じると考えるのである。 したがって,そのあとのすべり変形の向きは,この面の向きで決まってしまう。
降伏条件を満足したあとの抵抗特性の記述には,非線形的な全応力と 全ひずみ関係で表す全ひずみ理論 と,ひずみ速度が塑性ポテンシャル で与えられる等とする流れ理論 とがある。ここではその詳細は述べないが, 前者は単調載荷状態での解析上の取り扱いが比較的楽な反面, 応力とひずみの一対一関係が無い弾塑性現象をうまく表しきれない。 一方後者は,応力速度(増分)とひずみ速度(増分)を 関係付けた増分理論 になり,連続体力学で広く用いられるモデルの基本則である。 このように,現在の状態からどのように発展するのか, つまり増分や変化が生じるのか記述したものを流れ則 あるいは発展則 と総称している。
流れ則の記述の歴史は,文献[34]からそのまま引用すると
まずSaint-Venantが1870年に
と洞察し,Lèvy (1871)とMises (1913)が同様に
になるとした。ここにはひずみの増分3.19あるいはひずみ速度である。その後Prandtl (1924)とReuss (1930)は, 弾性と塑性を分離して考える必要があるとして
である とした。
つまり永久変形の変化は偏差応力と同じ方向に発生しようとする。
偏差応力が物理的にはせん断応力であることを思い出すと,
この流れ則の式(3.80)は
摩擦とすべりで説明した式(3.74)と
同じで,永久変形はせん断変形であることがわかる。
大事なことは,式(3.80)の左辺のひずみには
増分を示すドットがついているのに対し,右辺の応力にはそれが
無いということである。文献によっては右辺の![]() にドットを
付けているものもある。
にドットを
付けているものもある。
さて,
![]() はひずみ増分のうちの
塑性成分であり,弾性成分を
はひずみ増分のうちの
塑性成分であり,弾性成分を
![]() と記したときに,
総ひずみ増分が
と記したときに,
総ひずみ増分が
のように分解される。![]() は速度あるいは
変位増分である。これは,変形勾配の乗算則を
載荷の瞬間毎に「ある参照状態」において増分をとったものであり,
[近似的に[93]/厳密に[58]]成立するもので,
本質的には乗算則と整合する考え方である。
また式(3.80)は粘性の記述によく似ているが,
粘性とは異なり,右辺の
は速度あるいは
変位増分である。これは,変形勾配の乗算則を
載荷の瞬間毎に「ある参照状態」において増分をとったものであり,
[近似的に[93]/厳密に[58]]成立するもので,
本質的には乗算則と整合する考え方である。
また式(3.80)は粘性の記述によく似ているが,
粘性とは異なり,右辺の![]() は応力状態と応力増分に
依存した比例パラメータであり,単純な材料パラメータではないことに
注意すべきである。
また式(3.81)から明らかなように,
総ひずみ増分は式(3.16)を増分ひずみで
表した適合条件を満足する適合ひずみであるが,
その弾性成分と塑性成分は共に適合ひずみではない。
は応力状態と応力増分に
依存した比例パラメータであり,単純な材料パラメータではないことに
注意すべきである。
また式(3.81)から明らかなように,
総ひずみ増分は式(3.16)を増分ひずみで
表した適合条件を満足する適合ひずみであるが,
その弾性成分と塑性成分は共に適合ひずみではない。
この式(3.80)等から,
塑性が弾性と本質的に異なっていることが明らかである。
すなわち,塑性の場合にはSaint-Venantが記述したように,
「塑性ひずみ増分が偏差(せん断)応力そのものと共軸であろうとする」
のに対し,
弾性の場合には式(3.40) (3.41)から明らかなように,
「弾性ひずみは応力そのものと,また
弾性ひずみ増分は応力増分と共軸であろうとする」
ことになる。
ここに,
![]() ,
,
![]() はそれぞれ
式(3.14)で定義した体積ひずみの
弾性成分と塑性成分であり,
はそれぞれ
式(3.14)で定義した体積ひずみの
弾性成分と塑性成分であり,![]() は
式(3.38)で定義された平均応力である。
言い換えると,変形の増分に着目したときに,
「弾性ではその増分変形の向きも大きさも応力増分に直接関係している」が,
「塑性では増分変形の向きは応力そのものの向きで支配されるが,
増分変形の大きさは応力増分にも関係している」ことになる。
これは,次のような塑性の「内部メカニズム」を考えると,
少しはわかり易いかもしれない。
は
式(3.38)で定義された平均応力である。
言い換えると,変形の増分に着目したときに,
「弾性ではその増分変形の向きも大きさも応力増分に直接関係している」が,
「塑性では増分変形の向きは応力そのものの向きで支配されるが,
増分変形の大きさは応力増分にも関係している」ことになる。
これは,次のような塑性の「内部メカニズム」を考えると,
少しはわかり易いかもしれない。
つまり,図-3.15を用いて説明したように, ある面上で「降伏条件」が満足された場合, その面の向きでそのあとの塑性変形の向きは既に決定されてしまっていると考える。 したがって,その後さらに外力を増やそうとした場合, このすべり面上でのすべり変形しか3.20生じようとはしないだろう。 このことから,その増分変形の向きは すべり出そうとするすべり面の向きで決定され,結局, 増分変形の向きは応力状態そのもので支配されることになる 一方で,図-3.16のように, 実際にすべり変形(増分)が生じるかどうかは, そこに発生する応力増分の向きと大きさに依存する。 後半の現象が「流れ則」の部分であり,前半が「降伏条件」に相当する。
降伏条件が式(3.76)で定義され,
流れ則が式(3.80)で与えられる場合の,
等方材料の構成方程式を求めておこう。
ここでは具体的な例として,降伏条件を
と設定しよう。初期降伏後の履歴依存を明示するために,
せん断降伏応力![]() を塑性ひずみの関数3.21として定義しておく。
つまり,塑性ひずみは変形の非可逆的
履歴を記憶している状態変数と考えればいい。
この
を塑性ひずみの関数3.21として定義しておく。
つまり,塑性ひずみは変形の非可逆的
履歴を記憶している状態変数と考えればいい。
この![]() を降伏関数
と呼ぶ。
したがって,例えば単調に載荷し続けて塑性変形を発生させ続けた場合には,
上式(3.82)の
を降伏関数
と呼ぶ。
したがって,例えば単調に載荷し続けて塑性変形を発生させ続けた場合には,
上式(3.82)の![]() は零を満足し続ける。
したがって「載荷」
という状況は
は零を満足し続ける。
したがって「載荷」
という状況は
| (3.83) |
という条件で定義できそうである。
これに対し,一旦降伏した材料の外力が取り除かれ,
材料が弾性に戻る「除荷」
の場合には,![]() は不変なまま降伏条件を満足しなく
なろうとするので
は不変なまま降伏条件を満足しなく
なろうとするので
| (3.84) |
で定義できそうだ。ただし,除荷直後の弾性状態では![]() に3.22なる。同じ応力状態で2種類の変化が
可能なことも,構成方程式を増分で与える必要がある理由の一つである。
に3.22なる。同じ応力状態で2種類の変化が
可能なことも,構成方程式を増分で与える必要がある理由の一つである。
載荷され続ける状態では,上記のように降伏条件![]() は満足され続けるので,
式(3.82)の増分は零となり
は満足され続けるので,
式(3.82)の増分は零となり
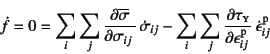 |
(3.85) |
を常に満足していることになる。この条件は整合条件
と呼ばれている。
右辺の塑性ひずみ増分に式(3.80)の流れ則を代入し,
さらに
という関係を第1項に代入すれば
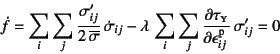
となるので,これから
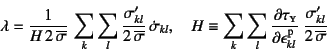
となる。ここでは章-9での議論と
合わせるために,
![]() で調整したもので
で調整したもので![]() を
定義しているが,この
を
定義しているが,この![]() は硬化係数
と呼ばれる材料パラメータである。
つまり,変形履歴においてせん断降伏応力
は硬化係数
と呼ばれる材料パラメータである。
つまり,変形履歴においてせん断降伏応力![]() が
どのように変化するか(硬化則)
という材料特性を実験等で求めておけば,
硬化パラメータ
が
どのように変化するか(硬化則)
という材料特性を実験等で求めておけば,
硬化パラメータ![]() を具体的に表現することができる。
この
を具体的に表現することができる。
この![]() を流れ則に代入することによって,増分ひずみの塑性成分が
を流れ則に代入することによって,増分ひずみの塑性成分が
と表されることになる。
さて,弾性部分がHookeの法則の式(3.55)を
増分同士の関係に直したもので
のように与えられることにしよう。
その関係と上式(3.86)を
式(3.81)に代入すれば,増分応力と増分ひずみの
間を関係付ける弾塑性関係が
と求められる。この逆関係を求めると
となる。ここに![]() は式(3.50b)で
定義された弾性係数である。式(3.88)
(3.89)右辺の塑性に関する項は,
降伏条件が成立(
は式(3.50b)で
定義された弾性係数である。式(3.88)
(3.89)右辺の塑性に関する項は,
降伏条件が成立(![]() )している場合にのみ考慮し,
弾性状態(
)している場合にのみ考慮し,
弾性状態(![]() )では無視する。
)では無視する。
構造力学では古典的に完全塑性
モデルを用いることが多く,降伏応力を定数とし,
降伏条件が満足されたあとも硬化
等が起こらず(![]() に相当する),その同じ条件が満足され続けるものとしている。
詳細については他文献等を参照のこと。
梁や板の基礎的な構造力学では応力状態が1軸状態であることが
普通であり,この文書のほとんどの箇所では複雑な塑性理論は用いない。
塑性論については,章-9や
文献[92,93]等を参照のこと。
に相当する),その同じ条件が満足され続けるものとしている。
詳細については他文献等を参照のこと。
梁や板の基礎的な構造力学では応力状態が1軸状態であることが
普通であり,この文書のほとんどの箇所では複雑な塑性理論は用いない。
塑性論については,章-9や
文献[92,93]等を参照のこと。
塑性とは異なり,非弾性変形が時間と共に変化する性質を粘性
と呼ぶ。これは式(3.80)に似た抵抗則で,1次元状態の
モデルの場合は
| (3.90) |
となる。ここに![]() は材料パラメータである。
例えば,外力が作用して応力が一定の状況にあっても,ひずみが時間と共に
大きくなることになる。このような現象をクリープ
と呼ぶ。逆に,変形が一定の状況で応力が変化してしまうこともある。
それを応力緩和
と呼んでいる。著者らは粘性については苦手なので,このくらいの記述に留める。
は材料パラメータである。
例えば,外力が作用して応力が一定の状況にあっても,ひずみが時間と共に
大きくなることになる。このような現象をクリープ
と呼ぶ。逆に,変形が一定の状況で応力が変化してしまうこともある。
それを応力緩和
と呼んでいる。著者らは粘性については苦手なので,このくらいの記述に留める。
材料の抵抗則は,物理的解釈に基づいて何らかの材料モデルを作り,
材料試験結果に基づいてその材料パラメータを同定するのが
一般的な方法である。
注意しないといけないのは,材料試験が行われる座標系は,試験する
人間の都合で特別に限定されていることである。
それに対して材料モデルの方は,特に等方材料であれば座標系には
依存しない表現になっていないといけない。
簡単な例を挙げると,![]() や
や![]() のような
スカラー関数(テンソルの不変量)を用いることや,
主値(主応力や主ひずみと主方向)を用いてモデルを構築するのが
望ましいことになる。
そのため,塑性の説明でも相当応力
のような
スカラー関数(テンソルの不変量)を用いることや,
主値(主応力や主ひずみと主方向)を用いてモデルを構築するのが
望ましいことになる。
そのため,塑性の説明でも相当応力
![]() 等が
用いられていたのである。
等が
用いられていたのである。