最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。

3.4 二つの許容場と仮想仕事の原理

節-3.1では，形を変える物体の幾何学的な関係式だけを 定義してまとめた。 そして，変形できる物体に力を加えたり歪めたりすると 形を変えることによって物体は抵抗するのであるが，節-3.2では 物体内部の抵抗「力」を定義し， 力学的な関係式だけをまとめた。そして次の節-3.3では， 物体の抵抗の仕方を表すのに節-3.1の 変形と節-3.2の抵抗力とを関係付ければいいことを説明した。 この節では，材料に依らず成り立つ重要な関係式を誘導しておく。

まず二つの許容場を定義する。変位ベクトル $\fat{u}\supersc{k}$が

$$\epsilon_{ij}\supersc{k}-\dfrac12 \left( \D{u_i\supersc{k}}{x_j}+ \D{u_j\supersc{k}}{x_i}\right)=0 \quad \mbox{in } V$$ (3.91)

を満足し，境界$S\subsc{k}$で

$$u_i\supersc{k}=\overline{u}_i=0 \quad \mbox{on } S\subsc{k}$$ (3.92)

を満足しているとき，この場を（零境界条件下^3.23の）運動学的許容場 と呼んでいる。ここで$V$は物体内体積部分を表し，$S\subsc{k}$は 幾何学的境界条件が与えられている表面部分を表している。 これに対し，応力テンソル $\fat{\sigma}\supersc{s}$が

$$\sum_{j=1}^3 \D{\sigma_{ji}\supersc{s}}{x_j}+X_i\supersc{s}=0 \quad\mbox{in } V$$ (3.93)

を満足し，境界$S\subsc{s}$で

$$\sum_{j=1}^3 n_j \sigma_{ji}\supersc{s}=\overline{F}_i\supersc{s} \quad \mbox{on } S\subsc{s}$$ (3.94)

を満足しているとき，この場を静力学的許容場 と呼んでいる。なお，$S\subsc{s}$は

$$S\subsc{s}\cup S\subsc{k}=S\equiv \partial V, \quad S\subsc{s}\cap S\subsc{k}=\emptyset$$

を満たすものとする。

式(3.93)に任意の運動学的許容場の $u_i\supersc{k}$を 乗じて，物体内で積分すると

$$\int_V \sum_{i=1}^3 \sum_{j=1}^3 u_i\supersc{k} \left\{\D{\sigma_{ji}\supersc{s}}{x_j}+X_i\supersc{s}\right\}\dint V=0$$

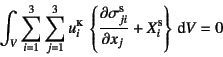
となる。これにGaussの発散定理を用いると

$$\int_S \sum_{i=1}^3 \sum_{j=1}^3 u_i\supersc{k} n_j \sig... ... +\int_V \sum_{i=1}^3 u_i\supersc{k} X_i\supersc{s} \dint V=0$$

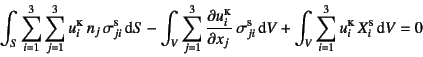
となるので，応力テンソル成分の対称性と ひずみ変位関係式(3.91)を用い， 境界条件式(3.92) (3.94)を考慮すると

$$\int_V \sum_{i=1}^3 \sum_{j=1}^3 \sigma_{ji}\supersc{s} \e... ...\sum_{i=1}^3 \overline{F}_i\supersc{s} u_i\supersc{k}\dint S$$ (3.95)

という関係式を得ることができる。この関係を仮想仕事の原理 と呼ぶ。同じ原理は，式(3.91)に 静力学的許容場の応力 $\sigma_{ji}\supersc{s}$を乗じた積分からも 得ることができる。

誘導過程から明らかなように，材料が 何であるかということとは無関係に，本来の仮想仕事の原理は成立する。 つまり，節-3.3で議論した構成則は 一切関係ない。また，運動学的許容場はつり合っている必要は無く， 静力学的許容場も変形の適合場に対応している必要も無い。 種々の境界値問題を解こうとしたとき，例えば力のつり合いを 満足するような解あるいはその近似解を得ることが容易な場合がある。 あるいは逆に，変形だけを近似的に推量できる場合もあるだろう。 そのときの全体の近似解を得るのに，この仮想仕事の原理と 応力ひずみ関係（材料の抵抗則・構成則）を さらに近似的に用いるというアプローチは可能かつ便利かもしれない。 具体的な使用例としては，章-5の 有限要素法や，章-9の 塑性解析等が挙げられる。

1. 式(3.91)から式(3.95)を求めてみよ。

最新版を正確に読むためには pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。