 |
最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
応力とひずみのことをある程度知っていて, 構造力学の勉強をしたい人は章-4から読めばいい。 そのようにしながら,もし途中でわからなくなったときに, この章に戻ってくるという読み方も可能である。 さて構造力学は変形できる物体の力学であるが,章-2では 変形そのものではなく,変形によって物体内部に生じる抵抗力つまり内力を導入し, 変形できる物体の抵抗の仕方を感じてもらった。 この章では変形そのものをきちんと定義し,その変形によって材料は どのような抵抗力を発揮することができるのか,という記述の仕方を 含めた連続体の力学の基礎を説明しよう。 なおこの章は, 微小変位・微小変形理論の枠組内の線形系の理屈だけを対象とする。
変形できる物体に外力等の外からの作用を与えた場合,
物体は移動し変形
するだろう。まず,その移動量を定義する。
簡単のために直交直線座標系で説明する。
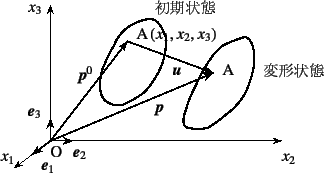
物体がまだ作用を受けていない状態を初期状態と呼び,
そのときの座標値の組![]() 3.1を,その座標位置に
存在する「点(粒子)」の
「名前」とする。即ち,図-3.1にあるように
物体中の点Aの初期の位置ベクトルを
3.1を,その座標位置に
存在する「点(粒子)」の
「名前」とする。即ち,図-3.1にあるように
物体中の点Aの初期の位置ベクトルを
とする。![]() は座標軸方向の単位基底ベクトルである。
さて,外からの作用を受けて
物体が変形し移動して図の右の方に示した位置に到達したとする。
そして物体点Aの,この状態での位置ベクトルが
は座標軸方向の単位基底ベクトルである。
さて,外からの作用を受けて
物体が変形し移動して図の右の方に示した位置に到達したとする。
そして物体点Aの,この状態での位置ベクトルが
になったものとする。
初期状態における位置ベクトルの座標成分![]() で
その物体中の点の名前を定義しているので,
変形した状態での位置ベクトルとその成分も
で
その物体中の点の名前を定義しているので,
変形した状態での位置ベクトルとその成分も![]() の
関数になる。
の
関数になる。
この変形前後の位置の差が物体中の任意点Aの移動量であることから
点Aの変位
ベクトルと呼び,それは
写真-3.2には正方形と円を書き込んだ
「のびのびサロンシップH」3.2の初期状態と,
左右方向に引張られた状態とが併せて示してある。
インクで印を付けることによってシートの特定な点に
「名前(式(3.1)の![]() という位置で定義した名前)」を
付けたことになっていて,その点(粒子)の動きを追跡している。
下の正方形と円が,変形した状態では
引張った方向に伸びてそれぞれが長方形と楕円になっている。
また,わずかだが引張った方向と直交する上下方向には縮んでいる。
一方上段の斜めにした正方形を見ると,変形後には角の直角が変化し,
それが伸び縮みと合わさって不等辺の平行四辺形になっている。
この簡単な実験から,物体の変形には少なくとも「伸び縮み」と
「角度変化」の2種類があることがわかる。
という位置で定義した名前)」を
付けたことになっていて,その点(粒子)の動きを追跡している。
下の正方形と円が,変形した状態では
引張った方向に伸びてそれぞれが長方形と楕円になっている。
また,わずかだが引張った方向と直交する上下方向には縮んでいる。
一方上段の斜めにした正方形を見ると,変形後には角の直角が変化し,
それが伸び縮みと合わさって不等辺の平行四辺形になっている。
この簡単な実験から,物体の変形には少なくとも「伸び縮み」と
「角度変化」の2種類があることがわかる。
簡単のために図-3.3に示したように![]() 軸
方向の物体点の変位で伸び
縮みを定義する。この
軸
方向の物体点の変位で伸び
縮みを定義する。この![]() 方向の伸びひずみ
成分を
方向の伸びひずみ
成分を![]() と
表記すると,元々
と
表記すると,元々![]() の長さを有していた微分要素は,
変形後には
の長さを有していた微分要素は,
変形後には
![]() の長さになる。
この1次元の図から
の長さになる。
この1次元の図から
という幾何学的関係にあるので,3次元物体中の任意点![]() での
伸びひずみ成分
での
伸びひずみ成分![]() を
を
で定義することができる。
やはり簡単のために図-3.4にあるように,
平面上の正方形が平行四辺形に変化した場合を考える。
元々軸と平行な辺でできていて直角であった
角が,![]() ,
, ![]() 軸とそれぞれ
軸とそれぞれ![]() ,
, ![]() だけ
図のように角変化が生じたとすると,左側の図から
だけ
図のように角変化が生じたとすると,左側の図から
と考えることができ,したがって同様に
と表現できることがわかる。 もちろん角度は非常に小さいものと仮定してある。
ここで注意しなければならないのは,それぞれの辺の
回転量に過ぎない![]() ,
, ![]() が必ずしも「変形」としての角変化だけを
表しているとは限らないということである。
例えば
が必ずしも「変形」としての角変化だけを
表しているとは限らないということである。
例えば![]() といった
特別な関係にある場合には,正方形は元々の直角は保持されたまま
回転するだけで,「変形=歪ゆがみ」の角度変化は生じていない。
そういった回転量をも
といった
特別な関係にある場合には,正方形は元々の直角は保持されたまま
回転するだけで,「変形=歪ゆがみ」の角度変化は生じていない。
そういった回転量をも![]() ,
, ![]() は含んでいることに
留意してこの図を眺めると,同じ図の右側で説明しているように
は含んでいることに
留意してこの図を眺めると,同じ図の右側で説明しているように
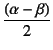 だけ
回転して破線で表した位置にくるが
だけ
回転して破線で表した位置にくるが
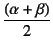 ずつ
お互いに反対方向に回転し,直角が崩れて変形し
ずつ
お互いに反対方向に回転し,直角が崩れて変形し
最終的な位置に落ち着くと考えた方がよさそうである。
つまり,回転角の中の一部分だけが
角度変化に相当するものと考えないといけない。
このことから,この![]() -
-![]() 面内での「変形」を伴う角度変化を
せん断ひずみ成分
面内での「変形」を伴う角度変化を
せん断ひずみ成分![]() と表記することにすると,それは
と表記することにすると,それは
で定義していいだろう。
式(3.5)を見ながら,
式(3.4)の伸びひずみ![]() を見ると,無理やり
を見ると,無理やり
とも書くことができることから,この![]() を
を![]() と
表記することにして
と
表記することにして![]() といっしょに
まとめると,任意点での変形状態を
といっしょに
まとめると,任意点での変形状態を
で定義した六つ(九つ)のひずみ
テンソル成分で
表すことができることに気付く。節-2.4.2の
不静定問題の式(![]() )が,この変形と変位の関係に相当する。
なお定義から明らかなように
)が,この変形と変位の関係に相当する。
なお定義から明らかなように
![]() で
あることから対称なテンソルと称され,九つのうち六つがある種独立した
ひずみ成分である。
で
あることから対称なテンソルと称され,九つのうち六つがある種独立した
ひずみ成分である。
テンソル
という言葉は,
大雑把には「ある種の物理的に意味のある量」を意味していると考えればいい。
スカラーやベクトルもテンソルの一種である。
それぞれ0階,1階のテンソルと呼ばれ,上述のひずみテンソルは2階の
テンソルと呼ばれる。
その表記には,成分を用いて式(3.6)のように
書く場合もあるが,直接表記と称してベクトルと同様に
![]() と
表記する場合もある。またその成分との関係を
ある種の表記上の規則を別途用意した上で
と
表記する場合もある。またその成分との関係を
ある種の表記上の規則を別途用意した上で
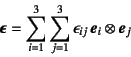
と書く場合(この文書ではほとんど用いない)や,行列表示で
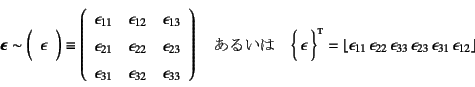
と表す場合もある。 列ベクトルの場合の成分の順番にはある合理性がある。
せん断ひずみを定義した際に見たように,物体の移動量には変形を
含んでいない部分がある。すなわち式(3.6)で
定義したひずみ成分を零にするような変位成分が存在する。
そういった変位を総称して剛体変位
と呼んでいる。
例えば図-3.5の
左の図は1本の棒がそのまま平行に移動しているだけなので,
変位ベクトルはいたるところ
![]() である。
したがって,式(3.6)に代入してもひずみ成分は
すべて零になる。このような変位成分を剛体並進変位
成分と呼ぶ。
右の図は同じく棒が原点の回りに回転しただけである。
したがって棒の中の任意点の変位成分は,
例えば微小回転で
である。
したがって,式(3.6)に代入してもひずみ成分は
すべて零になる。このような変位成分を剛体並進変位
成分と呼ぶ。
右の図は同じく棒が原点の回りに回転しただけである。
したがって棒の中の任意点の変位成分は,
例えば微小回転で
![]() としてもいい場合には
としてもいい場合には
等となるので,すなわち
となる。これもひずみの定義式(3.6)に代入すると, それはすべて零になる。 この変位成分を剛体回転変位 成分と呼ぶ。 このことから,外「形」が「変」わった(広義の変形)ように見えても, それはa)剛体(並進)変位とb)剛体回転との和である剛体変位 成分と,c)物体が外力に抵抗して「形」を「変」えた(狭義の) 変形成分あるいはゆがみ 成分との和になっていることがわかる。 今まで「変形」を正確には定義していなかったが,このc)の成分を「変形」と呼ぶ。 さらに,この狭義の「変形」は,i)伸び縮み成分とii)角度変化成分で できていることは,ここまでに示した通りである。 そういう意味から「変位」と「変形」も厳密に区別して用いる必要がある。
図-3.4でせん断ひずみを考えたときに,
任意の回転変形の中の
![]() を剛体回転成分と
解釈した。すなわち
を剛体回転成分と
解釈した。すなわち
は着目している点の回転成分であろう。
実際に上式(![]() )を代入すると
)を代入すると
![]() になる。
これを一般化し
になる。
これを一般化し
| (3.7) |
で微小回転
テンソル![]() の成分と
定義(添え字の順番が逆で正負が異なる定義も存在するので注意)する。
式(3.6)のひずみテンソル成分と併せて考えると
の成分と
定義(添え字の順番が逆で正負が異なる定義も存在するので注意)する。
式(3.6)のひずみテンソル成分と併せて考えると
となる。すなわち,変位勾配 テンソル成分(左辺)の対称成分(右辺第1項)がひずみテンソル成分であり, 反対称成分(右辺第2項)が微小回転テンソルになっていることがわかる。
再度写真-3.2を見直してみよう。 左の写真の上の正方形が水平な正方形に見えるように, そのページを反時計回りに若干回転させた状態にして,右の写真を見て欲しい。 このとき,上の正方形は平行四辺形になっているように見え, 下の正方形は角度変化が無いまま2方向に伸び縮みが生じただけに見える。 しかしこの実験は,一枚のシートを単純に左右に引張っただけなので, 上下の図形は本質的には完全に同じ変形状態にあるはずである。 にもかかわらず, 変形前には同じ形をしていた異なる向きを持つ二つの正方形の 変形を観察すると,それは それぞれ異なった図形になっている。 同じ変形状態なのに観測の仕方によって異なって見えてしまうことには 十分注意する必要がある。 すなわち,このシートの変形を表している 「ひずみテンソルそのものは一つの状態を表す物理量である」にもかかわらず, 見る向き即ち観測者が立脚している「座標系によって その成分は値が異なる」し,変形の性状も違って見える。 このことは,テンソル「成分」を安易に可視化したとしても力学的な本質が 見えるとは限らないことを示唆している。 特に膨大な数値解析結果を整理するときには,例えば汎用プログラムの ポストプロセサの利用では十分注意しなければならない。
この例を逆に考えると,どんな変形状態であっても写真の下の 正方形のような相直交する方向への単純な伸び縮みとして捉えることが できることもわかる。 このような,任意の変形を単純な伸び縮みとして捉えられる 向き(座標系)を見出したとき,その伸び縮みの方向をひずみの主方向と 呼んでいる。 また,その主方向のひずみ成分を主ひずみと 呼ぶ。具体的な求め方は,主応力に ついての節-3.2.6およびMohrの ひずみ円についての節-3.5.2 (3)で 説明する。写真-3.2の場合の主方向は, シートの2辺に沿った2方向である。
ひずみテンソルそのものは観測者に依らず, つまり成分を算定する座標系に依らず, ある一つの「変形」という物理量を表している。だから「テンソル」と 呼ばれている。逆に,写真でも見たように その成分は観測者の定義した座標系によって異なる値を持つ。 したがって「テンソル」と「テンソル成分」という言葉は注意深く 使い分ける必要があるが,この文書ではそのあたりはいい加減である。 ここでは,異なる座標系でのひずみテンソル成分間の関係を求めておく。 しつこいようだが,特に2次元3次元の連続体でテンソル「成分」を 解釈するときには,その座標系に物理的・材料学的必然性があるのかどうかを 注意深く考察しおく必要がある。 そうでもないときには,前節の主ひずみのような座標に依らない量を 解釈することを検討すべきである。
初期状態の任意の微分要素を取り出し,
その長さを![]() とすると,ピタゴラスの定理
から
とすると,ピタゴラスの定理
から
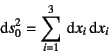
となる。これが変形後に![]() になったとすると,
式(3.2) (3.3)より
になったとすると,
式(3.2) (3.3)より
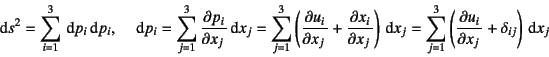
と書くことができる。ここに![]() はKroneckerのデルタ
と呼ばれ
はKroneckerのデルタ
と呼ばれ
という値を持つ記号(テンソル成分ではない)であり,
行列表示すると単位行列になる。![]() は
は![]() で微分すると1になるが
で微分すると1になるが![]() で
微分すると0になる。
そういったことを簡単に表すとき等に便利な記号で,この文書でもよく使われる。
式(3.8)の関係を上式に代入して少し演算すると,
線形部分だけの近似3.3の範囲で
で
微分すると0になる。
そういったことを簡単に表すとき等に便利な記号で,この文書でもよく使われる。
式(3.8)の関係を上式に代入して少し演算すると,
線形部分だけの近似3.3の範囲で
と書くことができる。つまり,ひずみテンソルの成分は上式のような 形で変形前後の微分要素の長さの差を表現している物理量になっている。 式(3.10)の演算は初学者には今は難しいとは思うが, 慣れると結構簡単なことをしているのがわかる。
ここで,異なる座標系![]() を考えた場合,式(3.10)の
左辺は座標系に依らず同じ値を持つスカラーなので,
新しい座標系でのひずみテンソル
成分を
を考えた場合,式(3.10)の
左辺は座標系に依らず同じ値を持つスカラーなので,
新しい座標系でのひずみテンソル
成分を
![]() と表記した場合に
と表記した場合に
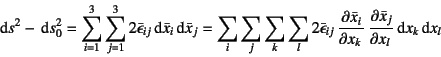
と記すことができる。ここで座標変換を
で定義すれば,上式右辺と式(3.10)の右辺とが等しい条件から,
ひずみテンソル成分同士の関係を
と得る。座標変換を行列表示すると,その正規直交性から
式(3.12)は
と行列表現もできる。Tの上付き
![]() は転置行列を表す。
この関係は,任意の2階のテンソル成分の座標変換則である。
は転置行列を表す。
この関係は,任意の2階のテンソル成分の座標変換則である。
伸びひずみ成分![]() 等は微分線要素の長さの伸び
変化を示していたから,ひずみが微小である限り,
体積ひずみ
は
等は微分線要素の長さの伸び
変化を示していたから,ひずみが微小である限り,
体積ひずみ
は
で定義できるはずだ。また,
ひずみテンソル成分からこの体積ひずみ成分を取り除いた
成分を偏差ひずみ
テンソル成分と呼び
で定義する。体積ひずみ成分を`3'で割ったものは,3方向の
伸びひずみの平均ひずみであり,また当然ではあるが,
偏差ひずみ
![]() は体積ひずみ成分を
持たない
は体積ひずみ成分を
持たない
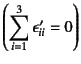 。
。
それぞれの物理的意味を理解するために,図に描き易い2次元空間で
考えてみよう。2次元の場合には,
体積ひずみ成分の代わりに面積ひずみ成分を考えればいいため,
少し定義を変えて
でいい。上付きの`(2)'で2次元であることを区別した。
例えば図-3.6の左の二つのように,2方向に
同じ伸び
![]() が生じたあと,2方向に同じ大きさで
異なる向き(伸びと縮み)の
が生じたあと,2方向に同じ大きさで
異なる向き(伸びと縮み)の
![]() が生じたとする。
すると,そのひずみ成分は
が生じたとする。
すると,そのひずみ成分は
となる。これから体積ひずみ成分![]() を求めると
を求めると
であり,偏差ひずみ成分
![]() は
は
となる。 つまり等方な変形が体積ひずみであり,2方向への 大きさの等しい伸び縮みが偏差ひずみである。 この偏差ひずみは少しわかり難いので,異なる座標系からこの変形全体を 眺め直してみよう。
まず,体積ひずみ成分に着目してみよう。行列表示すると
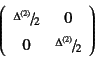
となるから,例えば45度だけ座標を時計回りに回転させてみよう。
式(3.13)の座標変換則を用いると
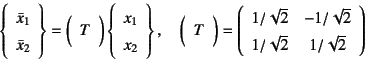
となるから,上の成分は回転させても
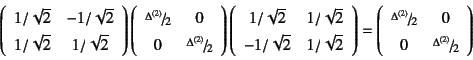
と無変化である。すなわち,体積(面積)ひずみはスカラー量であり, したがってどんな座標系から見ても 同じであるという,当然の結果を示すことができた。単位行列は どんなに回転しても単位行列のままであるのと同じことである。
では偏差ひずみ成分はどうだろう。同様に行列表示すると
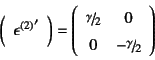
となる。つまり![]() 方向に伸びた分だけ
方向に伸びた分だけ![]() 方向には
逆に縮んでいる状態を表していた。体積ひずみの場合と
同様に45度だけ座標を時計回りに回転させると
方向には
逆に縮んでいる状態を表していた。体積ひずみの場合と
同様に45度だけ座標を時計回りに回転させると
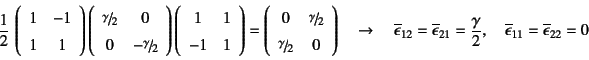
となる。すなわち,この45度回転した座標系
![]() で
偏差ひずみ成分を眺め直すと,
単純に
で
偏差ひずみ成分を眺め直すと,
単純に
![]() ずつの
角度変化(せん断ひずみ)だけしか生じていないことと
同じだということがわかる。
このことから,偏差ひずみ成分はせん断変形成分を表していると
考えていい。45度回転した座標系での
変形の様子を図-3.6の一番右に示した。
この例からも,任意の変形は体積ひずみとせん断ひずみの
和で表現されていると考えていいことがわかる。
また,座標系の選び方によって変形の様子が全く違って見えることも
実感できたと思う。
ずつの
角度変化(せん断ひずみ)だけしか生じていないことと
同じだということがわかる。
このことから,偏差ひずみ成分はせん断変形成分を表していると
考えていい。45度回転した座標系での
変形の様子を図-3.6の一番右に示した。
この例からも,任意の変形は体積ひずみとせん断ひずみの
和で表現されていると考えていいことがわかる。
また,座標系の選び方によって変形の様子が全く違って見えることも
実感できたと思う。
式(3.6)のひずみの定義式の左辺右辺を入れ替えて,ひずみ成分が与えられた場合の変位成分に対する
連立微分方程式だと考えると,三つの変位成分が
満足すべき六つの微分方程式と捉えることができる。
つまり,微分方程式の解の数より多い条件式が存在することになる。
一体どういうことだろう。
それは,六つのひずみ成分を自由に任意に与えたときには,
それに対する変位が存在しなかったり,唯一に求められなかったりすることを
意味する。
つまり,六つのひずみ成分の間には何らかの制約条件が存在しなければならない
ことになる。
このような制約条件をひずみの適合条件式
と呼んでいる。物理的説明は例えば文献[127]がわかり易いので,
ここでは結果のみを示す。
物体のある点Pでの変位とひずみとがわかっているとき,その近傍の点Qでの
変位は式(3.8)を用いて少し演算をすると
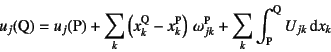
で与えられる。ここに
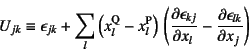
と置かれている。上の式の最後の積分はP![]() Qの積分路の選び方には依らずに
唯一に定まらなければならない。そうでないと点Qの状態が
複数存在してしまい,図-3.7の模式図[25]に
示したように,連続体中に穴が空いたり物質が重なったりしてしまうことになる。
この積分が経路に依存しない条件から
Qの積分路の選び方には依らずに
唯一に定まらなければならない。そうでないと点Qの状態が
複数存在してしまい,図-3.7の模式図[25]に
示したように,連続体中に穴が空いたり物質が重なったりしてしまうことになる。
この積分が経路に依存しない条件から
という関係(六つのうち三つが独立)を得る。
文献[82]にも数学的表現がなされているが,これが
ひずみの適合条件式である。特に2次元の場合には
となる。この式が正しいことは式(3.6)の2次元の 成分だけを左辺に代入すれば示すことができる。 このような適合条件を満足するひずみを適合ひずみ と呼ぶ。