 |
�ŐV�ł𐳊m�ɓǂޏꍇ�ɂ� pdf �t�@�C�� ���ǂ����B����� web �����̂��߂̊ȈՋ��łł��B
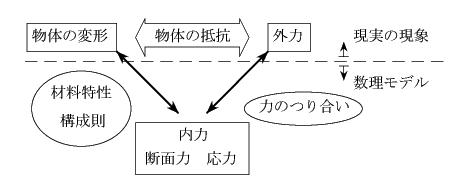
��-2�ł̓g���X�Ɨ����ɂ��āC ���́i��R�́j��f�ʗ͂Ƃ��ē����������C �����ł͂��̒�R�͂������ƍޗ��̕ό`�ƊW�t���āC�����I�� �Ƃ��납���`���������B �O�͂ɑ��ό`���Ē�R���镨�̂́C�O�߂̂Ђ��݂� ���̓����ɔ��������Ē�R���悤�Ƃ���B �Ⴆ�Ύ肪���M������ꍇ�C�ؓ��͔]����̐M���� �d�C�I���w�I�ɏ������ĕK�v�ȕ����������u���k�v������B ����ɂ���Ďw�ɋ����M�𗎂Ƃ��Ȃ������́u�́v�� ���M�ɗ^���Ă���B �m���Ɂu���q�ԗ́v�܂ł��ǂ�C���炩�̏��� ����ɑ�������̗͂��������Ē�R���Ă��邱�Ƃ͗����ł��邾�낤���C ���ۂ݂̂߂�ƁC ���̋ؓ��̎��k�ɑ�������u�ό`�v���u�O�́v�ɒ��ڒ�R ���Ă��邱�ƂɂȂ�B �������u�ό`�v�͖������ʂł���̂ɑ��C �u�O�́v�͗͂�[�����g�̎��������B ���������āC���̂悤�ɂ��݂��̎������قȂ���̓��m�� ��p����p�������Ē�R���Ă���悤�ɍl����͎̂v�l��̍���� ���낤�B���̂��ߏ�-2�ł́C���͂ƋȂ����[�����g�E ����f�͂Ƃ������f�ʗ͂����ĊO�͂ɒ�R�������B �����ł͑O�߂̕ό`�ƊW�t�����A���̂̓��͂��`����B �����Ő}-3.8�̂悤�ɁC �́i���邢�͋��͂∳�́j�̎������������u�����v �Ƃ�����R�́i���q�ԗ͂̕��ϒl�̂悤�Ȃ��́j��V������`��
�ƍl�������������Ղ����낤�B ���̐߂ł͂܂��A���̂ɐ�������́C �܂蕨�̂̒�R�͂���ʓI�ɒ�`���悤�B��-2�� �͎�Ƀg���X���ނ̉��́i��R�́j���C���z�I�Ɂi���̒��Łj���ނ� �ؒf���邱�Ƃɂ���ĉ����i�O�͂Ɠ����悤�Ɂj���čl��������C ����قǒ�R�Ȃ����̕����I�ȈӖ����z���E�����ł����Ǝv���B �����ň����A���̂̒��̉��͂́C���w�҂ɂ͓�����̂̑�\�ł���B �����䖝���Ă���������g��ŕ����ė~�����B ����Ȃ����Ƃ��́C�g���X�̎��͂̂��Ƃ��v���o���C �����͗������i�ނ�������Ȃ��B
���̓����̒�R�͂�������邽�߂ɁC�g���X���ނ�r���Őؒf�����̂�
���l�ɁC�܂��͕��̂�^����ɂ��Ă݂悤�B�}-3.9��
�悤�ɔC�ӂ̖@������![]() ���������\�ʂ����̂悤�Ȑؒf�ɂ����
������Ƃ��悤�B
���̓����\�ʂ̖ʐς�
���������\�ʂ����̂悤�Ȑؒf�ɂ����
������Ƃ��悤�B
���̓����\�ʂ̖ʐς�![]() �ŁC�����ɒ�R���邽�߂�
�������Ă���ł��낤�P�ʖʐϓ�����̒�R�̓x�N�g����
�ŁC�����ɒ�R���邽�߂�
�������Ă���ł��낤�P�ʖʐϓ�����̒�R�̓x�N�g����
![]() ��
����ƁC�O�͂Ƃ̂荇���͉E���̕���
��
����ƁC�O�͂Ƃ̂荇���͉E���̕���![]() �ɑ��Ă�
�ɑ��Ă�
�ƂȂ�͂����B![]() �͕��̖̂{���̕\�ʂɍ�p�����P�ʕ\�ʐϓ������
�O�͂ł���C
�͕��̖̂{���̕\�ʂɍ�p�����P�ʕ\�ʐϓ������
�O�͂ł���C![]() �͕��̓����ɍ�p����P�ʑ̐ϓ�����̊O�͂ł���B
���̒�R��
�͕��̓����ɍ�p����P�ʑ̐ϓ�����̊O�͂ł���B
���̒�R��
![]() �͏�-2��
�����������͓����f�ʗ��ɑ�������B
�������C�����ł͎����͒P�ʖʐϓ�����̗͂ƍl���Ă݂����̂��B
�����́u�\�ʁv�Ƃ������̂��C���̖̂{���̕\�ʂł͂Ȃ��C
���z�I�Ɂi���̒��Łj���̂��I�ɐؒf���Č��ꂽ�\�ʂ��w�����Ƃɂ�
�\�����ӂ���K�v������B
�͏�-2��
�����������͓����f�ʗ��ɑ�������B
�������C�����ł͎����͒P�ʖʐϓ�����̗͂ƍl���Ă݂����̂��B
�����́u�\�ʁv�Ƃ������̂��C���̖̂{���̕\�ʂł͂Ȃ��C
���z�I�Ɂi���̒��Łj���̂��I�ɐؒf���Č��ꂽ�\�ʂ��w�����Ƃɂ�
�\�����ӂ���K�v������B
��ł͏�-2�̒f�ʗ͂�
��ʉ����邽�߂ɕ��̂����傫�Ȗʂ��l�������C
�A���̒��̎��ۂ̓��͕͂��̓��̏ꏊ![]() �̊��ɂȂ邽�߁C
���̓��̂���Ǐ��I�ȓ_�ߖT�ɂ����Ĕ����ʐ�
�̊��ɂȂ邽�߁C
���̓��̂���Ǐ��I�ȓ_�ߖT�ɂ����Ĕ����ʐ�![]() ���l����K�v������B
�����ŁC�}-3.9�̐ؒf�ʏ�̓�ӏ���
�E����
���l����K�v������B
�����ŁC�}-3.9�̐ؒf�ʏ�̓�ӏ���
�E����![]() �̒��ɎO�ӏ��Ꭶ�����悤�ɁC����_�ߖT��
���������\�ʗv�f
�̒��ɎO�ӏ��Ꭶ�����悤�ɁC����_�ߖT��
���������\�ʗv�f![]() �ɐ������Ǐ��I�ȓ���
�ɐ������Ǐ��I�ȓ���
![]() ��
���ڂ��Ă݂悤�B���̓���
��
���ڂ��Ă݂悤�B���̓���
![]() ���\�ʗ�
�ƌĂ��B���̗̓x�N�g�����\�ʗ̓x�N�g��
3.5�ƌĂԂ��Ƃ�����B
�����͈��͂Ɠ����ŒP�ʖʐϓ�����̗͂ł���B
��œ��������f�ʗ͂ɑ����������
���\�ʗ�
�ƌĂ��B���̗̓x�N�g�����\�ʗ̓x�N�g��
3.5�ƌĂԂ��Ƃ�����B
�����͈��͂Ɠ����ŒP�ʖʐϓ�����̗͂ł���B
��œ��������f�ʗ͂ɑ����������
![]() �́C
�^����ɂ����f��
�́C
�^����ɂ����f��![]() �̕��ϓI�ȕ\�ʗ�
�̕��ϓI�ȕ\�ʗ�
�ł���B
���̂悤�ɁC����_�Œ�`�����\�ʗ͂̓x�N�g���Ȃ̂�
�������O�̍��W���������͂������C
���̓����_���܂ޓ����\�ʂ̌���![]() ���ς��ƁC���̐����̒l��
����Ă��邾�낤�B�܂�C�\�ʗ͂ɂ́C
�����\�ʂ̌����̏����܂߂ĕ\�����Ȃ���Ȃ�Ȃ��B
�����Ő}-3.10�ɂ�
�ȒP�̂��߂�2�����ł̏��������B
���̐}��
���ς��ƁC���̐����̒l��
����Ă��邾�낤�B�܂�C�\�ʗ͂ɂ́C
�����\�ʂ̌����̏����܂߂ĕ\�����Ȃ���Ȃ�Ȃ��B
�����Ő}-3.10�ɂ�
�ȒP�̂��߂�2�����ł̏��������B
���̐}��![]() �͕��̓����̔����ʐϗv�f�ł���B
���̒P�ʖ@���x�N�g����
�͕��̓����̔����ʐϗv�f�ł���B
���̒P�ʖ@���x�N�g����![]() �ł������̓�����
�C�ӂ̈ʒu
�ł������̓�����
�C�ӂ̈ʒu![]() �ɒ�`���������\�ʗv�f��
�\�ʗ�
�ɒ�`���������\�ʗv�f��
�\�ʗ�
![]() ���������Ă���ɑ��C
�}�������悤��
���������Ă���ɑ��C
�}�������悤��
![]() �ŕ\���������̍��W������������
�P�ʖʐϓ�����̗͐������`����B������̗͂��P�ʖʐϓ�����̗͂�
���邱�Ƃɒ��ӂ���ƁC���ꂼ��̍��W�������̗͂̂荇����
�ŕ\���������̍��W������������
�P�ʖʐϓ�����̗͐������`����B������̗͂��P�ʖʐϓ�����̗͂�
���邱�Ƃɒ��ӂ���ƁC���ꂼ��̍��W�������̗͂̂荇����
�ƂȂ邩��C���ǁC�\�ʗ̓x�N�g���̊e���������ꂼ��ʂ̕�����
�ˑ������O�̐���![]() �������ƂɂȂ�
�������ƂɂȂ�
�܂�
��![]() ���`���邱�Ƃɂ��悤�B����
���`���邱�Ƃɂ��悤�B����![]() ������
�e���\���ƌĂсC��̂��ꂼ��̐��������̓e���\�������ƌĂԁB3�����̏ꍇ�ɂ�
������
�e���\���ƌĂсC��̂��ꂼ��̐��������̓e���\�������ƌĂԁB3�����̏ꍇ�ɂ�
�����̓e���\���̒�`���ł���B���̒�`����Cauchy�̒藝
�ƌĂԂ��Ƃ�����B���̎�(3.19)�ڕ\�L���邢�͍s��\�L��
�ƍl���C
���̓e���\�����x�N�g���Ԃ̎ʑ��Ƃ��Ē�`����l������悤���B
���̂悤�ɉ���3.6��
����ʂ̊O�����@���x�N�g���Ɗ֘A������
��`����邽�߁C���̐��̌����͓����\�ʂ̌����Ɉˑ����Ă���B
����ɂ��Ă͎��߂Œ�`����B���͐���![]() �̂����C
�����\�ʂ̖@�������i
�̂����C
�����\�ʂ̖@�������i![]() �j������������
�ƌĂсC�ڐ������i
�j������������
�ƌĂсC�ڐ������i![]() �j����������f����
�ƌĂԁB
�j����������f����
�ƌĂԁB
�����܂ł̐}-3.10�⎮(3.18)��
�p�������̓e���\���̐����̒�`�C�܂�Y�����̋K���ɂ��ẮC
�܂����m�ɂ��Ă��Ȃ������B
����͐}-3.11�̂悤�ɂ���̂��ʗ�ł���B
�@��![]() �����ʂɍ�p����\�ʗ̓x�N�g����
�����ʂɍ�p����\�ʗ̓x�N�g����
![]() ��
��`�����̂ŁC���W�̒P�ʃx�N�g��������@���Ƃ�������\�ʗv�f��
���̓����ɐݒ肵���ꍇ�C�Ⴆ��
�}�������悤�ɁC
��
��`�����̂ŁC���W�̒P�ʃx�N�g��������@���Ƃ�������\�ʗv�f��
���̓����ɐݒ肵���ꍇ�C�Ⴆ��
�}�������悤�ɁC![]() �������邢��
�������邢��![]() ������@���Ƃ���
�ʂɐ������\�ʗ̓x�N�g�����C���ꂼ��
������@���Ƃ���
�ʂɐ������\�ʗ̓x�N�g�����C���ꂼ��![]() ���邢��
���邢��![]() ��
�\�����Ƃɂ���B
�����ŁC���̃x�N�g���̊e���W����������
��
�\�����Ƃɂ���B
�����ŁC���̃x�N�g���̊e���W����������
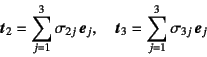
�̂悤�ɕ������āC���̐�����![]() ���邢��
���邢��![]() (
(![]() , 2, 3)�ƒ�`���邱�Ƃɂ���B���Ȃ킿�C��ʓI�ɂ�
, 2, 3)�ƒ�`���邱�Ƃɂ���B���Ȃ킿�C��ʓI�ɂ�
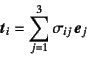 |
(3.20) |
�ƂȂ�B
����������![]() �̓Y�����̂����C�O�̓Y����
�̓Y�����̂����C�O�̓Y����![]() ���\�ʗ̓x�N�g����
��`���镨�̓����ʂ̖@���������C
������̓Y����
���\�ʗ̓x�N�g����
��`���镨�̓����ʂ̖@���������C
������̓Y����![]() �����͐������͂̌�����\���Ă���3.7���Ƃɒ��ӂ��ׂ��ł���B
��������q�̂悤�ɁC�����̏ꍇ���̓e���\���͑Ώ̃e���\���Ȃ̂ŁC
�����ɖ��L�����悤�ȓY�����̋�ʂ��d�v�ɂȂ邱�Ƃ͖������C��
�╪�z�O�̓��[�����g�����݂���ꍇ[51]�C
���邢�͑�ό`����ΏۂƂ���ꍇ�ɂ́C
���̋�ʂ��d�v�ɂȂ邱�Ƃ�����̂Œ��ӂ���B
�����͐������͂̌�����\���Ă���3.7���Ƃɒ��ӂ��ׂ��ł���B
��������q�̂悤�ɁC�����̏ꍇ���̓e���\���͑Ώ̃e���\���Ȃ̂ŁC
�����ɖ��L�����悤�ȓY�����̋�ʂ��d�v�ɂȂ邱�Ƃ͖������C��
�╪�z�O�̓��[�����g�����݂���ꍇ[51]�C
���邢�͑�ό`����ΏۂƂ���ꍇ�ɂ́C
���̋�ʂ��d�v�ɂȂ邱�Ƃ�����̂Œ��ӂ���B
�Ƃ���ŃX�g���X �i���́j�Ƃ������t�ɂ��āC ����[88]�ɖʔ����L�q������B ��������p����Ǝ��̂悤�Ɂi�����c�����j�Ȃ�B
�@�܂��A�X�g���X�Ƃ͉����B���t�{���̈Ӗ��Ƃ��ẮA�h���A �������͌ł����߂��邱�Ƃł���܂��ˁB��������
�@�͊w�̂ق��ł́A���̂ɊO����͂�������ꂽ���A���̓����� ������c�䂪�݂��X�g���X�ƌĂ�ł���܂��ˁB
�@���̓����ɐ�����c�݂Ƃ����Ӗ����A�J�i�_�̕a���w�҃n���X�E�Z���G ����w�ɓ����������܂����B���ꂪ�X�g���X�w���ł���܂��āA���㗪��
����͊m���ɊԈ�����L�q�ł���B������X�ł���w�p��� ���Ắu�X�g���X�v�̊��o�I�F���́C�g�̂̒��̉��炩�́i���_�I �Ȃ��̂��܂߂āj�䂪�݂ɂȂ��ĂȂ����낤���B �ؓ��̓����}-3.8������ƁC �����������炻�ꂪ�{����������Ȃ��B ���ۂɂ͕ό`��Ȃ����͂ɂ͈Ӗ��������C ���Ԃ��čl����Ɓw�u�́v�̎������������u�ό`�i�c�䂪�݁j�v�x�� ���͂̐^�`�Ȃ̂�������Ȃ��B���B�b�x��B
�㎮(3.19)�Œ�`���ꂽ���̓����̉��͐����́C
�O�͂���p���ĐÎ~������Ԃ̕��̓��̂��ׂẮu�_�v�ɂ����Ă�
�荇����Ԃɂ���͂����B
�����ŊȒP�̂��߂ɍēx2�����ŕ`�����}-3.12��
�p���āC���̂荇������U������B
�O�߂Œ�`�����悤�ɉ��͍͂�p�ʊO�������������ł��������߁C
���̐}�̂悤�ɁC�ʂ̊O�����@�������W�̐������������Ă����
�i���̖�
�j�ł͍��W�̐����������𐳂̉��͐����Ƃ���B
�t�����̖�
�ł͍��W�̕����������𐳂̉��͐����ƒ�`����B
�u�\�ʁv���w�肳��ď��߂Ē�`�ł���͂��̉��͂�
�C�ӂ̕����u�_�v�i�ʐς������j�ł荇���Ƃ����Ƃ��낪�C
�A���̗͊w�𗝉������ł̎��̓�ł��낤���C
���̐}�̂悤�ɏ������̈���l�������Ƃ�![]() ���ɂ���Ɍ���
�l����Ƃ����C
�������f����̂荇���ł��邱�Ƃ𗝉����ė~�����B
���ɂ���Ɍ���
�l����Ƃ����C
�������f����̂荇���ł��邱�Ƃ𗝉����ė~�����B
���͂��P�ʖʐϓ�����̗͂ł��邱�Ƃ�O���ɒu���āC����
�}�̉��s�����̌�����1���ƍl����C�Ⴆ��![]() ������
�͂̂荇����
������
�͂̂荇����
�ł��邱�Ƃ���C�荇������
�ƂȂ�B������![]() �͑̐ϗ�
�x�N�g��
�͑̐ϗ�
�x�N�g��![]() ��
��![]() ���������ŁC
�P�ʑ̐ϓ�����ɍ�p����͂̎����������C�Ⴆ�Ύ��d�̂悤��
���̂����f�����������̂ł���B
���������ŁC
�P�ʑ̐ϓ�����ɍ�p����͂̎����������C�Ⴆ�Ύ��d�̂悤��
���̂����f�����������̂ł���B![]() ���������l�ɗU���ł��邱�Ƃ���C����
���������l�ɗU���ł��邱�Ƃ���C����
��2�����̉��͐����̂荇�����ɂȂ�B3�����̏ꍇ��
�����̂荇���� �ł���B�����̉��͐����̓Y�����̏��Ԃɂ͒��ӂ��ė~�����B �����̕����ł́C���̏��Ԃ��t�ɂȂ��Ă��邪�C����͎��̃��[�����g�� �荇������������ꍇ�ɂ̂ݐ������C���̂Ƃ��̒��ڕ\�L�͂������� �ʓ|�ɂȂ�B
����C�}-3.12�̓_A���̃��[�����g�� �荇�����l�����
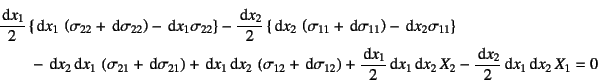
�ƂȂ邱�Ƃ���C�ӁX
![]() �ŏ������
��1������
�ŏ������
��1������
![]() �ƂȂ�B
���Ȃ킿3�����ł̃��[�����g�̂荇����
��
�ƂȂ�B
���Ȃ킿3�����ł̃��[�����g�̂荇����
��
�ł���B��(3.6)�Œ�`���ꂽ�Ђ��݃e���\�������� ���̒�`����Ώ̂ɂȂ��Ă������C���̓e���\�������̓��[�����g�� �荇������Ώ̂ƂȂ��Ă���B�������C �傫�ȕό`�������ꍇ�ɗp���鉞�̓e���\���ɂ� �Ώ̂ɂȂ�Ȃ����́i��1 Piola-Kirchhoff����[127]�j�����݂��邵�C�� �╪�z�O�̓��[�����g�����݂���ꍇ[51]�ɂ� ��(3.23)�͐������Ȃ��B
�}-3.9�̂悤�ȕ��̂̂荇����Ԃ���͂���ꍇ�C
���̕��̂̊O���\�ʂł͋��E������^����K�v������B
����ɂ͎��2��ނ̏���������B
��͂��̕\�ʂ̉^�����K�肷����̂ł���C
������͂��̕\�ʂɍ�p���Ă���O�͂�^������̂ł���B
�O�҂͕\�ʂł̕ψʂ�^������������ψʂ̋��E����
�ƌĂ�3.8��C��҂͕\�ʋߖT�ŕ\��3.9�O��
�x�N�g��![]() �Ɖ��͂�
�荇���悤�ɂ�����������͂̋��E����
�ƌĂ�3.10��B��̓I�Ɏ��ŕ\������ƁC�C�ӂ̕\�ʂ�
�Ɖ��͂�
�荇���悤�ɂ�����������͂̋��E����
�ƌĂ�3.10��B��̓I�Ɏ��ŕ\������ƁC�C�ӂ̕\�ʂ�
(3.24)
�̂����ꂩ���^�����邱�ƂɂȂ�B������![]() ��
���E�ŗ^����ψʐ����̒l�ł���B�܂���(3.24b)�́C
��(3.19)���O���\�ʂŗ��Ă����̂ŁC
����
��
���E�ŗ^����ψʐ����̒l�ł���B�܂���(3.24b)�́C
��(3.19)���O���\�ʂŗ��Ă����̂ŁC
����![]() �͊O���\�ʂ̊O�����@���P�ʃx�N�g���ł���B
�͊O���\�ʂ̊O�����@���P�ʃx�N�g���ł���B
��(3.24)�̓����{�I�ȋ��E�����ł��邪�C
�����g�ݍ��킹�����������蓾��B
�������3��̋��E����
�ƌĂ�3.11�邱�Ƃ�����C�e���I�Ɏx������Ă���\�ʂł̏��������̑�\�ł���B
��̓I�ɂ́C�Ⴆ�Ζ��C�̖����e���x���ǂ̒P�ʖʐϓ������
�@������![]() �̔��̓o�l�W����
�̔��̓o�l�W����![]() �Ƃ����Ƃ��C���̏�����
�Ƃ����Ƃ��C���̏�����
���邢��
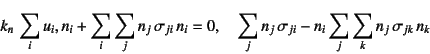
�ƕ\�����Ƃ��ł���B
������![]() �͕\�ʂ̊O�����@��
�͕\�ʂ̊O�����@��![]() �����̕ψʐ����ł���C
�����̕ψʐ����ł���C![]() ��
�\�ʗ�
��
�\�ʗ�![]() �̊O�����@�����������ł���B�܂�
�̊O�����@�����������ł���B�܂�![]() �͐ڐ����������ɂȂ�B
�͐ڐ����������ɂȂ�B
���镨�̂̕\��![]() �ɒP�ʕ\�ʓ�����
�ɒP�ʕ\�ʓ�����![]() �Ƃ����O�͕\�ʗ́i���͂�
��O�͂��܂ށj����p���C
���̓���
�Ƃ����O�͕\�ʗ́i���͂�
��O�͂��܂ށj����p���C
���̓���![]() �̒P�ʑ̐ϓ�����̕��z�O�͂�
�̒P�ʑ̐ϓ�����̕��z�O�͂�![]() �ł���ꍇ�C
���̑S�̂̊O�͓��m�������I���荇������
�ł���ꍇ�C
���̑S�̂̊O�͓��m�������I���荇������
�ł���B���̑�1����![]() �ɗ͂̋��E������(3.24b)���������
�ɗ͂̋��E������(3.24b)���������
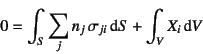
�ƂȂ�B��1���ɔC�ӂ̃e���\������![]() ��
����Gauss�̔��U�藝
��
����Gauss�̔��U�藝
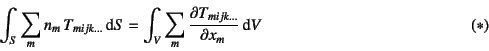
��p����ƁC�㎮��
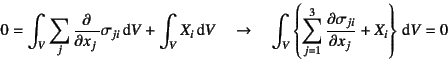
�ƂȂ�C��ϕ����͉��͂̂荇����(3.22)�Ɉ�v����B
�܂�C��(3.22)�͕���![]() �̒���
�C�ӂ̓_
�̒���
�C�ӂ̓_![]() �ɂ������Ǐ��I���������ׂ��荇�����ł��邱�Ƃ�
�킩��B
�ɂ������Ǐ��I���������ׂ��荇�����ł��邱�Ƃ�
�킩��B
���l�ɁC�S�O�͂̃��[�����g�������I���荇����
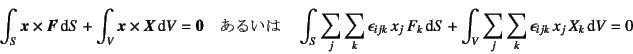
�ƂȂ�B������
![]() �����L��
�i�e���\�������ł͂Ȃ��j�ƌĂ�
�����L��
�i�e���\�������ł͂Ȃ��j�ƌĂ�
�Ƃ����l�����B���u��
�Ƃ́C(![]() )�̑g��(123) (231)
(312)�̏��̑g�̂����ꂩ�̏ꍇ�ŁC��u��
��(321) (213)
(132)�̏��̑g�̂����ꂩ�̏ꍇ�ł���B
����̓x�N�g���̊O�ς𐬕��\������ꍇ�ɕ֗��ȋL���ł���B
)�̑g��(123) (231)
(312)�̏��̑g�̂����ꂩ�̏ꍇ�ŁC��u��
��(321) (213)
(132)�̏��̑g�̂����ꂩ�̏ꍇ�ł���B
����̓x�N�g���̊O�ς𐬕��\������ꍇ�ɕ֗��ȋL���ł���B
���āC�㎮��1����![]() �ɍēx�͂̋��E������(3.24b)���������
�ɍēx�͂̋��E������(3.24b)���������
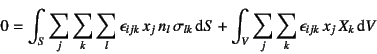
�ƂȂ�̂ŁC�܂���(![]() )��Gauss�̔��U�藝��
��1���ɓK�p�����
)��Gauss�̔��U�藝��
��1���ɓK�p�����
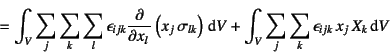
���Ȃ킿
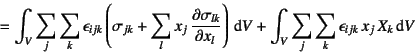
�ƂȂ�B���̑�1���̔�ϕ����̑�2����
�荇����(3.22)��������ƁC����
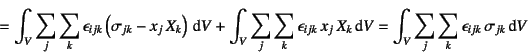
�ƂȂ�B�����
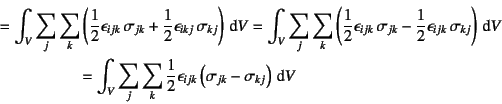
�ƂȂ邱�Ƃ���C���͂ŕ\�������[�����g���Ǐ��I���荇�� ��(3.23)���C��ϕ����ɓ���B
�Ђ��݂̏ꍇ�Ɍ����ʐ^-3.2����́C
�Ђ��݃e���\���ɂ͎����������C�C�ӂ̂Ђ��ݏ�Ԃ�
���̎�����ւ̎O�̐L�яk�ݐ��������ŕ\���ł��邱�Ƃ��킩���Ă����B
����Ȃ�Γ��l�ɁC
���̓e���\���ɂ�����������肻�����B�܂�C��������̓����\�ʂɂ�
����f���͐������������Ă��炸�C���̖ʂ̖@�������݂̂̉���
�����������݂��Ȃ��ʂ����肻�����B���̂悤�Ȗʂ̖@��
���������͂̎����
�ƌĂ�ł���B
������̒P�ʃx�N�g����
![]() �Ƃ����Ƃ��C
���̖ʂ̕\�ʗ͂͂��̖@�������ƕ��s�ɂȂ�͂�������C��(3.19)���
�Ƃ����Ƃ��C
���̖ʂ̕\�ʗ͂͂��̖@�������ƕ��s�ɂȂ�͂�������C��(3.19)���
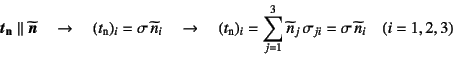
�Ƃ����W�ɂ���͂����B������![]() �͕��s���Ӗ�����L���ł���C
�X�J���[�W��
�͕��s���Ӗ�����L���ł���C
�X�J���[�W��![]() �͂��̎�����̉��͐����̑傫�����剞��
�ƌĂ��B���Ȃ킿�C�㎮����
�͂��̎�����̉��͐����̑傫�����剞��
�ƌĂ��B���Ȃ킿�C�㎮����
���邢��
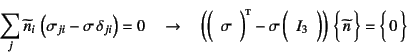
���������
![]() �Ǝ剞��
�Ǝ剞��![]() �Ƃ����݂���B
������
�Ƃ����݂���B
������![]() ��3
��3![]() 3�̒P�ʍs��ł���B
��(3.23)�̃��[�����g�̂荇�����C���͂�
�s��\���������̂͑Ώ̍s��ɂȂ邱�Ƃ���C��̎��̈�ԉE�̍s��\������
3�̒P�ʍs��ł���B
��(3.23)�̃��[�����g�̂荇�����C���͂�
�s��\���������̂͑Ώ̍s��ɂȂ邱�Ƃ���C��̎��̈�ԉE�̍s��\������
�Ə����Ă������B
��(3.27)�͍s��![]() �̌ŗL�l��
�̌ŗL�l��![]() ��
�����Ƃ��̕W���I�ȌŗL�l�����`�����Ă���C
���̌ŗL�x�N�g��������������ɂȂ��Ă���B���������Ď剞�͂�
��
�����Ƃ��̕W���I�ȌŗL�l�����`�����Ă���C
���̌ŗL�x�N�g��������������ɂȂ��Ă���B���������Ď剞�͂�
�Ō��肳��C���ʂ��㎮(3.27)�ɑ����������
�����
![]() ��
���߂邱�Ƃ��ł���B
��
���߂邱�Ƃ��ł���B![]() ���Ώ̍s��Ȃ̂ŁC
��ʂɎ剞�͎͂����ŎO���݂���B
���Ώ̍s��Ȃ̂ŁC
��ʂɎ剞�͎͂����ŎO���݂���B
�Ⴆ��2�����Ōv�Z���Ă݂悤�B��(3.27)��
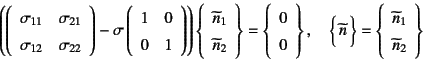
�ƂȂ�C��(3.28)�̍ŏI�I�Ȍ`
����̎剞��![]() ,
,
![]() �����肷��B
�ʏ�C���̑傫�������珇�Ԃ�I, II�Ƃ���B�����
�㎮�ɑ����������
�����肷��B
�ʏ�C���̑傫�������珇�Ԃ�I, II�Ƃ���B�����
�㎮�ɑ����������
�Ƃ����W�ɂȂ�̂ŁC���̂����ꂩ�̎���![]() ��
�剞��
��
�剞��![]() ���邢��
���邢��
![]() ��������C
���ꂼ��̎����
��������C
���ꂼ��̎����
![]() ,
,
![]() �̍��W���������߂邱�Ƃ��ł���B
�����ł�
�̍��W���������߂邱�Ƃ��ł���B
�����ł�
![]() ��
�P�ʃx�N�g���Ƃ��Ă���̂ŁC�B��Ɍ��肷�邱�Ƃ��ł���B
��
�P�ʃx�N�g���Ƃ��Ă���̂ŁC�B��Ɍ��肷�邱�Ƃ��ł���B
�����剞�͂����肷�� ��(3.28)���d�������ꍇ�C���Ȃ��Ƃ�2������ �剞�͂��������Ȃ�C������͗B��ɂ͌���ł��Ȃ��Ȃ�B2������ �ꍇ�̂Ђ��݂ōl�@����Ƃ킩��Ղ����C���̂悤�� �ꍇ�ɂ͎ʐ^-3.2�̕ό`��̑ȉ~���~�̂܂܂� �Ȃ��Ă��邱�Ƃɑ�������B����͂��ׂĂ̕����Ɉ�l�ɐL�� ���邢�͏k�݂������Ă����Ԃɓ������B�����ĉ~�̏ꍇ�ɂ́C�ȉ~�̒��Z���� ��������������C�ӂ́i�������������Ȃ��Ă������j������ ��邱�Ƃ��ł��邱�Ƃ���C���̎�����͗B��ɂ͌��肳��Ȃ��킯�ł���B ���͂̏ꍇ�����l�ŁC�d���̏ꍇ�ɂ́C����Ɋ֘A�����ʓ��Ɉ�l�� �����肩���k�������Ă��邽�߁C���ׂĂ̕�����������̌��ɂȂ�C ���������Ď������B��ɂ͌���ł��Ȃ��B
���āC�قȂ��̎剞�͂Ǝ�����͗Ⴆ�s��\���ł͂��ꂼ��
�����Ă���B���̑�1����
������
![]() ���C
��2���ɍ�����
���C
��2���ɍ�����
![]() ��
�悶��ƁC���ꂼ��
��
�悶��ƁC���ꂼ��
�ƂȂ�B����̓X�J���[�Ȃ̂ŁC��2���̓]�u�͍s�Z�̋K����p�����
�Ƃ��������Ƃ��ł��邩��C������̍��̎����炱�̎���ӁX���������C
���͂̑Ώ̐��𗘗p����ƍ��ӂ͗�ɂȂ�B����Ă��̉E�ӂ���
�Ƃ����W��B
���������āC�剞�͓��m���قȂ�
![]() �̏ꍇ�ɂ�
�̏ꍇ�ɂ�
�����_�t������B�܂�قȂ��������m�͒������Ă���B3������
�̈�ʓI�ȕ\��������Ȃ�C�قȂ�剞�͂ɑΉ������������m��
�ƂȂ肨�݂��ɒ������Ă���B�������C��̎剞�͂������ꍇ�ɂ́C �������B��ɒ�߂邱�Ƃ͂ł��Ȃ����C������������ɑI�Ԃ��Ƃ͂ł��邾�낤�B
��(3.27)�������[���ƒ��߂Ă���ƁC���̂悤��
���͍s���\���ł��邱�Ƃ��킩��i�l�͂����������̂ł��B
��1���҂͋t�Z�B���j�B
�e���\�����X�y�N�g���\��
�ƌĂ�邱�Ƃ�����B
�܂�C��(3.32)��
���ӂ�
![]() ���悶���
���悶���
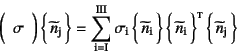
�ƂȂ���̂́C�E�ӂ̉E�[�̓��ς͎�(3.31)��
���𐫂��l�����
![]() �̂Ƃ��ȊO�͗�ɂȂ邽�߁C���Ǐ㎮��
�̂Ƃ��ȊO�͗�ɂȂ邽�߁C���Ǐ㎮��
�ƂȂ�C��(3.27)�ɋA������B�Ӗ����l���Ă݂悤�B
���̓e���\���͘Z�̍��W�����̑g�ŕ\�����Ƃ��ł��邪�C
���̘Z�̒l�͍��W�n�̂Ƃ���ɂ���Ĉ���Ă���B
�������㎮�̂悤�ɁC�O�̌ŗL�l�Ƃ��ꂼ��ɑΉ�����O��
������x�N�g���i�O�̐������Ɨ������P�ʒ����x�N�g���̑g�j��
�̑g�ݍ��킹�ł��\���ł���Ƃ������Ƃ́C
���W�n�Ƃ͑S�����W�̘Z�̗ʂʼn��̓e���\��������ł��Ă���
���Ƃ������Ă���B���ꂪ�u�e���\���v�ł���R���ł͂Ȃ����낤���B
���邢�͎�(3.32)���C�O�̊��̃e���\��
��
![]() ��
���̓e���\���������Ƃ��̂��ꂼ��̐������剞�͂ł����
����l������悤���B
���ɍޗ��̒�R���i���͂Ђ��݊W�j���l����ꍇ�ɂ́C����͖{���I�ɍ��W�n�Ƃ�
���W�łȂ���Ȃ�Ȃ�����C�剞�͂��Ђ��݁i��L�сj��p���邱�Ƃ�����B
��
���̓e���\���������Ƃ��̂��ꂼ��̐������剞�͂ł����
����l������悤���B
���ɍޗ��̒�R���i���͂Ђ��݊W�j���l����ꍇ�ɂ́C����͖{���I�ɍ��W�n�Ƃ�
���W�łȂ���Ȃ�Ȃ�����C�剞�͂��Ђ��݁i��L�сj��p���邱�Ƃ�����B
��Ō����悤�ɁC�Ђ��݃e���\���Ɠ��l�C
���̓e���\�������͗p������W�̂Ƃ���Ɉˑ�����
�l�͕ω����Ă��܂��B�������C���鉞�͏�Ԃɑ��āC���̎剞�͂�
���̕��̓_�ɂ������R�͂̕����I�ȓ����̈�ł����āC
���W�̂Ƃ���Ƃ͑S���W�̖����l�ƌ����������Ă���B
���������āC�㎮(3.29)��2����������
���ƌW���̊W���瓾�邱�Ƃ��ł���
| (3.33) |
�Œ�`������̗ʂ́C���W�n�Ɉˑ����Ȃ��ʂɂȂ�B ���̂悤�ȗʂ��s�ϗ� �ƌĂ�ł���B
3�����̈�ʓI�ȕ\���������ƁC�剞�͂����肷�鎮��
| (3.34) |
�Ə����C���ꂼ��
�����͂̑�1�`��3�s�ϗ� �ł���B��1�s�ϗʂ͍s��\�������Ƃ��̐� �ɑ�������B ����ɑΉ������āC�Ђ��݂̕s�ϗʂ���`�ł���B ���̂悤�ȕs�ϗʂ��ޗ��̒�R���i���͂Ђ��݊W�j��\������̂� �K���Ă���C���ۂɑY���̊�b���ŗp�����Ă���B
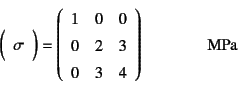
���̓e���\�����Ђ��݃e���\���Ɠ��l�C������Ԃł����Ă��C
�قȂ���W�n�ɑ��Ă͈قȂ�l�����̐����͎��B
��(3.11)�̍��W�ϊ��s��̒�`����
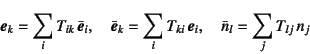
�Ƃ����W������̂ŁC��(3.19)��Cauchy�̒藝���
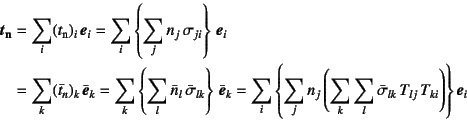
�Ƃ����W��B���ǂЂ��݂̍��W�ϊ����Ɠ�����
��B���邢�͍s��\������
�ƕ\���ł���B2�K�̃e���\�������͂��ׂē������W�ϊ����ɏ]���B
���̉��͂̍��W�ϊ����܂���ƁC��(3.32)��
�Ӗ��͂��������������Ղ��Ȃ�B���̎�(3.32)��
���E����C������x�N�g���łł������W�ϊ��s����悶���
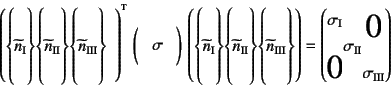
�Ƃ����\�����\�ɂȂ�B ���ӂ́C���̓e���\���̎���������x�N�g���Ƃ��� ���W�����ɁC���̉��̓e���\����ϊ��������̂ł���B �E�ӂ́C���̍��W�n�ł͒����͐������������Ă��Ȃ����Ƃ������Ă���B ���̎��̕����C�剞�͂̈Ӗ��𗝉����Ղ��l�͑�����������Ȃ��B
�Ђ��݃e���\�����̐ςЂ��ݐ����ƕ��Ђ��ݐ����i����f�Ђ��ݐ����j��
�����ł����悤�ɁC���̓e���\�����C
���ω��͂ƕ����͂�2�����ɕ����ł���B������`���Ă������B
�܂��C���ω���
��
�Œ�`����B������𐳂ɂ����Ð��� �ƍl���Ă����B �܂�C�����̂���[���ɂ����鉞�͏�Ԃ͎l���������� �������͂��Ă��āC�����Ð����Ə̂��Ă��邱�Ƃ���C���� ��`������B��(3.35)���C���ω��͂�3�{�͉��͂� ��1�s�ϗ� �ł�����B ���l�Ɏ�(3.14)�̑̐ςЂ��ݐ����� �Ђ��݂̑�1�s�ϗ� �ł���B
���̓e���\���������炱�̕��ω��͐�������菜�����������C
��(3.15)�Ɠ��l������
�e���\�������ƌĂ�
�Œ�`����B ���Ђ��݂Ɠ��l�C���̕����̓e���\�����������镨�̓_�� �������Ă����R�͂̂����̂���f���͐����ɑ�������B