 |
最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
前節の結論を踏まえ,任意の薄肉断面棒のねじりについて一般的な
定式化を試みる。ただ断面は閉断面
とする。閉断面は,あとで出てくる開断面
とは異なり,肉厚中心線が「端っこ」を持たずに
閉じた曲線になるような断面である。
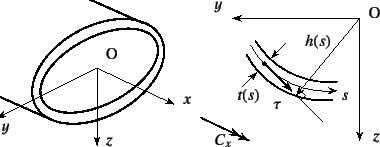
簡単のために,図-7.9のような![]() 軸回りのねじりを考え,
原点が断面のねじり中心であるとする。
軸回りのねじりを考え,
原点が断面のねじり中心であるとする。
薄肉円管の例からも明らかなように,せん断応力の肉厚方向の
分布は一様と近似していい。
したがってせん断応力![]() を直接扱うのでは
なく,図-7.9に示したように
その肉厚方向の代表値
を直接扱うのでは
なく,図-7.9に示したように
その肉厚方向の代表値![]() を定義し,
その
を定義し,
その![]() が肉厚中心線上に発生して抵抗しているものと
近似解釈する。
肉厚中心線に沿った新しい座標を
が肉厚中心線上に発生して抵抗しているものと
近似解釈する。
肉厚中心線に沿った新しい座標を![]() とし,肉厚中心線上の
任意点
とし,肉厚中心線上の
任意点![]() に発生しているせん断応力
に発生しているせん断応力![]() の作用線までの
原点からの距離を
の作用線までの
原点からの距離を![]() と
表す。肉厚は
と
表す。肉厚は![]() 方向に一様である必要は無く,
方向に一様である必要は無く,![]() と一般化しておく。
と一般化しておく。
このように考えて図-7.10の
ような
![]() の微分要素を取り出すと,
応力に
の微分要素を取り出すと,
応力に![]() を乗じた「一種の合応力」が図示したように
それぞれの面に発生していると考えていい。
この
を乗じた「一種の合応力」が図示したように
それぞれの面に発生していると考えていい。
この![]() 方向の力のつり合いは
方向の力のつり合いは
と7.1なる。これを![]() で積分すると
で積分すると
と表現できる。ここに![]() はある基準となる位置の
はある基準となる位置の![]() 座標値である。
棒をねじっているだけなので,円柱の場合と同様,
第1次近似としては軸方向の直応力は
発生せず,せん断応力だけで抵抗していると考えてもよさそうだ。
したがって上式右辺第2項の直応力に関する項は第1項に
比べて無視できる。これより
座標値である。
棒をねじっているだけなので,円柱の場合と同様,
第1次近似としては軸方向の直応力は
発生せず,せん断応力だけで抵抗していると考えてもよさそうだ。
したがって上式右辺第2項の直応力に関する項は第1項に
比べて無視できる。これより
という関係が成り立つ。あるいは新しく
とも書くことができる。つまり,薄肉断面を肉厚幅の水路とみなしたときに, そこを流れる水の流量がせん断流である。そして, 閉じた水路であるから当然総流量は一定で水路幅によらないから, せん断流もある断面内では一定になるのである。
このように,断面内の応力がせん断流で表現できるので,Saint-Venantの ねじりモーメントは
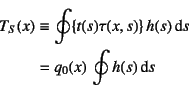
と定義していい。せん断流は断面内一定なので,最後の
式では![]() を積分の外に出すことができる。
ここで,図-7.11の
左図の網掛けが施された三角形の面積が
を積分の外に出すことができる。
ここで,図-7.11の
左図の網掛けが施された三角形の面積が
![]() で
あることを考えると,
上式の一周積分値は肉厚中心線で囲まれた部分の面積の2倍に
なっていることがわかる。つまり
で
あることを考えると,
上式の一周積分値は肉厚中心線で囲まれた部分の面積の2倍に
なっていることがわかる。つまり
である。ここに![]() は図-7.11の
細い曲線で描かれた肉厚中心線で囲まれた部分の面積である。
は図-7.11の
細い曲線で描かれた肉厚中心線で囲まれた部分の面積である。
したがって,せん断流がわかればSaint-Venantのねじりモーメントは
であり,この逆関係としてせん断応力は近似的に
と表現できることになる。![]() はあとで図-7.20にも
示すような,
はあとで図-7.20にも
示すような,![]() ,
, ![]() 軸に直交する座標である。
軸に直交する座標である。
一方図-7.11の右図に示したように,
断面肉厚中心線上の任意点![]() の
の![]() 方向の
変位成分を
方向の
変位成分を![]() とし,
とし,![]() 方向変位を
方向変位を![]() とすると,
直交曲線座標系でのこのせん断ひずみ成分は式(3.6)と同様
とすると,
直交曲線座標系でのこのせん断ひずみ成分は式(3.6)と同様
で定義できる。
円柱や円管の場合は![]() の
の![]() 方向の微係数を無視したが,
断面形が円形ではなくなったので,以下では考慮することにする。
原点がねじり回転角
方向の微係数を無視したが,
断面形が円形ではなくなったので,以下では考慮することにする。
原点がねじり回転角![]() の中心で,線形理論なので
回転角も小さく
の中心で,線形理論なので
回転角も小さく
![]() と
みなせるから,図からも明らかなように,近似的に
と
みなせるから,図からも明らかなように,近似的に
と考えていい。したがって上のひずみの定義に代入して
となる。一方Hookeの法則式(3.42)と
式(7.14) (7.15)から
と関係付けられる。
式(7.16)と式(7.17)から![]() を
消去して整理すると
を
消去して整理すると
がSaint-Venantのねじりモーメント![]() と
変位成分
と
変位成分![]() および
および![]() との関係になっている。
との関係になっている。
式(7.18)の両辺をある![]() から
から![]() 上で
閉断面内一周積分
上で
閉断面内一周積分
![]() から
から
![]() ,
,
![]() すると
すると
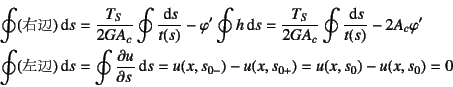
となる。左辺の演算で最後から二つ目の式は,断面内に
任意に選んだ積分始点![]() での
での![]() 方向変位
方向変位![]() の
食い違い量であり,閉断面である以上このような食い違いが
生じているはずはないから,それは零にならなければならず,
最終的に左辺の積分は零になる。
したがって,左辺右辺の積分演算結果を等値することにより
の
食い違い量であり,閉断面である以上このような食い違いが
生じているはずはないから,それは零にならなければならず,
最終的に左辺の積分は零になる。
したがって,左辺右辺の積分演算結果を等値することにより
という関係式を得,これからSaint-Venantのねじりモーメントは
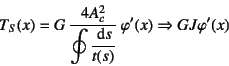
と表現できる。これより任意の閉断面のSaint-Venantのねじり定数
は
で定義すればいいことになる。
では前節の薄肉円管に対して,
上式の成否を確かめてみよう。この場合
なので,上の式(7.19)に代入することによって
となり,式(7.11)の値を得る。
箱形断面でできた橋梁部材や船体等では,断面の中がさらに仕切られて
多室になっていることがある。このような場合も同様の考え方で
ねじり剛性を算定できる。図-7.13のように,
左右外壁側の断面でのせん断流を
と置くと,点BおよびEでのせん断流の流れの連続性から,
中仕切り壁中のせん断流は
でなければならない。ねじり中心から
作用線までの距離を![]() で定義すると,2室
断面のSaint-Venantのねじりモーメントは,それぞれのせん断流を用いて
で定義すると,2室
断面のSaint-Venantのねじりモーメントは,それぞれのせん断流を用いて
で定義できる。ここでは![]() の向きを
の向きを![]() 座標と同じ向きに
定義してある。
座標と同じ向きに
定義してある。
![]() だから
だから
と表現できる。ここに![]() は
は![]() を
囲む閉曲線に沿った積分経路を示している。
を
囲む閉曲線に沿った積分経路を示している。
一方,式(7.17)はそれぞれの断面で
と書くことができるので,これと式(7.16)から
式(7.18)の代わりに
とも書くことができる。
これを例えば![]() に沿って周積分すると
に沿って周積分すると
つまり
という関係を得る。同様の演算を![]() に対しても行うと
に対しても行うと
となる。ここで左辺の![]() の各係数を
の各係数を
と定義しておいて,上2式を連立させて![]() について解くと
について解くと
となる。これを式(![]() )に代入すれば,
最終的にSaint-Venantのねじりモーメントを
)に代入すれば,
最終的にSaint-Venantのねじりモーメントを
![]() と
表現することができ,その関係式からねじり定数
が
と
表現することができ,その関係式からねじり定数
が
と求められる。
多室の一般論についても同様に算定できるが,
具体的な![]() の表現については参考文献等を参照のこと。
の表現については参考文献等を参照のこと。
任意の薄肉閉断面棒の
支配方程式は円柱・円管のそれと同じで,
つり合いは式(7.5)あるいは式(7.6)で,
境界条件も式(7.7)あるいは式(7.8)で
与えられる。
つまり任意の閉断面棒のねじり角![]() に関する
境界値問題の表現は,断面形状に依らずすべて同じになる。
断面形の違いは断面定数
に関する
境界値問題の表現は,断面形状に依らずすべて同じになる。
断面形の違いは断面定数![]() の違いとなってのみ現われ,初等梁理論等と
同じような棒理論が定式化された。
ただ厳密には,円柱や円管を除いた他の断面の場合には,
閉断面であっても一般には
次の節以降で議論するそりを考慮しなければならない
場合も多い。
これについては節-7.4で考慮する。
の違いとなってのみ現われ,初等梁理論等と
同じような棒理論が定式化された。
ただ厳密には,円柱や円管を除いた他の断面の場合には,
閉断面であっても一般には
次の節以降で議論するそりを考慮しなければならない
場合も多い。
これについては節-7.4で考慮する。