最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。

• 7.1.1 円柱のねじり
  • 7.1.1.1 薄肉断面部材の立体構造の力学
  • 7.1.1.2 ねじりによる変形
  • 7.1.1.3 合応力
  • 7.1.1.4 つり合い式と境界条件
    • 7.1.1.4.1 例題:
  
  
• 7.1.2 円管のねじり
  • 7.1.2.1 円管のねじり定数$J$
  • 7.1.2.2 薄肉円管のねじり定数$J$
    • 7.1.2.2.1 薄肉ということは:

7.1 円柱と円管のねじり

7.1.1 円柱のねじり

7.1.1.1 薄肉断面部材の立体構造の力学

前章までは，ある平面内のみで変形が生じる場合を扱ってきたが， 実際の構造物ではそういうことは稀であり， 立体的に挙動する構造系になっているのが普通である。 そういった構造系のある部材が棒でモデル化できる場合には， 前章までに扱ってきた軸方向の抵抗とそれに直交する二つの 軸回りの曲げ抵抗以外に，ねじり変形による抵抗が 発生することは容易に想像できる。 もちろんそれが設計を左右するようなレベルであるか否かは別問題だが， 例えば平面図がS字等に曲がった梁はもちろん，断面が2軸対称ではない1本の 直線梁の曲げにおいても，載荷位置によってはねじれが発生する。 ここでは主に鋼構造のモデルである薄肉うすにく断面棒部材 に焦点を絞り，ねじりの力学の基礎を概説する。 弾性論等の教科書等にあるねじり理論に， 断面が薄肉であることを利用した近似に基づく，構造力学と してのねじり理論の基礎である。

7.1.1.2 ねじりによる変形

図 7.1: 左端を固定された円柱のねじり
図 7.2: 円柱断面に生じる応力と回転変位

最も基本的な例として図-7.1にある円柱の ねじりを考えよう。 図中の2重矢印は，ねじり外力モーメント（ねじり外力）を， 普通の右ネジがその矢印方向に締まっていくような回転方向に 作用させることを意味する。章-4で 用いた曲げに対する基本的な仮定と同じように考えることにすると， この円柱をねじったときの変形の特徴は

• ねじられて回転したあとも，平面だった断面はほぼ平面のままであり，
• ねじられる中心の回りに断面は一様に回転する

と近似仮定できそうだ。この仮定を 図示したのが図-7.2の右図である。 原点回りに断面内の点$(r,\theta)$が$\varphi(x)$だけ 回転すると考えるのである。

図-7.2の右図を幾何学的に 考察すれば，点$(r,\theta)$の$x$, $y$, $z$方向の各変位成分は

$$\begin{array}{l} u_x(x,y,z)\equiv 0, \quad \left[\mbox{最低... ... \simeq r\varphi\cos\theta=y \varphi(x) \end{array}\eqno{(a)}$$

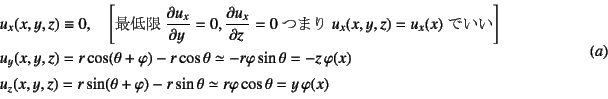
となる。ただし，それぞれの式の 第2式から第3式への近似では，ねじりに よる回転角が微小である条件，つまり $\left\vert\varphi(x)\right\vert\ll 1$を 用いている。 この式($a$)をひずみの定義式(3.6)に 代入すると，零でない成分は

$$\epsilon_{xy}=-\dfrac12 z \D*{\varphi(x)}{x}, \quad \epsilon_{zx}=\dfrac12 y \D*{\varphi(x)}{x} \eqno{(b)}$$

の二つだけであることがわかる。

7.1.1.3 合応力

式($b$)をHookeの法則式(3.42)に 代入すれば，応力は

$$\sigma_{xy}=-G z \varphi'(x)=-Gr\sin\theta\varphi'(x), \quad \sigma_{zx}= G y \varphi'(x)=Gr\cos\theta\varphi'(x)$$ (7.1)

の2成分だけが非零である。$(\mbox{ })'$は$x$に関する 微係数を表し，以下でも用いる。また$G$はせん断弾性係数である。 合応力の1成分としての$y$方向のせん断力を， 最初の応力成分を用いて算定してみると

$$V_y=\int_A \sigma_{xy}\dint A= \int_0^{r_o}\!\!\!\dint r \i... ...{r_o} r^2\dint r \int_0^{2\pi}\!\!\! \sin\theta \dint\theta=0$$

のように 零になる。同様に$z$方向のせん断力も零である。 次に， 式(4.11)の曲げモーメントを念頭に置いて，この 断面内のせん断応力で定義できる合応力を想定すると， もう一つの断面力である$x$軸回りのSaint-Venantのねじりモーメント が

$$T_S(x)\equiv \int_A \left(-z \sigma_{xy}+y \sigma_{zx}\right)\dint A \index{=ts@$T_S$}%$$ (7.2)

と定義できそうだ。符号は，正の断面での正のモーメントの向きを2重矢印で 示したときに，それが$x$の正方向を向くように定義してある。 式(7.1)を式(7.2)に代入して整理すると

$$T_S(x)=G\left\{\int_A (y^2+z^2)\dint A\right\}\varphi'(x) \Rightarrow GJ \varphi'(x)$$ (7.3)

となる。ここに$J$は，次式で 定義されるSaint-Venantのねじり定数 で

$$J\equiv\int_A (y^2+z^2)\dint A = \int_0^{r_o}\!\!\!\dint r\... ...} r\dint\theta r^2 = \dfrac{\pi}{2} r_o^4 \index{=j@$J$}%$$ (7.4)

という値を持ち，円柱の場合には断面の極2次モーメント に一致している。その次元は断面2次モーメントと 同じく $[\mbox{長さ}]^4$である。$\varphi'$はねじり率 と呼ばれる。Saint-Venantのねじりモーメントはねじり率 に比例し，その比例抵抗係数$GJ$はSaint-Venantのねじり剛性 と呼ばれる。

7.1.1.4 つり合い式と境界条件

図 7.3: Saint-Venantのねじり力に関するつり合い

結局，断面に発生した抵抗力はこのSaint-Venantのねじりモーメントだけ なので，図-7.3のような 微分要素におけるモーメントのつり合いから

$$\left(T_S+\D*{T_S}{x}\dint x\right)-T_S=0$$

がつり合い式であることは明らかである。 よって長さ$\ell$の棒のねじりのつり合い式は

$$T_S'(x)=0, \qquad 0<x<\ell$$ (7.5)

と表される。一様断面の場合のつり合い式を ねじり回転角$\varphi(x)$で表すと， 式(7.3)を上式に代入して

$$GJ \varphi''(x)=0 \index{つりあいしき@つり合い式 (equili... ...torsion (サン\protect\mbox{}-\protect\mbox{}ブナンのねじりの)}$$ (7.6)

となる。 なお，ここでは分布外力トルクのようなものを無視している。

境界条件の代表的なものは図-7.1の両端の条件で あろう。つまり，左端のような回転固定の条件と，右端のような ねじり外力を与える条件との二つである。図-7.1に 定義したねじり外力の$C_x$の方向を正と すると，一般的な境界条件 は

$$\varphi=\mbox{与えられる}\quad\mbox{あるいは}\quad n_i T_S=(C_x)_i \quad (i=1,2)$$ (7.7)

と書くことができる。ただし簡単のために式(4.24)の 記号$n_i$を用い，左端$x=0$での条件は$i=1$の場合，右端$x=\ell$での 条件は$i=2$の場合とした。 もちろん力の境界条件もねじり回転角$\varphi$で表すと

$$\varphi=\mbox{与えられる}\quad\mbox{あるいは}\quad n_i \left(GJ \varphi'\right)=(C_x)_i \quad (i=1,2)$$ (7.8)

となる。

図 7.4: 円柱断面に生じるせん断応力分布と変形

7.1.1.4.1 例題:

まず，図-7.1の問題を解いておこう。 右端で与えるねじり外力$C_x$を$T_0$と記すことにすれば境界条件は

$$\varphi(0)=0, \quad T_S(\ell)=GJ\varphi'(\ell)=T_0$$

である。つり合い式(7.6)の一般解は

$$\varphi(x)=a x+b$$

となるから，上の境界条件にこれを代入して積分定数$a$, $b$を決定すると， 結局

$$a=\dfrac{T_0}{GJ}, \quad b=0$$

を得る。したがって，解は

(7.9)

となる。図-7.4の右側に， ねじりによる円柱母線の変形を模式的に示した。 特に$y$, $z$軸上の応力分布も式(7.1)に 式(7.9a)を 代入すると求めることができ，図-7.4の左側に 示したようになる。 原点回りのねじり抵抗が発生しているのがわかる。

7.1.2 円管のねじり

7.1.2.1 円管のねじり定数$J$

さて次に円管をねじってみよう。円管のねじり変形の特徴も， 円柱のそれと同じだろうと推測できることから， 前節の式(7.1)の応力分布までは同じ結論になると考えていいだろう。 これをSaint-Venantのねじりモーメントの定義式(7.2)に 代入すると，$r_i$が内半径で外半径が$r_o$の円管の場合には

$$T_S(x)\equiv \int_A \left(-z \sigma_{xy}+y \sigma_{zx}\ri... ..._o}\!\!\!\dint r\int_0^{2\pi} r\dint\theta r^2 G \varphi'$$

のように積分範囲が円柱の場合と異なるだけである。 結局Saint-Venantのねじり定数 が

$$J=\int_{r_i}^{r_o}\!\!\!\int_0^{2\pi} r^3\dint r\dint\theta= \dfrac{\pi}{2}\left( r_o^4 -r_i^4 \right) \eqno{(*)} y$$

という値を持つことになる。$J$の定義そのものは円柱のときと同じで， 前節の境界値問題の基礎式も円柱のそれと同じである。 せん断応力分布を図-7.5に示した。

7.1.2.2 薄肉円管のねじり定数$J$

図 7.5: 円管のせん断応力分布
図 7.6: 薄肉円管の断面諸量

もし円管の肉厚が非常に薄い場合には，この断面定数$J$の 算定でさらに合理的な近似ができそうだ。 例えば図-7.6のように 肉厚中心線の半径を$r_c$として肉厚を$t$としたとき

$$r_c\gg t \quad\mbox{あるいは}\quad \left(\mbox{径厚比}\right)\equiv\dfrac{D}{t}\gg 1, \quad D\equiv 2r_c$$

で あるような管は，鋼構造ではよく用いられる薄肉円管である。 この半径$r_c$と肉厚$t$を用いて式($*$)を表現し直すと

$$J=\dfrac{\pi}{2}\left\{\left(r_c+\dfrac{t}{2}\right)^4- \le... ...2\pi r_c^3 t \left\{1+\left(\dfrac{t}{D}\right)^2\right\}$$

となる。したがって上述のように，断面内の二つの 寸法同士の大小関係が著しい場合には， 最後の表現の括弧内の第2項は第1項に 比べて無視できるくらい小さいと考えていい。 したがって，薄肉円管のSaint-Venantのねじり定数 は

$$J\simeq 2\pi r_c^3 t$$ (7.10)

と近似できる。

図 7.7: 薄肉円管断面に発生するせん断応力分布の近似

7.1.2.2.1 薄肉ということは:

この結論は，実は薄肉断面部材 であることを別の角度から近似解釈しても得ることができる。 つまり，実際には図-7.7の左図に示したように 分布するはずの応力を，肉厚が非常に薄いために，その 厚さ方向への分布を近似し，同図の右図のように 肉厚方向には一様なせん断応力が生じているものと近似してみるのである。 肉厚が非常に薄いため，本当は線形分布する応力の外径側と 内径側での応力差はとても小さくなる。 したがって，その平均値でもある肉厚中心線上での応力を， その場所の応力の代表値と解釈して

$$\tau\equiv G \varphi'(x) r_c$$

の値のせん断応力が，肉厚方向には一様に分布していると近似するのである。 こうすることによってSaint-Venantのねじりモーメントは， 微分面積を $\dint A=t r_c\dint\theta$と近似していいから

$$T_S(x)=\int_A \tau r_c \dint A= G \varphi'(x)\int_0^{2\pi} t r_c^3\dint\theta$$

と算定できる。この式と式(7.3)の表現を 比較すると，$J$は右辺の積分項で

$$J= \int_0^{2\pi} t r_c^3 \dint\theta = 2\pi r_c^3 t$$ (7.11)

となり，式(7.10)と一致する。

すなわち肉厚が非常に薄い場合には， その薄い肉厚方向への力学的挙動をある程度簡略化しても， 工学的には十分な精度を持つ理論を 定式化できることがわかる。章-4の梁理論の場合も， 長さ方向に比べてその寸法が比較的小さい断面方向の応力分布を 簡略化することにより，扱い易く精度も失われない 初等梁理論を定式化できた。ここでも上の近似のように， 断面を構成する二つの寸法の間に「薄肉」という極端な大小関係が ある場合には，比較的小さい寸法である肉厚方向への応力分布等を 簡略化しても，精度が失われないことが明らかになった。 次の節では，このような考えに基づき，任意の薄肉閉断面棒部材の ねじり理論を定式化してみよう。

図 7.8: 両端固定丸棒のねじり

1. 図-7.8の 両端が固定された丸棒の中央にねじり外力$T_0$を作用させた ときの，任意断面のねじり角を求めよ。 載荷点での不連続の条件については，曲げ問題での条件 式(4.44) (4.45)を参考にして 式(7.7)の境界条件から求めよ。

最新版を正確に読むためには pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。