 |
最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
ここでは,最も基礎的な構造部材である柱の分岐座屈についての 定式化をし,いくつかの例題を解く。 柱の分岐座屈を解析するための理論は,軸力の作用下で曲がる 部材,つまり「柱」に作用する外力に対して曲げ変形で抵抗する「梁」として 挙動する部材の力学理論になるので,よく梁-柱理論 と呼ばれる。 ただ座屈後の柱の抵抗は平板等に比べると比較的小さいため,座屈荷重レベル 付近での挙動を把握すれば工学的には十分なことが多い。 したがってここでは,厳密な 有限変位理論としてではなく,節-6.2.4でも 定式化した比較的変位の小さい範囲の理論としての梁-柱の 基本的な境界値問題を中心にして定式化する。
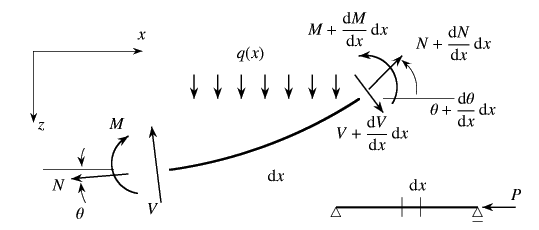
1本のまっすぐな等断面・均質材料の棒に軸力![]() が作用し,
曲がってつり合っている状態を考え,図-6.17の
ように分布外力も曲げに関するものだけが作用しているものとする。
まず
が作用し,
曲がってつり合っている状態を考え,図-6.17の
ように分布外力も曲げに関するものだけが作用しているものとする。
まず![]() 方向の力のつり合いより
方向の力のつり合いより
となる。ここで
![]() の近似を行い
の近似を行い
と置くと,最終的に上式は
となる。
同様に![]() 方向の力のつり合いより
方向の力のつり合いより
となり,また左端回りのモーメントのつり合いから
を得る。 最後のモーメントのつり合いのみ章-4の 微小変位理論の式(4.18)と一致する。
さて
ここで対象としているのは,前節同様,大きな軸力の影響で
曲がる部材の挙動なので,
座屈点のごく近傍では軸力がその他の断面力よりも比較的
大きいと考えていい。すなわち,大まかなオーダー比較として
程度にあるものと近似していいことにする。
すると,上で得たつり合い式のうち
式(6.21)の第2項は第1項に比べて非常に小さいが,
式(6.22)の第2項は第1項とほぼ同じオーダーになると
考えていい。
したがって,式(6.23)を式(6.22)に
代入して![]() を消去した上で,
この近似によって修正した式(6.21)も列挙すると
を消去した上で,
この近似によって修正した式(6.21)も列挙すると
となる。軸力のつり合い式(6.24a)は 微小変位理論のそれと同じになる。 そして,曲げのつり合い式(6.24b)の第2項が 線形の初等梁理論には無い非線形付加項で,座屈解析に最も重要な項である。
境界条件も同様の演算を行えば,章-4の
式(4.24)で定義した記号![]() を用いて
を用いて
となる。せん断力に関する条件の内力第2項が初等梁理論と異なり, 重要な項である。
ここで基本的に解きたい対象は,図-6.1のように
端部に軸力![]() が作用した系なので,式(6.25a)に
この境界条件を代入して式(6.24a)を解くと
が作用した系なので,式(6.25a)に
この境界条件を代入して式(6.24a)を解くと
が軸力に関する解となる。したがって,この結果を上のつり合い式と
境界条件式に代入して整理すると,最終的に梁-柱理論の
曲げに関するつり合い式
が
となる。 元々は非線形の支配方程式であったが,オーダー比較で近似をした結果 軸力が一定になるので,ここまでの表現では見かけ上は 定数係数の線形理論になっているのは興味深い。
あとは構成方程式が必要となるが,これは 初等梁理論と同じ式(4.13b)で与えられると考えていい。 厳密なアプローチに ついては節-6.6および節-E.4にその概要を 示してあるが,梁-柱理論として整合する 構成方程式は,軸力と軸ひずみに関する方を
(6.29)
と近似して捉えるべきであることがわかっている。
伸びひずみの第2項が,たわむことによる非線形的な成分である。
線形の伸び![]() はたわみ角
はたわみ角![]() よりもさらに一つ
オーダーの小さい量なので,この非線形項が無視できなくなっている。
しかし通常,梁-柱理論の枠の中でこの軸力の
構成方程式が必要になることは稀なので,ここでは考えないことにする。
実際ある程度細長い棒の場合で,比較的小さい変位の範囲内では,
軸の伸びひずみの影響は
曲げによるひずみに比べて無視できるくらい小さいのも事実である。
よりもさらに一つ
オーダーの小さい量なので,この非線形項が無視できなくなっている。
しかし通常,梁-柱理論の枠の中でこの軸力の
構成方程式が必要になることは稀なので,ここでは考えないことにする。
実際ある程度細長い棒の場合で,比較的小さい変位の範囲内では,
軸の伸びひずみの影響は
曲げによるひずみに比べて無視できるくらい小さいのも事実である。
したがって,式(4.13b)の曲げモーメントと
曲率の関係を上の式に代入すると,最終的にたわみ![]() で
表した梁-柱理論のつり合い式(6.27)は
で
表した梁-柱理論のつり合い式(6.27)は
となり,式(6.28)の境界条件は
で表される。
式(6.26)のように軸力を一定とすることが
できたため,変位した状態でつり合いを考えたにもかかわらず,
式(6.29)の軸力の構成則以外は,誘導された
梁-柱理論が定数係数の線形理論になっているのは
上述の通りである。
式(6.31a)のせん断力の境界条件に軸力![]() の
成分が含まれているのは,変形後の軸方向が元の
の
成分が含まれているのは,変形後の軸方向が元の![]() 方向と
たわみ角の分だけ傾いているからである。
その右端での様子を図-6.18に例示した。
方向と
たわみ角の分だけ傾いているからである。
その右端での様子を図-6.18に例示した。
もちろん,軸方向の分布外力が存在する場合には
式(6.26)のような一定軸力にはならない。
しかしその場合でも,軸方向の境界値問題が曲げと独立して
いるために,軸方向の力のつり合い式(6.24a)に
分布外力を含め,
適切な境界条件から![]() をまず算定しておけば,同じように解ける。
例えば図-6.19に示したように柱の自重に
相当する等分布外力が作用している柱の場合には,軸力が
をまず算定しておけば,同じように解ける。
例えば図-6.19に示したように柱の自重に
相当する等分布外力が作用している柱の場合には,軸力が
と求められる。したがって,
この式を式(6.24b)に代入して,
軸方向の等分布外力がある場合の梁-柱のつり合い式は
のような変数係数の微分方程式6.4になる。![]() の
ときのこの式は,ある変数変換をすると
の
ときのこの式は,ある変数変換をすると![]() 次のBessel方程式になるので,
その解は
次のBessel方程式になるので,
その解は![]() 次のBessel関数
次のBessel関数
![]() になる。
詳細については文献[73]等を参照のこと。
になる。
詳細については文献[73]等を参照のこと。
誘導された理論で最も基本的な系,つまり図-6.20に示した
両端単純支持された棒の問題を解いておこう。この場合は分布外力が
存在しないので,つり合い式は式(6.30)より
であり,境界条件は両端共に式(6.31)より
で与えられる。ここに![]() は
は![]() に関する微係数であり,以下用いる。
ただしこの節に限っては,少し物理的な理解を深めるために,
標準的な微分方程式の解法を用いていないことに注意して欲しい。
その標準的な解法は次の節で示す。
さて図より明らかなように左右対称の系なので,両端のせん断反力も
零であることが容易に予想される(としては本当はいけないよ)。
したがって,上式のつり合い式を1回積分しても,
せん断力の境界条件と対称条件を考慮すると
に関する微係数であり,以下用いる。
ただしこの節に限っては,少し物理的な理解を深めるために,
標準的な微分方程式の解法を用いていないことに注意して欲しい。
その標準的な解法は次の節で示す。
さて図より明らかなように左右対称の系なので,両端のせん断反力も
零であることが容易に予想される(としては本当はいけないよ)。
したがって,上式のつり合い式を1回積分しても,
せん断力の境界条件と対称条件を考慮すると
となる。さらにもう1回積分しても,上式の単純支持の境界条件を考慮すると
を得る。そこで,曲げモーメントの構成則を用いると第1項は曲げ
モーメントそのものであり,第2項を右辺に移項すると,この式は
という表現とみなすことができる。
この式の物理的な意味を理解するために,図-6.21のように
たわんだ状態を考えてみる。すると,
式(6.32)の右辺
![]() は,
ある着目した断面から眺めたときに,
端部の軸力
は,
ある着目した断面から眺めたときに,
端部の軸力![]() がたわみ
がたわみ![]() と作るモーメントになっていることは明らかだろう。
そしてその着目した断面には図のような内力曲げモーメント
と作るモーメントになっていることは明らかだろう。
そしてその着目した断面には図のような内力曲げモーメント![]() が生じて
つり合っている。つまり,式(6.32)は,
たわんだ状態における内力曲げモーメント
が生じて
つり合っている。つまり,式(6.32)は,
たわんだ状態における内力曲げモーメント![]() と端部の
軸力
と端部の
軸力![]() が作る付加モーメント
が作る付加モーメント
![]() との,
モーメントのつり合いそのものであることがわかる。
すなわちつり合い式(6.30)の第2項は,
たわんだ状態の断面で考慮すべき,端圧縮外力が
作る付加的な曲げモーメント成分であることがわかる。
この式を見れば,変形した状態でつり合いを考えようとする幾何学的非線形問題の
一端が理解できると思う。
との,
モーメントのつり合いそのものであることがわかる。
すなわちつり合い式(6.30)の第2項は,
たわんだ状態の断面で考慮すべき,端圧縮外力が
作る付加的な曲げモーメント成分であることがわかる。
この式を見れば,変形した状態でつり合いを考えようとする幾何学的非線形問題の
一端が理解できると思う。
さて本題に戻って解析を続けよう。2回積分して得た上式(![]() )は2階の
常微分方程式であり,通常の手段を用いれば
)は2階の
常微分方程式であり,通常の手段を用いれば
が一般解である。ただし軸力![]() は圧縮で正としているので
は圧縮で正としているので
と定義した。式(![]() )を両端のたわみが零になる
境界条件に代入すると,結局
)を両端のたわみが零になる
境界条件に代入すると,結局
であればいい。したがって![]() であると同時に
であると同時に
が成立していなければならない。
この式(![]() )は二つの可能性を提供して
いる。一つは
)は二つの可能性を提供して
いる。一つは![]() であるが,これだと結局
であるが,これだと結局![]() が
恒等的に零ということになり,曲げ変形は発生しないことになる。
もちろんこれは座屈前の解であり,正解ではあるが欲しい答ではない。
今ここで問題にしているのは
「軸力のみの作用で曲がる解が存在するか否か」である。
したがって
が
恒等的に零ということになり,曲げ変形は発生しないことになる。
もちろんこれは座屈前の解であり,正解ではあるが欲しい答ではない。
今ここで問題にしているのは
「軸力のみの作用で曲がる解が存在するか否か」である。
したがって![]() となる解の存在を捜す必要がある。
それには式(
となる解の存在を捜す必要がある。
それには式(![]() )の二つ目の可能性,つまり
)の二つ目の可能性,つまり
であればいいことがわかる。したがって,もし
になるような![]() が存在した場合には,
が存在した場合には,![]() の解を
持つことができる。
式(6.33)の定義を上式(
の解を
持つことができる。
式(6.33)の定義を上式(![]() )に代入すると
)に代入すると
で定義される限界荷重
![]() に
外力が達したときに
に
外力が達したときに![]() でも
よくなり,座屈が発生する可能性があるということになる。
通常は零から荷重
でも
よくなり,座屈が発生する可能性があるということになる。
通常は零から荷重![]() を増加させていくので,
最初の分岐座屈点は
を増加させていくので,
最初の分岐座屈点は
![]() の最小値,つまり
の最小値,つまり![]() のときの
のときの
が最小の座屈荷重となる。これが基本的なEuler座屈
であり,この![]() が最も基本的な柱の
座屈荷重で,Euler荷重
と呼ばれている。
結局,積分定数
が最も基本的な柱の
座屈荷重で,Euler荷重
と呼ばれている。
結局,積分定数![]() は不定のままだから,求められたたわみ形状は
は不定のままだから,求められたたわみ形状は
となり,大きさは不定だがsine曲線の半波長の形状で
座屈しようとすることがわかる。
このような座屈形状を座屈モード
と呼んでいる。
梁-柱理論が比較的変位の小さい近似理論として
定式化されていることを考えれば,座屈後にどうなるかという
情報,つまり![]() を決定する情報を与えてくれないのは仕方がない。
ちょうど図-6.7で実線が
を決定する情報を与えてくれないのは仕方がない。
ちょうど図-6.7で実線が
![]() には
至らなかったのと同じ理由だ。
座屈後の挙動を知る必要がある(図-6.7の破線を
描きたい)場合には,近似の無い有限変位理論を用いる必要がある。
には
至らなかったのと同じ理由だ。
座屈後の挙動を知る必要がある(図-6.7の破線を
描きたい)場合には,近似の無い有限変位理論を用いる必要がある。
通常の設計では,設計断面の応力を算定し,
それを基準値(強度)と比較して安全性を確認する。
この座屈荷重に対応する軸応力を計算すると
となる。ここに![]() は棒の断面積であり
は棒の断面積であり
(6.37)
と定義した。![]() は
断面の回転半径
と呼ばれ,断面定数だけで計算できる長さの次元を持ったパラメータで,
断面寸法を代表する長さと考えれば
いい。
は
断面の回転半径
と呼ばれ,断面定数だけで計算できる長さの次元を持ったパラメータで,
断面寸法を代表する長さと考えれば
いい。![]() は細長比ほそながひ
と呼ばれ,断面寸法と比較したときの棒の細長さの程度を表すパラメータである。
式(6.36)から明らかなように,
座屈応力は細長比の2乗に反比例している。
したがって,柱が細長くなればなるほど急激に座屈強度は低くなる。
結果を図-6.22に示した。
もちろん,材料の降伏応力
を
は細長比ほそながひ
と呼ばれ,断面寸法と比較したときの棒の細長さの程度を表すパラメータである。
式(6.36)から明らかなように,
座屈応力は細長比の2乗に反比例している。
したがって,柱が細長くなればなるほど急激に座屈強度は低くなる。
結果を図-6.22に示した。
もちろん,材料の降伏応力
を
![]() としたとき,縦軸が
としたとき,縦軸が
![]() を
越える部分はあまり意味が
無いが,それについては別の節で概説する。
この曲線をEuler曲線
と呼ぶ。
を
越える部分はあまり意味が
無いが,それについては別の節で概説する。
この曲線をEuler曲線
と呼ぶ。
ところで,式(6.34)の![]() の場合の値は何だろう。
例えば
の場合の値は何だろう。
例えば![]() の値は式(6.35)のEuler荷重の4倍になる。
もし,この単純梁を注意深く圧縮していき,例えば
棒の中央をちょっとだけ手で支えておくことによってEuler荷重後もまっすぐな
ままで維持できたとすると,その4倍の外力に達したときに
もう一つの分岐点が存在することになる。そして,そのときの
たわみの解は式(
の値は式(6.35)のEuler荷重の4倍になる。
もし,この単純梁を注意深く圧縮していき,例えば
棒の中央をちょっとだけ手で支えておくことによってEuler荷重後もまっすぐな
ままで維持できたとすると,その4倍の外力に達したときに
もう一つの分岐点が存在することになる。そして,そのときの
たわみの解は式(![]() )とは異なり
)とは異なり
となるので,座屈した瞬間の形状はsine曲線の一周期分に 相当する。3次モードまでを図-6.23に示した。 このような高次の座屈は通常は発生しないが,例えば後述のように, 柱の中間にバネ支持等を設けることによってちょっとでも拘束すると, この高次モードに対応する座屈荷重レベルまで強くできることも意味する。 そういう意味からは,高次のものも含め座屈モードは設計上も非常に 重要な概念である。
ここでは固有値問題の標準的な解法を用いて,柱の座屈荷重を
求めよう。図-6.24に示した棒を柱と呼ぶことにするが,
つり合い式は式(6.33)の![]() を用いると
を用いると
と書くことができる。
境界条件は![]() で
で![]() ,
, ![]() 。
右端の
。
右端の![]() では,ここも
では,ここも![]() を用いて
を用いて
となっている。
常微分方程式を解析する常套手段として
![]() を
上のつり合い式の
を
上のつり合い式の![]() に代入すると,
その
に代入すると,
その![]() についての特性方程式が
についての特性方程式が
となる。![]() が2重根で
が2重根で
![]() が他の2解だから,
一般解は
が他の2解だから,
一般解は
![]() と
と
![]() で
で
となる。これを境界条件に代入すると順に
となるので,行列表示をすると
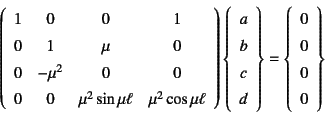
となる。右辺は零であるから,もし左辺の係数行列が正則で逆行列が 存在するなら,すべての積分定数は零になる。それは 座屈前の曲がらない解であり,よく無意味な解 と呼ばれる。
ここでは座屈する可能性を検討しているので,
積分定数のいくつかが非零である可能性,つまり上式が無意味な解を
持たない可能性を探る必要があり,
それはこの係数行列が正則でなくなる可能性を探ることに等しい。
正則でない条件は,この係数行列の行列式が零になることである。
第1列の1行目以外がすべて零なので,行列式は右下の![]() の
部分行列を用いて簡単に計算でき
の
部分行列を用いて簡単に計算でき
という条件を得る。
したがって,最小の座屈荷重が
と求められる。つまり式(6.35)で定義したEuler荷重
の![]() の軸力で座屈する。求められた結果を上の連立方程式に
再度代入して積分定数を計算すると,結局
の軸力で座屈する。求められた結果を上の連立方程式に
再度代入して積分定数を計算すると,結局![]() 以外は零になり,座屈モードは
以外は零になり,座屈モードは
と計算できる。![]() は不定であるが,
座屈モードはsine曲線の
は不定であるが,
座屈モードはsine曲線の![]() 波長分に相当する。こういった問題を
微分方程式の固有値問題
と呼び,
波長分に相当する。こういった問題を
微分方程式の固有値問題
と呼び,![]() が固有値に,座屈モードが固有関数に相当している。
座屈荷重はこのように境界条件に強く支配され,値が大きく異なる。
その違いを明確化するために
が固有値に,座屈モードが固有関数に相当している。
座屈荷重はこのように境界条件に強く支配され,値が大きく異なる。
その違いを明確化するために
と6.5置き,座屈係数![]() で
境界条件の影響を表現することがある。
代表的な境界条件の場合の座屈係数を図-6.25に
示しておいた。
で
境界条件の影響を表現することがある。
代表的な境界条件の場合の座屈係数を図-6.25に
示しておいた。
さて,Euler荷重で座屈する単純梁の座屈モードはsine曲線の半波長分で
あったのに対し,柱のモードは![]() 波長分になっている。
つまり図-6.26に示した座屈形状を見て比較すると
明らかなように,
「長さ
波長分になっている。
つまり図-6.26に示した座屈形状を見て比較すると
明らかなように,
「長さ![]() の柱」が座屈するときの状況は,「長さ
の柱」が座屈するときの状況は,「長さ![]() の
単純支持された棒」が座屈するときの状況と一致していることがわかる。
したがって,Euler荷重公式の
の
単純支持された棒」が座屈するときの状況と一致していることがわかる。
したがって,Euler荷重公式の![]() を
を![]() にした外力が
柱の座屈荷重になっており,それはEuler荷重の
にした外力が
柱の座屈荷重になっており,それはEuler荷重の![]() になる。
このことから,上の
になる。
このことから,上の![]() の見方を変えて式(6.41)を
の見方を変えて式(6.41)を
と読み替えることもできることがわかる。
この![]() は有効座屈長
と呼ばれ,座屈モードのsine半波分の長さに相当する。
は有効座屈長
と呼ばれ,座屈モードのsine半波分の長さに相当する。![]() は有効座屈長係数
と呼ばれる。
この
は有効座屈長係数
と呼ばれる。
この![]() の長さは,上の例で述べたように境界条件を考慮してどのような
座屈モード
で座屈するのか想像すれば,おおよその値を推定できる。
実際の骨組の一部材の座屈を考える場合には,部材毎の境界条件が,
ここで示したような理想的なものではなく,接合された相隣接する
部材同士がお互いにお互いを弾性支持している
状態になっていることに注意する必要がある。
その場合も有効座屈長の考え方でおおよその座屈荷重を見積もることもできそうだ。
個々の詳細な結果や例については参考文献[73]等を
参照のこと。
の長さは,上の例で述べたように境界条件を考慮してどのような
座屈モード
で座屈するのか想像すれば,おおよその値を推定できる。
実際の骨組の一部材の座屈を考える場合には,部材毎の境界条件が,
ここで示したような理想的なものではなく,接合された相隣接する
部材同士がお互いにお互いを弾性支持している
状態になっていることに注意する必要がある。
その場合も有効座屈長の考え方でおおよその座屈荷重を見積もることもできそうだ。
個々の詳細な結果や例については参考文献[73]等を
参照のこと。
という固有方程式の解であることを示し,その結果, 座屈係数が図-6.25に示された値になることを 数値的に確認せよ。
骨組中の1部材のモデルとしては不十分だが,一つの簡単な
例として図-6.28のように柱の先端が線形バネで
支持されている場合の曲げ座屈を解いておこう。
これは,ちょっとした支持が座屈強度を大きく変化させる一例と考えて欲しい。
境界条件は普通の柱の場合とほとんど同じだが,右端のせん断力の
境界条件において式(4.29)の左辺第2項のような
バネによる付加項を考慮する必要がある。
つまり,この梁-柱の場合の右端のせん断力の
境界条件は式(6.31a)で
![]() とでも
考えればいいから,
とでも
考えればいいから,![]() なので
なので
と改訂すればいい。したがって,他の条件も含めた境界条件は
となる。したがって,一般解の式(6.38)を
代入して整理すると順に
と表される。これを行列表示して,係数行列の行列式が零になる条件から 座屈荷重を求めればいい。この係数行列も比較的簡単な形になっている ので,容易に
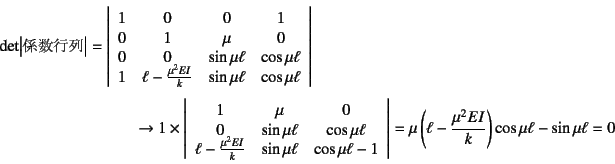
となることがわかる。したがって,式(4.41)で
定義したバネに関するパラメータ![]() を用いて書き直すと
を用いて書き直すと
が座屈荷重を求めるための特性方程式になる。![]() に関して
陽な表現になっておらず,
座屈荷重は数値的にしか計算できないが,
まずは二つの特別な場合6.6を考えておこう。
に関して
陽な表現になっておらず,
座屈荷重は数値的にしか計算できないが,
まずは二つの特別な場合6.6を考えておこう。
一つの特殊な状態はバネが存在しない場合で,![]() とすれば
いいから特性方程式(6.44)は
とすれば
いいから特性方程式(6.44)は
となる。これはまさに式(6.39)で得た
普通の柱の座屈に関する特性方程式であり,
座屈荷重はEuler荷重の![]() , (
, (![]() )になる。
もう一つの特別な場合はバネが剛になった場合である。
この場合には,式(6.44)で
)になる。
もう一つの特別な場合はバネが剛になった場合である。
この場合には,式(6.44)で
![]() という
極限を考えればよく,結局
という
極限を考えればよく,結局
| (6.45) |
が特性方程式になる。
これは上の演習
問題6-2の3番に
出した片端固定・片端単純支持梁の座屈の特性方程式に一致し,
座屈係数は
![]() である。したがって,剛ではない
一般的なバネ定数の場合の座屈係数は,そのバネの剛性を代表する
パラメータ
である。したがって,剛ではない
一般的なバネ定数の場合の座屈係数は,そのバネの剛性を代表する
パラメータ![]() の
大きさに依存して,この2者の座屈係数の中間の値をとることになる。
類似の問題を節-6.5.1でも再度解析するが,
式(6.44)の結果を図-6.29に示しておいた。
バネ定数の増加に対する座屈係数の増加の速さが比較的大きいことがわかり,
ちょっとした拘束や支持等の補強によって座屈強度を上げることが
期待できることを示している。
の
大きさに依存して,この2者の座屈係数の中間の値をとることになる。
類似の問題を節-6.5.1でも再度解析するが,
式(6.44)の結果を図-6.29に示しておいた。
バネ定数の増加に対する座屈係数の増加の速さが比較的大きいことがわかり,
ちょっとした拘束や支持等の補強によって座屈強度を上げることが
期待できることを示している。
境界条件をより良く理解するために,もう一つだけ面白い問題を 解いておこう。それは図-6.30に示したように, 柱の先端に作用している軸圧縮力の向きが常に柱の 軸線に沿った方向になるように保たれている場合である。 このような力を追随力 とか,一般的には非保存 力6.7と呼ぶ。具体的にはロケットの推力や庭の水撒きに使う ホース先端部分を思い浮かべて欲しい。つまり, ホースを地面に置いたまま水量を増していくと, ある水量以上になるとホースが その向きをいろんな方向に変えながらのた打ち回るのが観察される。 これも一種の不安定現象であろうから, 梁-柱理論で解けないだろうか。
図のように変形した状態のつり合いを考えた場合にも,軸力に
関する右端の境界条件は近似的には前の例と同じと考えてよく,
軸力は
![]() と考えていいはずだ。
したがって通常の梁-柱の基礎方程式を用いていい。
前節の柱の場合と異なる境界条件は,右端のせん断力に関するものだけで
と考えていいはずだ。
したがって通常の梁-柱の基礎方程式を用いていい。
前節の柱の場合と異なる境界条件は,右端のせん断力に関するものだけで
となる。見かけ上,初等梁理論のせん断力の境界条件に一致することに
注意して欲しい。
したがって式(6.38)の一般解をすべての
境界条件に代入すると
となるので,行列表示すると
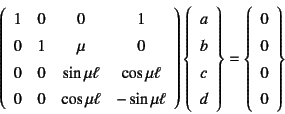
を得る。しかしながら
と一定値をとることからすべての積分定数は零以外にはなり得ず, 結局座屈は発生しないことを結論付ける。
観察とは違う結論になってしまったが,これは梁-柱理論が
そのままでは適用できない不安定現象の例だからである。
詳細については参考文献[73]等を
参照して欲しいが,この問題を解決するには動的に問題を解く必要がある。
この系の固有振動数の最低次からの二つを![]() ,
, ![]() と
記すことにすると,図-6.31に模式的に描いたように,
外力が増えるに従ってこの二つの振動数が近づき,
ある外力レベル
と
記すことにすると,図-6.31に模式的に描いたように,
外力が増えるに従ってこの二つの振動数が近づき,
ある外力レベル![]() で一致する。このレベルを越える外力に
対しては振動数が複素数
で一致する。このレベルを越える外力に
対しては振動数が複素数
![]() に
なるため,解が
に
なるため,解が
となる。これは時間と共に発散する解を含んでおり,
系が動的不安定
になることを意味する。上の柱の場合は
という座屈荷重を持つことがわかっている。
図-6.32に示したような等分布外力が
作用した両端単純支持梁の圧縮を検討する。
この場合は最初から棒が曲がっているので,図-6.7の
実線のように分岐現象は起きず,
![]() になるにつれて
急激にたわみが大きくなることが予想される。
そのつり合い式は式(6.30)より
になるにつれて
急激にたわみが大きくなることが予想される。
そのつり合い式は式(6.30)より
であり,境界条件は両端で![]() ,
, ![]() である。
式(6.33)で定義した
である。
式(6.33)で定義した![]() を
用いると,斉次解は前節と同様になり,
特解が
を
用いると,斉次解は前節と同様になり,
特解が
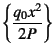 で
あればいいことから,一般解は
で
あればいいことから,一般解は
となる。これを上の両端の境界条件に代入すると,
まず![]() の条件から
の条件から
となり,![]() の条件を加えると
の条件を加えると
となる。したがってたわみは
となり,その2階の微係数から曲げモーメントは
と表現できる。
たわみが最大になるのは![]() を計算するまでもなくスパン中央に
なるので,上式に
を計算するまでもなくスパン中央に
なるので,上式に
![]() を代入すると
を代入すると
となる。右辺括弧内の分母に
![]() という
項があるが,これが零になるのは
という
項があるが,これが零になるのは
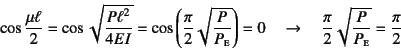
より,![]() を満足するときであることがわかる。
すなわち,例えば等分布外力
を満足するときであることがわかる。
すなわち,例えば等分布外力![]() が一定の
まま軸力
が一定の
まま軸力![]() を増加させていった場合には,その軸力がEuler荷重に
一致したときにたわみが無限大になり,座屈する。
曲げモーメントも同様に,スパン中央で最大になり
を増加させていった場合には,その軸力がEuler荷重に
一致したときにたわみが無限大になり,座屈する。
曲げモーメントも同様に,スパン中央で最大になり
となる。これも
![]() で無限大になる。
このような結果は,前節の剛体バネモデルで比較的小さい変位状態を
考えた場合にも求められている。図-6.33の
破線が上式で示した二つの解であり,図-6.7の
実線とよく似た変化を示している。
この
で無限大になる。
このような結果は,前節の剛体バネモデルで比較的小さい変位状態を
考えた場合にも求められている。図-6.33の
破線が上式で示した二つの解であり,図-6.7の
実線とよく似た変化を示している。
この
![]() が,たわみや曲げモーメント,
ひいては応力の軸力による増幅の影響を代表したものになっており,
剛体バネモデルにおける式(6.16)の,外力による
増幅係数
が,たわみや曲げモーメント,
ひいては応力の軸力による増幅の影響を代表したものになっており,
剛体バネモデルにおける式(6.16)の,外力による
増幅係数![]() と同じ機能を果たしている。
ここではさらに設計の観点からもう少し使い易い表現で近似してみよう。
と同じ機能を果たしている。
ここではさらに設計の観点からもう少し使い易い表現で近似してみよう。
第15版までは,![]() が零に近い範囲の近似を求めるという
頓珍漢なことをしていた。文献[9]をゼミで読んで
その間違いに気付き,それを参考にして書き直しておく。
設計に必要なのは
が零に近い範囲の近似を求めるという
頓珍漢なことをしていた。文献[9]をゼミで読んで
その間違いに気付き,それを参考にして書き直しておく。
設計に必要なのは![]() が座屈荷重に近い範囲での近似解である。
つまり,
が座屈荷重に近い範囲での近似解である。
つまり,
![]() の
近傍でTaylor展開する必要がある。
そこで
の
近傍でTaylor展開する必要がある。
そこで
![]() に
に![]() の定義を
代入し,Euler荷重の表現式(6.35)を用いると,
次のように近似できる。まず
の定義を
代入し,Euler荷重の表現式(6.35)を用いると,
次のように近似できる。まず
となるので,
![]() から
から
![\begin{eqnarray*}
&=&\left(\dfrac{\pi}{2}-\dfrac{\mu\ell}{2}\right)
- O\left\{\...
...ht\}\right]
= \dfrac{\pi}{4}\left(1-\dfrac{P}{P\subsc{e}}\right)
\end{eqnarray*}](s2img791.gif)
と6.8な
る。つまり
となる。
この近似はまさに式(6.16)の![]() の
分母の
の
分母の
![]() 倍になっている。
この近似を用いると最大たわみと最大曲げモーメントは
倍になっている。
この近似を用いると最大たわみと最大曲げモーメントは
| (6.46) |
という表現になる。図-6.33の実線が この二式である。 厳密解との差異はほとんどないことが明らかである。 設計に適用した例は後述する。
次に同じような状況だが,分布外力ではなく
端部に集中外力モーメントが作用
する図-6.34のような場合を解いてみよう。この
場合は,分布外力が無い代わりに境界条件が
で与えられる。
これも同様に微分方程式を解くと,一般解が
になるから,境界条件に代入して整理すると
と求められる。最大値はやはりスパン中央で発生するので,
それを計算すると
となる。前節の等分布外力が作用した場合と同様
分母に
![]() があり,
があり,
![]() で
無限大になることを示している。
で
無限大になることを示している。
たわみの2階の微係数から曲げモーメントの最大値も
となる。ここで,前節で導入した近似と同様,このcosineの
部分を近似表示してしまうと,例えば最大曲げモーメントは
となる。
まさに剛体バネモデルの式(6.16)の![]() その
ものによって表現できている。図-6.35に
以上の結果を表示した。図中の破線は梁-柱としての
厳密な応答,実線が近似した応答である。
その
ものによって表現できている。図-6.35に
以上の結果を表示した。図中の破線は梁-柱としての
厳密な応答,実線が近似した応答である。
最後に,設計で必要となる応力成分を算定しておこう。まず,
式(4.16)が軸力と曲げモーメントの作用下で発生する応力の
一般的な表現である。
したがって,最外縁応力は
となる。
ここに![]() は式(4.15)で
は式(4.15)で
![]() と
定義された断面係数
であり,
と
定義された断面係数
であり,![]() は,断面の中立軸から最も外の縁までの
は,断面の中立軸から最も外の縁までの![]() 方向の距離である。
この式に,前節の最後の結論で求められた
曲げモーメントの表現式(6.47)を代入すると,
曲げと軸力を受ける棒に発生する最大応力は
方向の距離である。
この式に,前節の最後の結論で求められた
曲げモーメントの表現式(6.47)を代入すると,
曲げと軸力を受ける棒に発生する最大応力は
と表すことができる。
右辺第2項には![]() つまり分母に軸力の項があるが,
これが曲げ応力の成分を座屈現象が増幅する係数に相当している。
つまり分母に軸力の項があるが,
これが曲げ応力の成分を座屈現象が増幅する係数に相当している。
特に弾性完全塑性体で材料特性をモデル化すると,この最大応力は
降伏応力
![]() を越えてはいけないから
辺々
を越えてはいけないから
辺々
![]() で割って
で割って
という関係式が求められる。
この式は設計の照査段階で用いられる軸力と曲げを受ける
部材の強度相関式
の基礎になるものである。ここに
と定義したが,前者は全断面が一様に降伏応力になったときの全断面降伏 軸力,後者は最外縁の応力が降伏応力に達した瞬間の初期降伏 曲げモーメントである。
次に図-6.36にあるように,外力を載荷する前に
初期たわみとして![]() が存在していた場合の挙動について検討する。
図では
が存在していた場合の挙動について検討する。
図では![]() をかなり誇張してある。
このときのつり合い式は,この章での誘導を最初からやり直しても
求めることができるが,図-6.21で見たような軸力に
よる付加曲げモーメント効果を考えると
をかなり誇張してある。
このときのつり合い式は,この章での誘導を最初からやり直しても
求めることができるが,図-6.21で見たような軸力に
よる付加曲げモーメント効果を考えると
でいいことは明らかである。簡単のために
初期たわみは
でモデル化できるとする。
これはEuler座屈モードと一致しているから,Euler座屈に
最も悪い影響を及ぼすと考えられる初期不整なので,
ここで用いることにした。
これを上式に代入し,式(6.33)を考慮すれば
がつり合い式で,境界条件は両端で![]() ,
, ![]() である。
である。
この問題の特解が
であることは容易に算定できる。
一般解はこれに斉次解を加えたものとなるが,もし![]() が座屈荷重に
達していないなら
が座屈荷重に
達していないなら
![]() となるので,
斉次解の積分定数を境界条件から決定するとそれはすべて零になる。
したがって解は特解のみで与えられ,上式を
式(6.35)のEuler荷重を用いて書き直すと
となるので,
斉次解の積分定数を境界条件から決定するとそれはすべて零になる。
したがって解は特解のみで与えられ,上式を
式(6.35)のEuler荷重を用いて書き直すと
となる。この2階の微係数を用いると,曲げモーメントも
となる。
最大曲げモーメントはスパン中央で発生するので,
上式に
![]() を代入すると
を代入すると
となるから,式(6.48)と同様に最大応力を
算定すると
と表現できる。この表現と式(6.48)を比較すると
明らかなように,初期たわみが存在する系の問題は,
端部に![]() の外力曲げモーメントが作用している問題と
等価となっている。
この結論も前節の剛体バネモデルにおける結論と同じである。
の外力曲げモーメントが作用している問題と
等価となっている。
この結論も前節の剛体バネモデルにおける結論と同じである。
柱の座屈実験から座屈荷重を算定する方法にSouthwell法
というのがある。これは式(6.50)を用いた方法なのである。
例えば,この式を2回微分して曲率を計算し,
それを
![]() で算定して,項の順番を入れ替えると
で算定して,項の順番を入れ替えると
と表現できることは容易にわかる。
したがって,外力![]() と曲率
と曲率![]() あるいは
軸線から最外縁までの距離
あるいは
軸線から最外縁までの距離![]() を乗じた
曲げひずみ
を乗じた
曲げひずみ
![]() とを測定し,
横軸に
とを測定し,
横軸に![]() を,縦軸に
を,縦軸に![]() をプロットすれば
その直線の傾きが
をプロットすれば
その直線の傾きが![]() であることを,
式(6.51)は示して
いる。図-6.37に示したのは,
アクリルで作成したものさしのような薄板を重りで圧縮し,
重りから軸力を,板の両表面のひずみゲージから
曲げひずみ成分を測定してグラフ化したものである。
インセットの荷重ひずみ曲線では,
初期不整の影響や棒の端部処理の不具合による非理想的な境界条件の影響のために,
理論的な座屈荷重より低い軸力レベルで大きく曲がり
始めているものの,Southwellプロットからはこの程度の簡単な
実験でも
であることを,
式(6.51)は示して
いる。図-6.37に示したのは,
アクリルで作成したものさしのような薄板を重りで圧縮し,
重りから軸力を,板の両表面のひずみゲージから
曲げひずみ成分を測定してグラフ化したものである。
インセットの荷重ひずみ曲線では,
初期不整の影響や棒の端部処理の不具合による非理想的な境界条件の影響のために,
理論的な座屈荷重より低い軸力レベルで大きく曲がり
始めているものの,Southwellプロットからはこの程度の簡単な
実験でも
![]() Nと,1.2%程度の誤差で
座屈荷重を求めることができている。
なお,この実測値は東北大学における
学部の学生実験で実際に得たデータの1例である。
Nと,1.2%程度の誤差で
座屈荷重を求めることができている。
なお,この実測値は東北大学における
学部の学生実験で実際に得たデータの1例である。
柱の弾性座屈時の荷重は式(6.41)で算定できるが,
実際の材料には弾性限界や降伏応力といった弾性的な抵抗の限界が
存在するため,このままでは現実的な限界応力とは言えない。
非弾性の最も簡単な材料モデルに弾・完全塑性体
モデルがあるが,これは図-6.38のような応力ひずみ関係を
有している。
この場合,軸圧縮を受けた柱の軸応力が
![]() で表された
降伏応力
を越えられないので,単純支持棒の限界応力
式(6.36)も
で表された
降伏応力
を越えられないので,単純支持棒の限界応力
式(6.36)も
![]() を越えることはない。
つまり
を越えることはない。
つまり
となるはずである。この両辺を,降伏応力で割ると
と表現できる。ここに
と定義した量は細長比パラメータ
と呼ばれる。この関係式(6.52)を図示したの
が図-6.39の実線である。
図中の実曲線はいわゆるEuler曲線であり,
![]() が1より
小さい領域では意味が無くなるため,点線にしてある。
柱が比較的短く(太く),細長比パラメータが小さい領域では,
限界応力は座屈応力ではなく降伏応力,つまり材料そのものの
一種の強度で与えられることになる。
これが図の水平な実線の部分に相当する。
が1より
小さい領域では意味が無くなるため,点線にしてある。
柱が比較的短く(太く),細長比パラメータが小さい領域では,
限界応力は座屈応力ではなく降伏応力,つまり材料そのものの
一種の強度で与えられることになる。
これが図の水平な実線の部分に相当する。
しかし,例えば高張力鋼等の応力ひずみ曲線を見ると, 弾・完全塑性体モデルでは表しきれない ような非線形の部分が存在することがある。 また塑性においては,載荷と除荷では その経路が異なるのが普通である。そこで,まず 簡単な材料モデルとして図-6.40にあるような 非線形弾性体 を考え,それでできた柱の座屈公式を検討する。 ただしこの材料は,図にも示したように載荷と除荷 の経路が同じ弾性モデルである。
剛体バネモデルの節で見たように安定問題の取り扱い方には,
近似の無い有限変位理論を用いること以外に,
式(6.5)で見たように,あるつり合い位置からの
増分理論として問題を捉える方法があった。
したがって,材料の性質が非線形になった場合には,ここで
用いている比較的小さい変位で表した理論を,座屈が発生する
瞬間の増分応力と増分ひずみとの関係に基づいたものに
読み換えればいい。
すなわち,この節で用いている弾性のYoung率![]() の代わりに,
座屈する瞬間の増分Young率あるいは接線Young率
の代わりに,
座屈する瞬間の増分Young率あるいは接線Young率![]() を
使えば正しい座屈応力を算定できそうだ。
したがって,ここで考えているような非線形弾性体でできた柱の
座屈応力は
を
使えば正しい座屈応力を算定できそうだ。
したがって,ここで考えているような非線形弾性体でできた柱の
座屈応力は
となる。すなわち係数
![]() が非線形性の影響を
代表しており,接線Young率を用いることから接線係数理論
と呼んでいる。
この影響を模式的に示したのが図-6.39の
破線である。ここでは図-6.40にもある
ように,
が非線形性の影響を
代表しており,接線Young率を用いることから接線係数理論
と呼んでいる。
この影響を模式的に示したのが図-6.39の
破線である。ここでは図-6.40にもある
ように,
![]() を降伏応力ではなく,応力の
上限値である終局応力のような
ものでモデル化してあることに注意する。
接線Young率
を降伏応力ではなく,応力の
上限値である終局応力のような
ものでモデル化してあることに注意する。
接線Young率![]() が初期のYoung率
が初期のYoung率![]() よりも小さくなる
ため,普通のEuler曲線および
よりも小さくなる
ため,普通のEuler曲線および
![]() レベルより
も小さめの値を示している。
レベルより
も小さめの値を示している。
前節の非線形弾性体は,本当は非常に限られた材料が示す特性であり, 多くの材料は塑性 と呼ばれる非可逆特性を有しているのが普通である。 その特徴を簡単に示したのが図-6.41である。 最も特徴的なのは,載荷経路と除荷経路が異なっている点である。 ただし,たいていのモデルでは,これも図示したように, 除荷の抵抗係数を弾性係数と同じにしている。
さて,剛体バネモデルに対する定式化でも示したように, 安定問題の検討では,あるつり合い状態を 与える外力条件が不変なままで 複数のつり合い状態が可能になる点を探している。 ここでも,加えた軸力は不変のままで曲がる条件を探さなければならない。 しかし弾塑性材料では,図-6.41のように 載荷される部分と除荷される部分の接線抵抗係数が違う。 そのため,座屈して断面内のひずみが一様でなくなるとき, 載荷域と除荷域の領域の拡り方が同じだと軸力が変化することになる。 したがって,軸力が変化しないように, 載荷域と除荷域の領域の拡り方には違いが生じなければならない。 つまり,作用している軸力が座屈前後で不変なまま付加的な曲げ変形が 発生するためには,図-6.42に示したように 増分ひずみが変化しなければならないのである。
例えばこの図-6.42が矩形断面の場合の応力分布だとすると,
右端に示した座屈の瞬間の
応力分布のうちの,(c, d, e)で囲まれた三角形の面積(増分載荷応力の総和)
が(e, f, g)で囲まれた三角形の面積(増分除荷応力の総和)と
等しくなるように,増分ひずみは直線分布しなければならないことになる。
したがって,右から二番目の図の直線分布(a, b)のように,
増分ひずみについての中立軸は図心からずれることになる。
このような考察で座屈応力を求めると
となる。この公式は換算係数理論
による座屈応力と呼ばれ,![]() はKármánによる換算係数と
呼ばれている。この係数は断面形状と
はKármánによる換算係数と
呼ばれている。この係数は断面形状と![]() と
と![]() の
関数になるが,例えば長方形断面の場合には
の
関数になるが,例えば長方形断面の場合には
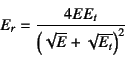
という関係になる。
このようにして求められる非弾性座屈公式(6.54)や式(6.55)と,
いわゆるEuler座屈公式とを比較すれば明らかなように,
どの公式もその表現は同じである。
当然![]() であることから,三つの係数の大小関係は
であることから,三つの係数の大小関係は
となっているため,前節の接線係数理論の座屈応力と合わせて示すと
という大小関係になる。
以上のように,載荷域と除荷域を区別して求められる換算係数理論は, 接線係数理論よりも力学的には合理的に見える。しかしながら, 弾塑性体の座屈を取り扱う場合には,外力が不変のままの乱れを考えるのが 不適当であるという結論を,Shanley[66]は簡単なモデル を用いて示した。 すなわち実際の現象では,接線係数理論で求められる 応力レベルで分岐現象が可能となるが,そのレベルと 換算係数理論による応力レベルの中間レベルで,外力が 増加しながら曲げ変形が増大すると考えられている。 したがって,設計等で弾塑性の影響を考慮して座屈応力を 算定する場合には,安全側でもあることから接線係数理論に よる応力が用いられる。その他の塑性座屈等については 文献[36]等を参照のこと。 実際には,柱そのものが予め曲がっていることや 溶接部に分布する残留応力等の種々の初期不整 の影響で, ここで得た座屈応力よりさらに低い応力レベルで変形が大きくなり始める。 したがって,設計に用いる公式等にはこのような複雑な 影響を取り入れてあり,より安全側の評価ができるようになっている。
初期不整の一つである残留応力の影響についても例を示しておこう。 鋼構造のように圧延 で造られた部材や,その薄板を溶接 して部材にした場合の接合部等には残留応力 が存在する。 ここでは最も基本的な例として,圧延I形断面の場合の残留応力の 影響について概説する。 計算法については文献[133]等に詳細が示されているので, ここには結果のみを図示しておく。
材料は弾・完全塑性体で,図-6.43の左図に
あるようなパターンの残留応力がフランジ部に存在するものと
する。
![]() は降伏応力である。
細長比パラメータと座屈応力の関係が同じ図の右側に示してある。
ここに
は降伏応力である。
細長比パラメータと座屈応力の関係が同じ図の右側に示してある。
ここに
![]() は強軸曲げに関する細長比
パラメータであり,
は強軸曲げに関する細長比
パラメータであり,
![]() は弱軸に関する
ものである。二つの曲線はそれぞれの軸に関する曲げ座屈応力を
表し,曲げを受けている面を下添え字で区別してある。
残留応力の存在によって弾・完全塑性体の
座屈曲線図-6.39よりさらに下方に座屈強度が
落ちている。
その他の残留応力分布に対する座屈曲線等についても,別途
参考文献等を参照して欲しいが,
残留応力は断面形状や残留の原因に依存してその分布が異なるため,
実際の設計に用いられる座屈曲線は断面形状によっても
分類されている。
は弱軸に関する
ものである。二つの曲線はそれぞれの軸に関する曲げ座屈応力を
表し,曲げを受けている面を下添え字で区別してある。
残留応力の存在によって弾・完全塑性体の
座屈曲線図-6.39よりさらに下方に座屈強度が
落ちている。
その他の残留応力分布に対する座屈曲線等についても,別途
参考文献等を参照して欲しいが,
残留応力は断面形状や残留の原因に依存してその分布が異なるため,
実際の設計に用いられる座屈曲線は断面形状によっても
分類されている。
このように,1軸状態にある材料の強度は引張りと圧縮で異なる。
引張り状態では,材料そのものの強度を構造部材の強度に直接関連付けていいから,
許容応力設計法の考え方では,
降伏応力を用いて引張り許容応力
![]() (引張り強度
)は
(引張り強度
)は
で与えられる。ここに![]() は安全率
と呼ばれる係数で,現在の構造材料では通常1.7程度の値をとる。
安全率は,荷重や構造あるいは解析における不確実さや誤差を
考慮するための余裕の係数である。
これに対し,圧縮許容応力
は安全率
と呼ばれる係数で,現在の構造材料では通常1.7程度の値をとる。
安全率は,荷重や構造あるいは解析における不確実さや誤差を
考慮するための余裕の係数である。
これに対し,圧縮許容応力
![]() (圧縮強度
)は座屈強度で定義され,引張り同様の安全率を用いて
(圧縮強度
)は座屈強度で定義され,引張り同様の安全率を用いて
のように規定[128]されている。図-6.44に その関数をEuler曲線と比較して描いた。
弾性の梁-柱理論は見かけ上
線形理論なので,章-5で用いた手法を
そのまま使って要素剛性方程式を求めることができるはずだ。
変位で表したつり合い式が式(6.30)だから,
まず弱形式の最初の段階が
と書くことができる。被積分関数の第1, 2項についてそれぞれ2回
あるいは1回
部分積分して整理し,式(6.31)で与えられる
境界条件を代入すると,仮想仕事式
が
となる。章-5で
扱った初等梁理論のそれと異なるのは第2項のみである。
用いる変位関数は,その条件が初等梁理論と同じなので同じ関数で
いい。したがって,式(5.20)を上の
式の第2項に代入すると![]() に比例した剛性行列
が新たに追加されて,剛性方程式は
に比例した剛性行列
が新たに追加されて,剛性方程式は
となる。
ここに![]() 以外はすべて章-5で定義されている。
この
以外はすべて章-5で定義されている。
この![]() は幾何剛性行列
と呼ばれるもので,
式(5.20)第2項より
は幾何剛性行列
と呼ばれるもので,
式(5.20)第2項より
で定義される。具体的に関数を代入して積分を実行すると
という値を持つ。 幾何剛性という名称は,この安定問題を考えるに当たって 変位したあとの幾何形状でつり合いを考えることが重要だったことに由来している。
式(6.58)を用いて,例えば両端単純支持棒の座屈荷重を
計算してみよう。まずこの要素剛性方程式を一つだけ用い,全長を一つの
有限要素として解いてみる。
上の剛性方程式に両端の境界条件を代入すると,
結局,まず解くべき式は剛性方程式の第2, 4行目だけになる。
つまり
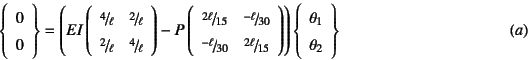
を満足するようにたわみ角![]() と
と![]() を求めればいい。
しかし左辺が零ベクトル(広義で)であるから,もし右辺の係数行列が
正則なら逆行列が存在し,その結果たわみ角は零となり座屈しない。
あるいは,それは座屈する前の答と考えればいい。
したがって逆に,この係数行列が特異になるときに座屈が発生すると考えていいから,
この係数行列の行列式を零にする条件から座屈荷重が決定できる。
つまり,剛性方程式の解が零ベクトルにならない,
あるいは無意味な解
を持たない条件から,剛性行列の固有値問題
として座屈問題が記述される。すなわち,この場合には
を求めればいい。
しかし左辺が零ベクトル(広義で)であるから,もし右辺の係数行列が
正則なら逆行列が存在し,その結果たわみ角は零となり座屈しない。
あるいは,それは座屈する前の答と考えればいい。
したがって逆に,この係数行列が特異になるときに座屈が発生すると考えていいから,
この係数行列の行列式を零にする条件から座屈荷重が決定できる。
つまり,剛性方程式の解が零ベクトルにならない,
あるいは無意味な解
を持たない条件から,剛性行列の固有値問題
として座屈問題が記述される。すなわち,この場合には
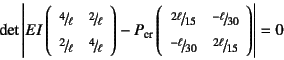
となる。ここで
![]() と
定義すると,この行列式は
と
定義すると,この行列式は
となる。したがって
と座屈荷重の近似値が求められる。式(6.34)から,第1次と
第2次の座屈荷重はそれぞれ
であったことを用いれば,上の解の誤差はそれぞれ
![]() %,
%,
![]() %の
過大評価であることを示している。
%の
過大評価であることを示している。
もちろん梁-柱理論の
たわみの一般解にはsine, cosineが含まれており,
有限要素近似の変位関数として
選んだ多項式が厳密解ではない以上,このような近似解しか
求められないのは当然である。有限要素法は,要素の数を増やしたときに
その近似解が厳密解に収束することを保証しているに過ぎない。
したがって精度のいい座屈荷重を求めるためには,やはり対象を
複数の有限要素に分割して近似度を上げる必要が
ある。表-6.1にその結果を示した。
ただし![]() は
は![]() 次の座屈荷重の有限要素解と厳密解の
比であり
次の座屈荷重の有限要素解と厳密解の
比であり
と置いた。 表の1行目は上の計算の結果であり,2行目は要素を二つにして4自由度 として計算したものである。2要素だけでも, 工学的に最も重要な最低次の座屈荷重が誤差0.8%程度になっている。 近似解が厳密解より大きくなるのは,近似することによってモデルの 変形が真の変形より拘束されたものになる等,その剛性が大きく なるからである。これは表-5.3で示した 有限要素法による固有振動数の近似解が持つ特徴(厳密解より高めの 振動数になること)と同じである。
ここでは比較的小さい変位の範囲での梁-柱理論を
元にしているから,式(6.58)の剛性行列は軸力![]() が
作用した構造系の接線剛性と考えていい。
式(6.13)では接線剛性の正負によっても
系の安定不安定を判定できることを示した。
この節の剛性行列でも同じ判定ができるはずだ。
例えば1要素で解いた場合の式(
が
作用した構造系の接線剛性と考えていい。
式(6.13)では接線剛性の正負によっても
系の安定不安定を判定できることを示した。
この節の剛性行列でも同じ判定ができるはずだ。
例えば1要素で解いた場合の式(![]() )を見てみよう。
式(6.13)と異なり,この場合の接線係数は
行列になっている。
したがって「係数の正値性」は「係数行列の正値性」と
読み替えなければならず,結局その安定条件は
)を見てみよう。
式(6.13)と異なり,この場合の接線係数は
行列になっている。
したがって「係数の正値性」は「係数行列の正値性」と
読み替えなければならず,結局その安定条件は
でなければならない。したがってこの例では
となる。後者は式(![]() )からの結論に対応していて,
前者は接線係数行列の第1行第1列の正値条件である。
この二つの条件から,
)からの結論に対応していて,
前者は接線係数行列の第1行第1列の正値条件である。
この二つの条件から,![]() においてのみ系は安定であるとわかり,
第1次の近似座屈荷重がこの近似した系の不安定発生点であることが
わかる。
この係数行列の正値性による安定判定は,
安定なHookeの弾性体が持つべきPoisson比の範囲を求めるときの
式(3.48)でも用いた。
別の見方をすると次のようなことが成り立つ。
ある与えられた
においてのみ系は安定であるとわかり,
第1次の近似座屈荷重がこの近似した系の不安定発生点であることが
わかる。
この係数行列の正値性による安定判定は,
安定なHookeの弾性体が持つべきPoisson比の範囲を求めるときの
式(3.48)でも用いた。
別の見方をすると次のようなことが成り立つ。
ある与えられた![]() に対する式(
に対する式(![]() )の「接線」係数行列6.9の
固有値(
)の「接線」係数行列6.9の
固有値(![]() ではなく,
ではなく,![]() を固有ベクトルをとして
境界条件を代入した全体剛性を用いた
を固有ベクトルをとして
境界条件を代入した全体剛性を用いた
![]() で,「接線」行列
で,「接線」行列
![]() の固有値
の固有値![]() のこと)は,
系が安定な場合にはすべてが正である。
しかし,最初の分岐点で最小固有値が零になり,
そのあと
のこと)は,
系が安定な場合にはすべてが正である。
しかし,最初の分岐点で最小固有値が零になり,
そのあと![]() を増加させていくと
固有値
を増加させていくと
固有値![]() の小さい方から順に負になっていくことになる。
の小さい方から順に負になっていくことになる。