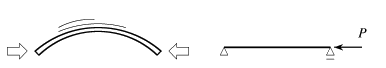最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。

6.1 安定問題とは

図 6.1: 細長い棒を押して曲げる

安定問題が何なのか既に知っている読者は節-6.4から。 さて，例えばプラスティック製30cmものさしを引張って 壊そうとしても普通は無理そうだが， 押すと図-6.1の左図のように 簡単に曲がって壊れそうになる。 しかも，両端を握って単に曲げるのと両方から 押して曲げるのとを比べると，なんとなく 後者の方が小さい力で「突然」大きく曲がるように感じないだろうか。 ところが， 図心にこのような圧縮外力を作用させる限りは， ものさしを押すという軸の伸び縮みに関するつり合い式と， 実際に発生する曲げに関するつり合い式とが独立になることを， 式(4.27)は示している。 ということは， ものさしを押すときの境界条件は図-6.1の右に示した ような状態なので，曲がらないように注意深く図心の箇所を押す限り， 解は単に縮むだけのはずである。しかし実際には簡単に曲がって しまう。なぜだろう? それは，実際には図心を正確に押すことができないからだという人もいるだろう。 しかし，もし図心から$e$だけずれた箇所を押した 場合には，章-4の図-4.23の ように$C_2=e P$の集中外力モーメントが作用したのと同じだから， たわみは単に$P$に比例するだけだ。 したがって「突然」大きく曲がるといったことはやはり起きないことになる。

図 6.2: 変位した棒の微分要素に働く内力

もしかすると章-4で誘導した初等梁理論は 間違っているんじゃないだろうか。 誘導過程で何か間違いをしていないだろうか。 例えば，軸力やせん断力と曲げモーメントが発生してつり合っている 状態を示した図-4.6を見てみよう。 構造部材は変形して抵抗する物体として定義していたにもかかわらず， この図の微分要素は変形しておらず，変位前の状態のままで力のつり合いを 考えていることに気が付く。本当なら図-6.2のように， 微分要素が変位して変形した状態で力はつり合っていなければ ならないはずだ。 もしかすると上のものさしの問題は，実際に変位した状態でつり合いを 考えて修正すれば解決できるのかもしれない。 すなわち，たとえ図心に圧縮力だけが作用していた場合であっても， それが曲がった状態で つり合う可能性を章-4では検討していなかったのでは ないだろうか。

構造力学の対象は通常，航空機や船体・橋梁・建築物・杭等であり， 使用中の実際の構造物全体を観たときに， 目に見えるくらいの大きさの変位が生じることは少ない。 いや，橋を歩いて渡っているときにトラックが通ると，かなり揺れていると 感じるという人もいるかもしれない。しかし，実際に揺れの 振幅を測定すると，橋の長さに比べれば無視できるくらい非常に小さい。 実は体は加速度を感じるので，大きく揺れているように思ってしまうだけなのである。 したがって，変位する前の状態でつり合いを考えて 定式化した章-4の 理論で設計しても十分な安全を確保できると考えられ，またその方が簡便である。 このような理論を， 変位が非常に小さい範囲での理論であることから微小変位理論 と呼んでいる。 これは未知関数等の線形項のみを取り出して定式化されて おり，線形理論の範疇に入る。 しかし上述の30cmものさしの例でもわかるように，現実の構造部材であっても， この微小変位理論の枠の中では予測できない現象がありそうだ。 微小でない変位状態を考える理論を有限変位理論 と総称^6.1している。 こういった理論は非線形理論になる。

線形理論の範囲内なら，ものさしは圧縮に対して単純に縮むだけである。 しかし圧縮力がある値に到達したとき，この縮むだけのつり合い状態が 安定ではなくなり，それ以外の状態，つまり曲がった状態に移行している とは考えられないだろうか。 このような現象を扱う問題を安定問題 と称している。 棒の安定問題を解析するためには，圧縮された棒が曲がった状態でつり合う 可能性があるか否か検討する必要があり，上述の有限変位理論を 定式化する必要が出てくる。 ただ鋼構造物の実際の不安定現象等を念頭に置き，変位は比較的大きいが 変形（ひずみ）そのものは小さく，材料はほとんど弾性域に あるものとして，この章では主に弾性安定を対象とする。

最新版を正確に読むためには pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。