 |
最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
棒の安定問題を議論する前に,安定問題を数理的にはどのように取り扱う
ことができるかについて,簡単な剛体バネモデル6.2で考えて
おこう。図-6.3に示したように剛棒が回転自由な
支持条件で壁に取り付けてあり,それが線形の回転バネで支持されているとする。
回転バネ6.3は棒の回転角度に
比例したモーメント反力を発生するバネで,その比例係数を![]() とする。
重力は無視し,バネの自然状態で剛棒は水平になっているものとする。
ここでは,2種類の外力
とする。
重力は無視し,バネの自然状態で剛棒は水平になっているものとする。
ここでは,2種類の外力![]() および
および![]() が作用した系が安定か否か検討する。
安定性の確認のためなので,上述のように,
系が変位した状態でのつり合いを考える必要がある。
つまり,図のように水平状態から時計回りに
が作用した系が安定か否か検討する。
安定性の確認のためなので,上述のように,
系が変位した状態でのつり合いを考える必要がある。
つまり,図のように水平状態から時計回りに![]() だけ回転した状態で
支持点A回りの反時計回りのモーメントのつり合いをとる必要があり,それは
だけ回転した状態で
支持点A回りの反時計回りのモーメントのつり合いをとる必要があり,それは
となる。![]() が作用していないとき
が作用していないとき![]() が上式を満足するのは
明らかである。つまり,
が上式を満足するのは
明らかである。つまり,![]() の作用だけならこの棒は回転せずに
いられることを示しているが,前述の30cmものさしの場合と同様,
直感的にはそれが不自然にも感じられる。
の作用だけならこの棒は回転せずに
いられることを示しているが,前述の30cmものさしの場合と同様,
直感的にはそれが不自然にも感じられる。![]() 以外の可能性は無いだろうか。
以外の可能性は無いだろうか。
まず![]() の場合には,つり合い式が
の場合には,つり合い式が
であることから,![]() の状態があり得るとすると,
外力と回転角の関係は
の状態があり得るとすると,
外力と回転角の関係は
となる。この式を図示するのは容易であるが,例えば![]() の
極限で右側の式の右辺は1になる。すなわち,ここで
考えているモデルは外力
の
極限で右側の式の右辺は1になる。すなわち,ここで
考えているモデルは外力![]() が
が
で定義される値を持っていても回転せず,![]() のままで
いられることを示している。
そこで,
のままで
いられることを示している。
そこで,![]() の範囲で式(6.3)を
満足する
の範囲で式(6.3)を
満足する![]() の
の![]() と
と![]() の関係を計算して
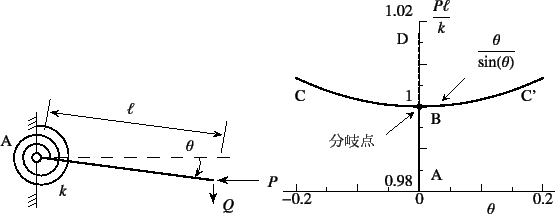
図示すると,図-6.4のB
の関係を計算して
図示すると,図-6.4のB![]() C, B
C, B![]() C'の太い曲線の
経路になる。
つまり,式(6.3)の
C'の太い曲線の
経路になる。
つまり,式(6.3)の![]() の
範囲においては
の
範囲においては![]() のつり合い状態が存在することを示している。
もちろん元の式(6.2)は,
のつり合い状態が存在することを示している。
もちろん元の式(6.2)は,![]() がどんな
値であろうと
がどんな
値であろうと![]() がつり合い状態の解であることを示しているから,
同じ図のAからDまでのような経路も正しいつり合い状態である。
がつり合い状態の解であることを示しているから,
同じ図のAからDまでのような経路も正しいつり合い状態である。
以上の結果をまとめると,この系のつり合い状態は
ことを示している。
このように,式(6.4)で定義された外力レベルは,
複数のつり合い経路に枝分かれする限界点であることから分岐点
と呼ばれており,
式(6.4)の値![]() を分岐荷重
と呼んでいる。
一種の限界荷重なので添え字に`cr(itical)'と書いてあることが多い。
あるいは,節-6.3で例示するように,
構造部材の同様の不安定現象を座屈と呼ぶので,
この分岐荷重のことを座屈荷重
と呼ぶこともある。
を分岐荷重
と呼んでいる。
一種の限界荷重なので添え字に`cr(itical)'と書いてあることが多い。
あるいは,節-6.3で例示するように,
構造部材の同様の不安定現象を座屈と呼ぶので,
この分岐荷重のことを座屈荷重
と呼ぶこともある。
では外力を![]() よりも大きくしたとき,自然は
この三つのつり合い状態のうちのどのつり合い経路を
選ぶだろうか。
もし三つの状態共に安定であれば,自然がどのつり合い状態を
選ぶかについては確率論的なことになるかもしれないし,あるいは別に
例えばエネルギ的な力学規準に即して,ある一つのつり合い状態を
選ぶかもしれない。
しかし,もしいずれかが不安定な状態であれば,
その状態を自然界では保持できず,現実にはほとんど起こり得ないかもしれない。
したがって,自然界での系の挙動を予測するためには,少なくとも
つり合い状態が安定か否かについては検討する必要があり,そのための
何らかの判定規準が別途必要になる。
よりも大きくしたとき,自然は
この三つのつり合い状態のうちのどのつり合い経路を
選ぶだろうか。
もし三つの状態共に安定であれば,自然がどのつり合い状態を
選ぶかについては確率論的なことになるかもしれないし,あるいは別に
例えばエネルギ的な力学規準に即して,ある一つのつり合い状態を
選ぶかもしれない。
しかし,もしいずれかが不安定な状態であれば,
その状態を自然界では保持できず,現実にはほとんど起こり得ないかもしれない。
したがって,自然界での系の挙動を予測するためには,少なくとも
つり合い状態が安定か否かについては検討する必要があり,そのための
何らかの判定規準が別途必要になる。
そこで,つり合っている系を少しだけ
乱したときの応答を算定してみよう。
このバネモデルのあるつり合い状態を![]() とすると,
それは式(6.1)から点A回りのモーメントの総和が
零,つまり
とすると,
それは式(6.1)から点A回りのモーメントの総和が
零,つまり
を満足している。
ここで外力は変えずに回転角を少しだけ乱して,
時計回りに増えて
![]() になったとすると,
モーメントの総和は
になったとすると,
モーメントの総和は
となるが,![]() は非常に小さく
は非常に小さく
![]() で
あることを考慮すれば
で
あることを考慮すれば
と近似できるので,![]() が上のつり合い式を満足していることを
用いると,上式は
が上のつり合い式を満足していることを
用いると,上式は
となる。
外力![]() と
と![]() とは変化させていないから
とは変化させていないから![]() は
系全体の反時計回りのモーメント抵抗力の乱れ
であり,
は
系全体の反時計回りのモーメント抵抗力の乱れ
であり,![]() は逆に時計回りの乱れ回転角を正にとっていた。
時計回りに強制的に乱れを起こそうとしたとき,もし反時計回りの
抵抗力が正であれば系が乱れに抵抗しようとしていることになり,
その乱れを加える前のつり合い状態に戻ろうとするだろう。
つまり,そのつり合い状態は安定ということになるだろう。
すなわち,式(6.5)の右辺が正の
は逆に時計回りの乱れ回転角を正にとっていた。
時計回りに強制的に乱れを起こそうとしたとき,もし反時計回りの
抵抗力が正であれば系が乱れに抵抗しようとしていることになり,
その乱れを加える前のつり合い状態に戻ろうとするだろう。
つまり,そのつり合い状態は安定ということになるだろう。
すなわち,式(6.5)の右辺が正の![]() に
対して正であれば安定である。したがって
に
対して正であれば安定である。したがって
であれば安定ということになる。
あるいは,動的に考えるともっと理解し易いかもしれない。
つまり,あるつり合い状態を少しだけ
動的に乱したときの乱れ
![]() が,時間とともに
発散しようとするのか,減衰あるいは振動しようとするのか判定すれば,
その状態が安定か否かの判断ができるのではないだろうか。
そこで,この系の運動方程式を求めてみよう。式(6.5)は
反時計回りのモーメントであり,
が,時間とともに
発散しようとするのか,減衰あるいは振動しようとするのか判定すれば,
その状態が安定か否かの判断ができるのではないだろうか。
そこで,この系の運動方程式を求めてみよう。式(6.5)は
反時計回りのモーメントであり,![]() は時計回りの
回転角だったから,この剛棒の回転慣性を
は時計回りの
回転角だったから,この剛棒の回転慣性を![]() とすると,
乱れの動的な運動は時計回りのモーメントの運動方程式
とすると,
乱れの動的な運動は時計回りのモーメントの運動方程式
で支配される。ここに,![]() は時間に関する2階の
微係数を表している。
この運動方程式の解の性質について検討すると,
は時間に関する2階の
微係数を表している。
この運動方程式の解の性質について検討すると,![]() なので次のようなことになる。
なので次のようなことになる。
となる。これは乱れが時間と共に発散することを示しており, 不安定な状態を意味する。
となり,乱れは振動解である。ここでは減衰の効果を含めて いないので,乱れが振動解になる場合には安定と考えていい。
したがって,この系が安定であるための条件は左辺の括弧内が 正であることであり,それは式(6.6)の安定規準と同じである。
まず,横荷重が無い![]() の場合を検討すると,安定規準式(6.6)は
の場合を検討すると,安定規準式(6.6)は
となる。すると,![]() のまっすぐな状態は,
この安定規準式(6.6)から
のまっすぐな状態は,
この安定規準式(6.6)から![]() の場合
つまり
の場合
つまり![]() においてのみ安定であることがわかる。
したがって,図-6.4のA
においてのみ安定であることがわかる。
したがって,図-6.4のA![]() Bは安定な
つり合い経路であるが,B
Bは安定な
つり合い経路であるが,B![]() Dのつり合い経路は不安定で自然界では
観測され難いことになる。
もし
Dのつり合い経路は不安定で自然界では
観測され難いことになる。
もし![]() が一定の場合には,
が一定の場合には,![]() はつり合い式
はつり合い式
を満足するので,これを式(6.6)に
代入すると,つり合っている系の回転角![]() で
表した安定規準は
で
表した安定規準は
とも表すことができる。分岐したあとの経路B![]() C, B
C, B![]() C'が安定か
どうかについては,次節で示す。
C'が安定か
どうかについては,次節で示す。
安定規準をもう少し違うアプローチから検討してみよう。簡単のために,
最初は外力![]() が無い場合を取り扱う。章-5では
線形理論の弱形式から
全ポテンシャルエネルギというスカラー量を誘導し,
つり合い状態はその全ポテンシャルエネルギが最小になる
状態に相当することを示した。
したがって,つり合っている状態の外力を変えずに強制的にさらに
変形させようとすると,全ポテンシャルエネルギは増加する。
しかし,その系がつり合おうとするときには全ポテンシャルエネルギが
小さくなるような運動をするため,元のつり合い点すなわち
その外力レベルにおける唯一のつり合い点に戻る運動をする。
つまり,全ポテンシャルエネルギを最小にするつり合い状態は
安定であると判断できる。
が無い場合を取り扱う。章-5では
線形理論の弱形式から
全ポテンシャルエネルギというスカラー量を誘導し,
つり合い状態はその全ポテンシャルエネルギが最小になる
状態に相当することを示した。
したがって,つり合っている状態の外力を変えずに強制的にさらに
変形させようとすると,全ポテンシャルエネルギは増加する。
しかし,その系がつり合おうとするときには全ポテンシャルエネルギが
小さくなるような運動をするため,元のつり合い点すなわち
その外力レベルにおける唯一のつり合い点に戻る運動をする。
つまり,全ポテンシャルエネルギを最小にするつり合い状態は
安定であると判断できる。
このように考えると,複数のつり合い状態が存在する場合には
その個々のつり合い状態における
全ポテンシャルエネルギを算定し,それが最小になる場合のみが
安定なつり合い状態だと判定できる。
式(6.2)から全ポテンシャルエネルギ![]() を
算定するために,この式がその仮想仕事式,つまり第1変分であると置き
を
算定するために,この式がその仮想仕事式,つまり第1変分であると置き
と表示しておく。これを![]() について積分すると
について積分すると
によって全ポテンシャルエネルギを定義できる。
後者の方が![]() がする外力仕事との関係で物理的にはわかり易いが,
同じ
がする外力仕事との関係で物理的にはわかり易いが,
同じ![]() に対するポテンシャルの原点が違うだけなので,以下では前者を用いる。
一方,
上式の第1変分
に対するポテンシャルの原点が違うだけなので,以下では前者を用いる。
一方,
上式の第1変分![]() をさらに
をさらに![]() で微分(変分)することにより,
第2変分(2階の微係数に相当する)は
で微分(変分)することにより,
第2変分(2階の微係数に相当する)は
となる。あるつり合い状態が全ポテンシャルエネルギの
最小原理として認識されるためには,汎関数![]() は,そのつり合い状態で
最小値を持つ下に凸な曲面になっていなければならない。章-5でも
使ったが,曲面が上に凸なのか下に凸なのか調べるには,高校で習った
関数のグラフと微係数との関係から類推されるように,もう一度微分(この
場合は変分)してみてその符号の正負を調べれば
いいことが直感的に理解できよう。
つまりこの第2変分が正である条件
は,そのつり合い状態で
最小値を持つ下に凸な曲面になっていなければならない。章-5でも
使ったが,曲面が上に凸なのか下に凸なのか調べるには,高校で習った
関数のグラフと微係数との関係から類推されるように,もう一度微分(この
場合は変分)してみてその符号の正負を調べれば
いいことが直感的に理解できよう。
つまりこの第2変分が正である条件
を満足するつり合い状態は安定と判断できることになる。
この式は前に得た
安定規準式(6.6)に![]() を代入したものと一致する。
を代入したものと一致する。
試しに![]() ,つまり回転していないつり合い状態を
この式(6.11)に代入すると
,つまり回転していないつり合い状態を
この式(6.11)に代入すると
となり,![]() のまっすぐな状態は
のまっすぐな状態は![]() の場合のみが
安定であり,前節の結論と一致する。
ということは,つまり,分岐条件
は
の場合のみが
安定であり,前節の結論と一致する。
ということは,つまり,分岐条件
は
![]() からも求められることがわかる。
すなわち図-6.4の中の点Bが分岐点で
あり,B
からも求められることがわかる。
すなわち図-6.4の中の点Bが分岐点で
あり,B![]() Dは全ポテンシャル
エネルギが上に凸であるようなつり合い経路になっていて,
不安定な状態になっている。
以上の結果をまとめたのが図-6.5である。
Dは全ポテンシャル
エネルギが上に凸であるようなつり合い経路になっていて,
不安定な状態になっている。
以上の結果をまとめたのが図-6.5である。
図中の一点鎖線が,![]() のときの安定規準式(6.11)を
示している。グラフ上で,この線より上方は
のときの安定規準式(6.11)を
示している。グラフ上で,この線より上方は![]() となる
不安定な領域,下方が
となる
不安定な領域,下方が![]() となる安定領域になっている。
つり合い経路は図-6.4と同様,
この図の太い実線と点線である。
となる安定領域になっている。
つり合い経路は図-6.4と同様,
この図の太い実線と点線である。![]() の
の![]() という
つり合い解が点線で示されているが,このつり合い状態は第2変分が
負の領域にあり,全ポテンシャルエネルギが最大になるつり合い
状態なので不安定である。
一方,
という
つり合い解が点線で示されているが,このつり合い状態は第2変分が
負の領域にあり,全ポテンシャルエネルギが最大になるつり合い
状態なので不安定である。
一方,![]() のつり合い状態は一点鎖線よりも下方にあるため,
安定である。
すなわち,このモデルの外力を零から増やしていくと,
外力が
のつり合い状態は一点鎖線よりも下方にあるため,
安定である。
すなわち,このモデルの外力を零から増やしていくと,
外力が![]() に至るまでは
に至るまでは![]() のまっすぐな状態が
唯一のつり合い状態でかつ安定である。そして,
のまっすぐな状態が
唯一のつり合い状態でかつ安定である。そして,
![]() を
満足する
を
満足する![]() で分岐が可能になる。
さらに外力を増加させて
で分岐が可能になる。
さらに外力を増加させて![]() になると,
回転した状態の方が安定なので,どちらかの方向に回転して静止する。
しかし回転の方向は決定できない。
になると,
回転した状態の方が安定なので,どちらかの方向に回転して静止する。
しかし回転の方向は決定できない。
同じ図-6.5の右側に,式(6.9)で
計算した全ポテンシャルエネルギの分布状況をそれぞれの
外力レベルで示しておいた。
一番下の
![]() での分布図から,
での分布図から,![]() が
唯一の安定なつり合い状態であることがわかる。
その上の図が
が
唯一の安定なつり合い状態であることがわかる。
その上の図が![]() になった瞬間で,第2変分が零になるので
かなりフラットな曲線になっているが,
下にやや凸のポテンシャルエネルギ分布をしている。
さらに外力レベルが上がり,
になった瞬間で,第2変分が零になるので
かなりフラットな曲線になっているが,
下にやや凸のポテンシャルエネルギ分布をしている。
さらに外力レベルが上がり,
![]() に
なると,一番上の図のように
に
なると,一番上の図のように![]() のつり合い状態が
全ポテンシャルエネルギ最大点であるのに対し,
のつり合い状態が
全ポテンシャルエネルギ最大点であるのに対し,![]() の二つの解は
全ポテンシャルエネルギ最小点に相当した安定なつり合い状態であることが
明確である。
の二つの解は
全ポテンシャルエネルギ最小点に相当した安定なつり合い状態であることが
明確である。
一番最初の図-6.3の問題に戻って,この棒を積極的に
回転させようとする力![]() が存在する場合を考えよう。
が存在する場合を考えよう。![]() が
ある一定値をとる場合のつり合い式(6.1)の
結果を図-6.5の
が
ある一定値をとる場合のつり合い式(6.1)の
結果を図-6.5の![]() の領域に破線で示した。
図からも明らかなように明確な分岐点が無い。それは,この
外力
の領域に破線で示した。
図からも明らかなように明確な分岐点が無い。それは,この
外力![]() によって
によって![]() という解がつり合い式の解ではなくなるから
であり,外力レベルの低い段階からすでに回転し始めているからである。
明確な分岐点は存在しないが,
という解がつり合い式の解ではなくなるから
であり,外力レベルの低い段階からすでに回転し始めているからである。
明確な分岐点は存在しないが,![]() が
が![]() に近づくほど
回転角の増加傾向が大きくなり,非線形挙動を示しながら回転角が増大する。
さらに外力レベルが大きくなるにつれて,
に近づくほど
回転角の増加傾向が大きくなり,非線形挙動を示しながら回転角が増大する。
さらに外力レベルが大きくなるにつれて,![]() の分岐後の解に
漸近していくような挙動を示している。
の分岐後の解に
漸近していくような挙動を示している。
エネルギ的な考察を前節と同様に行うと,式(6.1)が
仮想仕事の原理になるような![]() の第1変分を
の第1変分を
と置くことにより,この第2変分を求めると
が安定規準であり,式(6.6)に一致する。
この安定規準は図示されていないが,図中の破線のつり合い状態は
安定な経路である。
このような一定外力![]() の存在は,棒を最初から少しだけ回転させる
影響を持っており,後述の初期不整の存在とほぼ同じ
影響を与えている。
実際に我々の身の回りで起こっていることは,このような
初期不整の存在のもとでの非線形挙動であり,
の存在は,棒を最初から少しだけ回転させる
影響を持っており,後述の初期不整の存在とほぼ同じ
影響を与えている。
実際に我々の身の回りで起こっていることは,このような
初期不整の存在のもとでの非線形挙動であり,![]() のときに
得たような,明確な分岐点が存在して変形挙動が急変するということは
滅多に起きないと考えるべきである。
のときに
得たような,明確な分岐点が存在して変形挙動が急変するということは
滅多に起きないと考えるべきである。
実際,ものさしの例に戻ってみると,たいていのものさしは
完全にまっすぐとは言えず,最初から少しだけ曲がっているだろう。
したがって,30cmものさしを手で押したときの挙動は
明確な分岐点の無い図-6.5の破線のようなものと
予想され,加える力がある
レベルに近づくにつれて曲がり具合の程度が「急に」増大する可能性がある。
そのため,ものさしを押したときに「突然」曲げが大きくなるように
感じたのである。![]() の
ときに観察できるような明確な分岐は,いわゆる完全系
,つまり最初の状態が理想的にまっすぐな系のみに起こることを
留意しておいて欲しい。
の
ときに観察できるような明確な分岐は,いわゆる完全系
,つまり最初の状態が理想的にまっすぐな系のみに起こることを
留意しておいて欲しい。
さらに少し別な見地から安定を捉えてみよう。図-6.6に
示したように,あるつり合い状態では
外力![]() の作用によりこの載荷点は左方に
の作用によりこの載荷点は左方に![]() だけ変位している。
このつり合い状態から
だけ変位している。
このつり合い状態から![]() をさらに増加させるために
もし
をさらに増加させるために
もし![]() も増加させなければならないようなら,その系は安定であろう。
すなわち
も増加させなければならないようなら,その系は安定であろう。
すなわち
![]() であれば
そのつり合い状態は安定と考えられる。
式(6.7)と
であれば
そのつり合い状態は安定と考えられる。
式(6.7)と
![]() とを考慮すると
とを考慮すると
となり,式(6.8)の条件と一致する。
このように,外力増分とその方向の載荷点での変位増分とを結び付ける剛性を
つり合い状態で算定し,その符号を用いることによっても
安定・不安定を議論できそうだ。
特にポテンシャルエネルギの存在しない現象やモデル等では,
このようにして安定を判定できるかもしれない。
この
![]() をつり合い点
での接線剛性
と呼ぶことがある。
接線剛性が零になる瞬間が分岐点に相当し,
接線剛性が正になる条件が安定規準になる。
をつり合い点
での接線剛性
と呼ぶことがある。
接線剛性が零になる瞬間が分岐点に相当し,
接線剛性が正になる条件が安定規準になる。
以上で説明したのと
同様の分岐現象を示す薄板は,実は分岐後の変位がそれほど
大きくならず,比較的大きな抵抗力を保持できることがわかっている。
さらに,一度分岐したあとに,
別の異なる特性の分岐点が現われる等の複雑な挙動を示すことがある。
これに対して梁や柱の場合には,最初の分岐後の変位が比較的大きくなってしまい,
一旦分岐してしまうと,分岐後が安定なつり合い状態であっても
変形が大きくなり過ぎ,
実際の多くの材料は降伏して抵抗力を保持できなくなる。
このことはつまり,梁や柱の場合には,最初の分岐点近傍の挙動だけを
知ることができれば工学的には十分な場合が多いということを示唆している。
そこでここでは,![]() のつり合い状態の
近傍だけを取り扱うことができるような,比較的小さい変位状態に
おけるつり合いの範囲内で安定を論じてみよう。
元の有限変位理論をあるつり合い状態近傍で線形化した理論である
ことから,線形化された有限変位理論
と呼ばれることもある。
のつり合い状態の
近傍だけを取り扱うことができるような,比較的小さい変位状態に
おけるつり合いの範囲内で安定を論じてみよう。
元の有限変位理論をあるつり合い状態近傍で線形化した理論である
ことから,線形化された有限変位理論
と呼ばれることもある。
式(6.1)で![]() という近似を
用い,
という近似を
用い,
![]() ,
,
![]() を
代入するとつり合い式は
を
代入するとつり合い式は
となる。したがって
という関係を得る。ここでは式(6.4)の![]() を
用いている。
を
用いている。![]() のときの分岐点は,
式(6.14)が
のときの分岐点は,
式(6.14)が![]() で
で![]() の解を
持つ条件から
の解を
持つ条件から![]() と求められる。
零でない
と求められる。
零でない![]() を一定に保つような与え方をしたときの外力と回転角との
関係を図-6.7に実線で示した。
図中の破線は式(6.1)を用いた厳密解である。
式(6.15)の表現からも明らかなように,
を一定に保つような与え方をしたときの外力と回転角との
関係を図-6.7に実線で示した。
図中の破線は式(6.1)を用いた厳密解である。
式(6.15)の表現からも明らかなように,![]() からの
連続したつり合い経路は
からの
連続したつり合い経路は![]() 以上には決して及ばない。
しかし,小さい変位の領域では厳密解との差異が非常に小さいことは,
この図における比較から明らかである。
特に分岐点近傍での挙動さえわかればいいのであれば,
この程度の近似理論で十分であることもわかる。もし
以上には決して及ばない。
しかし,小さい変位の領域では厳密解との差異が非常に小さいことは,
この図における比較から明らかである。
特に分岐点近傍での挙動さえわかればいいのであれば,
この程度の近似理論で十分であることもわかる。もし
と定義すると,式(6.15)は
とも書け,![]() は外力
は外力![]() の影響を増幅する係数としても
捉えることができる。
の影響を増幅する係数としても
捉えることができる。
安定規準についてもエネルギ的アプローチに従えば,つり合い式から
と第1変分を表すことができるので,安定規準は第2変分を用いて
すなわち![]() であることがわかる。
文献[73]等では,線形化された理論の範囲内
での内部ひずみエネルギと外力ポテンシャルとの等置で
安定規準を決定しているが,
であることがわかる。
文献[73]等では,線形化された理論の範囲内
での内部ひずみエネルギと外力ポテンシャルとの等置で
安定規準を決定しているが,![]() の存在がある場合に
そのアプローチには疑問が生じる等,正確な安定規準ではない。
エネルギ的に安定を論ずる場合には必ず第2変分で議論すべきである。
の存在がある場合に
そのアプローチには疑問が生じる等,正確な安定規準ではない。
エネルギ的に安定を論ずる場合には必ず第2変分で議論すべきである。
初期不整
がある場合も同様に議論できる。図-6.8の
ように角度を定義し,![]() が外力を作用させる前に
存在していた初期不整であるとしよう。モーメントのつり合いが
が外力を作用させる前に
存在していた初期不整であるとしよう。モーメントのつり合いが
となり,![]() および
および
![]() の近似をすると
の近似をすると
となる。ここに![]() は式(6.16)で定義した係数で,
やはり初期不整の影響の増幅率としても
捉えられる。
は式(6.16)で定義した係数で,
やはり初期不整の影響の増幅率としても
捉えられる。![]() を与えた場合の
を与えた場合の![]() と
と![]() の
関係を図-6.9に示した。
図中の破線は式(6.17)の厳密な挙動で
ある。図-6.9と図-6.7とを
比較しても明らかなように,完全系を壊そうとするような外力の
影響と初期不整の影響とは本質的に同じ効果を持ち,
式(6.16)で定義した
の
関係を図-6.9に示した。
図中の破線は式(6.17)の厳密な挙動で
ある。図-6.9と図-6.7とを
比較しても明らかなように,完全系を壊そうとするような外力の
影響と初期不整の影響とは本質的に同じ効果を持ち,
式(6.16)で定義した![]() で応答が増幅されている。
で応答が増幅されている。
比較的変位が小さい理論の範囲でエネルギ的アプローチによる
安定規準
をまとめると
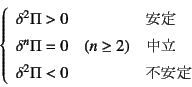 |
(6.18) |
となる。通常![]() になる分岐点を「中立」
と分類することが多いが,
それはこの比較的変位の小さい理論の範囲内での
分類であることに注意する。図-6.5にも
示したように,有限変位理論の範囲内であれば分岐点での
ポテンシャルエネルギはまだ下に凸の汎関数になっており,
このモデルの場合は
になる分岐点を「中立」
と分類することが多いが,
それはこの比較的変位の小さい理論の範囲内での
分類であることに注意する。図-6.5にも
示したように,有限変位理論の範囲内であれば分岐点での
ポテンシャルエネルギはまだ下に凸の汎関数になっており,
このモデルの場合は
| (6.19) |
と第4変分以降が正の値をとるため,分岐点そのものは安定である。 したがって安定条件も厳密には最低次の非零変分量が正であることと 書き改める必要はあるだろう。 式(6.14)をもっと高次項まで考えながらエネルギ的考察で 初期不整感度等を組織的にまとめた文献としては, 文献[14]等が挙げられる。
ところで,
分岐後の状態が必ずしも安定であるとは限らないことを示すために,
回転バネではなく,通常の伸び縮みバネで同じように支えられた
剛棒のモデル(図-6.10)の挙動を考えてみよう。
この系の場合の分岐荷重は
![]() となるのであるが,
分岐後の挙動も図-6.3のモデルとは全く異なっている。
厳密解は文献[126]等に詳しいし容易に導くことが
できるので割愛するが,その挙動を図-6.11に
まとめた。
となるのであるが,
分岐後の挙動も図-6.3のモデルとは全く異なっている。
厳密解は文献[126]等に詳しいし容易に導くことが
できるので割愛するが,その挙動を図-6.11に
まとめた。
図中の一点鎖線が![]() のときの安定条件で,
この線より上方が不安定,下方が
安定な領域である。したがって,
のときの安定条件で,
この線より上方が不安定,下方が
安定な領域である。したがって,![]() なら分岐点までの
なら分岐点までの![]() の
状態のみが安定である。
また,回転させようとする外力
の
状態のみが安定である。
また,回転させようとする外力![]() が存在する場合にはそのピークまでの
つり合い状態のみが安定である。
自然界では不安定な状態を維持できないため,
この系では一点鎖線よりも下方のつり合い状態以外を観測することはできない。
しかも前の回転バネの場合とは異なり,
分岐点における全ポテンシャルエネルギの分布は同図の右側に
示したように上に凸であり,不安定な分岐点である。
すなわち,この場合は
が存在する場合にはそのピークまでの
つり合い状態のみが安定である。
自然界では不安定な状態を維持できないため,
この系では一点鎖線よりも下方のつり合い状態以外を観測することはできない。
しかも前の回転バネの場合とは異なり,
分岐点における全ポテンシャルエネルギの分布は同図の右側に
示したように上に凸であり,不安定な分岐点である。
すなわち,この場合は
| (6.20) |
となっているため,分岐点は不安定になる。 こういった詳細は比較的小さい変位の枠の中での 安定条件では判別できないので注意する必要がある。 弾性構造の座屈および座屈後の挙動についての詳細な説明は, 例えば文献[14]等に詳しいので参照のこと。