最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。

• 6.3.1 2種類の座屈現象
  • 6.3.1.1 分岐座屈
  • 6.3.1.2 極値座屈
  
  
• 6.3.2 座屈点およびそのあとの挙動
  • 6.3.2.1 飛び移り現象
  • 6.3.2.2 屈服現象
  • 6.3.2.3 座屈は幾何学的な変化が原因，しかし・・・

6.3 座屈現象の特徴と例

6.3.1 2種類の座屈現象

6.3.1.1 分岐座屈

図 6.12: 柱の曲げ座屈

今まで見てきた不安定現象は分岐現象 と呼ばれているが， その他の不安定現象も含めて，構造力学では座屈現象 と総称している。 座屈現象そのものは次に示すように，通常二つに分類される。 また座屈後の挙動もその次に示すように，2種類に分類され 区別されることがある。

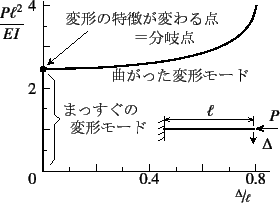
剛体バネモデルで見たように，ある変形状態において， そこに至るまでの変形の特徴とは大きく異なる特性を有する変形状態に突然 移行する現象がある。図-6.12には最も代表的な分岐座屈 の例，すなわち次節以降で取り扱う柱の曲げ座屈挙動を示したが， 前節の回転バネでできたモデルの挙動に非常によく似ている。 つまり，図中に示したような片端固定の柱を圧縮していくと， ある外力レベルに達するまではたわみが発生せず， 柱はまっすぐのまま縮む変形のみが生じる。 ところがその外力レベルに至ったところで，それまでと同じく単純に 縮むつり合い形状と，曲がってつり合う形状との2種類のつり合い状態が 可能になる。 さらに大きい外力レベルに対しては，まっすぐ縮むつり合い 状態が不安定になり，曲がった状態の方が安定になる。したがって自然界では 曲がった状態が選択され，柱は曲がる。 このように，変形の特徴の大きく異なる二つ以上のつり合い状態が 可能になる臨界点を分岐点 と称し，分岐点に至るまでの変形の特徴と異なる特性を持った つり合い状態に突然移行する現象を分岐座屈 と呼んでいる。

図 6.13: 分岐現象の例

もう一つの代表例を図-6.13に示したが， 浅い角度で交わる骨組や盛り上がりの浅いアーチ等で 顕著な現象である。 この系は外力も構造も左右対称であるから，外力の 増加に伴って生じる変形も左右対称だと考えられる。 確かに点Bに到達するまでは左右対称な変形を示している。 しかしこの点Bにおいて左右非対称な変形モード， 例えば右半分には上に凸の曲げ変形が生じ，左半分には下に凸の 曲げ変形が生じてつり合うという変形モードが可能になるのである。 つまり点Bが分岐点で，経路B$\to$Cは左右非対称な変形モードである。 しかもこの場合の分岐経路B$\to$Cは，前の例とは異なり， 不安定なつり合い状態になっている。一方，点Bを過ぎて点Aのピークを 通過して点Cに至るつり合い経路は左右対称な変形を保持した つり合い状態になっている。 しかしこれも不安定なつり合い状態である。 そんな点Bでどんなことが起こり得るのかについては次の節で説明する。

6.3.1.2 極値座屈

図-6.13と同じような構造ではあるが， 尖り具合の異なる骨組やアーチでは点Bのような（対称変形が 非対称変形に移行するような）分岐点が存在しない場合がある。 その場合には点Aまでの左右対称のつり合い状態は安定である。 しかし，点Aに到達したあとのCに向けて下降するつり合い経路は 不安定であり，実験でこの経路のつり合い状態を観察するには工夫が必要になる。 つまり点Aもある種の不安定点である。 このように，つり合い経路に極値が存在した 場合にも系は不安定になる。このような座屈は分岐座屈とは 呼べず，通常は次節で分類する座屈後の挙動で分類することが多い。 ただ，かつてはこれを屈服座屈[91]と呼んでいたようだが， この文書では分岐座屈との差異を表現するために極値座屈 という造語を新たに導入しておく。 同じような座屈は後述の薄肉円管の曲げ（6.16）でも 起こる。 ただし不安定になる規準は， 分岐座屈の規準のうちの節-6.2.3で示した 接線剛性を用いた規準と同じになる。

6.3.2 座屈点およびそのあとの挙動

6.3.2.1 飛び移り現象

前節の分岐点および極値になる点を，いずれも座屈が発生する状態で あることから座屈点 と称しておく。図-6.12の柱の場合には， 座屈したあとも材料が降伏等せずに抵抗を失わなければ， 連続して安定なつり合い経路が存在する。したがって， 柱は単に曲がっていくだけで外力には静的に抵抗し続けられる。 しかし，図-6.13のアーチ状の骨組の例では，点Bであれ 点Aであれその座屈点以降にそういった 安定なつり合い経路が連続しては1本も存在しない。 これは，図-6.10の伸び縮みバネ剛棒モデルと 同じ特徴である。 このように座屈点を過ぎた経路に安定なつり合い状態が連続して いない場合には，実験等では動的な応答が 見られる。図-6.13の場合も点Bの分岐点直後の 連続したつり合い状態が二つ共不安定であるため， 荷重を単調に増やしていく実験の場合には， 点Bの状態から右方の $\slfrac{\Delta}{\ell}$が0.15あたりの 安定な状態にまで動的に移行する現象が観察される。 このように，あるつり合い点から，それと連続しない 他の安定なつり合い点へと動的に移行する現象を飛び移り現象 と称している。

もし，この図-6.13の点AあるいはBのレベルがさほど高くなく， 同時に点Cが縦軸外力$P$の少しだけ正のレベルにあるような応答をする 構造系（必ずしもこのようなアーチ形式とは限らない）を 作ることができれば，パーソナルコンピュータの キーボードの各キーの支持構造を作ることができる。 つまり，小さい力（低レベルのAあるいはB）でキーを押し込むことができ， キーはそのまま飛び移って深く沈む。その指を添えている間（点Cの レベルより少しでも高い外力レベルで）は， キーは深く沈んだ状態に維持される。 最終的に指を浮かすと（点Cが$P$のわずか正レベルにあれば）， 点Cよりも外力レベルが下がるときに点Cで再度飛び移りが生じ， 自動的にキーは元の位置に戻ることになる。 このようなキーボードは使っていて疲れないことが容易に予想できるだろう。 座屈を有効利用した例である。

図 6.14: Williamのトグル

それに似た， もう一つの代表例を図-6.14に示した。 これはWilliamのトグル と呼ばれる構造系で，前節の例と同じような骨組だが 両端が固定されている。この場合には分岐点は無いが， 外力を増加させてあるレベルに達するとピークに到達する。 このピーク点は前節の極値座屈点であり， そのあとに連続するつり合い状態は不安定である。 しかし，同じ外力レベルでそれよりも大きい変位$\Delta$の 状態に別の安定つり合い点が存在する ため， $\slfrac{\Delta}{\ell}$が0.04あたりの安定 状態へと動的に飛び移ることになる。 飛び移ったあとは安定であるが，その状態から逆に 外力$P$を減少させていくと，今度は下に凸の ピークに当たるつり合い状態から $\slfrac{\Delta}{\ell}$が0.01あたり の安定状態へと飛び移ることになる。 実はこういった現象を示す座屈を「飛び移り座屈」と呼ぶ[91]ことが ある。しかし，分岐座屈する図-6.13の場合も分岐点で 飛び移り現象が発生するため，座屈の分類として「飛び移り座屈」という 言葉を使うのは適切ではないと考える。

図 6.15: 飛び移り現象と髪留め・ビードロ

さて，このような現象を見ると，座屈現象が必ずしも普通の生活とは無縁な力学 現象ではないことに気付く人もいると思う。上記のキーボードの キー支持構造以外でも，例えば，ある種の廉価な 「髪留め」 やプラスティックの携帯用「ヘアブラシ」等にも， この飛び移り現象を利用したものがある。またガラス玩具 「ビードロ」 もWilliamのトグルと同じ原理で 音を出していることは，容易に想像できると思う。 また橋構造では終局状態の一つである（悪者の）座屈も， それが必要不可欠な機能である構造もあり得る。 例えば太陽電池のような巨大な宇宙構造物 を分解した部品にしてスペースシャトルで運ぶと， 宇宙空間で組み立てる必要が生じ，その作業には手間と大きな危険が伴うだろう。 しかし全体構造をそのまま地上で，例えば座屈を有効利用して 比較的小さい外力でたたむこと（力を加えた ときの飛び移りを利用）ができ， 同時に宇宙では，シャトルから放出すると自分自身で展開（力を除くときの 飛び移りを利用）できれば非常に便利である。 このような構造を自己展開型構造 と呼んでいる。その一例としては， 自動車の窓の内側に吸盤で貼り付ける網状の シェードがある。 通常はねじることによって10cm程度の 直径の3重の輪状になって収納されているが，利用するときには 取り出して手を離すだけで，自身の力で窓の大きさに拡がる。

6.3.2.2 屈服現象

図 6.16: 半径$r_0$肉厚$t$の薄肉円管の曲げ

ピークや分岐点における外力レベルでの状態が安定であっても， 外力を除去して元に戻る場合以外には安定なつり合い状態が 全く存在しない場合には， 飛び移る先すら無いことから，系はそのまま崩壊してしまう。このような 不安定現象は屈服現象 と呼ばれる。図-6.16に 示したのは，薄肉円管に等曲げを作用させたとき の挙動[45]である。節-E.5には 一つの近似的な解析法を示したが， 肉厚が非常に薄い管なので，最初は円形をしていた断面が， 曲げが加わるにつれて上下につぶれ始めて楕円形状になるのである。 それに伴い梁の 高さが小さくなるため，断面2次モーメントも小さくなり， 次第に実質的な曲げ剛性が小さくなる。その影響で，図に示したように 断面変形の無い線形挙動から下方にずれ始める。 最終的には，断面がある程度偏平な楕円形状に なったところで抵抗力のピークを迎えて崩壊に至る。 これも「屈服座屈」と称する[91]ことがあるが， 不安定分岐座屈のように座屈後に安定なつり合い状態の存在しない分岐座屈も あり得るため， この文書ではそういった分類を避けた。

6.3.2.3 座屈は幾何学的な変化が原因，しかし・・・

このような座屈は構造工学的に非常に重要な問題で， 特に圧縮を受ける鋼構造部材の設計に当たっては必ず考慮しなければ ならない。 特に，材料としての強度にはまだ余裕があるにもかかわらず， ちょっとした変形による幾何学的な原因で構造系が強度を失う現象を 座屈と捉えていることに留意すべきである。 例えば図-6.16のような現象は降伏等の 材料的な限界によっても発生し得るが， 単に材料非線形性のみによって生じる同様の応答は座屈とは呼ばないのが普通である。 つまり座屈は，幾何学的な非線形性 が原因となって起こる変形特性の急激な変化を指すのである。 ただ，「分岐」や「屈服現象」が材料非線形性 によって起こることも事実であり， 最近ではそういった不安定現象を総じて座屈と呼ぶ場合もある。 例えば鋼の引張り試験では，破断に近づくにつれて試験片の断面が 小さくなる「絞り」が生じる。 このやや微視的な原因は，多数の離散的なすべり線が引張り軸方向とある角度を 持った方向に生じたこととされている。 これは材料非線形性に起因した不安定現象の代表例である。 そのようなものも含め，塑性座屈等についても 文献[36]等を参照して欲しい。

最新版を正確に読むためには pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。