| (E.52) |
最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
章-6で扱った梁-柱理論は,
ひずみと変位との関係式の非線形項の一部を近似することによって
求められる。まず伸びについては,式(E.11b)で
軸方向変位勾配の非線形項を無視し,式(E.17b)を
と近似する。これは式(6.29b)にも示した。
また曲率についても式(E.17c)における
非線形項を無視し
と近似する。
断面力と変形の関係は式(E.30)が,内力仮想仕事項も
式(E.24)がそのまま成立するものとする。
分布外力のうち軸方向成分![]() を無視すれば,その仮想仕事式
が
を無視すれば,その仮想仕事式
が
となる。
式(E.55)の変分を実行することによって支配方程式を得る。
つり合い式は
であり,式(6.24)に一致している。
また境界条件は
となり,これも式(6.25)が求められている。
章-6でも扱ったように,
境界条件が簡単な通常の柱の場合には,式(E.56a)の
つり合い式が式(E.57a)の境界条件のもとで簡単に解け
という関係式(6.26)が成立する。
したがって曲げに関する支配方程式の部分が,例えばつり合い式は
となる等,式(6.30)が 求められ,境界条件は式(6.31)に一致する。 このように梁-柱理論は,伸びひずみと 変位の関係におけるたわみ角の2次項を考慮することによって 得ることができた近似理論であることがわかる。
仮想仕事式が式(E.55)で与えられており,変形と 変位の関係が式(E.53) (E.54)で与えられ, 断面力と変形の関係は式(E.30)が成り立つから, 変位成分を適切な関数で仮定すれば,章-5で 紹介した有限要素法による近似つり合い式,つまり剛性方程式を 求めることができるはずだ。
そこで軸方向変位は1階の微係数しか現われていないことから,
式(5.15)の1次多項式で変位を仮定する。
たわみも微小変位理論の場合と同様の条件でいいから,
式(5.20)の3次多項式を用いることにする。
これを仮想仕事式等に代入して整理すると,
この場合は変位の非線形項が含まれていることから,
剛性方程式も非線形になる。それは
の順番で左辺の配列の成分を定義し,![]() 等は
すべての添え字に対して対称な(入れ替えても同じ値を持つ)
配列として定義できる。その具体的な
値を表-E.1〜E.1に与えた。
線形部分の
等は
すべての添え字に対して対称な(入れ替えても同じ値を持つ)
配列として定義できる。その具体的な
値を表-E.1〜E.1に与えた。
線形部分の![]() は,式(5.37)で
定義した剛性行列と一致している。
は,式(5.37)で
定義した剛性行列と一致している。
式(E.58)の形は,計算機で解く場合には何の不都合も
無い形式をしているが,これを敢えて行列表示することもできる。
そこで,非線形項の最初の部分だけを行列表示してみよう。すなわち
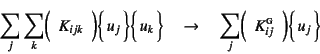
のように表示してみたい。この
![]() は
もちろん
は
もちろん![]() の関数行列となる。
まず対称行列になるように並べると
の関数行列となる。
まず対称行列になるように並べると
となる。ここに
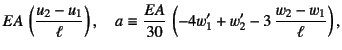 |
(E.60) | ||
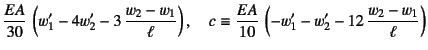 |
と置いたが,![]() は近似的にこの有限要素の軸力と考えていい。
あるいは,対称ではない形式で示すこともでき,その場合は
は近似的にこの有限要素の軸力と考えていい。
あるいは,対称ではない形式で示すこともでき,その場合は
と書くことができる。この行列の第1, 4行目を除いた部分は
式(E.60)のそれと同じであり,
式(6.59)で定義した幾何剛性行列
の![]() を
を![]() で置き換えたものと等価な対称行列になっている。
で置き換えたものと等価な対称行列になっている。
式(E.62)で式(6.59)の幾何剛性に含まれていない
部分には,![]() ,
, ![]() が全く含まれず,たわみ
が全く含まれず,たわみ![]() および
たわみ角
および
たわみ角![]() の2次項しか含まれていない。また式(E.58)の
右辺第3項もすべて同様の非線形項である。このことから,
幾何剛性行列の式(6.59)が座屈点近傍までの
範囲での「第1次近似」としては充分な精度を有していることが
推測される。ちなみに,式(6.59)の幾何剛性の通常の誘導は,
式(E.53)のひずみ変位関係を仮想仕事の式(E.55)に
代入して変分することによって得ることができる内力仮想仕事項を,まず
の2次項しか含まれていない。また式(E.58)の
右辺第3項もすべて同様の非線形項である。このことから,
幾何剛性行列の式(6.59)が座屈点近傍までの
範囲での「第1次近似」としては充分な精度を有していることが
推測される。ちなみに,式(6.59)の幾何剛性の通常の誘導は,
式(E.53)のひずみ変位関係を仮想仕事の式(E.55)に
代入して変分することによって得ることができる内力仮想仕事項を,まず
とする。その上で,被積分関数の第1項の![]() を
を![]() と近似した上で,
第2項の
と近似した上で,
第2項の![]() を外力圧縮力で
を外力圧縮力で![]() と置き換え,モーメントと曲率の関係を
代入して
と置き換え,モーメントと曲率の関係を
代入して
| (E.62) |
と表される仮想仕事式に適切な変位関数を代入することによって, 式(6.59)の幾何剛性を得ることができる。
ここではTimoshenko梁のいわゆる幾何剛性を求めるために,
線形化した仮想仕事式から定式化を始める。
詳細は文献[29]を参照のこと。
外力仮想仕事はBernoulli-Euler梁と同じなので割愛し,
内力仮想仕事項と軸圧縮力![]() の仮想仕事項だけを示すと
の仮想仕事項だけを示すと
となる。付録-Dでも述べたように,精度のいいものを
得るには,たわみ![]() には3次の多項式を仮定し,せん断変形
には3次の多項式を仮定し,せん断変形![]() に
一定を仮定した上で,最終的には
に
一定を仮定した上で,最終的には![]() を消去する必要がある。
外力ベクトルと変位ベクトルを
を消去する必要がある。
外力ベクトルと変位ベクトルを
| (E.64) |
と定義すると,要素剛性方程式は
| (E.65) |
となる。ここに![]() は有限要素の長さである。
行列
は有限要素の長さである。
行列
![]() が幾何剛性行列
である。具体的には
が幾何剛性行列
である。具体的には
になる。ここに
![]() は式(4.85a)で
定義したパラメータである。また
は式(4.85a)で
定義したパラメータである。また
| (E.67) |
と定義した。