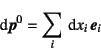 |
(E.1) |
最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
この章タイトルにある有限変位というのは,微小ではない変位の
ことを指す。章-3では微小変位の場合のひずみや
応力を定義したが,ここでは有限変位の範囲のひずみの定義をする。
詳細は章-12を参照のこと。さて
変位前の物体中の任意点の位置ベクトルは
式(3.1)で表すことができるから,任意の微分要素ベクトルは
と表現できる。ただし,ここでは直角座標での説明をするため,
テンソルの共変成分
・反変成分
の区別をせず,すべて下付きの指標で成分を表すことにする。
極座標等の一般的な厳密な表現については
例えば文献[24]を参照のこと。
一方,式(3.3)を考慮すると,
変位後の位置ベクトルの式(3.2)から同様に
と書くことができる。ここに![]() は
は
で定義した変形後の基底ベクトルである。
これは,変形前に空間座標系基底ベクトル![]() と一致するように
定義した上で物体各点に糊付けしたもので,
物体と一緒に変位して変形するベクトルである。
したがって元の基底ベクトル
と一致するように
定義した上で物体各点に糊付けしたもので,
物体と一緒に変位して変形するベクトルである。
したがって元の基底ベクトル![]() が単位の直交ベクトルで
定義されたとしても,
が単位の直交ベクトルで
定義されたとしても,![]() の方は単位でもなく互いに直交も
しないベクトルの組になっている。
の方は単位でもなく互いに直交も
しないベクトルの組になっている。
ひずみは変形前後の微分要素の長さの差として式(3.10)で
定義されたから,上式をこれに代入して整理すると
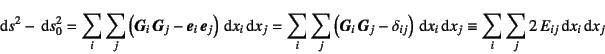
のようにしてひずみ成分![]() を定義できそうだ。
式(3.10)と同じ表現であるが,式(3.10)の
場合はその線形部分だけが成立していた。
つまり,有限変位におけるひずみテンソル成分としては厳密に
を定義できそうだ。
式(3.10)と同じ表現であるが,式(3.10)の
場合はその線形部分だけが成立していた。
つまり,有限変位におけるひずみテンソル成分としては厳密に
で定義する。このひずみテンソル![]() をGreenのひずみ
テンソルと呼ぶ。
式(E.2)の
をGreenのひずみ
テンソルと呼ぶ。
式(E.2)の![]() の定義を式(E.4)右辺に
代入して整理すると,各成分は
の定義を式(E.4)右辺に
代入して整理すると,各成分は
と定義できる。右辺括弧内第3項が式(3.6)で定義された 微小変位におけるひずみ成分には無かった非線形項である。
物理的な意味について,代表的な成分と微小変位の場合の成分とを
比較してみよう。まず![]() は
は
となるから,ひずみ自体が微小である限り,式(3.4)の
伸びひずみと近似的に一致する。
一方![]() は
は
となる。これもひずみ自体が微小である限り,式(3.5)の せん断ひずみと近似的に一致する。
前節で定義したGreenのひずみテンソル成分を用いた仮想仕事式は,
その誘導は省略するが,式(B.1)と形式的には同じく
と
表現される。
ただし![]() は第2 Piola-Kirchhoff応力
テンソル成分である。
物理的には,変位前に単位面積を持ち変位後に
は第2 Piola-Kirchhoff応力
テンソル成分である。
物理的には,変位前に単位面積を持ち変位後に![]() 方向を
法線ベクトルとする面積要素当たりの,
その物体点の変位後の基底ベクトル
方向を
法線ベクトルとする面積要素当たりの,
その物体点の変位後の基底ベクトル![]() 方向の力成分を表している。
したがって,変形後の基底ベクトルが必ずしも単位ではないことから,
それ自体は物理的な応力の大きさと次元とを持っておらず
方向の力成分を表している。
したがって,変形後の基底ベクトルが必ずしも単位ではないことから,
それ自体は物理的な応力の大きさと次元とを持っておらず
という調整が必要であることに注意する。
以下簡単のために,添え字の![]() の組を
の組を![]() で記す。
で記す。
最初は少し一般性を持たせるために,まず,せん断変形の影響を
含んだTimoshenko梁モデル[37,41]に対して
運動場を誘導する。付録-Dで提示した運動場
に対する仮定を図-E.1に示した。
式(4.3)のようにはsineとcosineを
近似せず,式(D.2)をきちんと書くと
となる。![]() は断面の回転角である。
軸線は断面の図心を通るものとするが,変形前に軸線と
平行していた棒の線素は,変形後には
は断面の回転角である。
軸線は断面の図心を通るものとするが,変形前に軸線と
平行していた棒の線素は,変形後には![]() 方向を向く。したがって
線素の向きは
方向を向く。したがって
線素の向きは![]() 軸
と
軸
と
![]() の
角度をなす。
の
角度をなす。![]() は断面のせん断変形による角度変化である。
このことから,軸線の変位と傾きの幾何学的関係は
は断面のせん断変形による角度変化である。
このことから,軸線の変位と傾きの幾何学的関係は
となる。ここにプライムは![]() に関する微分を表し,
下添え字に0が付いた
に関する微分を表し,
下添え字に0が付いた![]() ,
, ![]() はそれぞれ,
基底ベクトルの回転角
はそれぞれ,
基底ベクトルの回転角![]() および
および![]() の
軸線上(
の
軸線上(![]() )での値を表す。
)での値を表す。
式(E.9)を考慮しながら式(E.8)を ひずみの定義式(E.5)に代入して整理すると
(E.10)
と表すことができる。ここに
![]() で
で
と定義した。
式(E.9)と式(E.11)の定義を用いると,
変位勾配は
という関係にあることを示すことができる。
変形前に軸線と平行だった任意の線素の向きは,
断面任意点での変形後の基底ベクトルの回転角と変形の関係式
で与えられる。あるいは,せん断変形部分だけについては
という関係がある。