最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。

• B.1.1 3次元問題の仮想仕事式
• B.1.2 平面ひずみ問題の応力ひずみ関係

B.1 仮想仕事式と応力ひずみ関係

B.1.1 3次元問題の仮想仕事式

章-3の連続体力学に章-5の有限要素法を 適用し，連続体の問題を近似的に解くための基礎式を誘導しよう。 ただし例としては，式(3.109)で与えられる平面ひずみ問題を 対象とし，文献[18]の表現を用いた基礎式の 列挙をするだけである。

一般的な表現は式(3.95)に示したが，仮想的な変位を 用いてそれを書き直そう。図-3.9にあるように， 領域$V$を占め適切に支持された物体に体積力$\fat{X}$が作用し， 表面$S$の一部に表面力$\fat{F}$が作用あるいは発生してつり合っている。 この物体の各点を仮想的に$\delta\fat{u}$だけ変位させた^B.1と考えて， つり合い式(3.22)に対応する弱形式を求めると

$$0= -\int_V \sum_{i=1}^3 \left[ \sum_{j=1}^3 \D{\sigma_{ji}}{x_j} + X_i\right] \delta u_i \dint V$$

となる。被積分関数第1項にGaussの発散定理を適用し， 式(3.24b)の力の境界条件を代入すれば

$$=\int_V \sum_{i=1}^3 \sum_{j=1}^3 \sigma_{ji} \delta \D{... ...\dint V - \int_{S} \sum_{i=1}^3 F_i \delta \bar{u}_i \dint S$$

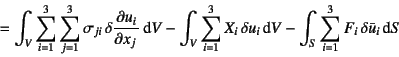
と書き表すことができる。ただしこの$\fat{F}$は上述のように， 境界で与えた外力だけではなく， 変位を与えた表面部分ではそこでの反力をも表していることにする。 また表面では $\delta\bar{\fat{u}}$と上棒付きで書いたが， これも必ずしも表面で与えられた変位というわけではなく， 境界での値であることを明示するために便宜上用いたものである。 この第1項は

$$\sum_{i=1}^3 \sum_{j=1}^3 \sigma_{ji} \delta \D{u_i}{x_j}= ... ...,\delta \D{u_i}{x_j}+ \sigma_{ij} \delta \D{u_j}{x_i}\right)$$

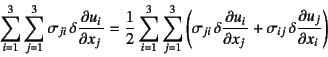
と書いてもよく，これにモーメントのつり合い式(3.23)を 用いると

$$=\sum_{i=1}^3 \sum_{j=1}^3 \sigma_{ji} \dfrac{1}{2} \delta \left(\D{u_i}{x_j}+\D{u_j}{x_i}\right)$$

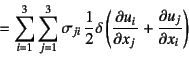
とも表すことができる。したがってひずみの定義式(3.6)を代入すれば

$$=\sum_{i=1}^3 \sum_{j=1}^3 \sigma_{ji} \delta \epsilon_{ji}$$

と書くことができる。したがって仮想仕事式 は

$$\int_V \sum_{i=1}^3 \sum_{j=1}^3 \sigma_{ji} \delta \epsi... ... V -\int_{S} \sum_{i=1}^3 F_i \delta \bar{u}_i \dint S = 0$$ (B.1)

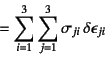
となる。

B.1.2 平面ひずみ問題の応力ひずみ関係

式(3.123)のように，平面ひずみ問題と平面応力問題は 同じ形式の応力ひずみ関係式で表現できるが， ここでは一例として平面ひずみ問題の方を対象とする。 したがって，応力ひずみ関係は式(3.109)で表される。 この逆関係は

$$\sigma_{xx}=(\lambda+2 \mu) \epsilon_{xx}+ \lambda \epsi... ... \mu) \epsilon_{yy}, \quad \sigma_{xy}=2 \mu \epsilon_{xy}$$

と表現できるが，式(3.43) (3.44)を 考慮して，Laméの定数の代わりにYoung率とPoisson比を用いると

$$\sigma_{xx} = \dfrac{E}{(1+\nu)(1-2 \nu)} \left\{(1-\nu) \epsilon_{xx}+\nu \epsilon_{yy}\right\},$$ (B.2)

$$\sigma_{yy} = \dfrac{E}{(1+\nu)(1-2 \nu)} \left\{\nu \epsilon_{xx}+(1-\nu) \epsilon_{yy}\right\}, \qquad \sigma_{xy}=\dfrac{E}{2(1+\nu)} 2 \epsilon_{xy}$$

とも表される。

最新版を正確に読むためには pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。