最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。

• B.2.1 変位関数
• B.2.2 剛性方程式
• B.2.3 等価節点外力
• B.2.4 数値解析例と応力の精度

B.2 定ひずみ三角形要素

B.2.1 変位関数

平面問題は$x$-$y$面内の問題だけで閉じていて，$z$方向の 成分はその結果を用いて算定できるから，応力ひずみ関係を 除けば，見かけ上2次元問題とは区別がつかない。 だから，平面ひずみ問題の仮想仕事式 も式(B.1)において

$$\int_V \sum_{i=1}^2 \sum_{j=1}^2 \sigma_{ji} \delta \epsi... ... V -\int_{S} \sum_{i=1}^2 F_i \delta \bar{u}_i \dint S = 0$$ (B.3)

のように，総和の範囲を2までに修正するだけでいい。 この仮想仕事式にひずみの定義式(3.6)と 構成方程式(B.2)を代入すれば，すべての項を 変位成分で表すことができる。 したがって，この変位成分を適切な変位関数で近似してやれば， 平面ひずみ問題に対する剛性方程式を求められるはずだ。

そこで，いくつかの行列を

$$\vect{\sigma} \equiv \lfloor\sigma_{xx}\quad\sigma_{yy}\quad\sigma_{xy}\rfloor\supersc... ...\lfloor\epsilon_{xx}\quad\epsilon_{yy}\quad 2 \epsilon_{xy}\rfloor\supersc{t},$$

$$\vect{u} \equiv \lfloor u_x\quad u_y\rfloor\supersc{t}, \quad \vect{X} \equiv \lf... ...rfloor\supersc{t}, \quad \vect{F} \equiv \lfloor F_x\quad F_y\rfloor\supersc{t}$$ (B.4)

と定義しておき，式(B.1)に代入すると

$$\int_V \delta\vect{\epsilon}\supersc{t} \vect{\sigma} \din... ...int V- \int_S \delta\vect{u}\supersc{t} \vect{F} \dint S = 0$$ (B.5)

と仮想仕事式を書くことができる。

この式(B.5)を見る限り，第1項の一番大切な 内力仮想仕事項には変位の1階の微係数しか現れない。 したがって，最も低次な要素は$x$, $y$の1次多項式以下で良いことになる。 つまり

$$\vect{u} =\left(\begin{array}{cccccc} 1&x&y&0&0&0\ 0&0&0&1&... ... \alpha_4\quad \alpha_5\quad \alpha_6 \right\rfloor\supersc{t}$$

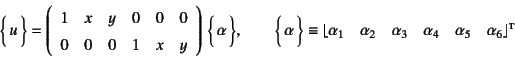
と置けばいい。この変位関数の未定係数$\alpha_i$は6個だから， 例えば図-B.1に示したような三角形要素を 考え，各頂点を要素の節点とし，その節点での$x$, $y$方向の 変位成分を有限要素の自由度とすれば，全部で6個の未定係数を この六つの変位成分で置き換えることができる。 このようにすると上式から

$$\vect{u}=\mat{N} \vect{q}$$ (B.6)

と置ける。ここに$\vect{q}$は節点変位成分であり

$$\vect{q} \equiv \lfloor u_1 v_1 u_2 v_2 u_3 ... ...ccc} N_1&0&N_2&0&N_3&0\\ 0&N_1&0&N_2&0&N_3 \end{array}\right)$$ (B.7)

と定義し，さらに

$$N_i \equiv N_i(x,y)=(2A_{jk}+b_i x+a_i y)/2A, \qquad 2 A_{jk} \equiv x_j y_k - x_k y_j, \quad b_i \equiv y_j - y_k, \quad a_i \equiv x_k - x_j,$$

$$A \equiv \mbox{（三角形の面積）} = (a_2 b_1-a_1 b_2)/2 = (a_3 b_2-a_2 b_3)/2 = (a_1 b_3-a_3 b_1)/2$$ (B.8)

と定義した。ただし上式中の($i,j,k$)は(1,2,3)の偶置換とする。 三角形の面積を正の値として得るためには，図-B.1に 示したように，節点番号を反時計回りに(1,2,3)の順に捉える必要がある。

図 B.1: 定ひずみ三角形要素
図 B.2: 定ひずみ三角形要素の区分的多項式

変位関数$vect{u}$は線形であるから，一つの要素の辺に 沿っても変位は線形に変化する。また$\vect{q}$に節点の 変位成分を用いているから，相隣接する要素間の辺上でも変位そのものの 連続性が保証され，二つの要素が重なったり離れたりしないことがわかる。 ただし，変位の勾配（ひずみ）は要素内一定になり， 要素間では連続しないことになる。 このことから「定ひずみ三角形要素」 と呼ばれている。 変位関数$N_1$等を図-5.4で示した区分的多項式と 同じように，節点$n$を囲む四つの三角形要素上で定義された 区分的多項式$\phi_n(x,y)$として 図示したのが図-B.2である。 この四つの三角形要素中の任意の点の変位成分の大きさが この図の縦軸に比例しているようなものとして， 対象としている平面ひずみ問題の解を区分的に近似している。

B.2.2 剛性方程式

さて，式(B.2)の応力ひずみ関係は

$$\vect{\sigma}=\mat{C} \vect{\epsilon}$$ (B.9)

と表現できる。ここに

$$\mat{C} \equiv \dfrac{E}{(1+\nu)(1-2\nu)} \left( \begin{arr... ...\ \nu & 1-\nu & 0 \\ 0 & 0 & (1-2\nu)/2 \end{array}\right)$$ (B.10)

と定義した。また，ひずみ成分は式(3.6)の ひずみの定義から

$$\vect{\epsilon}=\mat{D} \vect{u}$$ (B.11)

と書くことができる。ここに

$$\mat{D} \equiv\left( \begin{array}{cc} \partial/\partial x ... ... \partial/\partial y & \partial/\partial x \end{array}\right)$$ (B.12)

と定義した。

式(B.9) (B.11)を仮想仕事式(B.3)に 代入し，式(B.6)の変位関数を代入して整理すると， 最終的に仮想仕事式は

$$\delta\vect{q}\supersc{t} \left[ \mat{k} \vect{q}-\vect{f}- \vect{g} \right]=0$$

と表され， この式が任意の仮想節点変位 $\delta\vect{q}$に 対して常に成立しなければならないことから， 平面ひずみ問題の剛性方程式 は

$$\vect{f}+\vect{g}= \mat{k} \vect{q}$$ (B.13)

となる。ここに

$$\vect{f} \equiv \int_S \mat{N}\supersc{t} \vect{F}\dint S,... ...} \mat{D}\supersc{t} \mat{C} \mat{D} \mat{N} \dint V$$ (B.14)

と定義した。$\mat{k}$が 剛性行列で，$\vect{f}$および$\vect{g}$は それぞれ要素の表面力および体積力の等価節点外力ベクトルである。

以上の関係式を用いれば，応力やひずみは

$$\vect{\epsilon}= \mat{D} \mat{N} \vect{q}, \quad \vect{\sigma}=\mat{C} \mat{D} \mat{N} \vect{q}$$

で求めることができる。また要素の厚さを$h$とする($V=Ah$)と，剛性行列 は

$$\mat{k}=\dfrac{hE}{4A(1+\nu)(1-2\nu)} \mat{\bar{k}}$$ (B.15)

と書け，$\mat{\bar{k}}$の 各要素は表-B.1に示した通りである。

表 B.1: 平面ひずみ問題に対する要素剛性行列

$\bar{k}_{11}=\bar{\alpha} b_1^2+\bar{\beta} a_1^2$	$\bar{k}_{12}=(\nu+\bar{\beta}) a_1 b_1$	$\bar{k}_{13}=\bar{\alpha} b_1 b_2+\bar{\beta} a_1 a_2$
$\bar{k}_{14}=\nu a_2 b_1+\bar{\beta} a_1 b_2$	$\bar{k}_{15}=\bar{\alpha} b_1 b_3+\bar{\beta} a_1 a_3$	$\bar{k}_{16}=\nu a_3 b_1+\bar{\beta} a_1 b_3$
$\bar{k}_{22}=\bar{\alpha} a_1^2+\bar{\beta} b_1^2$	$\bar{k}_{23}=\nu a_1 b_2+\bar{\beta} a_2 b_1$	$\bar{k}_{24}=\bar{\alpha} a_1 a_2+\bar{\beta} b_1 b_2$
$\bar{k}_{25}=\nu a_1 b_3+\bar{\beta} a_3 b_1$	$\bar{k}_{26}=\bar{\alpha} a_1 a_3+\bar{\beta} b_1 b_3$	$\bar{k}_{33}=\bar{\alpha} b_2^2+\bar{\beta} a_2^2$
$\bar{k}_{34}=(\nu+\bar{\beta}) a_2 b_2$	$\bar{k}_{35}=\bar{\alpha} b_2 b_3+\bar{\beta} a_2 a_3$	$\bar{k}_{36}=\nu a_3 b_2+\bar{\beta} a_2 b_3$
$\bar{k}_{44}=\bar{\alpha} a_2^2+\bar{\beta} b_2^2$	$\bar{k}_{45}=\nu a_2 b_3+\bar{\beta} a_3 b_2$	$\bar{k}_{46}=\bar{\alpha} a_2 a_3+\bar{\beta} b_2 b_3$
$\bar{k}_{55}=\bar{\alpha} b_3^2+\bar{\beta} a_3^2$	$\bar{k}_{56}=(\nu+\bar{\beta}) a_3 b_3$	$\bar{k}_{66}=\bar{\alpha} a_3^2+\bar{\beta} b_3^2$
$\bar{\alpha}\equiv 1-\nu$	$\bar{\beta}\equiv(1-2\nu)/2$

B.2.3 等価節点外力

図 B.3: 等価節点外力

式(B.14)第1, 2式の体積力と表面力の等価節点外力の値を， それぞれの外力成分が一様な場合に限って陽な結果を示しておく。 つまり$X_x$, $X_y$および

$$\vect{F^{\langle k\rangle}} \equiv \left\{ \begin{array}{c} ... ...langle k\rangle} \end{array}\right\} \quad\mbox{（$k$辺上で）}$$ (B.16)

として，すべての成分が一定であるとする。 ここの「$k$辺」とは，図-B.3に示したように 節点$k$に相対する辺を指す。 以上の条件下で式(B.14)第2, 3式を実際に計算すると

(B.17)

となる。式(B.17a)は，体積力の等価節点力が 要素内の総和($hA\vect{X}$)を三つの節点に 等分配されているに過ぎないことを示している。 一方式(B.17b)も，$k$辺に作用している 総表面力をその辺の両端の2節点に等分配しているだけである。

B.2.4 数値解析例と応力の精度

簡単な例題として，節-3.5.3で 取り上げた図-3.20の問題に 似た図-B.4(p.)の 系を有限要素解析してみよう。 この図の記号を用いれば$\ell=8$cm, $c=2$cmの領域（奥行1m）を 対象としており， 材料定数のうちYoung率は205GN/m$^2$, Poisson比は0.3とし， 分布外力は980kN/mとしている。 また端部の境界条件は式(3.130)の 条件ではなく，これも図-B.4の上図に示したように 変位が一箇所で固定された自由表面とした。 また，元の問題図-3.20(p.)は 左右対称な物体なので，図-B.4はその右半分だけを 解析対象にしている。したがって， 左辺での条件も図示したようになっている。

図 B.4: 定ひずみ三角形要素による解析例

求められた変位を1000倍に誇張して同図の中段に示した。 また下段には， 求められた応力分布と式(3.131)との比較図を示した。 応力の有限要素解は， 直応力$\sigma_{xx}$は同図上の左辺付近に縦に並ぶ八つの要素での値， せん断応力$\sigma_{xy}$は右辺付近の縦の8要素での値である。 定ひずみ要素だから，三角形の図心（図中の黒丸）での値であると 解釈することが多いので，式(3.131)の値もその位置に 対応した2断面毎に算定してプロットしてある。 ただし，直応力の場合は2断面での差が小さく重なってしまっている。 境界条件が若干異なっているが，定性的にはよく似た解を得， この程度の少ない要素分割数であることを考えると，定量的にも良い 結果が求められていると考えてよさそうだ。 このプログラム もまえがきに書いた方法で入手可能である。 例として図-B.4用のデータファイルも添付してある。

またこの文書での有限要素の定式化に従う限りは， 変位に近似関数を仮定した上で，その微係数で応力を求めている以上， 応力の近似度は変位のそれよりも劣る。 ここで定式化した定ひずみ要素の場合がその極端であり， 要素内で一定になる。したがって上述のように，この要素で求められる 応力は要素の重心における応力と解釈することが多い。 例えば図-5.7, 5.15, 5.29からも 明らかにように，構造部材の場合であっても応力の精度が変位の精度よりも悪い ことには，特に設計という観点からは十分に注意しなければならない。

最新版を正確に読むためには pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。