最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
前節では,仮想仕事の原理を古典的定義から近代的定義に まで改訂しながら近似解法としても捉え,その近似の精度が改善される 様を見てきた。ここでは,境界値問題の最も強力な 近似解法の一つである有限要素法 の基礎をその延長線上で概説する。
近似解法として弱形式の利用を考えた場合,前節の例でも
示したように,用いる弱形式と仮定する関数によって結果の精度が左右される。
工学的に許容できる範囲内で近似解を得るためにも,この精度を
上げる方法を考えておく必要がある。
前節では基本的に弱形式の関数![]() に,
問題の定義域全体で定義された一つの関数
に,
問題の定義域全体で定義された一つの関数![]() (前節では
(前節では![]() )を
用いて
)を
用いて
![]() という
近似表現を用いていたが,その精度をあげるためには
という
近似表現を用いていたが,その精度をあげるためには
の二つの方法を思い付くだろう。つまり,例えば後者の場合は
のように複数の関数を用いて複数の未知定数![]() を決めるようにし,
この項数
を決めるようにし,
この項数![]() を増やすことによって精度の改善が期待される。
選点法なら,領域中に
を増やすことによって精度の改善が期待される。
選点法なら,領域中に![]() 個の点
個の点![]() (
(![]() )を選び,
つまり重みを
)を選び,
つまり重みを
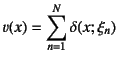 として
重みつき残差法を用いてそこの誤差を零にする条件を求めれば,
それが
として
重みつき残差法を用いてそこの誤差を零にする条件を求めれば,
それが![]() 個の
個の![]() (
(![]() )に対する連立方程式になるので,
それを解けばいい。
)に対する連立方程式になるので,
それを解けばいい。
では式(5.10)の仮想仕事式を
用いた例を一つ解いてみよう。前節で対象とした等分布外力の作用した
単純梁(5.1)を,例えば前節で
用いた二つの近似関数を利用して
と仮定してみる。
上式中の二つ目の関数は厳密解に近い関数式(5.5)である。
仮想変位は,未知定数が少し変動したものと解釈すればよかったから
と置ける。この二つを仮想仕事式(5.10)に 代入して整理すると
![\begin{eqnarray*}
&& EI\int_0^\ell
\left[-2 a_1+a_2 (-2\ell^2-12\ell x+12x^2)\r...
...x)
+\delta a_2 x(\ell-x)(2\ell^2+\ell x-x^2)\right] \dint x = 0
\end{eqnarray*}](s2img115.gif)
となる。各項毎の積分を実行すると
とまとめられる。任意の![]() ,
, ![]() に対してこの
等式が常に成立するためには,それぞれの鈎括弧の部分が同時に
零になればいい。すなわち
に対してこの
等式が常に成立するためには,それぞれの鈎括弧の部分が同時に
零になればいい。すなわち
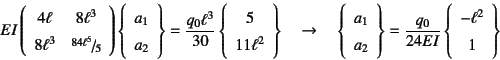
と求められる。実はこの![]() ,
, ![]() を代入した
を代入した![]() は厳密解に一致する。
すなわち,近似解法とは言え厳密解を含む関数の集合の中で近似をすると,
きちんと厳密解を得ることができることを示している。このことからも,
式(5.9)の誘導過程で示したように,
仮想仕事の原理が元の境界値問題とある意味で等価なことがわかる。
は厳密解に一致する。
すなわち,近似解法とは言え厳密解を含む関数の集合の中で近似をすると,
きちんと厳密解を得ることができることを示している。このことからも,
式(5.9)の誘導過程で示したように,
仮想仕事の原理が元の境界値問題とある意味で等価なことがわかる。
上式のたわみの代わりに,
もし![]() の方の近似解に中央に集中外力を受ける単純梁の
たわみを用いたとしても,
の方の近似解に中央に集中外力を受ける単純梁の
たわみを用いたとしても,
![]() 点でのたわみの近似解と
厳密解の誤差は1.8%に留まっている。
さらに驚くべきことに,
梁中央部のたわみ
点でのたわみの近似解と
厳密解の誤差は1.8%に留まっている。
さらに驚くべきことに,
梁中央部のたわみ
![]() は厳密解に一致するが,
その様子については次の節で具体的に示す。
は厳密解に一致するが,
その様子については次の節で具体的に示す。
式(5.11)では暗黙のうちに,対象としている全領域を
その定義域とする滑らかな関数![]() を複数用いることにして,
精度を上げる方法について提案しているように見える。
しかし,最後の例の中央に集中荷重が作用した梁のたわみを用いた
場合は3階の微係数が不連続な関数を用いたことになるが,
それでも高い精度の近似解が得られている。このようなことを考えると,
もう一つの改善策として「対象とした領域を多くの区間に分割し,
関数はある程度までの連続性しか持たない(多項式の次数が低い等)まま,
各区間毎に区分的に定義された関数を用いて近似する」というアイデアは
どうだろう? 例えば,
柱の
を複数用いることにして,
精度を上げる方法について提案しているように見える。
しかし,最後の例の中央に集中荷重が作用した梁のたわみを用いた
場合は3階の微係数が不連続な関数を用いたことになるが,
それでも高い精度の近似解が得られている。このようなことを考えると,
もう一つの改善策として「対象とした領域を多くの区間に分割し,
関数はある程度までの連続性しか持たない(多項式の次数が低い等)まま,
各区間毎に区分的に定義された関数を用いて近似する」というアイデアは
どうだろう? 例えば,
柱の![]() 方向の変位成分
方向の変位成分![]() の場合には,図-5.4に
示したように,関数
の場合には,図-5.4に
示したように,関数![]() が点
が点![]() で1になる
ように,かつ限られた領域
で1になる
ように,かつ限られた領域
![]() 上だけで
定義された1次多項式として
上だけで
定義された1次多項式として
と近似するのである。
また,式(5.11)の未知定数![]() の代わりに,
の代わりに,![]() における
未知関数そのものの値
における
未知関数そのものの値![]() を未知定数としていることに注意して欲しい。
を未知定数としていることに注意して欲しい。
一つ例を解いてみよう。等分布外力と先端に集中外力が
作用する図-5.5の柱を対象とする。
区分的に与える近似関数を
と置いてみる。ここに用いた関数は図-5.5の右側に
示したように
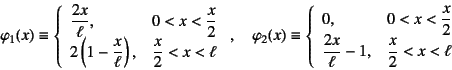
と,区分的1次多項式で与えた。一方,仮想仕事式は梁と同様の演算により
となるから,式(a)を代入すれば
を得るから,結局,具体的に関数を代入して積分を実行すると
となる。
したがって,任意の![]() に対してこの式が常に
成立するためには,上式の鈎括弧内がいずれも同時に零であればよく
に対してこの式が常に
成立するためには,上式の鈎括弧内がいずれも同時に零であればよく
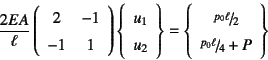
を満足しなければならない。したがって,これを解くと答が
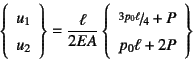
となる。
結果を図-5.6に破線で示したが,
変位![]() の厳密解が2次関数であるのに対し,それに
非常に近い折れ線で近似解が求められている。
また変位には1次多項式を選んだから,
変位
の厳密解が2次関数であるのに対し,それに
非常に近い折れ線で近似解が求められている。
また変位には1次多項式を選んだから,
変位![]() の1階の微係数である軸力
の1階の微係数である軸力![]() は定数になり,
それが厳密解の平均値になっていることも図からわかる。
つまり,軸力が最小2乗法
的に求められた近似解になっているように見える。
は定数になり,
それが厳密解の平均値になっていることも図からわかる。
つまり,軸力が最小2乗法
的に求められた近似解になっているように見える。
さらに精度を上げるには,関数の形はこのままにして区分けを
多くしていけばよさそうである。図-5.7に4区分
した場合の近似解を示したが,これから類推できるように,
区分数を増やすことによって近似解は次第に厳密解に漸近していき,
その極限として厳密解に「収束
する」と考えてよさそうだ。
ただ変位については,上で求められた![]() は厳密解に一致している。
関数が近似であるにもかかわらず,係数として選んだ未定定数が
厳密解に一致しているのは,前節で示した例と同じである。
何故厳密解が得られるかという
理由の一つは節-5.4.1に示した。
このように,区分数を増やすことに伴う近似解の厳密解への
収束が一様ではなく,ある点だけで厳密解に一致する現象は超収束
と呼ばれる[70]が,これが発生するのはごく稀であり,
あくまでも区分的多項式による解は近似であると
認識しておく必要がある。
は厳密解に一致している。
関数が近似であるにもかかわらず,係数として選んだ未定定数が
厳密解に一致しているのは,前節で示した例と同じである。
何故厳密解が得られるかという
理由の一つは節-5.4.1に示した。
このように,区分数を増やすことに伴う近似解の厳密解への
収束が一様ではなく,ある点だけで厳密解に一致する現象は超収束
と呼ばれる[70]が,これが発生するのはごく稀であり,
あくまでも区分的多項式による解は近似であると
認識しておく必要がある。
以上のように,区分的な多項式で近似しても精度が上げられることを
示すことができた。
それぞれの有限な区間![]() の領域を有限要素
と呼ぶことにして,
例えば図-5.5の
の領域を有限要素
と呼ぶことにして,
例えば図-5.5の
![]() の
有限要素に着目してみよう。すると,そこでは
の
有限要素に着目してみよう。すると,そこでは
といったような近似をしていることがわかる。 このような近似解法を有限要素法 と呼んでいる。 要素数を増やすことによって近似解は
ことが期待できる。 この有限要素法の考え方は,区分的多項式 と弱形式を組み合わせた 境界値問題の近似解法であり,例えば,拡散や浸透流の問題や 波動方程式のようなものにも同じように適用できる汎用的な 近似解法である。