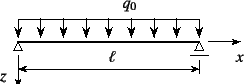 |
最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
節-4までに,梁や柱の境界値問題をきちんと微分方程式で 記述して解く方法をいくつか紹介してきた。 例えば図-5.1のような単純な梁であれば, 影響線載荷による断面力や応力分布を求めることにはさほどの困難は無く, 断面を設計することもできることを示してきた。 しかし構造が大きく立体的になるにつれて,そのような微分方程式や 後述の仮想仕事的・エネルギ的手法を用いた解析的手法は 非現実的であることも容易に推測できると思う。
ところで同時に,構造力学はいろいろな仮定が含まれる近似力学だと述べてきた。 また構造設計においては,不確定要因による危険を避けるために安全率 あるいはそれに準じたパラメータを用いて,一種の余裕のある構造設計をしている。 それならば,含まれる誤差の程度が明らかな近似的な手法で支配方程式を 解いても,十分な安全が確保できることが期待される。 そこでこの章では,最も代表的で有用な有限要素法について説明する。
理解を容易にするために図-5.1の例を用いて
説明しよう。章-4のたわみで表した棒理論の支配方程式を
用いてこの図の問題に対する基礎式を列挙すると,
つり合い式が
| (5.1) |
であり,境界条件が
| (5.2) |
となる。この解を,ある既知関数![]() と
未知定数
と
未知定数![]() を用いて
を用いて
![]() で近似できるものとして,
式(5.1)等ができるだけ満足されるように最も適切な
定数
で近似できるものとして,
式(5.1)等ができるだけ満足されるように最も適切な
定数![]() を決定する方法について考えてみよう。
もちろん,
を決定する方法について考えてみよう。
もちろん,
![]() は正解ではないから
は正解ではないから
は必ずしも零にはならないが,
この式(a)の![]() は近似解
は近似解
![]() の持つ
一種の誤差と考えていい。
もちろん境界条件も必ずしも満足していないからそこにも誤差が存在するが,
それはまだ式(a)には含まれていないことに注意する。
精度の高い近似解は,この誤差をできるだけ小さくすることによって
求められそうだ。
の持つ
一種の誤差と考えていい。
もちろん境界条件も必ずしも満足していないからそこにも誤差が存在するが,
それはまだ式(a)には含まれていないことに注意する。
精度の高い近似解は,この誤差をできるだけ小さくすることによって
求められそうだ。
例えば最も簡単な近似法の一つとして,![]() の間の
ある特定の点を選んで,そこだけで式(a)の
誤差を零にするように近似解を探すということが考えられる。
つまり,例えばスパン中央点で
の間の
ある特定の点を選んで,そこだけで式(a)の
誤差を零にするように近似解を探すということが考えられる。
つまり,例えばスパン中央点で
のように![]() を決定することができる。これは選点法
と呼ばれている。
もちろん
を決定することができる。これは選点法
と呼ばれている。
もちろん![]() は4階微分が可能であり,
は4階微分が可能であり,
![]() での
値
での
値
![]() が零でないものとする。
が零でないものとする。
あるいは,梁全体![]() で平均的に誤差を小さくするように,
最小2乗法
を適用して
で平均的に誤差を小さくするように,
最小2乗法
を適用して
としてみよう。つまりこの2乗誤差が![]() に関して最小になるように
に関して最小になるように
![\begin{displaymath}
\to \quad \int_0^\ell \bigl[-EI a \psi''''(x)+q_0\bigr]
...
...splaystyle \int_0^\ell EI\{\psi''''(x)\}^2 \dint x}
\eqno{(c)}
\end{displaymath}](s2img50.gif)
によって![]() を決定してもいいかもしれない。
ここでは
を決定してもいいかもしれない。
ここでは![]() は4階の微係数が存在すればいい。ところで,
この式(c)の最後から二つ目の式の左辺は,式(a)で定義した
誤差
は4階の微係数が存在すればいい。ところで,
この式(c)の最後から二つ目の式の左辺は,式(a)で定義した
誤差![]() に
に
![]() の重み
を乗じた上で,全スパン合計した平均的な誤差と解釈できる。
そこで,これを一般化すると,ある任意の重み
の重み
を乗じた上で,全スパン合計した平均的な誤差と解釈できる。
そこで,これを一般化すると,ある任意の重み![]() を用いて
を用いて
| (5.3) |
のように,誤差の全領域重みつき平均を零にするような方法が,
最小2乗法を一般化した近似法(重みつき残差法
)だと解釈してもいいだろう。
つまり上の最小2乗法は,重み![]() として
として
を選んだことになる。
この場合の重み![]() の物理的な意味を無理やり考えてみると,
それは
の物理的な意味を無理やり考えてみると,
それは![]() 方向の総内力になっている。
このように考えると,実は
式(b)の選点法も,同じ重みつき残差法的な
近似式(5.3)に
おいて重み
方向の総内力になっている。
このように考えると,実は
式(b)の選点法も,同じ重みつき残差法的な
近似式(5.3)に
おいて重み![]() に式(4.55)で定義したデルタ関数を用いて
に式(4.55)で定義したデルタ関数を用いて
と置いたものとして認識できる。これを物理的に解釈するのはちょっと難しい。
さて計算するまでもなく,同じ近似解
![]() を用いた場合,
最小2乗法の方が,1点を用いた選点法よりも
精度のいい解を得ることができそうだ。
つまり,ほとんどすべての近似法は式(5.3)で
表現できそうだが,その近似の精度は選んだ関数
を用いた場合,
最小2乗法の方が,1点を用いた選点法よりも
精度のいい解を得ることができそうだ。
つまり,ほとんどすべての近似法は式(5.3)で
表現できそうだが,その近似の精度は選んだ関数![]() だけでなく
重み
だけでなく
重み![]() にも強く依存しそうである。
にも強く依存しそうである。
では次に,より精度の高い解を求めることを目標として,
この式(5.3)を別の角度から
解釈し直してみよう。
まず式(5.1)左辺は任意の微分
要素![]() に作用している
に作用している![]() 方向の力(内力および外力)の総和である。
つり合っているならそれは零になる。
そこで重み
方向の力(内力および外力)の総和である。
つり合っているならそれは零になる。
そこで重み![]() を
を![]() 方向の何らかのたわみだと解釈し,
この微分要素をさらに
方向の何らかのたわみだと解釈し,
この微分要素をさらに![]() だけ
だけ![]() 方向に仮想的に移動させたとすると,
この微分要素に作用している力は次式の大きさの仮想的な仕事をする。
方向に仮想的に移動させたとすると,
この微分要素に作用している力は次式の大きさの仮想的な仕事をする。
もし系がつり合っていれば式(5.1)が成り立つから,
この
![]() はいたるところで零であり,
上式の仕事も零になる。
したがって,この仮想的な仕事を
はいたるところで零であり,
上式の仕事も零になる。
したがって,この仮想的な仕事を![]() から
から![]() まで積分して
全領域で総和をとった総仕事もやはり零である。
つまり,
まで積分して
全領域で総和をとった総仕事もやはり零である。
つまり,![]() が
が![]() におけるつり合いを満足する解で
ある限り,任意の仮想的な変位
におけるつり合いを満足する解で
ある限り,任意の仮想的な変位![]() に対して
に対して
| (5.4) |
が成立する。
これが式(5.3)であり,
初等的な仮想仕事の原理と呼んでもいい。
そのような呼び名はどうでもいいのだが,他と区別するために,
この形式を古典的なGalerkin形式
と呼ぶことにし,式(5.1) (5.2)で表される境界値
問題の弱形式
の一つの表現と称する。
もちろん,近似解法のことだけを考えて式(5.3)を
捉えるなら,最小2乗法や選点法のように![]() が「変位」である必要も無く,
この式の意味を物理的な「仕事」という概念を通して考える必要も無い。
つまり,上式(5.4)は純粋に数学的な表現に
過ぎないと言ってもいい。
が「変位」である必要も無く,
この式の意味を物理的な「仕事」という概念を通して考える必要も無い。
つまり,上式(5.4)は純粋に数学的な表現に
過ぎないと言ってもいい。
ところで,もし![]() が元の問題の
正解であれば式(5.1)がすべての点
が元の問題の
正解であれば式(5.1)がすべての点![]() で厳密に成立する。
つまり,式(5.1)は
で厳密に成立する。
つまり,式(5.1)は![]() を決定するための
非常に「強い」条件(つり合い式;強形式
)として捉えられる。
これに対して上の式(5.4)を「弱い形式」と呼ぶのは,
任意の関数
を決定するための
非常に「強い」条件(つり合い式;強形式
)として捉えられる。
これに対して上の式(5.4)を「弱い形式」と呼ぶのは,
任意の関数![]() に対して
式(5.4)を満足する
に対して
式(5.4)を満足する![]() が必ずしも
元の境界値問題の正解ではないからである。
しかしこの
が必ずしも
元の境界値問題の正解ではないからである。
しかしこの![]() が正解でなかったとしても,
上の式(5.3)でも示したように
「式(5.4)の被積分関数の
括弧の中は正解ではない
が正解でなかったとしても,
上の式(5.3)でも示したように
「式(5.4)の被積分関数の
括弧の中は正解ではない![]() によって生じた不つり合い力
すなわち誤差であり,
それに重み
によって生じた不つり合い力
すなわち誤差であり,
それに重み![]() を乗じて梁全体でその誤差の総和をとったものが
零になる」ということを示していることから,
誤差の平均が最小2乗法的に零になっている条件として
式(5.4)を捉えられそうだ。
したがって弱形式を用いれば,
を乗じて梁全体でその誤差の総和をとったものが
零になる」ということを示していることから,
誤差の平均が最小2乗法的に零になっている条件として
式(5.4)を捉えられそうだ。
したがって弱形式を用いれば,![]() の近似解を求めることができそうだと
期待できる。
ただここまでのアプローチにおける大きな問題点は,基礎となる
弱形式の中に境界条件が全く考慮されていない点である。
この境界条件に対する配慮については節-5.1.2
(3)で示すが,そのアプローチからは,
この弱形式が「仕事」という観点で捉えられている必要があることが
明らかである。そのような意味で,上では「弱形式は純粋に
数学的な表現」であるとは述べたが,実際には「弱形式は頭の中だけで
物理的にかつ仮想的に考える仕事の原理」であると理解した方がいいだろう。
あるいは,その方が理解し易い人が多いと思われる。
の近似解を求めることができそうだと
期待できる。
ただここまでのアプローチにおける大きな問題点は,基礎となる
弱形式の中に境界条件が全く考慮されていない点である。
この境界条件に対する配慮については節-5.1.2
(3)で示すが,そのアプローチからは,
この弱形式が「仕事」という観点で捉えられている必要があることが
明らかである。そのような意味で,上では「弱形式は純粋に
数学的な表現」であるとは述べたが,実際には「弱形式は頭の中だけで
物理的にかつ仮想的に考える仕事の原理」であると理解した方がいいだろう。
あるいは,その方が理解し易い人が多いと思われる。
では,とりあえず
式(5.4)を用いて実際に近似解を求めてみよう。
式(5.2)の境界条件を念頭に置いて,
もし![]() を未知定数とした近似解を
を未知定数とした近似解を
と仮定すると,まずは規定された四つの境界条件を満足する。
そこで重み![]() にも
にも
![]() のように
同じ関数を用いて式(5.4)に代入することによって,
未知数
のように
同じ関数を用いて式(5.4)に代入することによって,
未知数![]() を決めてみよう。すると
を決めてみよう。すると
となるから,結局
と求められる。この問題の中央点での
たわみの厳密解は
![]() で
あるから,上の近似関数で同点のたわみの近似値を計算すると
で
あるから,上の近似関数で同点のたわみの近似値を計算すると
となり,約0.4%の誤差しか持たない精度のとてもいい近似解であることがわかる。
このように弱形式を用いて求められる解は,元の問題の 近似解になっており,近似する関数を適切に選べば, この例のように良好な精度で解を求めることができそうだ。 ただ注意しなければならないのは,ここでsine関数を 選んだことである。この選択によって,近似関数は四つすべての 境界条件を満足しており, 誤差はつり合い式のみに存在していることになる。 だから,解の精度を高めることができたのではないだろうか。
試しに,厳密なたわみの解の式(4.34)を少し変形した
を用いてみよう。下線を引いた`2'だけが厳密解と異なっている。
この関数は両端で零になり幾何学的境界条件は満足するが,
その2階の微係数は両端で零にはならず,
式(5.2)の境界条件のうちの力の境界条件は満足していない。
式(5.5)の![]() の無い右辺を
の無い右辺を![]() として用い,
上と同様の演算を実行してみると
として用い,
上と同様の演算を実行してみると
となり,中央のたわみは 厳密解の1.8倍,つまり80%もの誤差を含んでしまう。 したがって,式(5.4)の古典的なGalerkin形式を使う限りは, 当然のことながら, 幾何学的境界条件を満たしてはいるが力学的境界条件を満たさない 近似解(5.5)を用いた場合には,解には大きな 誤差を含んでしまう。 これではとても実用的な近似解法とは呼べそうもない。
となる。ここに![]() はデルタ関数で,節-4.4.1の
式(4.55)で
その定義と扱い方を示してある。この問題の弱形式を
求めよ。
はデルタ関数で,節-4.4.1の
式(4.55)で
その定義と扱い方を示してある。この問題の弱形式を
求めよ。
上の最後の例では,一部の境界条件(力学的境界条件)に 誤差を含む関数を選んだために, 式(5.4)を用いて得た近似解の精度が悪くなったと考えられる。 より複雑な問題では,すべての境界条件を満たす近似関数を 探すのが困難な場合が普通であり,このままでは弱形式(5.4)は 使えそうもない。 また,近似関数は4階の微係数が定義できるものでないといけなかったことも 思い出して欲しい。 これを改善するためには境界条件の誤差も含めた 弱形式を定義し直せばよく,同時に近似関数の微係数の階数も 小さくできれば便利だろう。 そこで,弱形式(5.4)に境界条件式(5.2)の 一部を含めることを試みよう。
まず重み
関数![]() には最低限2階微分可能なものを選ぶことにして,
式(5.4)の被積分関数第1項を2回部分積分してみよう。
すると
には最低限2階微分可能なものを選ぶことにして,
式(5.4)の被積分関数第1項を2回部分積分してみよう。
すると
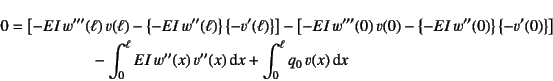
となる。さらに重みとして用いる関数![]() は,少なくとも
元の問題の幾何学的境界条件は満足し
は,少なくとも
元の問題の幾何学的境界条件は満足し
となるものを選ぶ5.1ことにする。
これと式(5.2)のうちの力の境界条件とを
上式右辺第1行目に代入すると,そのすべてが零になり,最終的に上式は
となる。
式(5.6)は一見境界における項を含まず,式(5.4)と
何ら変わりがないように見える。
しかしその誘導過程で明らかなように,もし重みの関数![]() と
近似関数の両方に,幾何学的境界条件を満足して2回微分可能な
(2階の微係数が定義できる)関数を用いれば,
上の演算が示すように,
元の問題の力学的境界条件を何らかの意味で式(5.4)に
加味した弱形式が誘導されている可能性があり,
それが近似に使えると期待できそうだ。
この力学的境界条件を考慮した弱形式(5.6)をGalerkin形式
と呼んでいる。
あるいは,古典的なGalerkin形式(5.4)の誘導過程
からもわかるように,仮想仕事式
という物理的な名称で呼ばれることが多い。
と
近似関数の両方に,幾何学的境界条件を満足して2回微分可能な
(2階の微係数が定義できる)関数を用いれば,
上の演算が示すように,
元の問題の力学的境界条件を何らかの意味で式(5.4)に
加味した弱形式が誘導されている可能性があり,
それが近似に使えると期待できそうだ。
この力学的境界条件を考慮した弱形式(5.6)をGalerkin形式
と呼んでいる。
あるいは,古典的なGalerkin形式(5.4)の誘導過程
からもわかるように,仮想仕事式
という物理的な名称で呼ばれることが多い。
では新しく誘導された弱形式を用いて近似解を求めてみよう。
比較のために式(5.5)で示した4次多項式で![]() を
近似し,重み
を
近似し,重み![]() も同じく式(5.5)から
も同じく式(5.5)から![]() を
取り除いた部分で与える。
微分を2回だけすれば,あとの演算は前の近似と同様である。
繰り返すが式(5.5)は力学的境界条件を満足していない。
これを式(5.6)に代入して,
未知係数
を
取り除いた部分で与える。
微分を2回だけすれば,あとの演算は前の近似と同様である。
繰り返すが式(5.5)は力学的境界条件を満足していない。
これを式(5.6)に代入して,
未知係数![]() と中央点でのたわみを計算すると
と中央点でのたわみを計算すると
となる。つまり,前の方法では80%もの誤差を出したのと同じ関数を 近似解として用いたにもかかわらず,新しく拠りどころにした 式(5.6)の弱形式を用いると, その誤差をわずか5.7%にまで小さくできた。 この式(5.6)のGalerkin形式を用いた近似解法をGalerkin法 と呼んでいる。 ちなみに,前の古典的なGalerkin法では厳密解よりも大きい近似解になっていたが, ここで得たGalerkin法の解は厳密解よりも小さい解になっている。 これはGalerkin法がエネルギ的な手法と何らかの関係があるためであるが, 興味のある読者は参考書を読んで欲しい。
再度Galerkin形式の誘導過程と最終的な表現を見直してみると,![]() の
近似関数と重み
の
近似関数と重み![]() については
については
ことがわかる。そこで上の例よりもっと簡単な関数で試してみよう。
もちろん厳密解は![]() の4次多項式ではあるが
の4次多項式ではあるが
と置いてみよう。図示する限りは2次多項式と4次多項式は
それほどの違いは無いだろう。
しかし2階の微係数が零ではなく定数になるので
力学的にはとんでもない近似であるが,
少なくとも積分は簡単になる。
これを式(5.6)のGalerkin形式に代入し,
未知係数![]() と中央点のたわみを計算すると
と中央点のたわみを計算すると
となる。つまり4次多項式を2次の多項式で近似したにも かかわらず,中央点でのたわみの誤差はわずか10%程度に 留まっている。 上述のように,2次多項式の2階の微係数は定数になり, したがって曲げモーメントの近似解は全スパン一定になり, 明らかに力学的境界条件も満足しておらず, 物理的にはとてもおかしな解であるが, この変位そのものの精度は非常にいいのではないだろうか。 以上の結果をたわみ形状で比較したのが図-5.2である。 破線が先に求めた4次多項式の場合の答であり, 実線が2次多項式の近似解である。
もう少し力の境界条件の取り扱い方が
わかり易くなるような例題として,図-5.3に
示したように分布外力が一様ではなく,右端にも
集中外力モーメントが作用して零でない力学的境界条件を有する系を
対象にしておこう。この場合も前節と同様の演算を繰り返すことに
よって,最終的なGalerkin形式が
となる。
外力![]() ,
, ![]() が作用してたわんだ状態の梁にさらに加えた
仮想的なたわみの乱れが
が作用してたわんだ状態の梁にさらに加えた
仮想的なたわみの乱れが![]() であると解釈していたことを思い出して,
各項の物理的解釈をしよう。
式(4.13b)の曲げモーメントと曲率の関係を
考慮すると,第1項は内力曲げモーメント
であると解釈していたことを思い出して,
各項の物理的解釈をしよう。
式(4.13b)の曲げモーメントと曲率の関係を
考慮すると,第1項は内力曲げモーメント
![]() が
仮想的な曲率の乱れ
が
仮想的な曲率の乱れ
![]() とする
仮想的な仕事の総和になっている。
また,第2項は分布外力
とする
仮想的な仕事の総和になっている。
また,第2項は分布外力![]() のする仮想的な外力仕事,さらに
最後の項は端外力モーメント
のする仮想的な外力仕事,さらに
最後の項は端外力モーメント![]() がたわみ角の乱れ
がたわみ角の乱れ
![]() と
する端部での仮想的な外力仕事である。
以上の結果から,上の弱形式は「内力の仮想仕事から外力の
仮想仕事を引いたものは零になる」ことを示した式であり,
このGalerkin形式のことを(力学以外の問題5.2で
あっても)仮想仕事の式あるいは仮想仕事の原理
と呼ぶことが多い。
と
する端部での仮想的な外力仕事である。
以上の結果から,上の弱形式は「内力の仮想仕事から外力の
仮想仕事を引いたものは零になる」ことを示した式であり,
このGalerkin形式のことを(力学以外の問題5.2で
あっても)仮想仕事の式あるいは仮想仕事の原理
と呼ぶことが多い。
近似計算の部分を除きここまでは,![]() が厳密解であることを
前提にして定式化をしてきた。
今度は逆に,
が厳密解であることを
前提にして定式化をしてきた。
今度は逆に,![]() は幾何学的境界条件を満足した2階微分可能な
関数とし,
は幾何学的境界条件を満足した2階微分可能な
関数とし,![]() の代わりに,幾何学的境界条件を満足し4階微分可能な
関数
の代わりに,幾何学的境界条件を満足し4階微分可能な
関数![]() を考えよう。このとき任意の
を考えよう。このとき任意の![]() に対して
に対して![]() が
が
を満足している場合に,弱い意味でいかなる方程式を![]() は満足して
いるのかということを誘導しておこう。
ただし
は満足して
いるのかということを誘導しておこう。
ただし![]() は前より少し条件をゆるめ
は前より少し条件をゆるめ
ものとする。ただこの例では幾何学的境界条件は零境界条件なので,
それを![]() も満たせばいい。
さて,前節までの演算とは逆向きの演算をすればいいので,
この式の第1項を
も満たせばいい。
さて,前節までの演算とは逆向きの演算をすればいいので,
この式の第1項を![]() の方に対して2回部分積分すると
の方に対して2回部分積分すると
となる。![]() が幾何学的境界条件を規定した境界で零になることを
右辺第1項に代入して整理すると
が幾何学的境界条件を規定した境界で零になることを
右辺第1項に代入して整理すると
となる。ここで,任意の![]() つまり仮想的にどんな乱れを与えたとしても,
この式が常に成立するためには,まず第1項の
つまり仮想的にどんな乱れを与えたとしても,
この式が常に成立するためには,まず第1項の![]() の係数が
零であると同時に,第2項の被積分関数の
の係数が
零であると同時に,第2項の被積分関数の![]() の係数の
括弧の中が物体中のすべての場所で零であればいいことがわかる。つまり
この式は,
の係数の
括弧の中が物体中のすべての場所で零であればいいことがわかる。つまり
この式は,![]() が
が
を満足するための必要条件になっていることがわかる。すぐわかるように,
この二つの式はそれぞれ,![]() でのつり合い式と
でのつり合い式と![]() での力学的
境界条件に他ならない。
での力学的
境界条件に他ならない。
この誘導から,適切に選んだ関数![]() が仮想仕事の
原理を満足していれば,それは最終的につり合い式および
力学的境界条件を上のような弱い(積分された平均的な)意味で
満足するように仕組まれていることがわかる。
また幾何学的境界条件を
が仮想仕事の
原理を満足していれば,それは最終的につり合い式および
力学的境界条件を上のような弱い(積分された平均的な)意味で
満足するように仕組まれていることがわかる。
また幾何学的境界条件を![]() は
満足していなければならず,
は
満足していなければならず,![]() も
その幾何学的境界条件に対応した零境界条件を満足していなければ
ならないことが明らかである。古典的なGalerkin形式に基づく
近似では,幾何学的なものだけではなく力学的な境界条件も
満足する関数を用いなければ精度が
上げられなかった。これに対しGalerkin形式を用いた近似では,
力学的境界条件を満足しない関数を用いたとしても,ある程度の
精度で近似解が求められたが,その理由は上のような仕組みがあるからである。
通常,幾何学的境界条件を本質的境界
条件,力学的境界条件を自然境界条件
と呼んで区別している。
も
その幾何学的境界条件に対応した零境界条件を満足していなければ
ならないことが明らかである。古典的なGalerkin形式に基づく
近似では,幾何学的なものだけではなく力学的な境界条件も
満足する関数を用いなければ精度が
上げられなかった。これに対しGalerkin形式を用いた近似では,
力学的境界条件を満足しない関数を用いたとしても,ある程度の
精度で近似解が求められたが,その理由は上のような仕組みがあるからである。
通常,幾何学的境界条件を本質的境界
条件,力学的境界条件を自然境界条件
と呼んで区別している。
さて近似解は,前節までと同様
![]() と仮定して
式(5.8)を満足するように
と仮定して
式(5.8)を満足するように![]() を求めれば得られるはずだ。
ところで上式(5.8)を仮想仕事の式と呼んだ。
つまり
を求めれば得られるはずだ。
ところで上式(5.8)を仮想仕事の式と呼んだ。
つまり![]() はつり合っている状態に仮想的に加えた乱れの変位と
呼んでいたが,これを仮想変位
と呼ぶことにして,
はつり合っている状態に仮想的に加えた乱れの変位と
呼んでいたが,これを仮想変位
と呼ぶことにして,![]() にさらに加えた量なので
にさらに加えた量なので![]() と書くことにする。
こうすれば式(5.8)は
と書くことにする。
こうすれば式(5.8)は
と表現できる。このように考えると,![]() に対しては
に対しては
![]() と置けばいいことになる。
つまり上式(5.10)は
と置けばいいことになる。
つまり上式(5.10)は
となり,任意の仮想変位,
つまり任意の![]() に対してこの式が成立する条件から
に対してこの式が成立する条件から
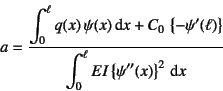
のように解が求められる。
実際の精度については各自![]() に適当な関数を用いて確かめて欲しい。
に適当な関数を用いて確かめて欲しい。