sec5

ケーブル等は微小ひずみで弾性のまま巨視的には大きく変位・変形する。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... と呼ぶ ^12.2

本当はこの配置を基準配置と呼ぶのであるが，この文書で最も重要なupdated Lagrange的アプローチ(p.

)を説明するために，初期配置と称することにした。多くの読者はこれを基準配置と呼ぶ方がいいかもしれない。また`updated'に対応させて，一般には普通のLagrange的アプローチを`total Lagrange'的と称するが，この文書では簡単のために`total'を付けていない。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... 限らない ^12.3

例えば，ひずみ尺度のテンソル成分が無次元でなかったり，応力のテンソル成分が非対称でかつ成分同士が直交していなかったりする。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...運動 ^12.4

「運動」は`kinematics'の直訳であり，動的な要素を重視した概念ではない。また`dynamics'は動力学であり，つり合い`statics'も含んでいる。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...のび@伸び ^12.5

`elongation'という単語も「伸び」と訳されるが，異なる定義である上にひずみの尺度ではないので注意する。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...という関係が定義できる ^12.6

本当かな?変形履歴に依存する非可逆な塑性変形があったら?

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... 我々が直感的・物理的 ^12.7

数学的には，お互いの関係がわかっている量ならどれでも構わないのだが。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... 変化率 ^12.8

実は変形の変化率のほとんどはupdated Lagrange的な量であるような気がする。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... スピン ^12.9

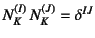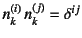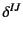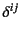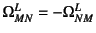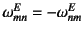$N_K^{(I)} N_K^{(J)}=\delta^{IJ}$ , $n_k^{(i)} n_k^{(j)}=\delta^{ij}$ と定義している（ $\delta^{IJ}$ と $\delta^{ij}$ もKronechkerのデルタ）ことからスピンの反対称性 $\Omega^L_{MN}=-\Omega^L_{NM}$ , $\omega^E_{mn}=-\omega^E_{nm}$ を示すことができる。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... これはよく乗算則（乗算分解）^12.10

Asaro[4]の論文を元にしたようだが，Asaroは結晶金属の弾塑性変形の概念について乗算則で説明しているが，実際にはこの節のような加算則の説明をしているだけだと思うのだが。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...となる ^12.11

流れ則が積分できないことは，ここでは知らなかったことにする。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... 同じ ^12.12

特に有限変形の教科書では，これが逆のものの方が多いような印象を持つので十分注意すること。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... が定義 ^12.13

ほとんどすべての文献（例えば[51]）では，このnominal応力を第1 Piola-Kirchhoff応力と呼んでいる。実際，文献[59]の定義とその著者による1980年頃の講義ノートの中の定義も逆になっているが，ここでは，この二つの応力が最初に定義された参考文献を明示している文献[59]の方の定義を用いた。nominal応力という呼び方は文献[33]にあるようで，後述の第1 Piola-Kirchhoff応力を定義して命名したのは文献[75,76]となっている。多くの読者は，このnominal応力を第1 Piola-Kirchhoff応力と呼んだ方がいいかもしれないが，注意して欲しいのは添え字の意味で，この文書では二つ目の添え字が応力の向きを表すように定義してある。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... 定義する基底ベクトルを表して ^12.14

この添え字の意味も，文献あるいは大学・学派によって逆なものも多いので注意する。特にnominal応力のように非対称（後述）なテンソルの場合には，その物理的な意味を考えるときやつり合い式を求めるときに特に注意が必要である。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... Piola-Kirchhoff応力について最もわかり難いところ ^12.15

著名な文献[25]の解説もわかり難い。文献によっては，初期配置の単位面に

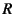が生じているような図があった記憶があるが，ますますわかり難い。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... どちらかと言えばnominal応力の方 ^12.16

多くの文献にある定義なら第1 Piola-Kirchhoff応力の方だが，そのような文献で第1 Piola-Kirchhoff応力をnominal応力とは呼ばないことから，この文書つまり文献[59]の定義の方が説得力がある・・・かな。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... stress'と訳される ^12.17

`engineering stress'や`conventional stress'という訳も使われるようだ。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...で回転している状態 ^12.18

これは文献[59]の著者Nemat-Nasser教授のアイデアであり，多くの文献にある数学的な考察に比べて第1著者にはとてもわかり易かったので，ここでも用いた。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...と定義 ^12.19

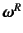理由は忘れてしまったが，随分前の若手（つまり第1著者が若かった頃ということ）の力学研究集会で，このTruesdellの応力速度を構成則に用いるのが一番よさそうだという話を，京都大学の西村直志先生にしていただいたような記憶がある。と思ったのだが，実はGreen-Naghdiの応力速度 （Cauchy応力のJaumann速度の $\fat{w}$ を $\fat{\omega}^R$ で置換した速度）をお奨めしておられるそうなので勘違いかもしれない。ただこのGreen-Naghdiの応力速度のupdated Lagrange的な速度はCauchy応力のJaumann速度になってしまう。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... 増分つり合い式を使う可能性 ^12.20

後述の増分Newton-Raphson法のように，応力を増分から求めてつり合いを考えるという方法もあるようだ。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...で大丈夫 ^12.21

次元としては 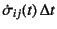$\dot{\sigma}_{ij}(t) \Delta t$ と記すべきであるが，上付きドットの量を増分と捉えて略記している。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...で ^12.22

内部エネルギ率 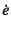$\dot{e}$ のうちの応力の仕事率の表現は，それぞれの応力テンソルに対して式(12.103)にまとめてある。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...の例に一致 ^12.23

例からも明らかなように実用的な構成則にはならない。Hookeの等方弾性テンソルを 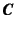$\fat{C}$ に用いた材料をSt.Venant-Kirchhoff材料と呼ぶ[12]らしい。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... 天才 ^12.24

秀才ではなく天才。アルゴンヌ国立研究所の故井口道生教授によると，Einsteinは実験・実測の観察をモデル化したのではなく，「こうだったらいいなぁ」と理論を作り上げるアプローチをとるらしく，誰にも真似はできないとのこと。我々凡人はやはり，物理的に意味のある量の観察から物理的な関係式にモデル化するのが精一杯だろう。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...保存的ではなくエネルギ散逸が避けられないということ ^12.25

任意の応力状態で式(12.137)が必ずしも積分可能ではないことから，載荷後除荷しても元には戻らない，あるいは変形を元に戻したときに残留応力が生じる。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...という組み合わせ ^12.26

特にnominal応力は非対称テンソルであるから，ここで用いる対称なひずみと線形関係で結び付けるのはおかしいが，例として1軸状態を対象とするので，それぞれの関係の特徴を比較するために用いている。実際，式(12.103)の応力の仕事率の表現は，nominal応力はLagrange的な速度勾配と関連付けることを示唆している。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...まずJaumannの応力速度で ^12.27

この例は体積変化が無いので，Cauchy応力のJaumann速度を用いた場合とKirchhoff応力のJaumann速度を用いた場合とは同じ結果になる。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... ズレあるいはすべり変形が連続的に分布・蓄積する ^12.28

転位が移動することによって結晶格子にズレが生じることから，移動する転位が通過した面上にあたかもすべり変形が残存したようにモデル化している。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...は非可逆的な変形 ^12.29

第1著者が学生のとき，電子顕微鏡の映像の中で転位線が同じところを行ったり来たりしているのを見たことがある。界面に達するまでは元に戻れるのかな。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... そこでは，空隙の発生と単結晶粒の剛体的な回転 ^12.30

村先生のimpotent eigenstrainがこれかな?呵呵。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... 単調載荷によって変化する降伏曲面を模式的に ^12.31

正確な図は文献[43]を。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... と呼んで ^A.1

降伏点とも呼ぶようだが，第1著者は嫌いなので，この文書では用いない。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... この欠陥はそれほど大きくない力（せん断力 ^A.2

単純に引張っても，内部に結晶の向きが違う単結晶がランダムに分布しているため，微視的にはせん断状態になる。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... 移動する。しかし，転位が単結晶の境界（界面）^A.3

鋼等のバルク材は多結晶材料で，内部には，それぞれがある一つの向きを持った単結晶が，不規則に多数分布している。その単結晶同士の境界は，必ずしも結晶格子構造のような強い結合をしているとは限らない。むしろ，結晶面の向きが異なることによる格子定数の見かけ上の差があることから，転位が最初から並んでいると考えるといい。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...だけ変位させた ^B.1

幾何学的境界条件が与えられた部分では零になるような許容場であるはずだが，ここでは厳密な扱いはしていない。後述の 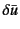$\delta\bar{u}$ の扱いも同様である。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... 広く知られている応用例は，内臓のエコー検査 ^G.1

第1著者が年1回の心エコー検査でreal timeで見ている動画は実は偽者なのだそうだ。人間の体内組成はあまりにも簡単なので，得られた信号を簡単に積分できて，心臓の弁が動いていたり血液がどちら向きに流れているかを，ほぼreal timeで表示できるのだそうだ。驚きである。第1著者が自分の大腸の内部を内視鏡で観察したときとはまた違う次元の驚きである。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...Truss-p.exe'を実行 ^H.1

Windows 7等でもし起動せずエラーになる場合には，`Truss-p.exe'のファイルアイコンを右クリックして「プロパティ」を出し，「互換性」のタブで「互換モードで実行する（Win XP）」をクリックして再実行する。それでも駄目な場合には，マルチメディア棟のXP端末等で実行する。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... パワーポイント ^H.2

パワーポイントの場合は，研究室のコンピュータに入っているプログラムのバージョンが古いので，自分のコンピュータを持参して発表するか，「Microsoft PowerPoint 97/2000/XP (xls)」として保存したファイルにすること。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... (ミウラ折り)\fakejchar ^H.3

British Origami Societyで`miura-ori'と名づけられたそうだ。正確な折り方と著作権についてはインターネット参照のこと。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... 非弾性ひずみ（塑性ひずみと同じように ^I.1

温度ひずみは最終状態の温度で唯一に値が決まるので，塑性ひずみのような流れ則には支配されない。したがって，全ひずみで弾性ひずみと加算すればいい。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.