�ŐV�ł𐳊m�ɓǂޏꍇ�ɂ� pdf �t�@�C�� ���ǂ����B����� web �����̂��߂̊ȈՋ��łł��B
���āC���͂Ƃ͕��̓����̒�R�͂ł���C����ƂЂ��݂̎ړx�Ƃ� �W�ł��̍ޗ��̒�R���܂�\�������L�q���邱�Ƃɂ��Ă������B ���͂͒P�Ȃ鐔�w�I�͊w�I�ȊT�O�ł���C�Ђ��݂̎ړx�� �����Ɋw�I�ȗʂł���B �e���̓e���\���Ԃɂ͖��m�Ȓ�`�̈Ⴂ�Ƃ��݂��̊W�����邩��C �\�����ɂ͂ǂ̉��̓e���\����p���Ă��\��Ȃ��B �������C�e���̓e���\���Ԃ̊W�ɂ͕ό`�̔���`�������܂܂�Ă��邱�Ƃɂ� ���ӂ͕K�v���B ����C�Ђ��݂̎ړx����������`�ł���B �����ŏI�I�ɂ͒P���ȍޗ������C�Ⴆ�Έ����莎���ō\������ ��߂�ȊO�ɂ͎肪�����B �Ƃ����̂��C��X�̐g�̉��ɂ���ޗ��̂قƂ�ǂ��傫�Ȕ�ώ��� �����܂�i�o���N�ށj�ł���C �K���������̔����I�ȃ��J�j�Y�������f�������čޗ��̋����I�Ȓ�R���� �\�����Ƃ��������ł���B
�ł��P�������Ȃ̂́C�����莎���̊O�͂��邢�͂���������O��
�����Ђ̒f�ʐςŊ�������������̉���![]() �ƁC
�L�тЂ��ݗႦ�Αΐ��Ђ���
�ƁC
�L�тЂ��ݗႦ�Αΐ��Ђ���![]() �Ƃ̊W����C
�\�������߂���@���낤�B
�ΐ��Ђ��݂�p���闝�R�́C�q�ϐ������ό`���x
�Ƃ̊W����C
�\�������߂���@���낤�B
�ΐ��Ђ��݂�p���闝�R�́C�q�ϐ������ό`���x![]() �������I��
�ΐ��Ђ��ݑ��x�ł��邱�Ƃ����邪�C
�L�т�2�{�Ək�݂̔����Ƃ������̓����l�ŕ\�����Ƃ�
�ł��邱�Ƃ������I�ȑf���������邩��ł���B
�܂��{�I�ȁu���`�e���́v���C���鉞��
�������I��
�ΐ��Ђ��ݑ��x�ł��邱�Ƃ����邪�C
�L�т�2�{�Ək�݂̔����Ƃ������̓����l�ŕ\�����Ƃ�
�ł��邱�Ƃ������I�ȑf���������邩��ł���B
�܂��{�I�ȁu���`�e���́v���C���鉞��
![]() ��
����Ђ��ݎړx
��
����Ђ��ݎړx
![]() ���C�萔�W����4�K�̃e���\��
���C�萔�W����4�K�̃e���\��![]() ��
�W�t��
��
�W�t��
�ƒ�`������ň����莎�����ʂ��V�~�����[�V�������C
����
![]() �̊W��
�ł��邾��
�̊W��
�ł��邾��![]() �ɑ��Đ��`�ł���ޗ����u���`�e���́v�ł����
�����邱�Ƃ��C�����I�ɂ͂悳�����Ɏv�����ǂ����낤�B
�܂�C�d�ƕό`�̎������ʂ̊W�ɂ����āC
���͂ƂЂ��݂̒�`�ɑ��݂���ό`��
����`���������Ō����悤�Ȍ�������̔���`���́C�ł��邾��
�����������������낤�B
���������ޗ�����`���́C
�萔�W����4�K�̃e���\��
�ɑ��Đ��`�ł���ޗ����u���`�e���́v�ł����
�����邱�Ƃ��C�����I�ɂ͂悳�����Ɏv�����ǂ����낤�B
�܂�C�d�ƕό`�̎������ʂ̊W�ɂ����āC
���͂ƂЂ��݂̒�`�ɑ��݂���ό`��
����`���������Ō����悤�Ȍ�������̔���`���́C�ł��邾��
�����������������낤�B
���������ޗ�����`���́C
�萔�W����4�K�̃e���\��
![]() ��
��
![]() (
(![]() , 2,
, 2, ![]() )��p���č\�����ɂЂ��݂̍��������܂ނ���
)��p���č\�����ɂЂ��݂̍��������܂ނ���
��C�ޗ��p�����[�^
![]() �̉��͂�Ђ��݂ւ̈ˑ���
�̉��͂�Ђ��݂ւ̈ˑ���
�ɂ���ĕ\������Ȃ���Ȃ�Ȃ��ƍl����ׂ����낤�B
������
![]() �͎�(12.22)�̂悤��
�͎�(12.22)�̂悤��
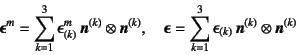
�Œ�`���ꂽ2�K�̃e���\���ł���B
![]() ��
��Ђ��݂ł���C
��
��Ђ��݂ł���C![]() �͎�����ł���B
�|��S����
�͎�����ł���B
�|��S����
![]() �͂��܂�K�v�ł͂Ȃ����낤���C
�R���N���[�g��n�Սޗ��ɂ�
�͂��܂�K�v�ł͂Ȃ����낤���C
�R���N���[�g��n�Սޗ��ɂ�
![]() �͕K�{�ɂȂ肻�����B
�͕K�{�ɂȂ肻�����B
�ȒP�ȗ�������Ă������B�ȉ��C�ȒP�̂��߂ɉ��͂̎�����ւ�1��
��R��Ԃɂ����āC���̓�������������Ƃ���Ђ��݂������Ă���Ƃ���B
�Ⴆ��Cauchy����![]() �ƐL�тЂ���
�ƐL�тЂ���![]() �i����ԍ��W��
�ϊ��������́j�Ƃ̊ԂɁC�萔�W��
�i����ԍ��W��
�ϊ��������́j�Ƃ̊ԂɁC�萔�W��![]() �����
�����
�̂悤�ȊW������ƒ�`��������ƁC�����
�Ƃ����d�ό`�W���Č��������Ƃɑ�������B![]() ��
��![]() ��
����2�厲�����̃X�g���b�`�ł���B
�܂�C��̎�(
��
����2�厲�����̃X�g���b�`�ł���B
�܂�C��̎�(![]() )���ޗ��̒�R�����Ƃ���ƁC
)���ޗ��̒�R�����Ƃ���ƁC![]() ��
��![]() �Ƃ̊Ԃ�
����`�W�ɂȂ炴��Ȃ����Ƃ������Ă���B
������̗�Ƃ��đ�2 Piola-Kirchhoff���͂Ƒΐ��Ђ��݂�Green�̂Ђ��݂�
�Ԃɓ��l��
�Ƃ̊Ԃ�
����`�W�ɂȂ炴��Ȃ����Ƃ������Ă���B
������̗�Ƃ��đ�2 Piola-Kirchhoff���͂Ƒΐ��Ђ��݂�Green�̂Ђ��݂�
�Ԃɓ��l��
�Ƃ������`�W������ƒ�`�����Ƃ���ƁC����͂��ꂼ��
�Ƃ����d�ό`�W���Č����悤�Ƃ������Ƃɑ�������B
�����![]() ��
��![]() �Ƃ̊Ԃ͔���`�W�ɂȂ炴��Ȃ��B
���̂悤�Ȕ���`���́C�ޗ������ł͂Ȃ��C���͂ƂЂ��݂̒�`��
���݂���w�I����`�������琶�������̂ł��邱�Ƃɂ͏\�����ӂ��K�v���B
�Ƃ̊Ԃ͔���`�W�ɂȂ炴��Ȃ��B
���̂悤�Ȕ���`���́C�ޗ������ł͂Ȃ��C���͂ƂЂ��݂̒�`��
���݂���w�I����`�������琶�������̂ł��邱�Ƃɂ͏\�����ӂ��K�v���B
�Z�o�@�ɂ��Ă͌�q���邪�C![]() % ���x�̂Ђ��݂͈̔͂�
���̂悤�Ȃ������̃��f���ɂ��d�ό`�W��
�������̂��}-12.13�ł���B
�ޗ�������\���\����������C�ǂ��炩�ƌ����C
���̂ɌЕt�����ꂽ���W�ŋL�q����Lagrange��@�̕��ނɊ܂܂��ړx��
�p���������悳�������B
�������C�}-12.13(a)�͂܂����k���ޗ��̏ꍇ�����C
����Lagrange�I�ȗ�̈�ł���
��2 Piola-Kirchhoff���͂�Green�Ђ��݂�p���������́C
��≺�ɓʂ̉d�ό`�W�ɂȂ��Ă���B
�܂������ł͍d�����C���k�ł͓����B
����͗Ⴆ�ΐg�߂ȍޗ��ł���u�����S���v�̋����Ƃ͂���Ă���悤�Ɋ�����B
�S���͔k���ޗ��Ȃ̂ŁC�}-12.13(b)�ɂ�
���̗���������B
��͂��2 Piola-Kirchhoff���͂�Green�Ђ��݂�p����������
���`����̂������r�I�傫����������B
�܂�C���͂ƂЂ��݂̒�`�Ɋ܂܂�����`���̉e�������̂��炢����Ƃ������Ƃ�
�F��������ŁC�\�������\�z����K�v������̂ł���B
�����C�Љ��Ս\���őΏۂƂ��Ă���ޗ��̂قƂ��ǂ�
��%�̕ό`���x���ʼn��Ă��܂��̂ŁC
���̂悤�ȍޗ��ɑ��ẮC�I�������ړx�̈Ⴂ���\�����ɋy�ڂ��e����
���̒��x���������ƍl���Ă�����Ă�������������Ȃ��B
% ���x�̂Ђ��݂͈̔͂�
���̂悤�Ȃ������̃��f���ɂ��d�ό`�W��
�������̂��}-12.13�ł���B
�ޗ�������\���\����������C�ǂ��炩�ƌ����C
���̂ɌЕt�����ꂽ���W�ŋL�q����Lagrange��@�̕��ނɊ܂܂��ړx��
�p���������悳�������B
�������C�}-12.13(a)�͂܂����k���ޗ��̏ꍇ�����C
����Lagrange�I�ȗ�̈�ł���
��2 Piola-Kirchhoff���͂�Green�Ђ��݂�p���������́C
��≺�ɓʂ̉d�ό`�W�ɂȂ��Ă���B
�܂������ł͍d�����C���k�ł͓����B
����͗Ⴆ�ΐg�߂ȍޗ��ł���u�����S���v�̋����Ƃ͂���Ă���悤�Ɋ�����B
�S���͔k���ޗ��Ȃ̂ŁC�}-12.13(b)�ɂ�
���̗���������B
��͂��2 Piola-Kirchhoff���͂�Green�Ђ��݂�p����������
���`����̂������r�I�傫����������B
�܂�C���͂ƂЂ��݂̒�`�Ɋ܂܂�����`���̉e�������̂��炢����Ƃ������Ƃ�
�F��������ŁC�\�������\�z����K�v������̂ł���B
�����C�Љ��Ս\���őΏۂƂ��Ă���ޗ��̂قƂ��ǂ�
��%�̕ό`���x���ʼn��Ă��܂��̂ŁC
���̂悤�ȍޗ��ɑ��ẮC�I�������ړx�̈Ⴂ���\�����ɋy�ڂ��e����
���̒��x���������ƍl���Ă�����Ă�������������Ȃ��B
���邢�́C�Y���̊T�O��O���ɒu����updated Lagrange�I�莮����
�\������\�����C
����K�ɒ�`���ꂽ����
![]() ��
�q�ϐ��������x��p���āC�q�ϐ������ό`���x�Ƃ̊Ԃ̊W��
�^����̂��]�܂������낤�B
�Ⴆ�Βe���Ȃ�
��
�q�ϐ��������x��p���āC�q�ϐ������ό`���x�Ƃ̊Ԃ̊W��
�^����̂��]�܂������낤�B
�Ⴆ�Βe���Ȃ�
�̂悤�ɒ�`���C���邢�͒e�Y���Ȃ�
�̂悤�ȊW���Œ�`����̂��]�܂����ƍl������B![]() ��
�ł��P���ɂ͒萔���B
�q�ϐ��������͑��x
��
�ł��P���ɂ͒萔���B
�q�ϐ��������͑��x
![]() �̑I���ɂ��ẮC
�������̗�����ƂŎ������C
���̂����̂�������p���Ē萔�W���̒e���̏ꍇ���C
�̑I���ɂ��ẮC
�������̗�����ƂŎ������C
���̂����̂�������p���Ē萔�W���̒e���̏ꍇ���C![]() % ���x��
�Ђ��݂͈̔͂Ő}-12.14�Ɏ������B
���̏ꍇ�͋t�ɁCupdated-Lagrange�I��Truesdell�̉��͑��x��p�������f����
���`���������ł���̂͋����[���B
�����Ƒ傫�ȕό`�ɑ���V�~�����[�V�����͌�q����B
% ���x��
�Ђ��݂͈̔͂Ő}-12.14�Ɏ������B
���̏ꍇ�͋t�ɁCupdated-Lagrange�I��Truesdell�̉��͑��x��p�������f����
���`���������ł���̂͋����[���B
�����Ƒ傫�ȕό`�ɑ���V�~�����[�V�����͌�q����B
��(3.47)����ʉ����C
���̂悤�ȂЂ��݃G�l���M���x��
![]() �����e�������e��
�ƌĂԁB
�����e�������e��
�ƌĂԁB
�����ɁC![]() ,
, ![]() �͕ό`�O��̖��x�ł���C
�E�ӂ͉��͂̎d����
�͕ό`�O��̖��x�ł���C
�E�ӂ͉��͂̎d����![]() ��12.22����B
���ꂪ��������ꍇ�ɂ�
��12.22����B
���ꂪ��������ꍇ�ɂ�
�Ƃ����\���W����������B
�����C
![]() ���萔�W����
���萔�W����![]() ��2���`���ɂȂ�Ƃ�
�l������C����͑O�߂���ю��߂̒萔�W��
��2���`���ɂȂ�Ƃ�
�l������C����͑O�߂���ю��߂̒萔�W��![]() ��
����
��
����
![]() �̗�Ɉ�v12.23����B
�������C���͈ˑ��̔C�ӂ̔���`�p�����[�^���܂ޖ��x���̌`��
���肵����ŁC�����ɂ�铯�������ςނ��Ƃł͂��邪�C
�����ɂ͂��܂蕨���͊������Ȃ��B
�܂��O�߂̂悤�ȉd�ό`�W�̔���`����L���Ă��邱�Ƃ����ӂ��Ȃ��Ƃ����Ȃ��B
�܂�C�����I�ȈӖ������܂薾�m�ł͂Ȃ�Green�̂Ђ��݂̕s�ϗʂ̂悤��
���̂�p���āC����ɂ��́u�|�e���V�����v�i��1���҂ɂ�
����s�\�j�ɑ����������`��
�Ђ��݃G�l���M���x��
�̗�Ɉ�v12.23����B
�������C���͈ˑ��̔C�ӂ̔���`�p�����[�^���܂ޖ��x���̌`��
���肵����ŁC�����ɂ�铯�������ςނ��Ƃł͂��邪�C
�����ɂ͂��܂蕨���͊������Ȃ��B
�܂��O�߂̂悤�ȉd�ό`�W�̔���`����L���Ă��邱�Ƃ����ӂ��Ȃ��Ƃ����Ȃ��B
�܂�C�����I�ȈӖ������܂薾�m�ł͂Ȃ�Green�̂Ђ��݂̕s�ϗʂ̂悤��
���̂�p���āC����ɂ��́u�|�e���V�����v�i��1���҂ɂ�
����s�\�j�ɑ����������`��
�Ђ��݃G�l���M���x��![]() ���`����̂́C
�V��12.24�ȊO�ɂ͍���Ȏd�����낤�B
��͂蕨���I�Ȋώ@�ƍl�@���璼�ډ��͂ƂЂ��݁C���邢�͉��͑��x�ƂЂ��ݑ��x��
���ѕt����悤�ȃA�v���[�`�ō\�����f�����`��������킩��Ղ��B
�������C��-E.2�Œ莮������Bernoulli-Euler����
�ꍇ�́C��2 Piola-Kirchhoff���͂�Green�Ђ��݂̂��ꂼ�������������p����
���`����̂́C
�V��12.24�ȊO�ɂ͍���Ȏd�����낤�B
��͂蕨���I�Ȋώ@�ƍl�@���璼�ډ��͂ƂЂ��݁C���邢�͉��͑��x�ƂЂ��ݑ��x��
���ѕt����悤�ȃA�v���[�`�ō\�����f�����`��������킩��Ղ��B
�������C��-E.2�Œ莮������Bernoulli-Euler����
�ꍇ�́C��2 Piola-Kirchhoff���͂�Green�Ђ��݂̂��ꂼ�������������p����
�Ƃ����G�l���M���x������`�ł��C���͂Ђ��݊W��
�Ƃ����������I�ȗʓ��m�ŕ\�����Ƃ��ł���B ����ɂ���Ĕ��ɔ��������_���\�z����Ă���B
�Ƃ���ŁC�Ђ��݃G�l���M���x���̑�\��Ƃ��ẮC
�悭�S���̂悤�ȍޗ��̃��f���Ƃ��ėp������
�k���ޗ���Mooney-Rivlin���f����
�Ƃ�����������B�����ɁC![]() ��
��
![]() ��
�ޗ��p�����[�^�ł���C
��
�ޗ��p�����[�^�ł���C![]() ,
, ![]() �͓K�ɑI�ό`��
��1, 2�s�ϗʂł���B�Ⴆ��
�͓K�ɑI�ό`��
��1, 2�s�ϗʂł���B�Ⴆ��![]() �̎�l��p�����
�̎�l��p�����
�ł���B���Ƃň�Cnominal���͂�p�����ꍇ�̗�������B
�Ƃ�����������������̂Ƃ��Ē�`�����B![]() ��
��ʂɂ͉��͂̊��ł���B
�������`���e���̂̏ꍇ�C���͂Ɉˑ����Ȃ����̂�
��(3.50b)��
��
��ʂɂ͉��͂̊��ł���B
�������`���e���̂̏ꍇ�C���͂Ɉˑ����Ȃ����̂�
��(3.50b)��![]() �ŕ\�����B
���ӂ��Ȃ��Ƃ����Ȃ��̂́C���̒e���\�����f�����ۑ��I�ł͂Ȃ��G�l���M�U�킪�������Ȃ��Ƃ�������12.25�ł���B
��ʂɂ�
�ŕ\�����B
���ӂ��Ȃ��Ƃ����Ȃ��̂́C���̒e���\�����f�����ۑ��I�ł͂Ȃ��G�l���M�U�킪�������Ȃ��Ƃ�������12.25�ł���B
��ʂɂ�
�̂悤�ɗ^�����![]() ����
����![]() �͉��͂̕s�ϗʂ̊���
�^������W��[119]�ł���B
�͉��͂̕s�ϗʂ̊���
�^������W��[119]�ł���B
�K�ȉ��̓e���\��
![]() ��
����ɑΉ�����Ђ��݃e���\��
��
����ɑΉ�����Ђ��݃e���\��
![]() ��
���钼���ٕ�����L����ޗ��萔�Ō��т���
��
���钼���ٕ�����L����ޗ��萔�Ō��т���
�̂悤�ȃ��f�����������l���Ă݂悤�B
�������C�\�������l����Ƃ��́C�ޗ��������ʂ����Ȃ����̎��̂悤��
���f�����\�z���邱�ƂɂȂ�̂����C�����ł́C�����㎮�̂悤��
�\��������������ޗ����������Ƃ��ɁC�L���ό`�̘g�g�̒���
�ǂ̂悤�Ȉ����莎�����ʂɑ�������̂��������B
�܂�����
![]() �̌��Ƃ��ẮC��2
Piola-Kirchhoff����
�̌��Ƃ��ẮC��2
Piola-Kirchhoff����![]() ��Kirchhoff����
��Kirchhoff����![]() ��Cauchy����
��Cauchy����![]() �C����ɏ����ςł͂��邪nominal����
�C����ɏ����ςł͂��邪nominal����![]() ���g���Ă݂�B
�Ή�����Ђ���
���g���Ă݂�B
�Ή�����Ђ���
![]() �ɂ́CGreen�̂Ђ���
�ɂ́CGreen�̂Ђ���![]() ��
�L���
��
�L�тЂ���![]() �ɑΐ��Ђ���
�ɑΐ��Ђ���![]() ���l���Ă݂悤�B
���͂̎d�����̎�(12.103)�ɂ���g�ݍ��킹
���l���Ă݂悤�B
���͂̎d�����̎�(12.103)�ɂ���g�ݍ��킹
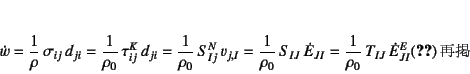
����̎����ł́C��2 Piola-Kirchhoff���͂�Green�̂Ђ��݂ƁC �܂�Kirchhoff���͂�Cauchy���͂͑ΐ��Ђ��݂ƊW�t���邱�Ƃ� �������Ă���̂ŁC�����ł�
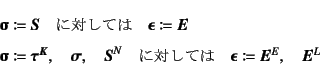
�Ƃ����g�ݍ��킹12.26�Œ��ׂĂ������B
�ł��P���ȃ��f���́C�O�߂̂Ђ��݃G�l���M���x��![]() ��
�Ђ��ݎړx��2���`���ɂȂ��Ă�����̂��낤����C
�ȒP�̂��߂ɉ~�f�ʖ_�̈����莎����ΏۂƂ��Ē���3��������
��l���́E�L�я�Ԃ��C���[�W����
��
�Ђ��ݎړx��2���`���ɂȂ��Ă�����̂��낤����C
�ȒP�̂��߂ɉ~�f�ʖ_�̈����莎����ΏۂƂ��Ē���3��������
��l���́E�L�я�Ԃ��C���[�W����
�Ƃ���B�����āC![]() �����̃��[�h�Z���̓ǂ݂������Ђ�
�ό`�O�̒f�ʐςŊ��������̉��͂�
�����̃��[�h�Z���̓ǂ݂������Ђ�
�ό`�O�̒f�ʐςŊ��������̉��͂�![]() �ŁC
���������̐L�т�
�ŁC
���������̐L�т�
![]() �������Ƃ��悤�B
���͂ƕό`�̏�Ԃ́C
�㎮(12.140)��
�������Ƃ��悤�B
���͂ƕό`�̏�Ԃ́C
�㎮(12.140)��
![]() ,
,
![]() ,
,
![]() ,
,
![]() �Ƃ�������B����������
�Ƃ�������B����������
�ƂȂ�B�e���͂́C���͂̕����I�ȈӖ������������Ƃ���
�p�������̎�(12.105)
(12.106) (12.107)
(12.108)�ŁC���̂̉�]![]() ���ɂ����������
���ɂ����������
�ƂȂ�B�Ђ��݂́CGreen�̂Ђ��݂�p����ꍇ�͎�(12.23)����
�ƂȂ�C�L�тЂ��݂̏ꍇ�͎�(12.44)����
�ΐ��Ђ��݂̏ꍇ����(12.44)����
�ƂȂ�B
�����p���ĉd�ƕό`�̊W��}-12.15��
���������C�L�тЂ��݂�
�����ɂƂ��ĕ\�������̂��}-12.15(a)�ŁC
�ΐ��Ђ��݂������ɂƂ����̂��}-12.15(b)�ł���B
�������C�ȒP�̂���
![]() �i����
�ό`���_�ɂ�����Hooke�̖@����Poisson�䂪
�i����
�ό`���_�ɂ�����Hooke�̖@����Poisson�䂪![]() ��
��������j�Ƃ����B
��Ԃ�������nominal���͂�p�������`�W�̍ޗ����f���̏ꍇ�ɂ́C
�d�ƕό`�̊W�͐��`�ɂȂ邪�C����ȍޗ��͑������݂��Ȃ����낤�B
����ȊO�́C���͂Ђ��݊W�͒萔�W���ŊW�t�����Ă���ɂ�
������炸�C���ꂼ��̉��͂�Ђ��݂̗L���ό`���_�ɂ������`��
�Ⴂ�ɂ���āC�d�ƕό`�̊W�͔���`�ɂȂ��Ă���B
�����đ�2 Piola-Kirchhoff���͂�
�p�����ꍇ�ƁCCauchy���͂����Kirchhoff���͂̏ꍇ�Ƃ́C
��ό`���ɋt�̉��������������Ă���B�܂�C
��2 Piola-Kirchhoff���͂�Green�̂Ђ��݂�p�������`�W�̍ޗ��́C
������ɂ�č��ɂȂ�C���k�������قǏ_�炩���Ȃ邱�Ƃ�
�����Ă���B�����葤�̉����̓S���̂悤�Ȕk�ޗ��Ōo������̂�
�����悤�ɂ͊����邪�C
���k����قǏ_�炩���Ȃ�ޗ��͂��܂�G�������Ƃ��Ȃ��悤�Ɋ�����B
����́CSt.Venant-Kirchhoff�ޗ�
�ƌĂ�[12]�C
���p�I�ł͂Ȃ��Ƃ���Ă���B
�������C�����ό`�͈̔͂ł́C�ǂ�ȍ\������p���Ă���ʂ͕t���Ȃ��B
��
��������j�Ƃ����B
��Ԃ�������nominal���͂�p�������`�W�̍ޗ����f���̏ꍇ�ɂ́C
�d�ƕό`�̊W�͐��`�ɂȂ邪�C����ȍޗ��͑������݂��Ȃ����낤�B
����ȊO�́C���͂Ђ��݊W�͒萔�W���ŊW�t�����Ă���ɂ�
������炸�C���ꂼ��̉��͂�Ђ��݂̗L���ό`���_�ɂ������`��
�Ⴂ�ɂ���āC�d�ƕό`�̊W�͔���`�ɂȂ��Ă���B
�����đ�2 Piola-Kirchhoff���͂�
�p�����ꍇ�ƁCCauchy���͂����Kirchhoff���͂̏ꍇ�Ƃ́C
��ό`���ɋt�̉��������������Ă���B�܂�C
��2 Piola-Kirchhoff���͂�Green�̂Ђ��݂�p�������`�W�̍ޗ��́C
������ɂ�č��ɂȂ�C���k�������قǏ_�炩���Ȃ邱�Ƃ�
�����Ă���B�����葤�̉����̓S���̂悤�Ȕk�ޗ��Ōo������̂�
�����悤�ɂ͊����邪�C
���k����قǏ_�炩���Ȃ�ޗ��͂��܂�G�������Ƃ��Ȃ��悤�Ɋ�����B
����́CSt.Venant-Kirchhoff�ޗ�
�ƌĂ�[12]�C
���p�I�ł͂Ȃ��Ƃ���Ă���B
�������C�����ό`�͈̔͂ł́C�ǂ�ȍ\������p���Ă���ʂ͕t���Ȃ��B
�}-12.16�ɂ́CCauchy���͂�Kirchhoff���͂�
���`�W���`�����e���̂̏ꍇ�̌��ʂ��������o�����B
���̏ꍇ���C��q�̑�2 Piola-Kirchhoff���͂�p�����ޗ��Ƃ͋t�ɁC
������قǏ_�炩���Ȃ�C���k����ƍ��ɂȂ��Ă���B
���k���́C��͂�S�����Ōo�����鋓���Ɠ����悤�Ɋ�����B
������ɂ��Ă��C���̂悤�Ȓ萔�W����p�������`�W�ŗ^������ޗ��́C
���ېg�̉��ɂ͖����悤�ȋC�����邪�C�ǂ����낤�B
�܁C�����Ƃ��C�e���Ђ��݂�����![]() %�ɒB���邱�Ƃ͖������낤����C
����قNjC�ɂ���K�v���Ȃ���������Ȃ��B
%�ɒB���邱�Ƃ͖������낤����C
����قNjC�ɂ���K�v���Ȃ���������Ȃ��B
�ł́C�S���̂悤�Ȕk���ޗ��̗�����Z���Ă݂悤�B
���̂悤�ȏꍇ�ɂ�
![]() �Ƃ���
�Ƃ���
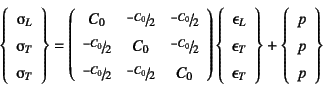
�Ƃ�������B���͂���́C�����ό`���_�ɂ�����
��(3.40) (3.41)��Hooke�̖@����
�Ƃ݂Ȃ������f���ɑ������邪�C�����Poisson�䂪![]() �ł͂Ȃ��C
��������̋Ɍ���
�ł͂Ȃ��C
��������̋Ɍ���![]() (
(
![]() )�ɑ�������B
�����ψʗ��_�͈̔͂ł́C�k����
)�ɑ�������B
�����ψʗ��_�͈̔͂ł́C�k����
![]() �ŋߎ������
���邽�߁C
�ŋߎ������
���邽�߁C![]() �̍ޗ��Ŕk���ޗ������f�����ł��邪�C
�L���ψʗ��_�͈̔͂̔k����
�̍ޗ��Ŕk���ޗ������f�����ł��邪�C
�L���ψʗ��_�͈̔͂̔k����
![]() �Ȃ̂ŁC
�㎮�̂悤�ȊW�ɂ��Ă݂��B
�������C������
�Ȃ̂ŁC
�㎮�̂悤�ȊW�ɂ��Ă݂��B
�������C������![]() �͕��ω��́i���̐Ð����j�ł���B
�܂��k���ŁC�����ł�1����ԂȂ̂�
�͕��ω��́i���̐Ð����j�ł���B
�܂��k���ŁC�����ł�1����ԂȂ̂�
�̏�������C![]() ��
��![]() �ŕ\�����Ƃ��ł���B
�ŕ\�����Ƃ��ł���B
![]() �̏ꍇ�ɂ�
�̏ꍇ�ɂ�
![]() ��I�����C
�k���̏ꍇ�ɂ�Cauchy���͂�Kirchhoff���͂�
��v����̂ŁC
��I�����C
�k���̏ꍇ�ɂ�Cauchy���͂�Kirchhoff���͂�
��v����̂ŁC
![]() ��
����
��
����
![]() ��
��![]() ��I�������B
���ʓI��
��I�������B
���ʓI��
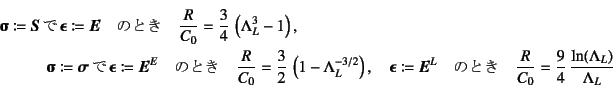
�ƂȂ�B�����}�������̂��}-12.17�ł���B �S�̓I�ȓ����̈Ⴂ�͈��k���ޗ��̏ꍇ�Ɠ��l�����C �d�̃��x����3�{���炢�ɂ܂ŏオ���Ă���B
�k���ޗ��̏ꍇ�́C
�Ђ��݃G�l���M���x���̗�Ƃ��ċ�����
��(12.135)��Mooney-Rivlin���f��
���L���ł���B�������ʉ���
�Ƃ��悤�B������![]() ,
, ![]() �͕ό`�e���\��
�͕ό`�e���\��![]() �̑�1, 2�s�ϗʂƂ��C
�̑�1, 2�s�ϗʂƂ��C
�Ƃ��Ă������B������nominal���͂�
�ƊW�t���邱�Ƃ��ł���Ƃ���B������![]() �͕��̐Ð����ł���B
�k���ޗ��Ȃ̂ŁC���ꂩ��Cauchy���͂�
�͕��̐Ð����ł���B
�k���ޗ��Ȃ̂ŁC���ꂩ��Cauchy���͂�
| (12.144) |
�ƕ\�����Ƃ��ł���B
�����ŏ�̗�Ɠ����悤��1���ډׂ�z�肵��![]() ����������
����������![]() ,
,
![]() �����߂�ƁC�ŏI�I��
�����߂�ƁC�ŏI�I��
�Ƃ����W��B
��̗��![]() �ɂ�������z�i�����j����v�����悤�Ƃ����
�ɂ�������z�i�����j����v�����悤�Ƃ����
�ƕ��ɂȂ��Ă��܂����C���̌��ʂ��}-12.17��
���ׂ��B�}��`MR![]() '�Ƃ���̂����̌��ʂł���B
'�Ƃ���̂����̌��ʂł���B![]() ������
�Ȃ��Ă��邪�C����͔����ό`���_�ɂ�����Poisson���
������
�Ȃ��Ă��邪�C����͔����ό`���_�ɂ�����Poisson���
![]() �Ƃ���
�ꍇ�ɑ������C���̍ޗ��͈���ł͂�����̂̕����ޗ��̂悤�ȓ���ȍޗ�������
�������Ă��܂��̂ŁC���l�����̂܂ܐ��C�܂�
�Ƃ���
�ꍇ�ɑ������C���̍ޗ��͈���ł͂�����̂̕����ޗ��̂悤�ȓ���ȍޗ�������
�������Ă��܂��̂ŁC���l�����̂܂ܐ��C�܂�
�Ƃ������̂��Q�l�Ƃ���`MR![]() '�Ƃ��Ď����Ă������B
���̏ꍇ���C��2 Piola-Kirchhoff���͂�p�����ꍇ�̋�������������
��������Ă���BMooney-Rivlin���f���͂��Ȃ����`����
�����\�����Ɍ����邪�C�d�ό`�W�͂قڐ��`�ɂȂ�̂͋����[���B
�Ȃ��CCauchy���͂�p�����ꍇ�̌��ʂ����Ƃ̔�r��
�ʓr�}-12.18�Ɏ����Ă������B
'�Ƃ��Ď����Ă������B
���̏ꍇ���C��2 Piola-Kirchhoff���͂�p�����ꍇ�̋�������������
��������Ă���BMooney-Rivlin���f���͂��Ȃ����`����
�����\�����Ɍ����邪�C�d�ό`�W�͂قڐ��`�ɂȂ�̂͋����[���B
�Ȃ��CCauchy���͂�p�����ꍇ�̌��ʂ����Ƃ̔�r��
�ʓr�}-12.18�Ɏ����Ă������B
�܂��C����K�ɒ�`���ꂽ�q�ϐ�������
���x����
![]() ��p���āC
�q�ϐ������ό`���x�Ƃ̊Ԃ�
���钼���ٕ�����L����ޗ��萔�Ō��т���
��p���āC
�q�ϐ������ό`���x�Ƃ̊Ԃ�
���钼���ٕ�����L����ޗ��萔�Ō��т���
| (12.145) |
�̂悤�ȊW���ŁC�\�������`���邱�Ƃ��ł���B
�ł��L���p�����Ă���̂́CCauchy���͂�Jaumann���x�ƕό`���x��
�e���W���ŊW�t���郂�f�����낤�B�܂�
�ƂȂ�B��������e��
�̈��ŁC���̃��f�����ۑ��I�ł͂Ȃ��G�l���M�U�킪�������Ȃ��Ƃ������Ƃɂ͒��ӂ���B
�ēx�C3�������ւ̍ډ�Ԃ�Ώۂɂ���X�s���͂��ׂė�Ȃ̂ŁC
�㎮��
�ƂȂ�B�E�ӂ�![]() �͎�(12.65)�Œ�`����
�ΐ��Ђ��ݑ��x�ł���B�P���ȍډ�ԂȂ̂�
�͎�(12.65)�Œ�`����
�ΐ��Ђ��ݑ��x�ł���B�P���ȍډ�ԂȂ̂�
�ƂȂ�B������![]() �͒P�ʍs��ł���B
���������āC��(12.131)��Cauchy���͂̍X�V�K�����l������ƁC
�㎮(12.147)�͐ϕ��ł��āC����
�͒P�ʍs��ł���B
���������āC��(12.131)��Cauchy���͂̍X�V�K�����l������ƁC
�㎮(12.147)�͐ϕ��ł��āC����
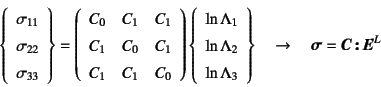
�̂悤�ɁCCauchy���͂Ƒΐ��Ђ��݂���`�W�Ō��ѕt�����O�߂� ���f���̈�Ɉ�v����B���������āC�����莎���̌��ʂ��C �O�߂̑Ή�����}�̂悤�ɂȂ�B
���邢�͎�(12.134)�����e��
�̃��f������C![]() �����m�ɒ�`�ł���ꍇ�ɂ͂������������
�����m�ɒ�`�ł���ꍇ�ɂ͂������������
�Ƃ��������W����������B
��ό`�����e����C���ɎЉ��Ս\���ɊW�����ޗ��̏ꍇ�ɂ́C
�ޗ��̐^�̏�����Ԃ��`���邱�Ƃ͍���ł���B
���������Ă���ό`��Ԃ��邢�͉��͏�Ԃ����̏�����ԂƂ���̂����C
���ǂ͊e��Ԃɂ����鑝���W�i���ꂩ��ǂ��Ȃ낤�Ƃ���̂��j��
�\�������`����������������ƍl������B
�܂�ő̂̏ꍇ��updated Lagrange�I�ȍ\�������`����̂��]�܂����B
�����ŏ㎮��updated Lagrange�I�ȋɌ����Ƃ�C
��(12.118) (12.120) (12.121)��
�p����CTruesdell���͑��x�ƕό`���x�̊Ԃ�
�Ƃ����\�������C���e���Ɠ����ȑ����\�����Ƃ��Đ�������B
�ł���{�I�ȃ��f���Ƃ��āC���̒e���W��
![]() ��
�萔�W����
��
�萔�W����![]() �ōĒ�`����
�ōĒ�`����
�ƊW�t�����\�������������邾�낤�B
���邢�́CCauchy���͂ł͂Ȃ��C
��(12.115)��Kirchhoff���͂�Jaumann���x�ƕό`���x�̊Ԃ�
�Ƃ������`�W������Ƃ��郂�f�����\���B
��(12.149)�̏ꍇ�ƁC
��(12.150)�̏ꍇ��2�҂̗�������āCCauchy���͂�Jaumann���x��
�p�����ꍇ�Ɣ�r���Ă������B
�������
�ƕ\�����Ƃ��ł���̂Őϕ��ł�
�Ə������Ƃ��ł���B������
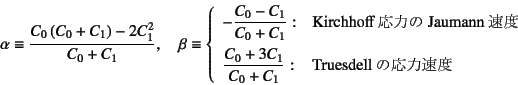
�ƒ�`�����B
�ȏ�̎O�̃��f����
![]() �Ƃ����ꍇ��
���ʂ��C2�{�̎�����1�{�̈�_�����Ő}-12.19�Ɏ������B
������Truesdell�̉��͑��x�̏ꍇ�ɂ�
�Ƃ����ꍇ��
���ʂ��C2�{�̎�����1�{�̈�_�����Ő}-12.19�Ɏ������B
������Truesdell�̉��͑��x�̏ꍇ�ɂ�
![]() ,
, ![]() ��
�ꍇ�����ׂĔj���ŕ`�������C
����͂��ꂼ������ό`���_��Poisson�䂪
��
�ꍇ�����ׂĔj���ŕ`�������C
����͂��ꂼ������ό`���_��Poisson�䂪![]() , 0.4�ɑ�������B
��͂艞�͑��x�̑I���̈Ⴂ�ɂ���āC
�����莎���̌��ʂɂ͑傫�ȍ�������Ă���B
�Ƃ���ŁCTruesdell�̉��͑��x��p�����ꍇ�̌��ʂ́C�c����
���̓��x���≡���̕ό`�ɂ��܂�ˑ������C���̌��z���قړ����ɂȂ��Ă���B
�Ⴆ�|���̌��������ޗ���Ώۂɂ���ƁC�قƂ�ǂ̒e���ό`������
�����i�q���̂��̘̂c�݂ł��낤���C����͉��̓��x�������łȂ��C
�]�ʂ̈ړ��ɂ�鋐���I�Ȕ�t�ό`�̃��x���Ɉˑ����Ȃ����̓�����
�l���Ă悳�������B
���������l�@�Ɋ�Â��C���������ޗ��̒e�������ɂ�Truesdell�̉��͑��x��
�p����̂�����������������Ȃ��Ǝv���C���̗�ł�3��ނ̍ޗ��p�����[�^��
�}�����Ă݂��B
, 0.4�ɑ�������B
��͂艞�͑��x�̑I���̈Ⴂ�ɂ���āC
�����莎���̌��ʂɂ͑傫�ȍ�������Ă���B
�Ƃ���ŁCTruesdell�̉��͑��x��p�����ꍇ�̌��ʂ́C�c����
���̓��x���≡���̕ό`�ɂ��܂�ˑ������C���̌��z���قړ����ɂȂ��Ă���B
�Ⴆ�|���̌��������ޗ���Ώۂɂ���ƁC�قƂ�ǂ̒e���ό`������
�����i�q���̂��̘̂c�݂ł��낤���C����͉��̓��x�������łȂ��C
�]�ʂ̈ړ��ɂ�鋐���I�Ȕ�t�ό`�̃��x���Ɉˑ����Ȃ����̓�����
�l���Ă悳�������B
���������l�@�Ɋ�Â��C���������ޗ��̒e�������ɂ�Truesdell�̉��͑��x��
�p����̂�����������������Ȃ��Ǝv���C���̗�ł�3��ނ̍ޗ��p�����[�^��
�}�����Ă݂��B
�k���ޗ��̑��x�^�\�����̏ꍇ�́C
�k���̏�������(12.60)�ŗ^������̂�
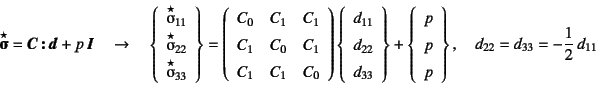
�̂悤�ȊW�Ń��f�����ł���B1����Ԃ�
�ΏۂƂ���̂ŁC
![]() ����
����![]() ���������āC
�O�߂̏ꍇ�Ɠ��l�̉��Z���o��
���������āC
�O�߂̏ꍇ�Ɠ��l�̉��Z���o��
![]() ��
���߂�ƁCTruesdell�̉��͑��x�̏ꍇ��
��
���߂�ƁCTruesdell�̉��͑��x�̏ꍇ��
�ƂȂ�CCauchy���͂�Jaumann���x�̏ꍇ��
�̂悤�ɐϕ��ł��邪�C
��҂͑O�߂̌��ʂƈ�v����B���Ȃ݂�
![]() �ł���B�}-12.20�ɂ́C
�O�߂Ɠ��l
�ł���B�}-12.20�ɂ́C
�O�߂Ɠ��l
![]() �ɂ���
�ꍇ�iPoisson��
�ɂ���
�ꍇ�iPoisson��![]() �����j�ƁC
�k�S�����̂̂悤�ɔ����ό`���_�ɂ�����
��(3.40) (3.41)��Hooke�̖@���ŁC
����f�������L�q����Ђ��݂ɂ͕��Ђ��݂ł͂Ȃ��S�Ђ��݂�p����
�����j�ƁC
�k�S�����̂̂悤�ɔ����ό`���_�ɂ�����
��(3.40) (3.41)��Hooke�̖@���ŁC
����f�������L�q����Ђ��݂ɂ͕��Ђ��݂ł͂Ȃ��S�Ђ��݂�p����
�Ƃ݂Ȃ����ꍇ�i![]() �����j�C
�܂�
�����j�C
�܂�
![]() �̏ꍇ�̌��ʂ��������B
������Truesdell�̉��͑��x��p�����ꍇ�ŁC�j����Cauchy���͂�Jaumann���x��
�ꍇ�ł���B
�X���Ƃ��ẮC���k���ޗ����f���̏ꍇ�Ƃقړ��l�ł���B
���̂������̗�Ŗ��炩�Ȃ悤�ɁC
�ł��P���Ȓ萔�W���̐��`�W�ō\�������`���Ă��C
���͂≞�͑��x����тЂ��݂̒�`�ɑ��݂������`���ɂ���āC
�d�ό`�W�͐��`����傫������邱�Ƃɂ͏\�����ӂ���K�v������B
�ޗ������Ɍ�������`���̂����C�ǂꂪ���̒�`�̔���`���ɂ����̂ŁC
�ǂꂪ�ޗ����̂��̂̔���`���Ȃ̂��C������Ƌ�ʂ���K�v������B
�ƂĂ�����Ƃ͎v�����B
�̏ꍇ�̌��ʂ��������B
������Truesdell�̉��͑��x��p�����ꍇ�ŁC�j����Cauchy���͂�Jaumann���x��
�ꍇ�ł���B
�X���Ƃ��ẮC���k���ޗ����f���̏ꍇ�Ƃقړ��l�ł���B
���̂������̗�Ŗ��炩�Ȃ悤�ɁC
�ł��P���Ȓ萔�W���̐��`�W�ō\�������`���Ă��C
���͂≞�͑��x����тЂ��݂̒�`�ɑ��݂������`���ɂ���āC
�d�ό`�W�͐��`����傫������邱�Ƃɂ͏\�����ӂ���K�v������B
�ޗ������Ɍ�������`���̂����C�ǂꂪ���̒�`�̔���`���ɂ����̂ŁC
�ǂꂪ�ޗ����̂��̂̔���`���Ȃ̂��C������Ƌ�ʂ���K�v������B
�ƂĂ�����Ƃ͎v�����B
���ɁCCauchy���͂�Jaumann���x��
�L���ȓ���[49]�ɂ���Truesdell�̉��͑��x��
�p�����ꍇ�Ɣ�ׂĂ������B�}-12.21��
�C���Z�b�g�Ɏ������悤�ɁC�����ƕ���ۂ����܂��ɂ���![]() �����ɂ���f�ό`
�����ɂ���f�ό`![]() ��^����B
���̏ꍇ�̕ψʐ�����
��^����B
���̏ꍇ�̕ψʐ�����
![]() �����Ȃ̂�
�����Ȃ̂�
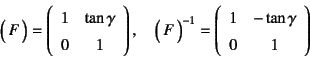
�ƂȂ�B�ȒP�̂��߂�![]() �̕����݂̂������B
�����ƕ���ێ����Ă���̂ő̐ϕω��͖���
�̕����݂̂������B
�����ƕ���ێ����Ă���̂ő̐ϕω��͖���![]() �̂܂܂ł���B
���ꂩ��
�̂܂܂ł���B
���ꂩ��
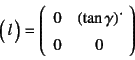
�ƂȂ�C�ό`���x�ƃX�s����
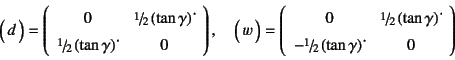
�ƂȂ�B
���[�h�Z�����ő���ł���ό`�O�̒P�ʖʐϓ������
�O�͎͂�(12.80)��nominal���͂�
��`��������̂ŁC���̕ό`�̏ꍇ��
�Ƃ����W�ɂȂ�B
�ʔ������Ƃɓ�����O�����C���̊W�͎����I�Ƀ��[�����g��
�荇��
![]() ��������B
��������B
�܂�Jaumann�̉��͑��x��12.27�\�������`����ꍇ���l���悤�B ��(12.114)�̒�`����C���̕ό`�̏ꍇ��
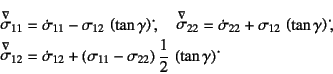
�ƂȂ�B���ꂪ![]() �Ƃ̊ԂɁC
�����ٕ�����L����萔�W���̐��`�W�ɂ���e���̂��Ƃ��C
�ό`���x��
�Ƃ̊ԂɁC
�����ٕ�����L����萔�W���̐��`�W�ɂ���e���̂��Ƃ��C
�ό`���x��![]() �݂̂����ł��邱�Ƃ���
�݂̂����ł��邱�Ƃ���
���������邱�ƂɂȂ�B![]() ������f�ڐ��W����Voigt�萔�ŁC
�����ό`���_��
������f�ڐ��W����Voigt�萔�ŁC
�����ό`���_��![]() �ɑ�������B
���ꂩ��
�ɑ�������B
���ꂩ��
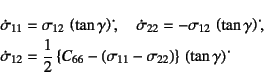
�ƂȂ�̂ŁC�܂�
�Ƃ����W��
�Ƃ����W�����߂���B��҂͐ϕ��ł���
�i�ȉ~��̋O�Ղ�`���j�܂�
�ƒu���Ă����̂ŁC�������̉��͑��x
![]() �̎�
�̎�
�ɑ������
��B���������āC�ŏI�I�Ɋe���͐�����
�Ƌ��߂��C�������(![]() )�ɑ�����ĊO�͂����߂��
)�ɑ�����ĊO�͂����߂��
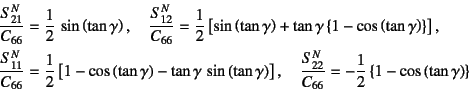
�ƂȂ�B
���̍ŏ��̎���}-12.21�Ɏ������B![]() ��
��57.5�x��
��
��57.5�x��![]() �̍ő�l�ɒB���C���Ƃ�
�̍ő�l�ɒB���C���Ƃ�
![]() ��
�����Ė����ɒׂ�čs��sine�Ȑ��ɂȂ�B
����͒����I�ɂ����Ȃ��ȋ����ɂȂ��Ă��܂��Ă���B
�܂������S����ׂ��Ă݂Ċ�����悤�ɁC
��
�����Ė����ɒׂ�čs��sine�Ȑ��ɂȂ�B
����͒����I�ɂ����Ȃ��ȋ����ɂȂ��Ă��܂��Ă���B
�܂������S����ׂ��Ă݂Ċ�����悤�ɁC![]() ������ɂȂ�Ȃ�
���ʂ͐������悤�ɂ������邩������Ȃ����C
�������ɍs�����ꍇ�ɂ́C���ϓI�ɂ͂������ɂȂ�̂ł͂Ȃ����낤���B
������ɂ��Ă��CJaumann�̉��͑��x�̓K�p�͈͂́C�p�x
������ɂȂ�Ȃ�
���ʂ͐������悤�ɂ������邩������Ȃ����C
�������ɍs�����ꍇ�ɂ́C���ϓI�ɂ͂������ɂȂ�̂ł͂Ȃ����낤���B
������ɂ��Ă��CJaumann�̉��͑��x�̓K�p�͈͂́C�p�x![]() ��
��������45�x���炢�܂ł��낤�B
��
��������45�x���炢�܂ł��낤�B
���ɁCTruesdell�̉��͑��x�ō\�������`����ꍇ���l���悤�B
�����őΏۂƂ��Ă���ό`��Ԃ͑̐ϕω��������̂ŁC
�\������Oldroyd�̉��͑��x��p�����ꍇ���������ʂɂȂ�B
��(12.121)�̒�`����C���̕ό`�̏ꍇ��
�ƂȂ�B���ꂪ![]() �Ƃ̊ԂɁC
�����ٕ�����L����萔�W���̐��`�W�ɂ���e���̂��Ƃ���B
���ǁC���ꂩ��
�Ƃ̊ԂɁC
�����ٕ�����L����萔�W���̐��`�W�ɂ���e���̂��Ƃ���B
���ǁC���ꂩ��
�ƂȂ�B����͗e�Ղɐϕ��ł��āC�ŏI�I�Ɋe���͐�����
�Ƌ��߂��B�������(![]() )�ɑ�����ĊO�͂����߂��
)�ɑ�����ĊO�͂����߂��
�Ƃ������C�ƂĂ��P���Ȍ��ʂɂȂ�B
���̍ŏ��̎����}-12.21�Ɏ��������C
���R�Ȃ��Ƃ�![]() �����p�ɋ߂Â��ɂ�ĊO�͖͂�����ɂȂ�B
�����őΏۂƂ��Ă���悤�ȕό`����l�ɋN���������͂قڕs�\�����C
�����S����ׂ��Ă݂��Ƃ��ɁC���ϓI�ɂ�
�����p�ɋ߂Â��ɂ�ĊO�͖͂�����ɂȂ�B
�����őΏۂƂ��Ă���悤�ȕό`����l�ɋN���������͂قڕs�\�����C
�����S����ׂ��Ă݂��Ƃ��ɁC���ϓI�ɂ�![]() ����ɂȂ邱�Ƃɂ�
���܂��R�͖����̂ł͂Ȃ����낤���B
�O�͏�Ԃ͏�����f��ԂƓ����ɂȂ��Ă���B
�����������C�}-12.21�̏c����
�P�ʖʐϓ�����̊O�͂�
�e���W�����x���Ƃ����Ƃ�ł��Ȃ��傫�Ȓl�Ɏ��邱�Ƃɂ͒��ӂ���B
����ɂȂ邱�Ƃɂ�
���܂��R�͖����̂ł͂Ȃ����낤���B
�O�͏�Ԃ͏�����f��ԂƓ����ɂȂ��Ă���B
�����������C�}-12.21�̏c����
�P�ʖʐϓ�����̊O�͂�
�e���W�����x���Ƃ����Ƃ�ł��Ȃ��傫�Ȓl�Ɏ��邱�Ƃɂ͒��ӂ���B
�Ō�Ɏ�(12.97)�̑�2 Piola-Kirchhoff���͂�
���߂Ă݂��
�ƂȂ�B����ɑΉ�������Green�̂Ђ��݂����߂�ƁC��(12.9)������
�Ƌ��߂���B�����C��2 Piola-Kirchhoff���͂�Green�̂Ђ��݂�
�����ٕ����̒萔�W���ŊW�t�����\���ޗ��ŁC
�����Łu���������vTruesdell�̉��͑��x��p�����\�����ɓ����ȃ��f����\����
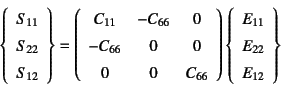
�Ƃ����ޗ��ɑ������邱�ƂɂȂ�B
�ʔ������ƂɁC����Œ�`�ł���ޗ������݂���Ƃ����
����͕s����ł���B
���邢�͋t�ɁC��2 Piola-Kirchhoff���͂�Green�̂Ђ��݂�
�����ٕ����̒萔�W���ŊW�t����
�\����
![]() �ɏ]���ޗ��̏ꍇ�ɂ�
�ɏ]���ޗ��̏ꍇ�ɂ�
�ƂȂ�B�ȒP�̂��߂ɑO�߂ł̗�Ɠ��l�C
![]() �i�����ό`
���_�ɂ�����Hooke�̖@����Poisson�䂪
�i�����ό`
���_�ɂ�����Hooke�̖@����Poisson�䂪![]() �ɑ�������j
�Ƃ����ꍇ�̌��ʂ��}-12.21�Ɏ������B
���͂ƂЂ��݂̒�`�Ɋ܂܂�Ă���^���w�I�Ȕ���`����
���߂ɁC
�ɑ�������j
�Ƃ����ꍇ�̌��ʂ��}-12.21�Ɏ������B
���͂ƂЂ��݂̒�`�Ɋ܂܂�Ă���^���w�I�Ȕ���`����
���߂ɁC![]() ��
��
![]() ���炢�C�܂�20�x���x��
���`�����痣�E���n�߂Ă���B
���������̏ꍇ���C�e���Ђ��݂�����
���炢�C�܂�20�x���x��
���`�����痣�E���n�߂Ă���B
���������̏ꍇ���C�e���Ђ��݂�����![]() %�ɒB���邱�Ƃ͖������낤����C
����قNjC�ɂ���K�v���Ȃ���������Ȃ��B
%�ɒB���邱�Ƃ͖������낤����C
����قNjC�ɂ���K�v���Ȃ���������Ȃ��B
�ł���\�I�ȁC
Mises�̍~��������p�����֘A![]() ���ꑥ�̃��f����p���āC
��{�I�ȑ����e�Y���\�����̋L�q�@��������悤�B
���̐߂ł͑��x��ˑ��Y����ΏۂƂ���̂ŁC���x�Ƒ�������ʂ��Ȃ��B
�Y���̓�������C�Y���Ђ��݂͑���������`�ł����C
���̐ϕ��͗����ˑ��̑㐔�a�ł��������Ȃ����Ƃ���C
���l��͂ɂ����Ă͏������ډ׃X�e�b�v���̑����v�Z������̂��f���ł���B
���������āC�e�����������̏��������͑����ɑ���ω���
��R�����L�q���Ă����������֗��ł���B
�����������ꍇ�ɂ́C�ό`���x�ƃX�s���͎�(12.72)�̂悤��
�e�������ƑY�������ɉ��Z�����ł���
���ꑥ�̃��f����p���āC
��{�I�ȑ����e�Y���\�����̋L�q�@��������悤�B
���̐߂ł͑��x��ˑ��Y����ΏۂƂ���̂ŁC���x�Ƒ�������ʂ��Ȃ��B
�Y���̓�������C�Y���Ђ��݂͑���������`�ł����C
���̐ϕ��͗����ˑ��̑㐔�a�ł��������Ȃ����Ƃ���C
���l��͂ɂ����Ă͏������ډ׃X�e�b�v���̑����v�Z������̂��f���ł���B
���������āC�e�����������̏��������͑����ɑ���ω���
��R�����L�q���Ă����������֗��ł���B
�����������ꍇ�ɂ́C�ό`���x�ƃX�s���͎�(12.72)�̂悤��
�e�������ƑY�������ɉ��Z�����ł���
�������ɐ�������B
�e���͓�����Hooke�̖@�����g���������̂Ƃ������e��
�̎�(12.134)�������ɂ��āC��������������
�Ƃ��������W����������B
��2 Piola-Kirchhoff���͂�Green�̂Ђ��݂͍ޗ��̒�R����
�\���̂ɑ�������Lagrange�I�Ȏړx�ł͂�����̂́C
���̍��W�����̕����I�ȈӖ����\�����Ƃ��Ă͈�������̂ł��邱�Ƃ͑O�q�����B
�����Y�����܂ޏꍇ�ɂ́C���ꑥ�̕����I�����ɂ����updated Lagrange�I��
�����\�������`����̂��]�܂����̂ŁC
�㎮��updated Lagrange�I�ȋɌ����Ƃ邱�Ƃɂ���āC
��(12.118) (12.120) (12.121)��
�p����CTruesdell�̉��͑��x�ƕό`���x�̒e�������Ƃ̊Ԃ�
�Ƃ����C�����ȑ����\������B
���̒e���W��
![]() ���萔�ŁC�����ό`���_�̓����e��Hooke����
�������邽�߂ɂ́C��(3.50)����
���萔�ŁC�����ό`���_�̓����e��Hooke����
�������邽�߂ɂ́C��(3.50)����
�ł���������ƂɂȂ�B
������![]() ��
��![]() �͂��ꂼ�ꂹ��f�e���W���Ƒ̐ϒe���W���ł���B
���邢�͂��̋t�W�́C��(3.55)����
�͂��ꂼ�ꂹ��f�e���W���Ƒ̐ϒe���W���ł���B
���邢�͂��̋t�W�́C��(3.55)����
�ƂȂ�B
���Ď�(12.123)�Ɏ������悤�ɁCTruesdell��
���͑��x�́C�ޗ��ƈꏏ�ɍ��̓I�ɉ�]���鐬���̕�������ł͂Ȃ��C
���ɖc�����Ęc�ސ����̕�����܂�ł���B
�����������̌����ł́C���̍��̓I�ȉ�]���������镔���݂̂�
���グ���C�q�ϓI�ȉ��͑��x�Ƃ���Cauchy���͂�Jaumann���x��
�p�����邱�Ƃ������B
�����ŁC�����ł����̂悤�ɉ��肵�C�㎮(12.154)��
�ƍĒ�`���邱�Ƃɂ���B ���e���I�Ȓe�����f�����炷��C���̉���͋ߎ��ł���B
����Mises�̍~�����́C�L���ό`�̘g�g�ł�
(12.156)
�ŗ^��������B
![]() �͎�(9.22a)��
��`�����������͂ł���B����C���ꑥ�����l��
�͎�(9.22a)��
��`�����������͂ł���B����C���ꑥ�����l��
�ł���B
����ɐ�������
![]() �Ɏ�(12.156a)��������
�Ɏ�(12.156a)��������
(12.158)
��BMises�̍~�������́C�ޗ����ɕ������������������I�ȃ��J�j�Y����
���f�����������̂ł͂Ȃ��B
���������čޗ��Ƌ��ɉ�]����ώ@�҂Ƃ��ė��ꑥ�𑨂���K�v�͖����C
�܂�Cauchy���͂̍X�V�͎�(12.131)�̂悤��Cauchy���͂�
�������W���̉��Z�ł������Ƃ���C�㎮�̐����������P���ȕ���������
��`����������ƂɂȂ�B
��������L���郁�J�j�Y����
��͐�-12.5.4 (4)�Ɏ������B
�������(12.157)�ɑ������
�̂悤�ɁC�Y��������\���ł���B
�����ŁC�e���̍\���W�ƍ��킹�邽�߂ɁCCauchy���͂�
�������W����Jaumann���x�ɒu�������邽�߂ɁC���̒�`���㎮��
������Ă݂悤�B�E�ӂ̉��͂Ɖ��͑����̐ς�
��(12.114)��Jaumann���x�������āC���̒�����
�X�s�����܂ލ�����C
�Ⴆ��
![]() �����o���ƁCCauchy���͂�
�Ώ̐�����
�����o���ƁCCauchy���͂�
�Ώ̐�����
�ƂȂ邱�Ƃ�e�ՂɊm�F�ł���B
���������āC�㎮(12.158a) (12.159)�̉��͑�����Jaumann���x��
�u�������Ă��悭�C����
���Y���̍\�����ɂȂ�B
�ŏI�I�ɁC��(12.155)�̒e�������Ǝ�(12.160)��
�Y����������(12.151)�ɑ�������
�Ƃ��������\���������߂���B
����ɂ��̋t�W��
�ƂȂ�B
�ډ�������(9.39)����
�Ə������Ƃ��ł���B
��{�I�ȃ��f���Ƃ��āC��-9.4.2��
�T��������̔�֘A���ꑥ[60]���Љ�Ă������B
���͂����炪���ŁC��-9.4.2�͂��̔����ό`���_�łł���B
�܂��~����![]() �ƑY���|�e���V����
�ƑY���|�e���V����![]() ��
��
�ƒ�`���Ă���B������
![]() �͎�(9.22a)��
��`�����������͂ł���C
�͎�(9.22a)��
��`�����������͂ł���C![]() �͎�(3.35)��
��`�������͂̑�1�s�ϗʂł���B
�܂��Y���I�̐ςЂ��݂Ƃ���f�Ђ��݂͂��ꂼ��
�͎�(3.35)��
��`�������͂̑�1�s�ϗʂł���B
�܂��Y���I�̐ςЂ��݂Ƃ���f�Ђ��݂͂��ꂼ��
�ƒ�`�����B
�㎮(12.164)�̑Y���|�e���V�������C
���ꑥ�̎�(9.72)�ɑ�������
�Ƃ����W�ɂȂ�B
���ɐ���������
�ƂȂ邱�Ƃ���C��(9.36) (12.165)���l�������
�ƂȂ�B����Ɏ�(12.166)�������Đ��������![]() ��
��
�ƂȂ�B![]() ���d���W��
�ł���B����𗬂ꑥ�̎�(9.133)�ɑ�����߂���
���d���W��
�ł���B����𗬂ꑥ�̎�(9.133)�ɑ�����߂���
�̂悤�ɁC�Y���Ђ��ݑ�����\���ł���B
�����ł���(12.160)�̗U���̂悤�ɁCCauchy���͂�
�������W����Jaumann���x�ɒu�������邱�Ƃ��ł���̂ŁC����
��B
�e���͑O�߂Ɠ��l�C��(12.155)��Hooke����������̂Ƃ���ƁC
���lj��Z���̎�(12.151)����
�ƂȂ�B���l�ɂ��̋t�W��
�ƂȂ�B ���ꂼ��C��(9.144)�Ǝ�(9.145)�� ���͑��x��Cauchy���͂�Jaumann���x�Œu�����������̂ƌ`���I�Ɉ�v����B
��͂�n�Ղ��Ղ̂悤�ɁC������@�������������Ȃ��ޗ�������B
��̃��f���Ƃ��Đ�-9.4.3��
�Љ������[65]������B
���ꑥ�ɁC���͂Ƃ̔����C�܂艞�͑����Ƃ̋�������������
�Ɖ��肵�Ă���B
�~�����ƑY���|�e���V�����͎�(12.164)�Ɠ����ł���B
�U���͐�-9.4.3�ɊT�������̂ŏȗ�����ƁC
�Y���Ђ��ݑ�����
�ƁC�ߎ��I�W�Ƃ��ċ��߂���B
�����ł�
�e���͑O�߂Ɠ��l�C��(12.155)��Hooke����������̂Ƃ���ƁC
���Ǒ��Ђ��ݑ�����
�ƕ\�����B ���ǁC�����\���������́C��(9.150) (9.151)�� ���͑��x��Cauchy���͂�Jaumann���x�ɒu�����������̂ɂȂ�B
�����P�������̓]�ʂ̈ړ��ɂ�萶����
�Y���ό`�z����i�A���̓I�j���ׂ�Ń��f��������Asaro��
���f��[3,5]���Љ�Ă������B
�܂��e���́C�����i�q�ƈꏏ�ɒe���I�ɍ��̉�]�����ώ@�҂���
�����q�ϓI�ȉ��͑��x�ƕό`���x�̊ԂɁC���̒�R�����`���Ă���B
�������CCauchy���͂ł͂Ȃ��CKirchhoff���͂�Jaumann���x��
�����
�ƒ�`���Ă���B
������
�ƒ�`����Ă���B ��(12.123)�Ɏ������悤�ɁCTruesdell�� ���͑��x�͍��̓I�ȉ�]�ƐL�яk�݂���јc�݂ɂ��Cauchy���͂� ������O�C���傤�ǒe�������̊������̂悤�ɗL���Ă��邪�C �㎮(12.176)�ł́C�����i�q�̍��̓I�ȉ�]�Ɗi�q�Ԋu�� �L�яk�݂ɂ���̕�������l���������͑��x�ŁC �e����R�������`���Ă��邱�ƂɂȂ�B �܂�C�����i�q���W�O�U�O�ɂȂ�e���͂قږ����ł�����̂ƍl���Ă���B
����ɑ��Y���ό`�́C
�]�ʂ̈ړ��ɂ���Č����i�q�ʁiBurgers�x�N�g���j��������
�Y�����邢�͂��ׂ�ό`���A���I�ɕ��z�E�~�ς���12.28���̂Ƃ��ă��f��������Ă���B
�܂�}-12.22�Ɏ������悤�ɁC
�P�ʖ@���x�N�g����
![]() �Ƃ���
�Ƃ���![]() ���ׂ�ʏ��
���ׂ�ό`����
���ׂ�ʏ��
���ׂ�ό`����
![]() �������悤�Ƃ��Ă���ƍl����B
�������
�������悤�Ƃ��Ă���ƍl����B
�������
![]() �͔�t�I�ȕό`12.29�ƍl���C�P�ʕ����x�N�g��
�͔�t�I�ȕό`12.29�ƍl���C�P�ʕ����x�N�g��
![]() ��
�t�����̂��ׂ�n�������ɑ��݂�����̂Ƃ���B
���̂Ƃ��C����
��
�t�����̂��ׂ�n�������ɑ��݂�����̂Ƃ���B
���̂Ƃ��C����![]() ���ׂ�n�ɐ����邷�ׂ葝���ɂ����
���ׂ�n�ɐ����邷�ׂ葝���ɂ����
�̂悤�ȑY���I�ȑ��x���z��������������B
�����ł͓Y����![]() �͎O����Ă��邱�Ƃ���C
���̑��a�͂Ƃ�Ȃ��B
�͎O����Ă��邱�Ƃ���C
���̑��a�͂Ƃ�Ȃ��B![]() �͑��݂��邷�ׂ�n�̐��ł���C
�����\���ɂ���Ă��̌����Ɛ��͌��܂�B
�Ⴆ�ΐ}-9.16�̖ʐS�������̗���Q�Ƃ��ė~�����B
�]�ʂ͎~�܂��Ă���Ƃ��ɂ͉����ό`�������Ȃ����C
���ꂪ�ړ����邱�Ƃɂ���Ĕ�t�ό`�������邽�߁C���ꂪ���x���z���
�����Ń��f��������Ă���B���������āC�ό`���x�ƃX�s���̑Y��������
�͑��݂��邷�ׂ�n�̐��ł���C
�����\���ɂ���Ă��̌����Ɛ��͌��܂�B
�Ⴆ�ΐ}-9.16�̖ʐS�������̗���Q�Ƃ��ė~�����B
�]�ʂ͎~�܂��Ă���Ƃ��ɂ͉����ό`�������Ȃ����C
���ꂪ�ړ����邱�Ƃɂ���Ĕ�t�ό`�������邽�߁C���ꂪ���x���z���
�����Ń��f��������Ă���B���������āC�ό`���x�ƃX�s���̑Y��������
(12.179)
�ƂȂ�B������![]() �́C
�́C![]() �̂��ׂ�n�̂����������悤�Ƃ��Ă���
�i��q����ډ���������j���ׂ�n�ɑ��Ă̂ݑ��a���Ƃ���̂Ƃ���B
�܂�
�̂��ׂ�n�̂����������悤�Ƃ��Ă���
�i��q����ډ���������j���ׂ�n�ɑ��Ă̂ݑ��a���Ƃ���̂Ƃ���B
�܂�
�ƒ�`����Ă���B������![]() �ɂ��Ă͑��a���Ƃ�Ȃ��B
�ȉ��C���ׂ�n�ɂ��Ă̓Y�����ɂ��ẮC���a���Ƃ�Ƃ��͑��a�L����
�������邱�Ƃɂ���B
�]�ʂ��ړ����Ă������i�q�͉�]���Ȃ����낤����C����
�ɂ��Ă͑��a���Ƃ�Ȃ��B
�ȉ��C���ׂ�n�ɂ��Ă̓Y�����ɂ��ẮC���a���Ƃ�Ƃ��͑��a�L����
�������邱�Ƃɂ���B
�]�ʂ��ړ����Ă������i�q�͉�]���Ȃ����낤����C����
![]() ��
�e���I�ȃX�s�������ēK�������邽�߂ɐ����Ă�����̂Ɖ��߂���B
���������āC���ׂ�ʂ̉^���͒e���I�ɂ��������Ȃ����̂Ƃ�
��
�e���I�ȃX�s�������ēK�������邽�߂ɐ����Ă�����̂Ɖ��߂���B
���������āC���ׂ�ʂ̉^���͒e���I�ɂ��������Ȃ����̂Ƃ�
�̂悤�ȒP���ȉ�]�^���������Ȃ����̂Ƃ���B
����ɂ���āC��̃x�N�g��
![]() ��
��
![]() ��
�P�ʃx�N�g���̂܂܂ɂȂ�̂ł킩��Ղ��B
��
�P�ʃx�N�g���̂܂܂ɂȂ�̂ł킩��Ղ��B
���Ƃ͍~�������Ɨ��ꑥ���`����C�e�Y���\���������f�����ł���B
����͊e���ׂ�n�ɂ����門�C�Ƃ��ׂ�Ń��f��������̂��ł��f����
�P���ł���B
�܂�C����![]() ���ׂ�n�̂��ׂ�ʏ�̂���f���͂�
����K���l
���ׂ�n�̂��ׂ�ʏ�̂���f���͂�
����K���l
![]() �ɒB�����Ƃ��C�܂�
�ɒB�����Ƃ��C�܂�
�������Ƃ��ɓ]�ʂ������n�߂���̂Ƃ���B
����
![]() �͍ő喀�C�͂ɑ�������ޗ��p�����[�^�ł���B
�܂��C���ꑥ�͂���ɑΉ����āC���̂��ׂ�ʏ��Schmid��
�ŗ^����B����͏㎮(12.182)�̕ω����ɑ�����
�͍ő喀�C�͂ɑ�������ޗ��p�����[�^�ł���B
�܂��C���ꑥ�͂���ɑΉ����āC���̂��ׂ�ʏ��Schmid��
�ŗ^����B����͏㎮(12.182)�̕ω����ɑ�����
�ƃ��f��������Ă���B����
![]() ��
��![]() �n��
���ׂ葝���ɂ����
�n��
���ׂ葝���ɂ����![]() �n�ɐ����邷�ׂ��R�͑�����^����ޗ�
�p�����[�^�ŁC�����C�W���ɑ���������̍d���W���ł���B
�n�ɐ����邷�ׂ��R�͑�����^����ޗ�
�p�����[�^�ŁC�����C�W���ɑ���������̍d���W���ł���B
![]() ��
�����̕����I�ȈӖ��ɂ��Ă͕������Q�Ƃ��ė~�����B
��
�����̕����I�ȈӖ��ɂ��Ă͕������Q�Ƃ��ė~�����B
��(12.182)�����������
�ƂȂ�̂ŁC���ׂ�ʂ̉^���̎�(12.181)�������Đ��������
�ƂȂ�B�܂莮(12.177)���Q�Ƃ���C���̊W��
�ƕ\�����Ƃ��ł���B
�܂�C�����i�q�ƈꏏ�ɉ�]���Ȃ���ώ@�������ꑥ�ɂȂ��Ă��āC
��������(12.158)��Prandtl-Reuss���f���̐��������ƈقȂ�B
���̌��ʂ��CCauchy���͂̑Ώ̐��Ȃ�Ȃ��悤��
��`�������Ď�(12.183)�ɑ������C���ꑥ��
�ƕ\�����B���l�ɁC�~��������(12.182)��
�Ə����������Ƃ��ł���B
���������āC����![]() ���ׂ�n�ɑ���ډׁE���ׂ̏�����
���ׂ�n�ɑ���ډׁE���ׂ̏�����
�̂悤�ɋK�肷��������Ƃ��킩��B
���āC
��(12.184)�̗��ꑥ�̍��ӂɎ�(12.176)�̒e���W��
������C�ό`���x�̉��Z���̎�(12.151)������ɓK�p�����
�ƂȂ�B����Ɏ�(12.179a)�̕ό`���x�̑Y��������
�^���w��������C���ǎ�(12.184)����
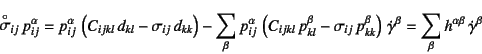
�Ƃ����W��B
�ډ�������������Ă���ꍇ�ɂ́C���̎����炷�ׂ葝����
�Ƌ��߂���B������
![]() �͎���
�͎���
![]() �̋t�s��ł���B
�̋t�s��ł���B
�܂��C�e���̎�(12.176)��
�ό`���x�̉��Z���̎�(12.151)�𗘗p�����
�ƂȂ�B����2��(12.187) (12.189)����
�C���ꂪ�P�����̂̑����e�Y���\�����̈�̕\���ɂȂ�B
�Ȃ��C���̃��f���̑Y���ό`�͂����܂ł��]�ʂ̒~�ς� �A���̒��ɕ��z���������ׂ�Ń��f�����������̂ł���B���������� ����𑽌����̂̃V�~�����[�V�����ɗp���āC���͏W�����ŗ��E�� �Y���ό`���W�������Ƃ��Ă��C���ۂɊE�ʂŐ�����ł��낤 ��T������f�����ł��Ă���Ƃ͌���Ȃ��B �����ł́C�̔����ƒP�������̍��̓I�ȉ�]12.30�������Ă���� �l�����邪�C���������Asaro�̃��f���œK�ɃV�~�����[�V�����ł���Ƃ� ����Ȃ��̂Œ��ӂ��K�v�ł���B
�ЂƂ������ʂЂ��ݖ��ł��������������f��
�̗�[43]��
�����Ă������B�}-12.23�̃C���Z�b�g��
����悤�ɁC�P��������ȉ~�`�ŋߎ����C�e�������ɂ͋��ފp70�x�œ��
���ׂ���i���������Ďl�̂��ׂ�n![]() �`4�j�݂̂�����Ƃ���B
���̌������̌�����0�x����90�x�܂ł�2�x���݂�46��ޓ��Ԋu��
���z���Ă�����̂Ƃ���B
�e���������̔����I�ȍ\�����͂��̐߂Ŏ��������f���ŗ^��������̂Ƃ��C
��(12.182)�̊�l
�`4�j�݂̂�����Ƃ���B
���̌������̌�����0�x����90�x�܂ł�2�x���݂�46��ޓ��Ԋu��
���z���Ă�����̂Ƃ���B
�e���������̔����I�ȍ\�����͂��̐߂Ŏ��������f���ŗ^��������̂Ƃ��C
��(12.182)�̊�l
![]() ���d�����܂܂�
���d�����܂܂�
�ƈ��ł���Ƃ���B
����ɑ������̂Ƃ��Ă̕��ϋ����́C
��͓I�ȕ��ω���@��L���ό`�������_�Ɋg���������̂�
���f���������B�㎮��
![]() �́C���̎�@��p����
�������̂̕��ϓI�Ȃ���f�e���W���ł���B����ɑ�
�́C���̎�@��p����
�������̂̕��ϓI�Ȃ���f�e���W���ł���B����ɑ�![]() �������ւ�
�P���ډׂɂ���ĕω�����~���Ȗʂ�͎��I��12.31��������
���}-12.23�ł���B
�P�����Ԃ̑��ݍ�p����͓I���ω���@�ōl���ł��Ă���̂ŁC
�����ɂقړ����ʼn~��̍~���Ȗʂ��ډׂɔ����čډו����ɐ���Ă����C
���͏�Ԃ̕ω��ɂ���ړ��d��
���������B
�܂��~���Ȗʂ́C��(12.182)�Œ�`���ꂽ�S���ׂ�n��
�~�������̒��̍ŏ��������瓾���邽�߁C�܂����ɂȂ�B
���������č~���ȖʂɊp�_�������邪�C���̊p�_�ł�
�Ή�������̂��ׂ肪�\�ɂȂ邾���ŁC���E�l���̉��Ƃ��Ă�
�B��ɑY���ό`������ł���i�̂ł��낤�ƍl���Ă���j�B
�|�̂悤�ɖ����̒P�������̏W���̂ł���ꍇ�ɂ́C���̊p�_�͖����Ȃ�
���炩�ȍ~���ʂɂȂ�ƍl��������B
�������ւ�
�P���ډׂɂ���ĕω�����~���Ȗʂ�͎��I��12.31��������
���}-12.23�ł���B
�P�����Ԃ̑��ݍ�p����͓I���ω���@�ōl���ł��Ă���̂ŁC
�����ɂقړ����ʼn~��̍~���Ȗʂ��ډׂɔ����čډו����ɐ���Ă����C
���͏�Ԃ̕ω��ɂ���ړ��d��
���������B
�܂��~���Ȗʂ́C��(12.182)�Œ�`���ꂽ�S���ׂ�n��
�~�������̒��̍ŏ��������瓾���邽�߁C�܂����ɂȂ�B
���������č~���ȖʂɊp�_�������邪�C���̊p�_�ł�
�Ή�������̂��ׂ肪�\�ɂȂ邾���ŁC���E�l���̉��Ƃ��Ă�
�B��ɑY���ό`������ł���i�̂ł��낤�ƍl���Ă���j�B
�|�̂悤�ɖ����̒P�������̏W���̂ł���ꍇ�ɂ́C���̊p�_�͖����Ȃ�
���炩�ȍ~���ʂɂȂ�ƍl��������B