 |
最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
ここでは代表的なモデルをいくつか紹介するが, いずれのモデルも,観察される巨視的な挙動を巨視的な物理量で 表現する現象論的9.31な記述 になっている。そのため,材料内部の微視構造の影響が直接には反映されておらず, 例えば, いわゆる寸法効果 と密接に関係する材料内部の特性長さ 9.32等を考慮できない。これを考慮するために, 非局所理論の近似としてひずみ勾配を用いた定式化等も考えられているが, それは本質的な解決法ではない。
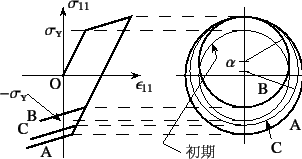
前節までの基本的なモデルでは,硬化は降伏曲面の半径が大きくなる
だけであり,変形履歴の関数ではあるが,履歴がスカラー量で
表現されているために,図-9.37のAのように,
その半径はすべての応力方向に同じだけ大きくなるものであった。
つまり,ある方向に載荷をして硬化によって降伏応力が大きくなった場合,
そこから除荷して異なる方向に載荷を継続した場合にも,
その大きくなった降伏応力までは降伏しないことになる。
したがって,このような硬化を等方硬化
と呼んでいる。
しかし,この章の最初の実験観察の節で述べたように,
実際にはBauschinger効果
が存在し,過去に経験した載荷の向きと逆向きの載荷では,
その時点での降伏応力よりも小さい応力レベルで降伏が始まることがある。
このような効果を考慮するための一つの
方法として,図-9.37のBやCのように,
降伏曲面の中心座標![]() が移動するモデルが考えられた。
このような硬化を移動硬化
と呼んでいる。図-9.37のBは
降伏曲面の半径が変わらず移動硬化のみを含むもので,Cは
移動硬化と等方硬化の両方を含むものである。
が移動するモデルが考えられた。
このような硬化を移動硬化
と呼んでいる。図-9.37のBは
降伏曲面の半径が変わらず移動硬化のみを含むもので,Cは
移動硬化と等方硬化の両方を含むものである。
まず,降伏曲面の中心座標![]() を導入し,これが変形に
伴って移動できると考え,降伏関数の
を導入し,これが変形に
伴って移動できると考え,降伏関数の![]() を変更して
を変更して
と定義し直そう。ここに![]() は
は![]() の偏差成分である。
つまり,応力そのものの偏差成分ではなく,変形履歴途中の
任意の降伏曲面の中心からの
相対的な応力成分の偏差成分で定義されるせん断成分で降伏が
支配されるとする。
ただしここでは,ひとまずは等方硬化を除外し,
の偏差成分である。
つまり,応力そのものの偏差成分ではなく,変形履歴途中の
任意の降伏曲面の中心からの
相対的な応力成分の偏差成分で定義されるせん断成分で降伏が
支配されるとする。
ただしここでは,ひとまずは等方硬化を除外し,![]() は定数とする。
その代わりに,中心座標が塑性変形の変化と累積によって移動するものとする。
また流れ則は式(9.61)と同じく
は定数とする。
その代わりに,中心座標が塑性変形の変化と累積によって移動するものとする。
また流れ則は式(9.61)と同じく
が成立するものとする。式(9.111)の定義から
という関係にある。
まず整合条件をとると,式(9.111)の全微分から
となる。つまり,図-9.38に示したように,
応力増分の降伏曲面の法線方向成分の大きさは,
降伏曲面の移動増分の同じ方向成分と同じでなければ
ならず,したがって,
![]() となるか,
相対的な
応力増分の成分
となるか,
相対的な
応力増分の成分
![]() が
移動する降伏曲面の接線方向にしか変化できないことを示している。
降伏条件と流れ則はこれまでとほぼ同様に定義できているが,
まだ降伏曲面の中心
が
移動する降伏曲面の接線方向にしか変化できないことを示している。
降伏条件と流れ則はこれまでとほぼ同様に定義できているが,
まだ降伏曲面の中心![]() の発展則が規定されていない。
これには主に次の二つの考え方が用いられる。
の発展則が規定されていない。
これには主に次の二つの考え方が用いられる。
Pragerは,降伏曲面の中心は塑性ひずみ増分の方向,つまり,
降伏曲面の法線方向に移動すると仮定した。
これは近年使われる多曲面モデルの運動学の基礎になっていると思われる。
すなわち
としたため,式(9.112)の流れ則と式(9.113)を
代入すると
と仮定したことになる。
これを整合条件式(9.114)に代入すれば
となる。ここに,
![]() は硬化係数で
は硬化係数で
と定義される。
この![]() を流れ則に代入すれば,最終的に塑性ひずみ増分が
を流れ則に代入すれば,最終的に塑性ひずみ増分が
と求められる。
したがって,降伏曲面の中心点の移動則(![]() の発展則)も
の発展則)も
と表現できる。 このモデルの中心の移動は,塑性ひずみ増分と同様に,静水圧では生じない。 しかし,なぜ移動硬化が生じるかについて材料の微視的挙動を 考えると,例えば金属塑性ならば,内部に存在する何らかの微視構造のために, ある方向の塑性変形によって移動した転位が 逆向きの塑性変形においては移動できなくなることが原因ではないかと 推測される。 そのような微視構造がある材料では,巨視的な静水圧載荷に対しても 微視的な硬化が発生することは容易に推測できるのだが。
そこで,もう少し一般性を持たせるために,
中心座標が式(9.26)で定義された
累積塑性ひずみの関数として変化すると仮定しよう。つまり
とするのである。
式(9.114)の整合条件はさらに
となる。式(9.26)の累積塑性ひずみの定義に
流れ則の式(9.112)を代入して,
式(9.113)を考慮すれば
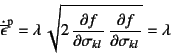
になるので
と求められる。
したがって,再度流れ則にこれを代入して整理すると,塑性ひずみ増分は
と求められる。実はこれは,Pragerモデルの式(9.118)と
形式的には一致している。またこれは,Prandtl-Reussの
式(9.44)ともよく整合しており,
単に応力の中心を![]() だけずらしたものである。
だけずらしたものである。
ここまでではまだ,中心の移動則,
つまり移動の発展則が定義されていない。Zieglerはそれを
と仮定した。![]() は流れ則の
は流れ則の![]() のようなパラメータである。
この仮定を式(9.114)の整合条件に代入すると
のようなパラメータである。
この仮定を式(9.114)の整合条件に代入すると
となる。式(9.113)を用いると,上式(![]() )右辺は
)右辺は
となるので,結局,上式(![]() )から
)から
と求められる。これを上の仮定に代入すれば
と求められる。この法則とPragerのモデル式(9.119)との
違いは,中心の移動量が偏差成分だけではないことである。
これは,式(9.116)のPragerの仮定と
式(9.123)のZieglerの仮定の間の

といった違いに原因がある。
最後に逆関係を求めておく。弾性はHookeの法則に従うものとすれば,
式(3.54)が成立するので,
それと式(9.122)を加算則の式(9.21)に代入して,
総ひずみ増分は
となる。節-9.2.3で
説明した手法で逆関係を求めると
と求められる。
ここに![]() は式(9.49)で定義したスィッチである。
この方程式と式(9.124)が,
移動硬化則の増分型構成方程式になる。
は式(9.49)で定義したスィッチである。
この方程式と式(9.124)が,
移動硬化則の増分型構成方程式になる。
より現実的なモデルは,前節の移動硬化則と等方硬化則を共に考慮したものであろう。
ここではZieglerの考え方を用いることにする。
まず式(9.111)の降伏関数を
のように,降伏応力も累積塑性ひずみの関数とする。
こうすることで,整合条件が
となる。式(9.112)の流れ則を代入し,
式(9.37b) (9.121)の硬化係数の定義を用いると
を得る。これを流れ則に代入すれば,ひずみ増分の塑性成分が
と求められる。中心の移動についても,前節同様の演算を行うと
となる。![]() の場合が前節のZieglerモデルの結果と一致する。
の場合が前節のZieglerモデルの結果と一致する。
節-9.3.3で用いた例を
ここでも使って,Zieglerの移動硬化モデルも含む場合の,
線形硬化の数値例を示しておこう。
簡単のために材料も節-9.3.3と同じく,
普通鋼を念頭に置いて![]() GN/m
GN/m![]() ,
, ![]() ,
,
![]() ,
,
![]() MPaとし,
移動硬化については
MPaとし,
移動硬化については![]() と設定することによって
移動の様子が誇張されるようにした。
応力も同様に
と設定することによって
移動の様子が誇張されるようにした。
応力も同様に
![]() と
と
![]() の2軸状態とし,
載荷パターンも図-9.25に示したのと同じ3種類とする。
それに伴い,降伏曲面の中心位置も
の2軸状態とし,
載荷パターンも図-9.25に示したのと同じ3種類とする。
それに伴い,降伏曲面の中心位置も
のみを考えればいいことになる。
こうすることによって,
関係式のほとんどが,節-9.3.3の![]() と
と![]() を
を
のように置き換えれば得られることもわかる。降伏曲面の中心座標の
発展則だけを明記しておくと
となる。
明らかに積分不可能であり,中心座標の移動も履歴依存であることがわかる。
数値例では,
![]() の比例載荷からの3種類の
さらなる応力載荷を対象とし,具体的には
の比例載荷からの3種類の
さらなる応力載荷を対象とし,具体的には
のような履歴とした。
結果的に生じた相当塑性ひずみは約2%(
![]() )であった。
)であった。
図-9.39が,降伏後の応力ひずみ関係の例である。
履歴依存で最終状態が異なっているのがわかる。
増分ステップは![]() から
から![]() までを用いて結果を比較したが,
この図の応力ひずみ関係で判別できるような差は生じなかった。
しかし,単純な増分解析で降伏条件に蓄積される誤差はステップ数によって
異なる。これを示したのが図-9.40である。
相対誤差では有効数字3桁を確保していることが明らかなので,
応力ひずみ関係の図に顕著な差が生じないのも当然であろう。
そもそも履歴依存の増分理論なので,増分解析で十分な精度の解が
得られるのは工学的には好ましい結果である。
降伏曲面の移動を表したのが図-9.41である。
原点から伸びている線分が,降伏曲面の中心
までを用いて結果を比較したが,
この図の応力ひずみ関係で判別できるような差は生じなかった。
しかし,単純な増分解析で降伏条件に蓄積される誤差はステップ数によって
異なる。これを示したのが図-9.40である。
相対誤差では有効数字3桁を確保していることが明らかなので,
応力ひずみ関係の図に顕著な差が生じないのも当然であろう。
そもそも履歴依存の増分理論なので,増分解析で十分な精度の解が
得られるのは工学的には好ましい結果である。
降伏曲面の移動を表したのが図-9.41である。
原点から伸びている線分が,降伏曲面の中心![]() の軌跡である。
一点鎖線と白丸がs2tの結果であり,破線と白四角がt2s,実線と
黒丸が比例載荷の結果を示している。
最終応力状態が同じであっても,履歴の影響を受けて降伏曲面の位置も
異なるのが明らかになっている。
の軌跡である。
一点鎖線と白丸がs2tの結果であり,破線と白四角がt2s,実線と
黒丸が比例載荷の結果を示している。
最終応力状態が同じであっても,履歴の影響を受けて降伏曲面の位置も
異なるのが明らかになっている。
鋼の場合には平均応力が降伏に及ぼす影響は非常に小さいが,
砂や粘土のように必ずしも連続体として取り扱うことができ難い材料や,
岩や複合材料のように内部に微視構造を持つ材料の場合には,
平均応力つまり静水圧が降伏や塑性変形に影響を及ぼす。
ここでは非関連流れ則
の代表的な例としてDrucker-Pragerモデル
[21]を一般化したもの[60]を考えてみよう。
そこでは,降伏関数![]() と塑性ポテンシャル
と塑性ポテンシャル![]() を
を
(9.130)
と定義している。ここに
![]() は式(9.22a)で
定義した相当応力であり,
は式(9.22a)で
定義した相当応力であり,![]() は式(3.35)で
定義した応力の第1不変量である。静水圧は
は式(3.35)で
定義した応力の第1不変量である。静水圧は
で定義できるので,これを静水圧依存のモデルと呼ぶことがある。
履歴を代表するパラメータとしては,前節までの
取り扱いと同様,累積塑性ひずみを用いるのが相応しいが,
ここでは塑性的な体積変形も存在するため,
式(9.26)の累積塑性ひずみは,
塑性ひずみ増分の偏差成分のみで定義し直す必要がある。したがって
と定義した。
![]() は,
前節まででは考える必要の無かった体積変形の塑性成分9.33
である。もし
は,
前節まででは考える必要の無かった体積変形の塑性成分9.33
である。もし
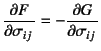 の場合には
関連流れ則になる。
上式では
の場合には
関連流れ則になる。
上式では![]() は
は![]() のみの関数としているが,
のみの関数としているが,![]() と同様,
もっと一般的に
と同様,
もっと一般的に
![]() 等の関数と考えてもいい。
等の関数と考えてもいい。
(9.133)
という関係になる。この関係から,せん断変形と体積変形の塑性成分がそれぞれ
となる。このことから,パラメータ![]() は「塑性的な体積膨張」に
関する材料パラメータであることがわかる。
は「塑性的な体積膨張」に
関する材料パラメータであることがわかる。
次に整合条件は
となることから,式(9.36)を考慮すれば
となる。式(9.134)を式(9.135)の右辺に代入して
整理すると
という関係を得ることができることから,![]() が
が
(9.136)
となる。![]() は硬化係数
である。これを流れ則の式(9.133a)に代入し戻せば
は硬化係数
である。これを流れ則の式(9.133a)に代入し戻せば
(9.137)
のように,塑性ひずみ増分を表現できる。
ここに![]() (符号に注意)は,降伏関数に平均応力が及ぼす影響を代表する
材料パラメータである。
(符号に注意)は,降伏関数に平均応力が及ぼす影響を代表する
材料パラメータである。
ところで式(9.130a)の降伏関数と式(9.137b)の![]() の
定義を眺めると,Drucker-Prager[19,21]
の降伏条件の
の
定義を眺めると,Drucker-Prager[19,21]
の降伏条件の
における![]() と上の
と上の![]() が対応(
が対応(![]() の
の![]() によるTaylor展開の
定数項に一致)していることがわかる。
一方,内部摩擦角という概念がある地盤材料でよく用いられるMohr-Coulombの
破壊規準
は
によるTaylor展開の
定数項に一致)していることがわかる。
一方,内部摩擦角という概念がある地盤材料でよく用いられるMohr-Coulombの
破壊規準
は
あるいは
| (9.139) |
と表される。
あるいは式(9.56)のLode角
![]() を用いると
を用いると
| (9.140) |
と表す[57]こともできる。ここに![]() は粘着力
であり,
は粘着力
であり,![]() は内部摩擦角
であり,
は内部摩擦角
であり,
![]() と
と
![]() は主応力の最大値と最小値である。
降伏条件の概念のところで説明に使った摩擦に関する条件そのものである。
この両者を比べると,Drucker-Pragerモデルの
材料パラメータ
は主応力の最大値と最小値である。
降伏条件の概念のところで説明に使った摩擦に関する条件そのものである。
この両者を比べると,Drucker-Pragerモデルの
材料パラメータ![]() と
と![]() は,Mohr-Coulombの
破壊規準の
は,Mohr-Coulombの
破壊規準の![]() と
と![]() との間に
との間に
という(近似)関係がある[19,100]とされている。
![]() 度で
度で
![]() 程度に
相当する。Mohr-Coulombの
破壊規準が角のある破壊規準面(降伏曲面)になるので,
それを滑らかに近似したものがDrucker-Pragerの降伏条件と
解釈する[19]こともできる。
程度に
相当する。Mohr-Coulombの
破壊規準が角のある破壊規準面(降伏曲面)になるので,
それを滑らかに近似したものがDrucker-Pragerの降伏条件と
解釈する[19]こともできる。
一方,ここのモデルを関連流れ則にすると![]() は
は![]() と同じになり,
式(9.141)で定義されることになるが,
特に地盤材料にそれを用いた場合には,
塑性的な体積膨張が実測値より大きくなることが多い[19]とされている。
そのため,地盤材料の場合には非関連流れ則とした上で
と同じになり,
式(9.141)で定義されることになるが,
特に地盤材料にそれを用いた場合には,
塑性的な体積膨張が実測値より大きくなることが多い[19]とされている。
そのため,地盤材料の場合には非関連流れ則とした上で![]() を
式(9.141)と同様に定義するものの,内部摩擦角
を
式(9.141)と同様に定義するものの,内部摩擦角![]() の代わりに
ダイレタンシー角
と呼ばれる別の角度
の代わりに
ダイレタンシー角
と呼ばれる別の角度![]() (
(![]() )を用いることが多い。
)を用いることが多い。
例えば![]() が定数の場合には,式(9.130a)から
降伏条件を
が定数の場合には,式(9.130a)から
降伏条件を
と書くことができるので,例えば等方応力![]() と
せん断応力
と
せん断応力
![]() の関係として初期降伏条件を
眺めたとすると図-9.42の上図のようになる。
あるいは3次元の主応力空間で描くと,下図のような,
等方応力の正方向にとがった円錐状の降伏曲面に相当する。
引張り側には等方応力状態であっても降伏曲面が存在するが,
圧縮側では降伏しない。
では,この円錐の先端Pではどうなっているのか調べておこう。
初期降伏の場合には,そこの応力状態は単純に
の関係として初期降伏条件を
眺めたとすると図-9.42の上図のようになる。
あるいは3次元の主応力空間で描くと,下図のような,
等方応力の正方向にとがった円錐状の降伏曲面に相当する。
引張り側には等方応力状態であっても降伏曲面が存在するが,
圧縮側では降伏しない。
では,この円錐の先端Pではどうなっているのか調べておこう。
初期降伏の場合には,そこの応力状態は単純に
となるため,式(9.137a)からは
のように,塑性的体積膨張しか生じないことになる。
したがって,もしパラメータ![]() が零であれば,
この応力状態では塑性変形は生じないことになる。
降伏曲面の角点のように見えるが,せん断応力成分が存在しないことから
特に問題は生じない。
が零であれば,
この応力状態では塑性変形は生じないことになる。
降伏曲面の角点のように見えるが,せん断応力成分が存在しないことから
特に問題は生じない。
少し具体的な降伏曲面を示すために,節-9.3.3と
同様に,軸力を作用させた円筒供試体のねじり試験のような
応力状態の
![]() と
と
![]() の2軸状態を
調べておこう。
これは代入すれば容易に求めることができるので,結果だけを
示しておくと,まず
の2軸状態を
調べておこう。
これは代入すれば容易に求めることができるので,結果だけを
示しておくと,まず
![]() の場合には楕円形の
の場合には楕円形の
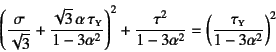
となる。また
![]() の場合には放物線
の場合には放物線
になる。さらに
![]() の場合には双曲線
の場合には双曲線
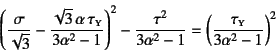
となる。これは図-9.42の
円錐表面と
![]() -
-
![]() 面との
交線であり,図-9.43に
示したように,
面との
交線であり,図-9.43に
示したように,![]() が大きくなると圧縮側に降伏曲面が存在しなくなる。
これはゴムのような材料のモデルにも利用できそうだ。
が大きくなると圧縮側に降伏曲面が存在しなくなる。
これはゴムのような材料のモデルにも利用できそうだ。
あるいは,式(9.133a)の流れ則で算定される
塑性ひずみ増分の成分を用いて,塑性的な平面ひずみ
条件を
に加えて
と定義して,この平面ひずみ状態における降伏曲面を求め,
塑性的な体積膨張に関するパラメータ![]() の影響を把握しておこう。
上式(9.143)が成立するためには
の影響を把握しておこう。
上式(9.143)が成立するためには
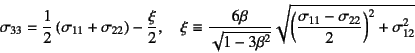
という関係を得る。![]() の場合のこの式を弾性の
平面ひずみの式(3.110)と比べると,
一見して
の場合のこの式を弾性の
平面ひずみの式(3.110)と比べると,
一見して![]() にしたように見える。
これは,塑性変形には体積変形が無い(
にしたように見える。
これは,塑性変形には体積変形が無い(![]() の材料特性と同)
からである。
この関係から
の材料特性と同)
からである。
この関係から
となり,相当応力と平均応力は
と表される。
これから
![]() ,
,
![]() で他の応力成分が零の場合の降伏条件は
で他の応力成分が零の場合の降伏条件は
となり,それを図-9.44に示した。
定式化から
でなければならず,また![]() が望ましいとされているが,
この図から,
が望ましいとされているが,
この図から,![]() が降伏曲面を圧縮側に移動させようとするのに対し,
特に
が降伏曲面を圧縮側に移動させようとするのに対し,
特に![]() が大きい場合には,
塑性的な体積膨張に関するパラメータ
が大きい場合には,
塑性的な体積膨張に関するパラメータ![]() は降伏曲面の半径を
減少させる効果を有していることがわかる。
は降伏曲面の半径を
減少させる効果を有していることがわかる。
弾性はHookeの法則に従うものとすれば,
式(3.54)を満足する。
したがって総ひずみ増分は,これと式(9.137a)を
加算則の式(9.21)に代入して
となる。ここに![]() は式(9.49)で定義した
スィッチである。節-9.2.3で
説明した手法で逆関係を求めると
は式(9.49)で定義した
スィッチである。節-9.2.3で
説明した手法で逆関係を求めると
という関係を得る。
砂や岩のように,内部に空隙や欠陥・節理があるような材料では, 巨視的な材料試験レベルでも,必ずしも法線則が成立するとは限らない。 つまり,降伏曲面の法線方向のみにではなく,その接線方向にも応力増分に 依存した塑性ひずみ増分の成分が存在すると考えることがある。 ここでは,その代表的なモデル[65]について説明する。 降伏曲面での法線則を緩和していることから, このモデルは降伏曲面が角点 を持つような材料の,取り扱い易い近似モデルの一つとしても知られている。
流れ則の基本的な部分については,前節の静水圧依存のモデルで与えられる
ものとする。提案されたモデルでは,降伏曲面の接線方向の塑性ひずみ増分を
の方向成分で与える。
重要なのは,この成分が仕事をしないということである。
つまり上式に![]() を乗じて
を乗じて![]() ,
, ![]() についての総和をとると,
式(9.22a)を考慮すれば
についての総和をとると,
式(9.22a)を考慮すれば
となることに注意する。
つまり式(9.58)のDruckerの安定公準に関与しない
一種の不安定項である。
これを流れ則の式(9.72)に
加えることによって,新たな流れ則は
で与えられるものとする。ここに![]() は,非共軸性
に関する材料パラメータである。
このように,塑性ひずみ増分が応力増分方向の成分を持つ(式(9.146)の
右辺に添え字
は,非共軸性
に関する材料パラメータである。
このように,塑性ひずみ増分が応力増分方向の成分を持つ(式(9.146)の
右辺に添え字![]() を持つ応力増分成分項が存在する)ことになり,
式(9.32)で示した共軸性を満足していない。
したがって,これを非共軸モデルと呼ぶことがある。
塑性にも弾性と同じような抵抗成分を追加したものと考えてもいい。
また上式(
を持つ応力増分成分項が存在する)ことになり,
式(9.32)で示した共軸性を満足していない。
したがって,これを非共軸モデルと呼ぶことがある。
塑性にも弾性と同じような抵抗成分を追加したものと考えてもいい。
また上式(![]() )は偏差応力
)は偏差応力![]() との積でも成立することから,
上式(9.146)の第2項の塑性ひずみ増分の非共軸
成分
との積でも成立することから,
上式(9.146)の第2項の塑性ひずみ増分の非共軸
成分
![]() は偏差応力と直交する。
したがって,
もし関連
は偏差応力と直交する。
したがって,
もし関連![]() 流れ則で基本的な塑性変形がモデル化された場合には,
上式(9.146)の第1項の
塑性ひずみ増分のPrandtl-Reuss成分
流れ則で基本的な塑性変形がモデル化された場合には,
上式(9.146)の第1項の
塑性ひずみ増分のPrandtl-Reuss成分
![]() が
式(9.30)にあるように偏差応力と平行であることから,
結局,塑性ひずみ増分の非共軸な
成分
が
式(9.30)にあるように偏差応力と平行であることから,
結局,塑性ひずみ増分の非共軸な
成分
![]() はPrandtl-Reussの
成分
はPrandtl-Reussの
成分
![]() と直交していることになる。
したがって図-9.45に
示したように,
と直交していることになる。
したがって図-9.45に
示したように,
![]() は
降伏曲面の接線方向成分になっていることがわかる。
は
降伏曲面の接線方向成分になっていることがわかる。
加えた項は偏差成分しか持たないので,流れ則の式(9.146)に
式(9.130b)の塑性ポテンシャルを代入すると
となる。これを式(9.135)の整合条件に代入すれば![]() が
求められることになるが,ここで累積塑性ひずみの平方根の中を
算定すると
が
求められることになるが,ここで累積塑性ひずみの平方根の中を
算定すると
となる。これまでのモデルを見ればわかるように,
右辺(これまでの![]() )は
硬化係数
)は
硬化係数![]() の逆数のオーダーを持っているのに対し,ここで
新たに導入した
の逆数のオーダーを持っているのに対し,ここで
新たに導入した![]() は弾性係数と同じくらいのオーダーを
持つと考えられているのが普通である。したがって,
上式の
は弾性係数と同じくらいのオーダーを
持つと考えられているのが普通である。したがって,
上式の![]() に比べて第2項は非常に小さいと近似仮定できるので,
以下,無視することにする。以上の近似によって,式(9.136a)と同じく
に比べて第2項は非常に小さいと近似仮定できるので,
以下,無視することにする。以上の近似によって,式(9.136a)と同じく
と求められる。ここの硬化係数![]() も式(9.136b)で定義したものと
同じである。
これを流れ則の式(9.146)に代入することによって,
塑性ひずみ増分が
も式(9.136b)で定義したものと
同じである。
これを流れ則の式(9.146)に代入することによって,
塑性ひずみ増分が
と求められる。弾性成分は式(9.40)で与えられるので,
それと上式を
加算則の式(9.21)に代入すれば,総ひずみ増分が
となる。このモデルは, 後述の節-9.5.2 (5)で, 内部摩擦角を導入したすべり線理論とも比較される。
式(9.148)のひずみ増分を,偏差成分と体積変形成分に
分解した上で,前節の同様の成分と比較する[65]と
という上バー付きのパラメータを定義して,前節の上バー無しの
各パラメータをそれで置き換えさえすれば,前節の表現式で非共軸性を
考慮した増分関係を得ることができることがわかる。
ここに![]() は式(9.49)で定義したスィッチである。
つまり式(9.148)は
は式(9.49)で定義したスィッチである。
つまり式(9.148)は
と書くこともでき,したがってその逆関係は
となる。ただし, 弾塑性状態では,上バーの付いた材料パラメータに弾性と塑性の両方の成分が 含まれていることに注意する。 また整合条件を近似していることから,増分のみの数値解析においては 大きな変形になるにつれて降伏条件を満足しなくなる9.34ことには注意する。
元々非共軸項を考慮しようとしたのは,共軸材料がかなり安定な
材料特性を持っており,例えば塑性加工や砂等の要素試験で観察される
「しわ」や「絞り」「すべり線」「せん断帯」
等の不安定挙動を,
有限変形解析においてもうまく予測できなかったからであろう。
式(9.149)から明らかなように,例えば![]() によって
見かけ上の「弾性(接線)」せん断係数を小さくすることができ,
「せん断帯」等の発生が促進されることがある。
注意しなければならないのは,
によって
見かけ上の「弾性(接線)」せん断係数を小さくすることができ,
「せん断帯」等の発生が促進されることがある。
注意しなければならないのは,![]() を小さくとり過ぎると,見かけ上の
硬化
を小さくとり過ぎると,見かけ上の
硬化![]() が負(軟化)
になる可能性があるということである。
ただし,流れ則を解くときに仮定した近似のように,
が負(軟化)
になる可能性があるということである。
ただし,流れ則を解くときに仮定した近似のように,![]() を満たす
べきであることにも留意する必要がある。
この非共軸モデルは,降伏曲面に角点がある材料の簡易なモデルであると
書いたが,
を満たす
べきであることにも留意する必要がある。
この非共軸モデルは,降伏曲面に角点がある材料の簡易なモデルであると
書いたが,![]() が応力ひずみ関係曲線のいわゆる割線係数
に相当する全ひずみ理論
によって定式化されたモデルである[69]とも考えられている。
が応力ひずみ関係曲線のいわゆる割線係数
に相当する全ひずみ理論
によって定式化されたモデルである[69]とも考えられている。![]() が
応力ひずみ関係曲線の接線係数
に相当することに対応している。
が
応力ひずみ関係曲線の接線係数
に相当することに対応している。
さて,この章ここまでのほとんどでは,![]() 等の
硬化係数が定数であるような印象を与えてきたが,
一般には変形履歴に依存した非線形なパラメータである。
塑性加工のような大変形解析でよく用いられるモデルに,べき乗則
と呼ばれるモデルがある。
その一つは,平面応力状態の1軸引張り試験の応力ひずみ関係をモデル化したもので
等の
硬化係数が定数であるような印象を与えてきたが,
一般には変形履歴に依存した非線形なパラメータである。
塑性加工のような大変形解析でよく用いられるモデルに,べき乗則
と呼ばれるモデルがある。
その一つは,平面応力状態の1軸引張り試験の応力ひずみ関係をモデル化したもので
とする。![]() はYoung率で,
はYoung率で,![]() が塑性硬化についての
材料パラメータであり,例えば
が塑性硬化についての
材料パラメータであり,例えば![]() のような値を
設定する。
のような値を
設定する。
![]() は初期降伏時の
ひずみで
は初期降伏時の
ひずみで
![]() である。
ここでは弾性部分を無視し,このべき乗則によってモデル化される
硬化係数の表現を求めてみよう。
べき乗則は1軸引張り試験を念頭に置いていることから,
である。
ここでは弾性部分を無視し,このべき乗則によってモデル化される
硬化係数の表現を求めてみよう。
べき乗則は1軸引張り試験を念頭に置いていることから,![]() ,
,
![]() をそれぞれ式(9.28) (9.29)の
相当応力・相当塑性ひずみ
をそれぞれ式(9.28) (9.29)の
相当応力・相当塑性ひずみ
![]() ,
,
![]() に
関連させるのが望ましいだろう。
一方,
に
関連させるのが望ましいだろう。
一方,![]() や
や![]() は,式(9.22a)や式(9.26)で
定義されたせん断応力ノルム・累積塑性ひずみの間の
係数と考えるべきである。
この2種類の応力ノルム・塑性ひずみノルムの間の関係から
は,式(9.22a)や式(9.26)で
定義されたせん断応力ノルム・累積塑性ひずみの間の
係数と考えるべきである。
この2種類の応力ノルム・塑性ひずみノルムの間の関係から
という関係がある。また
であることから
という関係がある。ここに![]() は
せん断弾性係数であり
は
せん断弾性係数であり![]() はPoisson比である。
はPoisson比である。
![]() は
初期降伏せん断ひずみと考えればいい。累積塑性ひずみは工学ひずみに
相当するから,
は
初期降伏せん断ひずみと考えればいい。累積塑性ひずみは工学ひずみに
相当するから,![]() ではなく
ではなく![]() で除して定義した。
そこで式(
で除して定義した。
そこで式(![]() )の
)の
![]() を
を![]() と置き,
一方式(
と置き,
一方式(![]() )の
)の
![]() を
を![]() と置いた上で,
式(9.152)の
と置いた上で,
式(9.152)の
![]() を
を
![]() で,
すなわち
で,
すなわち
![]() で置き換え,
で置き換え,
![]() を
を
![]() で,すなわち
で,すなわち
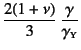 で置き換えれば,降伏後のべき乗則は
で置き換えれば,降伏後のべき乗則は
と書くことができる。したがって,平面応力状態の1軸引張りから
始めたために弾性係数がややおかしいものの,べき乗則は
と書くことができる。
さて,硬化係数は降伏後の応力ひずみ曲線の接線に相当するので
となる。同様に![]() が割線係数であると解釈できることから
が割線係数であると解釈できることから
と表すことができる。結局
| (9.154) |
となる。接線と割線で定式化したため,![]() が
が![]() よりも小さいという
適正なモデルになっていることもわかる。
よりも小さいという
適正なモデルになっていることもわかる。
ちなみに,随所に現れるPoisson比を含む係数は![]() の
場合には
の
場合には![]() という値を持つ。さらに,塑性変形が非圧縮性を
有することから,このべき乗則のPoisson比が弾塑性の見かけ上の
それであると解釈して極限として
という値を持つ。さらに,塑性変形が非圧縮性を
有することから,このべき乗則のPoisson比が弾塑性の見かけ上の
それであると解釈して極限として![]() と置くと,べき乗則は
と置くと,べき乗則は
と書くことができ,二つの硬化係数も
となる。これを用いれば,![]() を実験等からうまく同定することによって,
硬化後に非線形挙動を示す材料の簡単なモデルを作ることができる。
そのような数値解析では,上式の
を実験等からうまく同定することによって,
硬化後に非線形挙動を示す材料の簡単なモデルを作ることができる。
そのような数値解析では,上式の![]() は,
累積塑性ひずみ
は,
累積塑性ひずみ
![]() で置き換えればいいだろう。
あるいはもっと簡略に,2種類の塑性ひずみノルムの関係をそのまま
初期降伏ひずみにも当てはめて
で置き換えればいいだろう。
あるいはもっと簡略に,2種類の塑性ひずみノルムの関係をそのまま
初期降伏ひずみにも当てはめて
![]() とすると,式(9.152)は
とすると,式(9.152)は
| (9.157) |
となると考えてもいいかもしれない。
もう一つのべき乗則に,改訂Ludwik式[71,78]というものがあり,
それは降伏関数を
で定義している。引張り試験を元にしているため,
式(9.28) (9.29)の相当応力と
相当塑性ひずみを用いてある。これをせん断で定義した降伏関数に
変換すると
になる。これに対応する硬化係数はその定義式(9.62b)から
となる。いくつかの例を図-9.46に示した。
ここまでは等方性を持つ降伏条件を列挙してきたが,文献[34]の
直交異方性を一般化した文献[92]の詳細な解説を,
簡単に説明しておく。Trescaの降伏条件でも説明したように,
また![]() の表現式(9.51)からもわかるように,
直応力の差がせん断応力に密接に関係していることから,降伏関数には
の表現式(9.51)からもわかるように,
直応力の差がせん断応力に密接に関係していることから,降伏関数には![]() の
代わりに
の
代わりに
を用いればいい。ここで1行目がHillの直交異方性の場合の
成分である。さらに
の場合が,等方材料のMisesの降伏条件に相当する。