�ŐV�ł𐳊m�ɓǂޏꍇ�ɂ� pdf �t�@�C�� ���ǂ����B����� web �����̂��߂̊ȈՋ��łł��B
�O�߂ŊT������1�����ɂ�����Y���̍l������3�����Ɋg������B
�����ł͂܂��C
���ݍł���{�I�ȃ��f���Ƃ��Ĉ����C��ɍ|���̓����ώ���
�����������ޗ��ɑ��ėp�����Ă���Prandtl-Reuss�̃��f����
�\�z���������B
�܂��^���w��̐ݒ�Ƃ��āC��(9.4)�Ɠ��l�C
�Ђ��ݑ��������̒e�������ƑY�������ɕ����������̂Ƃ���B
�܂�C
![]() ���Ђ��ݑ�����
�Y�������Ƃ��C�e��������
���Ђ��ݑ�����
�Y�������Ƃ��C�e��������
![]() �ƋL�����Ƃ��ɁC
���Ђ��ݑ�����
�ƋL�����Ƃ��ɁC
���Ђ��ݑ�����
�̂悤�ɕ��������B�Ȃ��C��t���̃h�b�g�͑�����\���Ă���C
�����܂ŗp���Ă���![]() ���邢�͔���
���邢�͔���![]() �̑���ł���C
�ȉ����̏�t���h�b�g�ő�����\�����Ƃɂ���B
�̑���ł���C
�ȉ����̏�t���h�b�g�ő�����\�����Ƃɂ���B![]() �͑��x��
�����Ă��������C���̏͂̑Y���_�ł́u���ԁv��
�u�ό`�i���́j�����v�ł�����ۂ̎��Ԃł͂Ȃ���
���Ԃ̒P�ʂ�L���Ȃ���������9.8�Ȃ̂ŁC
�͑��x��
�����Ă��������C���̏͂̑Y���_�ł́u���ԁv��
�u�ό`�i���́j�����v�ł�����ۂ̎��Ԃł͂Ȃ���
���Ԃ̒P�ʂ�L���Ȃ���������9.8�Ȃ̂ŁC![]() ��
���ۂɂ͕ψʑ����ł���B�܂�C���̏͂ł�
��
���ۂɂ͕ψʑ����ł���B�܂�C���̏͂ł�
�̂悤�ɁC���x�Ƒ����ƑS���������ׂ�������\���L���Ƃ��ėp����B �㎮(9.21)���疾�炩�Ȃ悤�ɁC ���Ђ��ݑ����͎�(3.16)���Ђ��݂� �\�����K������������K���Ђ��݂ł��邪�C �����e�������ƑY�������͋��Ɂu��K���Ђ��݁v �ł�������9.9�ɂ͒��ӂ���B �܂����̊W���͔����ό`�̘g�g�ł͑S�����͖����ƍl���Ă������C ��ό`�̘g�g�̒��ł��C�ό`���z�̏�Z���� �ډׂ̏u�Ԗ��Ɂu����Q�Ə�ԁv�ɂ����đ������Ƃ������̂ł���C �m������[58]/�ߎ��I��[93]�n����9.10������̂ŁC �{���I�ɂ͕ό`���z�̏�Z���Ɛ�������l�����ł���B �ڍׂ͐�-12.2.2, 12.2.3�� �Q�Ƃ̂��ƁB
���đO�߂̎����ώ@�̍��ŏq�ׂ��悤�ɁC�|�̂悤�ȍޗ��̏ꍇ��
��ʂɐÐ����ł͑Y���ό`�͂قƂ�ǔ������Ȃ��B
���������āC�Y���ό`�������x�z���Ă���̂́C����f�ό`�����
����f��R����ł���ƍl����̂��K�ł���B
�������C��(9.16)�O��ʼn�������悤�ɁC
�c���ό`�͕ό`�����ɏ]���ėݐς��邱�Ƃ���C�~���������C
���̗ݐς���ό`���邢�͂Ђ��݂ŋK�肷�邱�Ƃ�
�K�ł͂Ȃ����낤�B���̂悤�ɍl����ƁC
����f��R�������\���Ă��鉞�͐����C
���Ȃ킿�C��(3.39)�Œ�`����
�����͂ō~��������^��������K�ł��낤�B
�������C������W�n�ł̕����̓e���\���́u�����v��
���̏�����^���邱�Ƃ́C�͊w�I�ɂ͂܂����Ƃ������Ƃ͖��炩���B
�Ƃ����̂��C�ޗ��̐����́C������ώ@���邢�͋L�q���Ă���l�Ԃ̓s����
�����������W�n�ɂ͈ˑ����Ȃ�
�͂�9.11������ł���B
���������āC���W�Ƃ͊W�̖����ʂƂ��āC�����͂̎�l�i������́j��
�s�ϗʂ�p����̂��K�ł��낤�B
�����͎�(3.39)��
��1�s�ϗʁi![]() �ƋL�����Ƃɂ���j�́C��(3.35)�̉��͂�
�s�ϗʂɏ����ĎZ�肷���
��
�ƋL�����Ƃɂ���j�́C��(3.35)�̉��͂�
�s�ϗʂɏ����ĎZ�肷���
��
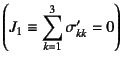 ��
�Ȃ邪�C����ȊO�̑�2, 3�s�ϗʂ�
��
�Ȃ邪�C����ȊO�̑�2, 3�s�ϗʂ�
(9.22)
�ƒ�`�ł���B����![]() �̒�`��
��(3.35b)�Œ�`�������͂̑�2�s�ϗ�
�̒�`��
��(3.35b)�Œ�`�������͂̑�2�s�ϗ�![]() �Ƃł�
�������قȂ��Ă���̂Œ��ӂ���B
�܂�������͂�
�Ƃł�
�������قȂ��Ă���̂Œ��ӂ���B
�܂�������͂�![]() �ƒu���ƁC��������߂鎮��
�ƒu���ƁC��������߂鎮��
�ƂȂ�B3���������̍��̌�������C�������
��
�Ƌ��߂���B������![]() �́C
��q�̎�(9.55)��Lode�p�Ƃ��W���邪
�́C
��q�̎�(9.55)��Lode�p�Ƃ��W���邪
������p�ł���B�������
![]() �ł���B
�����p����Ǝ��̂悤�ȍ~���������l������B
�ł���B
�����p����Ǝ��̂悤�ȍ~���������l������B
�����ł͂܂��C��҂̑�2�s�ϗʂ�����p���邻��Mises�̃��f����������悤�B
�x�N�g���̃m�����̊g���Ƃ��ĉ��߂���ƁC
![]() ��
�����͂̈��̃m�����ƍl���Ă��悳�������B
���ʂȗ�Ƃ��āC
��
�����͂̈��̃m�����ƍl���Ă��悳�������B
���ʂȗ�Ƃ��āC![]() -
-![]() �ʓ��̒P���Ȃ���f���͏�Ԃ�
����ꍇ���l����ƁC���̓e���\��������
�ʓ��̒P���Ȃ���f���͏�Ԃ�
����ꍇ���l����ƁC���̓e���\��������![]() �݂̂����Ȃ̂ŁC
������㎮�ɑ�������
�݂̂����Ȃ̂ŁC
������㎮�ɑ�������
![]() �ƂȂ�B
���̂��Ƃ�����C
�ƂȂ�B
���̂��Ƃ�����C
![]() ��
����f��R���\�����w�W�ł��邱�Ƃ��킩��B
�Ȃ����̕����ł́C���ƂŒ�`����
��
����f��R���\�����w�W�ł��邱�Ƃ��킩��B
�Ȃ����̕����ł́C���ƂŒ�`����
![]() �̖��̂Ɠ������C
��������u�������́v
�ƌĂԂ��Ƃ�����̂Œ��ӂ��ė~�����B
����
�̖��̂Ɠ������C
��������u�������́v
�ƌĂԂ��Ƃ�����̂Œ��ӂ��ė~�����B
����
![]() ������
���E�l�ɒB�����Ƃ��ɑY���ό`����������ƍl�����
������
���E�l�ɒB�����Ƃ��ɑY���ό`����������ƍl�����
���~������
�ɂȂ�B�e����Ԃ�![]() �Œ�`����C
�Œ�`����C![]() �̏�Ԃ͋��e����Ȃ��B
���̍~��������Mises�̍~������
�Ƃ��Ă�Ă���B
����
�̏�Ԃ͋��e����Ȃ��B
���̍~��������Mises�̍~������
�Ƃ��Ă�Ă���B
����![]() ���~����
�ł���C
���~����
�ł���C![]() ������f�~������
�ł���B
������f�~������
�ł���B
![]() �́C�Y���ό`�������Ɉˑ����邱�Ƃ�
�z�ɕ\�����߂ɒ�`���ꂽ�X�J���[�ʂł���C��q�̂悤��
�Y���d�������̕����I�Ӗ����l������ƁC
�������͂̒�`��(9.22a)�ɑΉ�������
�́C�Y���ό`�������Ɉˑ����邱�Ƃ�
�z�ɕ\�����߂ɒ�`���ꂽ�X�J���[�ʂł���C��q�̂悤��
�Y���d�������̕����I�Ӗ����l������ƁC
�������͂̒�`��(9.22a)�ɑΉ�������
�Œ�`��������B�O�q�̂悤��![]() �͎��Ԃł͂Ȃ��C
������\���������̒P�������p�����[�^�ł���B
������ݐϑY���Ђ���
�i�܂�Y���Ђ��ݑ����̑�2�s�ϗ�9.12�����ʂ̗ݐ�9.13�j�ƌĂԂ��Ƃɂ���B
�������ȉ��ł́C��q��
�͎��Ԃł͂Ȃ��C
������\���������̒P�������p�����[�^�ł���B
������ݐϑY���Ђ���
�i�܂�Y���Ђ��ݑ����̑�2�s�ϗ�9.12�����ʂ̗ݐ�9.13�j�ƌĂԂ��Ƃɂ���B
�������ȉ��ł́C��q��
![]() �Ɠ��l�C
���̗ݐϑY���Ђ��݂��u�����Y���Ђ��݁v
�ƌĂԂ��Ƃ�����̂Œ��ӂ��ė~�����B
��`���ɗp�����ϕ��́C�����ɉ����ė݉������邱�Ƃ�\���Ă���B
�Ȃ��C���̗ݐϑY���Ђ��݂͂Ђ��݃e���\���̂���f������2�{�C
�܂肢�����H�w�Ђ���
�ɑ������Ă���i�O��1�����̏ꍇ��
�Ɠ��l�C
���̗ݐϑY���Ђ��݂��u�����Y���Ђ��݁v
�ƌĂԂ��Ƃ�����̂Œ��ӂ��ė~�����B
��`���ɗp�����ϕ��́C�����ɉ����ė݉������邱�Ƃ�\���Ă���B
�Ȃ��C���̗ݐϑY���Ђ��݂͂Ђ��݃e���\���̂���f������2�{�C
�܂肢�����H�w�Ђ���
�ɑ������Ă���i�O��1�����̏ꍇ��![]() �j���Ƃɒ��ӂ���B
�d���ɔ����č~�����͂�
�ω����邱�Ƃ��������߂�
�j���Ƃɒ��ӂ���B
�d���ɔ����č~�����͂�
�ω����邱�Ƃ��������߂�![]() ��
�ݐϑY���Ђ��݂̊��ŗ^�����̂ł���B
��
�ݐϑY���Ђ��݂̊��ŗ^�����̂ł���B
����C�|��1�������莎���̂悤�ɁC�Ⴆ��![]() ������
����
������
����![]() ���������ł���悤�ȏꍇ�ɂ́C
��(9.22a)��
���������ł���悤�ȏꍇ�ɂ́C
��(9.22a)��
![]() ��
�Ȃ�̂ŁC�~��������
��
�Ȃ�̂ŁC�~��������
![]() �ƂȂ�B
���̂��Ƃ���C������~��
����
�ƂȂ�B
���̂��Ƃ���C������~��
����
![]() �Ƃ���f�~�����͂�
�Ƃ���f�~�����͂�
�Ƃ����W�ɂ���9.14���Ƃ��킩��B
���̂��߁C��(9.22a) (9.25)�̑����
�̂悤�ɍ~�������`���Ă���ꍇ������B
����
![]() ����������
�ƌĂ�9.15�Ă���B
�\����͂ɂ�����~���̑�\�l�Ƃ��ẮC���̈�����~�����͂̕���
�悭�p������B���̒�`��p����ꍇ�ɂ́C
��q�̎�(9.34)�Ɏ����Y���d��������
�����I�Ӗ�����C��(9.26)�̗ݐϑY���Ђ��݂�
����������
�ƌĂ�9.15�Ă���B
�\����͂ɂ�����~���̑�\�l�Ƃ��ẮC���̈�����~�����͂̕���
�悭�p������B���̒�`��p����ꍇ�ɂ́C
��q�̎�(9.34)�Ɏ����Y���d��������
�����I�Ӗ�����C��(9.26)�̗ݐϑY���Ђ��݂�
�ƒ�`�������Ă������������B����������Y���Ђ���
�ƌĂ�ł���B�萔![]() �����̈Ⴂ�����琔�l�I�Ȃ��Ƃ͖��ɂ͂Ȃ�Ȃ����C
���̕����ł́C�~�����������ׂ�܂肹��f�Ɏ��
�ւ���Ă��邱�Ƃ���C
�����̈Ⴂ�����琔�l�I�Ȃ��Ƃ͖��ɂ͂Ȃ�Ȃ����C
���̕����ł́C�~�����������ׂ�܂肹��f�Ɏ��
�ւ���Ă��邱�Ƃ���C
![]() ��
��
![]() ��
������ɗp����B
��
������ɗp����B
���̂悤�ɁC �Y���ό`����ɂ���f�Ŏx�z����Ă��邱�Ƃ�����ސ��ł���悤�ɁC �~���������������ꂽ���Ƃ̑Y���ό`�́C ���̓����̔�t�I�Ȃ��ׂ�ό`�Ń��f�����ł��������B �܂�C�}-9.15�ɖ͎��I�� �������悤�ɁC�O�͂̍�p�ɂ���� ���̓����ɐ��������͐����̑g�ݍ��킹���C ���������������������ʏ�9.16�ł� ���C��R�͂ɂ��C���ׂ�̔���9.17���\�ɂȂ�̂ł���B ���̂悤�ɁC����ʏ�̉��͏�Ԃ����ׂ�� �\�ɂ����ꍇ�Ɂu�~���������������ꂽ�v�Ɣ��f�ł��C �����ɑY���ό`��������ƍl����̂ł���B ���������āC��-9.1.3�̖��C�Ƃ��ׂ�� ���������悤�ɁC���̂��Ƃ̂��ׂ�ό`�̌����͂��̖ʂ̌����C �܂����͐����̑g�ݍ��킹�̌����Ō��܂��Ă��܂��B ����͒e���ό`�ɂ͖��������ł���B
�ʐS�������������ɂƂ��āC���̔����I�ȃ��J�j�Y���̊ȒP�ȃ��f����
��������ƈȉ��̂悤�ɂȂ�B�}-9.16�̍���
�����\����͂������̂ł��邪�C���̌��q�z�u�̍ł��f���Ȗʂ�
���ׂ�Ղ��i�]�ʂ��ړ����Ղ��j�Ƃ���Ă���B
���̂��ׂ�ʂ��E�}�Ɏ������B�O�p�`ABC�̖ʂ��悭(111)�ʂ�
�Ă����̂ŁC���̓����ȖʎO��Ԋ|���ŋ�ʂ��Ď������B
���̎l�̖ʂŐ��l�ʑ̂��`�����Ă���B
�����āC���ׂ�����͖���3����AB, BC, CA�Ɂi���̕������\�j�Ȃ�B
���v��4��![]() 3�����C�܂�12�ʂ�i���̕�������ʂ����24�ʂ�j��
���ׂ肪�\�Ȕ����\���ɂȂ��Ă���B�t�ɁC���̖ʂ̌����̂��̕�����
���ׂ肵���\�ɂ͂Ȃ�Ȃ��\���ɂȂ��Ă���ƍl����̂ł���B
�����Ă��̂����̈�ȏ�̂��ׂ�ʏ�ŁC
�Ⴆ�Ύ�(9.25)�����鉞�͏�ԂɂȂ����Ƃ��ɍ~����������������C
���ׂ�i�]�ʂ������j�\��9.18��
��������ƍl����̂ł���B
3�����C�܂�12�ʂ�i���̕�������ʂ����24�ʂ�j��
���ׂ肪�\�Ȕ����\���ɂȂ��Ă���B�t�ɁC���̖ʂ̌����̂��̕�����
���ׂ肵���\�ɂ͂Ȃ�Ȃ��\���ɂȂ��Ă���ƍl����̂ł���B
�����Ă��̂����̈�ȏ�̂��ׂ�ʏ�ŁC
�Ⴆ�Ύ�(9.25)�����鉞�͏�ԂɂȂ����Ƃ��ɍ~����������������C
���ׂ�i�]�ʂ������j�\��9.18��
��������ƍl����̂ł���B
�~���������������Ƃ̒�R�����́C�O�߂ł��q�ׂ��悤�Ɉ�Έ�� �����������Ȃ����Ƃ������āC �Ђ��ݑ��������͓��ƂȂ�炩�̊W�ɂ���Ƃ������ꗝ�_ �ŗ^����K�v������B���������Ē�R�����́C ���͑��x�i�����j�ƂЂ��ݑ��x�i�����j���W�t�����������_ �ɂȂ�B ���̂悤�ɁC���݂̏�Ԃ���ǂ̂悤�ɔ��W����̂��C �܂葝����ω����ǂ̂悤�ɐ�����̂��L�q�������̂����ꑥ ���邢�����W�� �Ƒ��̂��Ă���B
���ꑥ�̋L�q��Hill�̕���[34]���炻�̂܂܈��p�����
�܂�Saint-Venant��1870�N��
�Ɠ��@���CLèvy (1871)��Mises (1913)�����l��
�ɂȂ�Ƃ����B���̌�Prandtl (1924)��Reuss (1930)�́C �e���ƑY�������čl����K�v������Ƃ���
�ł���Ƃ����iPrandtl-Reuss�̎��j�B
�̂悤�ɂȂ�B
�܂�i�v�ό`�̕ω�
![]() ��
������
��
������![]() �Ɠ��������ɔ������悤�Ƃ���B
�����͂������I�ɂ͂���f���͂ł��邱�Ƃ��v���o���ƁC
���̗��ꑥ�̎�(9.30)��
���C�Ƃ��ׂ�Ő���������(9.15)��
�����ŁC�i�v�ό`�͂���f�ό`�ł��邱�Ƃ��킩��B
�܂���(9.30)�͂�����S���̋L�q�ɂ悭���Ă��邪�C
�S���Ƃ͈قȂ�C�E�ӂ�
�Ɠ��������ɔ������悤�Ƃ���B
�����͂������I�ɂ͂���f���͂ł��邱�Ƃ��v���o���ƁC
���̗��ꑥ�̎�(9.30)��
���C�Ƃ��ׂ�Ő���������(9.15)��
�����ŁC�i�v�ό`�͂���f�ό`�ł��邱�Ƃ��킩��B
�܂���(9.30)�͂�����S���̋L�q�ɂ悭���Ă��邪�C
�S���Ƃ͈قȂ�C�E�ӂ�
![]() �͉��͏�ԂƉ��͑�����
�ˑ��������p�����[�^�ł���C�P���ȍޗ��p�����[�^�ł͂Ȃ��B
��̓I�Ɏ�(9.30)����(9.26)��
�������(9.22a)���l�������
�͉��͏�ԂƉ��͑�����
�ˑ��������p�����[�^�ł���C�P���ȍޗ��p�����[�^�ł͂Ȃ��B
��̓I�Ɏ�(9.30)����(9.26)��
�������(9.22a)���l�������
�ƂȂ�C
![]() �����͂ƑY���Ђ��ݑ�����
�ˑ����Ă��邱�Ƃ��킩��B
�܂��C���ꂪ
�����͂ƑY���Ђ��ݑ�����
�ˑ����Ă��邱�Ƃ��킩��B
�܂��C���ꂪ
![]() �̕����I�ȈӖ��ł���B
�̕����I�ȈӖ��ł���B
���̎�(9.30)������C
�Y�����e���Ɩ{���I�ɈقȂ��Ă��邱�Ƃ����炩�ł���B
���Ȃ킿�C�Y���̏ꍇ�ɂ�Saint-Venant���L�q�����悤�ɁC
�u�Y���Ђ������������i����f�j�������̂��̂�������
���낤�Ƃ���v
�̂ɑ��i�������j
�C�e���̏ꍇ�ɂ͎�(3.40) (3.41)���疾�炩�Ȃ悤�ɁC
�u�e���Ђ��݂͉��͂ƁC�܂�
�e���Ђ������������������������ł��낤�Ƃ���v
���ƂɂȂ�B
�����ɁC
![]() ,
,
![]() �͂��ꂼ��
��(3.14)�Œ�`�����̐ςЂ��݂�
�e�������ƑY�������ł���C
�͂��ꂼ��
��(3.14)�Œ�`�����̐ςЂ��݂�
�e�������ƑY�������ł���C![]() ��
��(3.38)�Œ�`���ꂽ���ω��͂ł���B
����������ƁC�ό`�̑����ɒ��ڂ����Ƃ��ɁC
�u�e���ł͂��̑����ό`�̌������傫�������͑����ɒ��ڊW���Ă���v���C
�u�Y���ł́C�����ό`�������͉��͂��̂��̂̌����Ɏx�z����邪�C
���̑����ό`���傫���ɂ͉��͑������e����^����v���ƂɂȂ�B
����́C���̂悤�ȑY���́u�������J�j�Y���v���l����ƁC
�����͂킩��Ղ���������Ȃ��B
��
��(3.38)�Œ�`���ꂽ���ω��͂ł���B
����������ƁC�ό`�̑����ɒ��ڂ����Ƃ��ɁC
�u�e���ł͂��̑����ό`�̌������傫�������͑����ɒ��ڊW���Ă���v���C
�u�Y���ł́C�����ό`�������͉��͂��̂��̂̌����Ɏx�z����邪�C
���̑����ό`���傫���ɂ͉��͑������e����^����v���ƂɂȂ�B
����́C���̂悤�ȑY���́u�������J�j�Y���v���l����ƁC
�����͂킩��Ղ���������Ȃ��B
�܂�C�}-9.15��p���Đ��������悤�ɁC ����ʏ�Łu�~�������v���������ꂽ�ꍇ�C ���̖ʂ̌����ł��̂��Ƃ̑Y���ό`�̌����͊��Ɍ��肳��Ă��܂��Ă���B ���������āC���̌コ��ɊO�͂𑝂₻���Ƃ����ꍇ�C ���̂��ׂ�ʏ�ł̂��ׂ�ό`����9.19�����悤�Ƃ͂��Ȃ����낤�B ���̂��Ƃ���C���̑����ό`�̌����� ���ׂ�o�����Ƃ��邷�ׂ�ʂ̌����Ō��肳��C���ǁC �����ό`�̌����͉��͏�Ԃ��̂��̂Ŏx�z����邱�ƂɂȂ�B ����C�}-9.17�̂悤�ɁC ���ۂɂ��ׂ�ό`�i�����j�������邩�ǂ����́C �����ɔ������鉞�͑����̌����Ƒ傫���Ɉˑ�����B ���̌��ۂ��L�q����̂��u���ꑥ�v�̕����ł���B
���Ă����ŁC�Y���d������
��p���ď�q�̋������ɂ��čl�@���Ă������B
�Y���d���������C���鉞�͏�ԂŁC���̉��͂��Y���Ђ��ݑ����Ƃ���d����
�ƒ�`����B���ꑥ�̎�(9.30)��
��(9.33)�ɑ������ƁC
��(9.22a)��
![]() ���邢��
��(9.28)��
���邢��
��(9.28)��
![]() ��p����
��p����
�Ƃ����W����������B�����ŁC��(9.26)��
�ݐϑY���Ђ���
![]() ���邢��
��(9.29)�̑����Y���Ђ���
���邢��
��(9.29)�̑����Y���Ђ���
![]() �́C
���ꂼ��̑����Ɏ�(9.30)�̗��ꑥ���������
�́C
���ꂼ��̑����Ɏ�(9.30)�̗��ꑥ���������
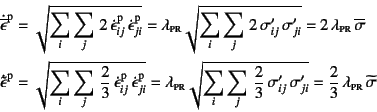
�ƂȂ�B���̎����狁�߂���
![]() ���㎮�ɑ�������
���㎮�ɑ�������
�Ƃ����W��B���ꂪ������ ����������ꍇ�̑厖�ȓ����ł���B
��(9.22a)��
![]() ������f���͂ɑ������C
��(9.28)��
������f���͂ɑ������C
��(9.28)��
![]() ���P�����͂�
�������Ă��邱�Ƃ�O���ɒu���C��̑Y���d�������̕\������C
��(9.26)��
�ݐϑY���Ђ���
���P�����͂�
�������Ă��邱�Ƃ�O���ɒu���C��̑Y���d�������̕\������C
��(9.26)��
�ݐϑY���Ђ���
![]() ��
��(9.29)�̑����Y���Ђ���
��
��(9.29)�̑����Y���Ђ���
![]() ��
�����I�ȈӖ��͖��炩�ł��낤�B�����ł́C���������z�Ȍ`�ł��̈Ӗ���
���炩�ɂ��Ă����B
�Ⴆ�ΑY���ό`��������f��Ԃɂ�����
��
�����I�ȈӖ��͖��炩�ł��낤�B�����ł́C���������z�Ȍ`�ł��̈Ӗ���
���炩�ɂ��Ă����B
�Ⴆ�ΑY���ό`��������f��Ԃɂ�����
![]() �ȊO�̐�����
��ł���C��(9.26)��
�ݐϑY���Ђ��ݑ���
�ȊO�̐�����
��ł���C��(9.26)��
�ݐϑY���Ђ��ݑ���
![]() ��
��
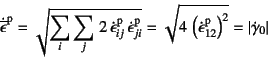
�ƂȂ�B���������đO�q�̂悤�ɁC�ݐϑY���Ђ��݂�
����f�H�w�Ђ��݂ɑ������邱�Ƃ��킩��B
�܂��C�P�����͏��
![]() �ō~�����Ă���ꍇ�ɂ́C
��(9.30)�̗��ꑥ����C�Ⴆ��
�ō~�����Ă���ꍇ�ɂ́C
��(9.30)�̗��ꑥ����C�Ⴆ��
�ƍl�����������C
��(9.29)�̑����Y���Ђ���
����
![]() ��
��
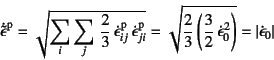
�ƂȂ�B ���������āC�����Y���Ђ��݂͒P���̐L�яk�݂Ђ��݂ɑ������邱�Ƃ��킩��B
�Y���ό`�́C��ɍ~��������������������ꍇ��
�������Ă���̂ŁC���̂悤�ȕό`���p������Ԃ�![]() ��
���葱���Ȃ���Ȃ�Ȃ��B
����������ƁC
��
���葱���Ȃ���Ȃ�Ȃ��B
����������ƁC![]() �͑Y���ό`���𒆂ɂ͕ω����Ȃ��̂ŁC���̕ω�������
�͑Y���ό`���𒆂ɂ͕ω����Ȃ��̂ŁC���̕ω�������
�����Ȃ���Ȃ�Ȃ��B���̏�������������
�ƌĂ�ł���B���̎��ɁC�~�����̋�̓I�Ȏ�(9.25)��
�������ƁC�S�������Ƃ�̂Ɠ�������ɂ����
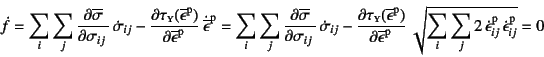
�ƂȂ�B�Ōォ���Ԗڂ̎��̑�2���̕������̒���
��(9.30)��
���ꑥ�������C��(9.22a)����
�ł��邱�Ƃ��l�����ď㎮�������
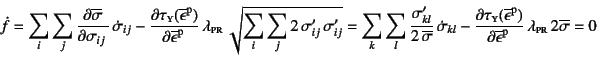
�ƂȂ邱�Ƃ���C
![]() ��
��
(9.37)
�Ƌ��߂���B������![]() ���d���W��
�ł���B�����
��(9.30)�̗��ꑥ�ɑ������C�Y���Ђ��ݑ�����
���d���W��
�ł���B�����
��(9.30)�̗��ꑥ�ɑ������C�Y���Ђ��ݑ�����
�Ƌ��߂���B�`�̏�ł́C1�����̏ꍇ�̎�(9.13)�Ƃ悭
�������Ă��邱�Ƃ��킩��B
���R�̂��Ƃ����C�Y���ό`�͂���f��������ł���Ƃ����̂ŁC�Y���I�ȑ̐ϕό`��
��
![]() �ɂȂ��Ă���B
���������āC�Y���ό`���k��
��L���Ă���9.20���ƂɂȂ�C���������Ӗ��ł́u��9.21�v��
�ό`�Ɠ����ł���B
�ɂȂ��Ă���B
���������āC�Y���ό`���k��
��L���Ă���9.20���ƂɂȂ�C���������Ӗ��ł́u��9.21�v��
�ό`�Ɠ����ł���B
�ȏ�̌��ʂ�p���đO�߂́u�ډׁv�u���ׁv���`���������B1�����̏ꍇ�ɂ�
�P���ɉ��͑�����
![]() �̐������邢�͗�̂������
�������邩�ŁC�ډׂƏ��ׂ̓�̏�Ԃ���ʂł����B3������
�ꍇ�͎�(9.37a)��
�̐������邢�͗�̂������
�������邩�ŁC�ډׂƏ��ׂ̓�̏�Ԃ���ʂł����B3������
�ꍇ�͎�(9.37a)��
![]() ���ډ����ł���C
��������Ȃ�
���ډ����ł���C
��������Ȃ�![]() �̏ꍇ�ɂ́C
�̏ꍇ�ɂ́C
![]() ���ډ����ɂȂ�B����������
���ډ����ɂȂ�B����������
�ƒ�`��������B�����������ډ�
�Ƃ́C�V���ȑY���Ђ��݂͔������Ȃ��܂܁C�~������������
�قȂ鉞�͏�Ԃɕω����邱�Ƃ��Ӗ����Ă���B
���̕����̓e���\���Ɖ��͑����e���\��9.22��
�ς̘a�����ł������
![]() �͈��̓��ς̐��l���Ȃ̂ŁC�w�I�ɉ��߂����
�u�ډׂ͕����́i����f���́j��
���͑����̌�����90�x�ȓ��i�قړ��������j�ɂ���v���Ƃ�
�Ӗ����Ă���C1�����̍ډ�Ԃ̒�`�̒P���Ȋg���ɂȂ��Ă��邱�Ƃ��킩��B
�͈��̓��ς̐��l���Ȃ̂ŁC�w�I�ɉ��߂����
�u�ډׂ͕����́i����f���́j��
���͑����̌�����90�x�ȓ��i�قړ��������j�ɂ���v���Ƃ�
�Ӗ����Ă���C1�����̍ډ�Ԃ̒�`�̒P���Ȋg���ɂȂ��Ă��邱�Ƃ��킩��B
����C�e��������Hooke�̖@���̎�(3.55)��
�������m�̊W�Ɋg��������(3.87)��
�^��������̂Ƃ���������낤�B�܂�
�Ƃ���B�������悤�ł��邪�C���̒e�������́C
���ӂ̂���f����������ƁC
![]() ��
�E�ӂ�
��
�E�ӂ�
![]() �������Y����
�������Y����![]() �������Ă��邱�Ƃ���C
���ꓯ�m�����������������Ă��邱�Ƃ��킩��B����ɑ���
��(9.38)���疾�炩�Ȃ悤�ɁC
�������Ă��邱�Ƃ���C
���ꓯ�m�����������������Ă��邱�Ƃ��킩��B����ɑ���
��(9.38)���疾�炩�Ȃ悤�ɁC
![]() ��
���͑���
��
���͑���
![]() �ł͂Ȃ�������
�ł͂Ȃ�������![]() ��
�����Y����
��
�����Y����![]() ����������B
�܂�C�Y���Ђ��ݑ����͉��͑����ł͂Ȃ�
���͂��̂��̂Ɠ��������������Ă���̂ł���B
�ŏI�I�ɁC���̓�̐����̎�(9.38)
(9.40)���C���Ђ��ݑ����̎�(9.21)��
��������
����������B
�܂�C�Y���Ђ��ݑ����͉��͑����ł͂Ȃ�
���͂��̂��̂Ɠ��������������Ă���̂ł���B
�ŏI�I�ɁC���̓�̐����̎�(9.38)
(9.40)���C���Ђ��ݑ����̎�(9.21)��
��������
�ƂȂ�B
���āC�Y���_�͂ǂ����đ����ʂŕ\����Ă���̂��Ƃ���������Ƃ��ǂ������B
��̕ό`��ԂōډׂƏ��ׂ̉\�������邱�Ƃ���̗��R���Ǝv�����C
���ꑥ���ϕ��\�ł͂Ȃ����Ƃ��ł��d�v�ȗ��R�ł��낤�B
�܂�㎮(9.38)�͈�ʂɂ͐ϕ��\�ł͂Ȃ��B���ꑥ�́C
���x���i�����j�ɒu���������ꍇ
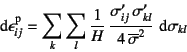
�Ɖ��߂ł��C�Ⴆ��
![]() ���ɂƂ��ēW�J��
���ɂƂ��ēW�J��
�Ə������Ƃ��ɁC������Ɩʓ|�Ȍv�Z���K�v�ɂȂ邪�C�ŏI�I�ɗႦ��
�ƂȂ��Ă��邱�Ƃ��킩��B
�܂�㎮(![]() )�͑S�����`���ɂ͂Ȃ��Ă��Ȃ����Ƃ���C�ϕ��ł��Ȃ��B
��̗���-9.3.3�Ɏ������B
�����I�Ɍ����C��������Y���Ђ��݂͍ډח����Ɉˑ����Č��ʂ��قȂ邱�ƂɂȂ�C
�Ⴆ���铯�����͏�ԂɎ���܂ł̍ډׂ̏�����ʂ��Ⴄ�ƁC
�������鑍�ό`�͈قȂ��Ă���̂ł���B
�Ⴆ�i�s�\�����j�S���������E�̔z�u�����������̂ŁC
���]�ʂ��S�������ꏊ�ɂ����̍ޗ����������Ƃ��悤�B
��̍ޗ��́C
)�͑S�����`���ɂ͂Ȃ��Ă��Ȃ����Ƃ���C�ϕ��ł��Ȃ��B
��̗���-9.3.3�Ɏ������B
�����I�Ɍ����C��������Y���Ђ��݂͍ډח����Ɉˑ����Č��ʂ��قȂ邱�ƂɂȂ�C
�Ⴆ���铯�����͏�ԂɎ���܂ł̍ډׂ̏�����ʂ��Ⴄ�ƁC
�������鑍�ό`�͈قȂ��Ă���̂ł���B
�Ⴆ�i�s�\�����j�S���������E�̔z�u�����������̂ŁC
���]�ʂ��S�������ꏊ�ɂ����̍ޗ����������Ƃ��悤�B
��̍ޗ��́C![]() ��
��![]() ��
������̔��
��
������̔��
![]() �Ɏ���܂ōډׂ����Ƃ���B
���̂Ƃ����E�ɒB���Ă��܂���
�Ɏ���܂ōډׂ����Ƃ���B
���̂Ƃ����E�ɒB���Ă��܂���![]() �̓]�ʂ�
���O��`d
�̓]�ʂ�
���O��`d![]() '����`d
'����`d![]() '�̂悤�ɕt�����Ƃ���B
�����ł�����̍ޗ��́C�܂�
'�̂悤�ɕt�����Ƃ���B
�����ł�����̍ޗ��́C�܂�![]() ��
��![]() �ɂȂ�܂�
�ډׂ��C��������ɕۂ����܂�
�ɂȂ�܂�
�ډׂ��C��������ɕۂ����܂�![]() ��
��![]() ��
����悤�Ȏ������ł����Ƃ��悤�B���̂Ƃ��C�������̍ޗ���
������`d
��
����悤�Ȏ������ł����Ƃ��悤�B���̂Ƃ��C�������̍ޗ���
������`d![]() '����`d
'����`d![]() '�̓]�ʂ͂��ׂė��E�Ɏ��邾�낤���B
�܁C�����������Ƃ͖������낤�B
���������đY���ό`�������ɂ������ˑ�
��������̂ł���B��������f�����������ꑥ�Ȃ̂ŁC
����������ˑ��̃��f���ɂȂ��Ă���B
�܂��Y���Ђ��ݑ����͒�`�ł�����̂́C�Y���Ђ��݂��̂��̂͒�`�ł����C
���ǐ��l��͂ŏ��������������Z�������đY���Ђ��݂��Z��������Ȃ��B
�����Ď��ŕ\�������
'�̓]�ʂ͂��ׂė��E�Ɏ��邾�낤���B
�܁C�����������Ƃ͖������낤�B
���������đY���ό`�������ɂ������ˑ�
��������̂ł���B��������f�����������ꑥ�Ȃ̂ŁC
����������ˑ��̃��f���ɂȂ��Ă���B
�܂��Y���Ђ��ݑ����͒�`�ł�����̂́C�Y���Ђ��݂��̂��̂͒�`�ł����C
���ǐ��l��͂ŏ��������������Z�������đY���Ђ��݂��Z��������Ȃ��B
�����Ď��ŕ\�������
�Ƃ�������9.23�ɂȂ�C
���l�v�Z�ł����Y���Ђ��݂͒�`�ł��Ȃ��B
���������Ď�(9.21)�̑����
�Ƃ������ɂ���̂́C�ŏI��Ԃ����łЂ��݂����߂���Ƃ����\����
�Ȃ��Ă��܂��ĕs�K�ł��邵�C�ߎ����S�Ђ��ݗ��_
�ƌ������鋰�ꂪ����̂Œ��ӂ��K�v�ł���B
���߂�
![]() �Ƃł����L���ׂ����낤�B
�Ƃł����L���ׂ����낤�B
���āC�L���v�f�@���ւ�
���p�̂��Ƃ��l����ƁC
��(9.41)�̋t�W�����߂������֗���������Ȃ��B
�܂��C��(9.41)��![]() ��
��![]() ����v������1����3�܂Řa���Ƃ�9.24��
����v������1����3�܂Řa���Ƃ�9.24��
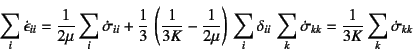
�ƂȂ邩��C���Ǖ��ω��͑�����

�ƂȂ�B�̐ϕω��ɂ͑Y���͊֗^���Ă��Ȃ�����C����͒e���W�݂̂�
�\�����B
���Ɏ�(9.41)��![]() ��
�悶��
��
�悶��![]() ��
��![]() ��1����3�܂Řa���Ƃ�C�d���������Z�肷���
��1����3�܂Řa���Ƃ�C�d���������Z�肷���
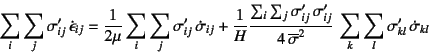
�ƂȂ�B
�E�ӑ�2���Ɏ�(9.22a)��
![]() �̒�`���l������ƁC
����
�̒�`���l������ƁC
����
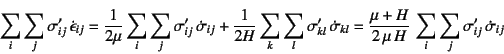
�ƂȂ邱�Ƃ���C�t�W�Ƃ���
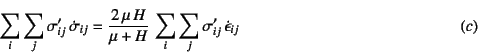
��B��(![]() ) (
) (![]() )����(9.41)��
�E�ӂɑ������C�E�ӑ�1���ȊO�͂��ׂĂЂ��ݑ����ŕ\�����B
����āC���ӂɂЂ��ݑ����̍����W�߂āC���E�����ւ��C
���ӂ�
)����(9.41)��
�E�ӂɑ������C�E�ӑ�1���ȊO�͂��ׂĂЂ��ݑ����ŕ\�����B
����āC���ӂɂЂ��ݑ����̍����W�߂āC���E�����ւ��C
���ӂ�![]() ���悶�邱�Ƃɂ����
���悶�邱�Ƃɂ����
��B��(3.43)��Lamé�̒萔��p����ƁC
���ǎ�(3.52)�̓����e���W��![]() ��p����
��p����
�Ƃ����������͑����Ђ��݊W
��B
�����ŁC
![]() ���}-9.8��
���}-9.8��![]() �C
�܂�e�����܂ތ�������̍d���W���ɑ�������B
�܂���(9.41)�̊W���C
��(3.54)�̒e���R���v���C�A���X��p����
�C
�܂�e�����܂ތ�������̍d���W���ɑ�������B
�܂���(9.41)�̊W���C
��(3.54)�̒e���R���v���C�A���X��p����
�ƕ\�����Ƃ��ł���B
���邢�́C�e�Y���ڐ��W��
������ڐ��R���v���C�A���X
��
�ƒ�`����C�����\����������
�ƕ\�����Ƃ��ł���B������![]() �͍ډׁE���ׂ���ʂ���X�B�b�`��
�͍ډׁE���ׂ���ʂ���X�B�b�`��
�ƒ�`�����B�ēx�������悤�ł��邪�C���̂悤�ɕ\�����Ă��܂��ƁC �e�Y���W���ƒe���W���������悤�Ɍ����Ă��܂����Ƃ���C �e���ƑY���̕����I�ȈႢ��Y��Ă��܂��\��������̂Œ��ӂ��邱�ƁB
���āC�d���W����![]() �͍ޗ�������\���p�����[�^�Ȃ̂ŁC
�ޗ��������Ō��肵�Ȃ���Ȃ�Ȃ��B��Ԋ�{�I�Ȏ�����1�������莎�����낤�B
�����Ŏ�(9.41)�́C1�����(
�͍ޗ�������\���p�����[�^�Ȃ̂ŁC
�ޗ��������Ō��肵�Ȃ���Ȃ�Ȃ��B��Ԋ�{�I�Ȏ�����1�������莎�����낤�B
�����Ŏ�(9.41)�́C1�����(
![]() ��
���̐����͂��ׂė�B���������l�B)�ł�
��
���̐����͂��ׂė�B���������l�B)�ł�
�Ƃ����W�ɂȂ�B������![]() ��Young���ł���C
��Young���ł���C![]() �͈����莎����
���͂Ђ��݊W�̐ڐ��W���ł���B���̊W���
�͈����莎����
���͂Ђ��݊W�̐ڐ��W���ł���B���̊W���
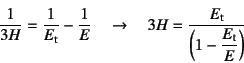
�ł��邱�Ƃ��킩��B
���邢�́C���͂ƑY���L�тЂ��݊W�̐ڐ��W����![]() �ł��邱�ƂɂȂ�B
����`3'�́C
�ł��邱�ƂɂȂ�B
����`3'�́C
![]() ��
��
![]() ����
��
����
��
![]() ��
��
![]() ��
�Ⴂ��
��
�Ⴂ��![]() ����h�����Ă���B
����h��������B
����C����f�������\�ł���C
![]() �݂̂�
��낾�Ƃ��ē��l�̌v�Z�������
�݂̂�
��낾�Ƃ��ē��l�̌v�Z�������
�ƂȂ�B![]() �͂���f�����̉��͂ƍH�w�Ђ��݂̊W�̐ڐ��W���ł���B
������
�͂���f�����̉��͂ƍH�w�Ђ��݂̊W�̐ڐ��W���ł���B
������
�ƂȂ�C �����1�������f���̏ꍇ�̍d���W���̎�(9.11b)�� �����W�������Ă���B �����œ��鉞���͈�ʂɂ͔���`����L���Ă��āC ������悭�u�ׂ��摥�v���ŋߎ����邱�Ƃ�����B�ׂ��摥�� ��ɂ��Ă͐�-9.4.3 (3)�� �Q�Ƃ̂��ƁB
�����܂ł̒莮���ŁC�Ⴆ�Ώ�̎�(9.48)�����Ă����炩�Ȃ悤�ɁC
�ǂ̎��ɂ��C�����Y�����͓�x�܂ł������ꂸ�C��x���ꂽ�Y������
���Ă͕K���C2�����Ȃ�1����2�C���邢��3�����Ȃ�1����3�܂�
���a���Ƃ邱�ƂɂȂ��Ă���B
���������āC���̎�(9.48)��![]() �̋L��������
�̋L��������
�Ə�������ŁC�u��x�����Y�����͑��a���Ƃ�v�Ƃ��������Ă�
�S�����͖������낤�B���̋K�������a�K��
�ƌĂсC���̏͂ł́C�ȉ��C���̋K��9.25��p���邱�Ƃɂ���B
�������K�����˂āC���̂悤�Ȍv�Z���������邱�Ƃ��l����
�~�����B![]() ��Kronecker�̃f���^�ł���B
��Kronecker�̃f���^�ł���B
���ɍŌ�̗�̂悤�ɁC��x�����Y�����͂��̃y�A�̂܂܂Ȃ�C ���ł����̕����ɒu�������Ă��S�����͐����Ȃ����Ɠ��ɂ́C ���߂Ɋ���ė~�����B