 |
�ŐV�ł𐳊m�ɓǂޏꍇ�ɂ� pdf �t�@�C�� ���ǂ����B����� web �����̂��߂̊ȈՋ��łł��B
�Ⴆ�܂������̐j������͔C���ɋȂ���ƁC �傫���Ȃ��ό`�����������Ƃɂ͌��̂܂������ȏ�Ԃɂ͖߂�Ȃ��Ȃ�B ����ɐ܂�Ȃ����������͑��̕��������d���Ȃ��Ă��āC���� ���̉ӏ������̂܂������̏�Ԃɂ���͍̂���ł���B �܂��C��x�Ȃ����������t�ɋȂ����肵�āC������J��Ԃ����ό`��^��������ƁC �Ȃ����������̉��x����オ��C�ŏI�I�ɂ͔j�f���邱�Ƃ�����B ���̂悤�Ȕ�t�I��������e�� �ƌĂԂ��C���ɁC�͂����Ƃ��̌`�ƌ��̌`�̍��ł����c���ό`�����ԂƋ��ɂ͕ω����Ȃ��ꍇ�ɂ́C ���̕ό`�ʂ��Y���ό` �ƌĂԁB �c���ό`��������Ƃ������Ƃ́C�Ȃ��邽�߂ɓ��͂����G�l���M�� �ꕔ���C�`�����ɖ߂��ȊO�̃G�l���M�i�M�j�Ƃ��ĎU�킵�Ă��܂������Ƃ� �Ӗ����Ă���C���ꂪ���x�̏オ�闝�R�ł���B ���Ȃ݂ɁC�c���ό`�����ԂƋ��ɕω�����ꍇ�ɂ́C���̓������S�� �ƌĂԁB�}-9.1�Q�ƁB
�Ƃ���ŁC�|�̂悤�Ȍ��������Ȃ猴�q���i�q��ɕ���ł��� ���̌����͂͂��Ȃ�傫���͂��Ȃ̂ŁC �����ɐj���Ƃ����ǂ�����Ȃɗe�Ղɂ͔�t�ό`�������Ȃ��Ǝv����������Ȃ��B �������C���ۂɂ͐}-9.2�̂悤�� �������ׂ������������͖����ɑ��݂���B ���̐}��S��2�ӏ��ł́C���錋���ʁi1�K�j���炻�̏�̌����ʁi2�ʁj�ւ� �点��K�i�̂悤�ɂȂ����Ă���B ����������E�̉ӏ��ł͈قȂ錋���ʂł���㉺�̖ʂ��炻�ꂼ��C �}�̍����̕��ɂ��ǂ��Ă����ƁCS�̉ӏ��œ��������ʂɒB���邱�ƂɂȂ�B ����S�̂悤�Ȍ��ׂ��点��]�� �ƌĂсCE�̂悤�Ȍ��ׂ��n��]�� �ƁiA����E�߂��̂����̊ۂ̒��j�Ă�ł���B ���ۂ̊i�q�_���Ȃ����ʁi1�K�j�ƖԊ|���ۂ� �i�q�_���Ȃ����ʁi2�K�j�Ƃ̌��Ԃ��Ȃ����������]�ʐ� �ƌĂԂ��C���ߓd�q�������ł͂��ꂪ���������Ƃ��Ċώ@�ł���B �����Ėʔ������ƂɁC�͂�������Ƃ��̓]�ʐ����ړ�����̂ł���B �͂��t�����ɂ���Ƌt�����Ɉړ�����B ���������̓]�ʂ��E�ʂ�\�ʂɒB����ƁC�����̐V�����E�ʁE�\�ʂ� �Ȃ��Ă��܂������Ȃ��Ȃ�B �\�ʂ������Ƃ��ɃG�l���M�����o����ĔM���o��B ���ꂪ�c���ό`������������I�Ȏd�g�ł���ƍl��������B
���ď�q�̐j���̎����ł́C�J��Ԃ����x���Ȃ��Ȃ��Ɣj�f�܂ł� ����Ȃ������B����́C������x���ƌĂ������̂��߂ɔS�苭���̂ł��邪�C �j��ɊW���������ޗ��̏d�v�ȓ����ɂ͎��̂悤�Ȃ��̂�����B
���̂悤�ȓ����Ɋ֘A���āC��Ɏ��̂悤�ȎO�̔j��`�Ԃ�����B
�Ɛ��j��Ɣ�J�j��͉����j��Ƃ̓��J�j�Y�����قȂ��Ă��邱�Ƃ�
���炩�ł���C���������邽�߂ɂ͔j��͊w���w�ԕK�v�����邪�C
���҂͋��Ȃ̂ł��̕����ɂ͊܂܂�Ă��Ȃ��B
�Ȃ����͎̏͂�ɁC�A�����J���B��Illinois�BEvanston,
Northwestern��wNemat-Nasser����(1980�N�������j
��`Plasticity'�̍u�`�m�[�g���Q�l�ɂ����B
�܂��C���̏͂̌㔼����́Cp.![]() ��
�K�肷�鑍�a�K���p���Ď���\�����邱�Ƃɒ��ӂ��ė~�����B
��
�K�肷�鑍�a�K���p���Ď���\�����邱�Ƃɒ��ӂ��ė~�����B
���āC�Ԃ̎ԑ̓����v���X���Đ�������Y�����H���V�~�����[�g���邽�߂�C �ޗ������ۂɔj�f���č\���̕���܂ł�\�����Ȃ���Ȃ�Ȃ� �I�Ǐ�Ԃł̐v�ɖ𗧂Ă邽�߂ɂ́C �ޗ��ɂ���Ă͂Ђ��݂����\%���x�ȏ�܂łɎ��邱�Ƃ����邽�߁C ��ό`�i�L���ό`�j��Ԃ܂ł�ΏۂƂ��Ď�舵��Ȃ��Ƃ����Ȃ��ꍇ�������B �������C ���̂悤�Ȉ����ɂ��Ă͏�-12���Q�l�ɂ��ė~�����B ���̏͂ł́C���̑Y���ό`���L�q���郂�f���̍l�������̂��̂� �������ė~�����̂ŁC ����������ό`�̘g�g�ŁC��q�̂悤�ȑY���ό`�� �ޗ������̋L�q�̎d�����������B
���āC�Ⴆ�|���Ƃ���ƁC �ł��P����1�������莎�����Ŋώ@����鎖���ɂ� ���̂悤�Ȃ��̂�����B
���ꂪ���w�I�Y���_���\�z���邽�߂̊�b�ɂȂ�C�|�ȊO�̍ޗ��̃��f���� ��{�ł�����B
���Ȃ݂ɐ}-9.4�ɂ��鉺�̋Ȑ��͓�|�� �T�^�I�ȉ��͂Ђ��݊W�ł���B �ʔ������Ƃɕ���ȕ����C�x���ƌĂ�镔�������邪�C �����ŋN�����Ă��邱�Ƃ��}-9.3�̉��� �}(a)����(b)�ւ̕ω��C�܂�]�ʂ̈ړ��ƏW�ςɑΉ����Ă���B ����C�x��ꂪ�I��������Ƃ̋Ȑ��͐��̌��z�������čd���Ȃ��Ă������C ����́C�}-9.3��(b)�Ɏ������悤�� �W�ς����E�ʓ��̓]�ʂ�������Ȃ邱�Ƃɂ��̌���������B ���̂��Ɖ��͂Ђ��݊W�̓s�[�N���}���C ���̂�����ň����莎���Ђׂ͍��Ȃ��Ă��邪�C ���̂�����Ő}-9.3��(c)�̂悤�� �E�ʔ������������ċ����I�Ȃ��ׂ�ό`������̐����� �����ɂȂ��Ă���ƍl�����Ă���B
�����ł͂܂�1�����̕ό`��Ԃ��ɂ��āC��{�I�ȑY�����f���� ���̋L�q�̎d�����������B �O�߂̎����ώ@���画�f���āC���̂悤�ɍl���Ȃ���Ȃ�Ȃ��B
���̓�ڂ̍��͂킩����������Ȃ��B
�Ⴆ�|�̌�ԍډ����������Đ}-9.5�̂悤��
���͂Ђ��݊W������ꂽ�Ƃ��悤�B
����I�́C�܂���������A![]() B
B![]() C
C![]() D�Ƃ������������ǂ����Ƃ���B
���̎���II�́CA�̂��Ƃɉd�����炷�̂������x�点��E�ւƎ���C
����I�̓_C�Ɠ����Ђ��݃��x��
D�Ƃ������������ǂ����Ƃ���B
���̎���II�́CA�̂��Ƃɉd�����炷�̂������x�点��E�ւƎ���C
����I�̓_C�Ɠ����Ђ��݃��x��![]() �ɒB�����Ƃ����
�d�]����F�Ɏ������Ƃ���B
����Ɏ���III�ł͂܂����k����G
�ɒB�����Ƃ����
�d�]����F�Ɏ������Ƃ���B
����Ɏ���III�ł͂܂����k����G![]() H
H![]() K�Ƃ������������ǂ����Ƃ���B
���̂悤�ɁC
���鉞�͏��
K�Ƃ������������ǂ����Ƃ���B
���̂悤�ɁC
���鉞�͏��![]() �ɂ���ό`��Ԃ́CA, B, E, D, F, H, K��7��ނ����݂��C
�����ˑ��̕ό`�������Ă��邱�Ƃ����炩���B
���R���͂Ђ��݊W�ɂ͈�Έ�W�������B
�܂���q�悤�ɁC�������m�i�������m�j�̊W���\���ł����Ƃ��Ă��C
�����ϕ����邱�Ƃ͂ł��Ȃ�
�ɂ���ό`��Ԃ́CA, B, E, D, F, H, K��7��ނ����݂��C
�����ˑ��̕ό`�������Ă��邱�Ƃ����炩���B
���R���͂Ђ��݊W�ɂ͈�Έ�W�������B
�܂���q�悤�ɁC�������m�i�������m�j�̊W���\���ł����Ƃ��Ă��C
�����ϕ����邱�Ƃ͂ł��Ȃ�
�Ƃ������Ƃ������ł���Ǝv���B
�ȏ�܂������f��������������Ă������C ����f���Y���ɖ��ڂɊW�t�����Ă��� ���Ƃ���l���āC�y�������́u����f���v�̎����̂悤�� �P���Ȃ���f������ΏۂƂ���̂��]�܂����Ǝv����������Ȃ��B �������C1�������� �����莎���ł����Ă��C�����莲����45�x��]���������W�n�Ō���C ����������I�ɂ͂���f���������Ă��邱�Ƃ� �Ȃ��Ă���i�}-9.6�̃C���Z�b�g�Q�Ɓj�̂ŁC �ȉ��ł͍|�̍ޗ������̑�\�ł�������莎���� ����f�����ɓǂݑւ��Đ������悤�B
�I�Ǐ�Ԃ���ɑΏۂƂ���̂ł���C
���ό`�ʂɑ��Ēe���ό`�͔��ɏ������ƍl���Ă�������C
�ŏ��͐}-9.6�̂悤�ɋߎ����āC
�e���ό`�����݂��Ȃ��ޗ����f�����l���Ă݂悤�B
�܂����̍ޗ���
![]() �ȏ�̒�R�͎͂����Ȃ��Ƌߎ�����B
���̂悤�ȕ��̂����E���S�Y����
�ƌĂ�ł���B
����͍\���͊w�ō\���̏I�Ǐ�Ԃ��ȕւɃ��f��������ꍇ��
�悭�p�����郂�f���ł���B
�܂��C�d����苎�낤�Ƃ����Ԃ�����
��ԂƌĂԂ��C�����ώ@�Ɋ�Â��āC
���o�H�͒e���o�H�Ɠ��������������̂Ƃ���B
�ȏ�̒�R�͎͂����Ȃ��Ƌߎ�����B
���̂悤�ȕ��̂����E���S�Y����
�ƌĂ�ł���B
����͍\���͊w�ō\���̏I�Ǐ�Ԃ��ȕւɃ��f��������ꍇ��
�悭�p�����郂�f���ł���B
�܂��C�d����苎�낤�Ƃ����Ԃ�����
��ԂƌĂԂ��C�����ώ@�Ɋ�Â��āC
���o�H�͒e���o�H�Ɠ��������������̂Ƃ���B
�܂�������Ԃ���d���������ꍇ�C�}�̏c���̉��̓��x��![]() ��
�B����܂ł͂Ђ���
��
�B����܂ł͂Ђ���![]() �͐����Ȃ��B
���̉���
�͐����Ȃ��B
���̉���![]() ���~������
�ƌĂԁB�܂�
���~������
�ƌĂԁB�܂�
![]() �ł͒e����ԂȂ̂�
�ł͒e����ԂȂ̂�![]() �ł���B
�ȒP�̂��߂ɁC�~���͈��k�ł�������ł��������̓��x���Ő�������̂Ƃ���B
�d���傫���Ȃ�~�����͂ɒB�������ƁC����Ђ��݂���������Ԃ�
���ׂ�����ƁC�����ł��e���ό`���������Ȃ��̂ŁC���̍��E���S�Y���̂�
�ꍇ�ɂ͂Ђ��݂ɕω��������Ȃ��B
���ׂ�����Ƃ������Ƃ́C
�ł���B
�ȒP�̂��߂ɁC�~���͈��k�ł�������ł��������̓��x���Ő�������̂Ƃ���B
�d���傫���Ȃ�~�����͂ɒB�������ƁC����Ђ��݂���������Ԃ�
���ׂ�����ƁC�����ł��e���ό`���������Ȃ��̂ŁC���̍��E���S�Y���̂�
�ꍇ�ɂ͂Ђ��݂ɕω��������Ȃ��B
���ׂ�����Ƃ������Ƃ́C
![]() �̉��͏�ԂŁC
���̓��x����������ω���^���邱�ƂɂȂ��Ă���̂ŁC
���͂̐��������Ŏg����\���Ƃ��āC
���ׂ�
�̉��͏�ԂŁC
���̓��x����������ω���^���邱�ƂɂȂ��Ă���̂ŁC
���͂̐��������Ŏg����\���Ƃ��āC
���ׂ�
![]() �ƂȂ�u�ԂƂ��ċL�q����̂��֗��ł��낤�B
������
�ƂȂ�u�ԂƂ��ċL�q����̂��֗��ł��낤�B
������![]() �́C�����Ԃ���̕ω��ʁi�����j��\���Ă���B
���̂Ƃ��C��q�̂悤��
�́C�����Ԃ���̕ω��ʁi�����j��\���Ă���B
���̂Ƃ��C��q�̂悤��
![]() �ł��邩��C
������Ԃ���~�����͂ɒB����܂ł̏����~���O�̕ό`������������
�ł��邩��C
������Ԃ���~�����͂ɒB����܂ł̏����~���O�̕ό`������������
�ƋL�q���邱�Ƃ��ł���B
����ɑ��čޗ����~������u�ԁC���邢�͍~��������Ԃ�
�ێ����āC�Y���ό`������������ꍇ�̋L�q���������悤�B
���̂悤�ȕω���Ԃ����ׂɑΉ��������ډ�
��ԂƌĂԁB���ׂƓ��l�̋L�q��p���邱�Ƃɂ���ƁC
�ډׂ�
![]() �Ƃ�������B
�{����
�Ƃ�������B
�{����
![]() �Ƃ������Ƃ��낾���C
���S�Y���ł�
�Ƃ������Ƃ��낾���C
���S�Y���ł�![]() �����Ȃ̂ŁC
�����Ȃ̂ŁC![]() ��
��ȊO�ɂ͂Ȃ�Ȃ�����ł���B���������āC�ډׂ͏��Ȃ��Ƃ�
��
��ȊO�ɂ͂Ȃ�Ȃ�����ł���B���������āC�ډׂ͏��Ȃ��Ƃ�
�ƋL�q�ł���B
�������C![]() �������ɂȂ�̂����߂�K���͂܂������ł��Ă��Ȃ��B
�������ɂȂ�̂����߂�K���͂܂������ł��Ă��Ȃ��B
����ɑ��C�}-9.7�̂悤�ɁC
���E���S�Y���̂ɒe�����l���������̂��e�E���S�Y����
�ƌĂԁB���̏ꍇ��
�ƋL�q�ł��邾�낤�B������![]() �͂���f�e���W��9.5�ł���B
���͂��������ڍׂȋL�q���\�ł��邪�C����͎��߂�
�e�E�Y���d���̂̓��ʂȏꍇ(
�͂���f�e���W��9.5�ł���B
���͂��������ڍׂȋL�q���\�ł��邪�C����͎��߂�
�e�E�Y���d���̂̓��ʂȏꍇ(![]() )�ɂȂ�̂ŁC�����ł͏ȗ�����B
)�ɂȂ�̂ŁC�����ł͏ȗ�����B
�����ƈ�ʓI�ɂ́C�~����̒�R�͈͂��Ƃ͌��炸�C�ό`�����ɔ�����
�傫���Ȃ�̂����ʂł���B
�~����̒�R�͂��ό`�ɔ����đ傫���Ȃ邱�Ƃ��d��
�ƌĂԁB�܂��C�e�E���S�Y���̂����������C�e�����܂ޒe�Y���ޗ��̏ꍇ�ɂ́C
�����Ђ��݂ɒe�������ƑY������������Ƃ݂Ȃ�
�̘a������9.6����B��Y������`e'��`p'�����ꂼ��e��������
�Y��������\���Ă���B�e����Hooke�̖@���ɏ]�����̂Ƃ����
����������B
�ډׂ̏ꍇ�̑Y�������́C���S�Y���̂Ɠ��l
![]() �Ƃ�������̂�
�Ƃ�������̂�
�ƒu�����Ƃɂ���B���̊W�����ꑥ
�ƌĂ�ł���B����![]() �͍ޗ��p�����[�^9.7�ł͂Ȃ��C
���͑���
�͍ޗ��p�����[�^9.7�ł͂Ȃ��C
���͑���![]() �ɂ��W�����ʁC
�Ⴆ��
�ɂ��W�����ʁC
�Ⴆ��
![]() �ł���C
�e���E���ׁE�ډׂɑ���
�ł���C
�e���E���ׁE�ډׂɑ���
��������̂ł���B�������C�~����̈��ł͂Ȃ���R�͂�
���f�������邽�߂ɁC�~������![]() �͈��ł͂Ȃ��C
�����Ɉˑ��������ɂȂ�Ƃ�������̂ŁC
�Ⴆ�����ł�
�͈��ł͂Ȃ��C
�����Ɉˑ��������ɂȂ�Ƃ�������̂ŁC
�Ⴆ�����ł�
![]() ��
�L�q�����B
��
�L�q�����B
![]() ��
��
![]() ��
�������̐ϕ��ʂł���B
��ʂɎ�(9.6)��
��
�������̐ϕ��ʂł���B
��ʂɎ�(9.6)��
![]() �Ə������Ƃ��ł��C
�����ϕ��i�ł���j����
�Ə������Ƃ��ł��C
�����ϕ��i�ł���j����
�̂悤�ȍ����̔���`�W�ɂȂ�̂���ʓI�ł͂��邪�C
���̐߂ł͊ȒP�̂��߂ɐ}-9.8�̂悤��
���`�W��������̂Ƃ���B
�܂��C�~������![]() �����ł͂Ȃ����Ƃ���C
�ډׂ̏�����
�����ł͂Ȃ����Ƃ���C
�ډׂ̏�����
![]() ����
����
![]() ��
�g��������B
��
�g��������B
��ʂɂ͎�(9.4)�ɂ���悤�ɁC�����Ђ��݂̒e��������
�Y�������̘a���������Ђ��ݗʂɂȂ邪�C
�����ł͂������������I�ȗ�����[�߂邽�߂ɁC�������S�Ђ��ݗ��_
�ʼn��肳���悤�ɁC���Ђ��ݗʓ��m�ɂ����l�̉��Z������������ꍇ��
�l���Ă݂悤�B
����͔����ό`�͈̔͂ŁC���ׂ������Ȃ�
���`�d����1�����̒P���ډ�ԂɌ��肷��C���܂���͖������낤�B
�܂�
������������̂Ƃ��C�e������
������������̂Ƃ���B�}-9.8����C
�~����Ԃɏ�ɂ��鐳�̉��͂́C�Ђ��݂�
�̊W�ɂ���C����Ɏ�(9.8) (9.9)���������
�ƂȂ邩��C���������
�Ƃ����W�ɂȂ�B����![]() �͍~����Ԃ���ɖ������Ă��邱�Ƃ���C
�E�ӂ�
�͍~����Ԃ���ɖ������Ă��邱�Ƃ���C
�E�ӂ�
![]() ��
����C
��
����C
![]() ���ϕ��ł���Ƃ����̂ŁC
����ɂ����
���ϕ��ł���Ƃ����̂ŁC
����ɂ����
![]() ��
���邱�Ƃ��킩��B�܂�C
���`�d�����~�����͂́C�P���ɂ�
��
���邱�Ƃ��킩��B�܂�C
���`�d�����~�����͂́C�P���ɂ�
(9.11)
�Ń��f�����ł���B![]() �͂��̍d���̕ω�����^����̂ŁC�d���W��
�ƌĂ��ޗ��p�����[�^�ł���B�}-9.9��
���̗l�q��`�����B���̂��Ƃ���C
�~����Ԃ��K�肷���~������
��
�͂��̍d���̕ω�����^����̂ŁC�d���W��
�ƌĂ��ޗ��p�����[�^�ł���B�}-9.9��
���̗l�q��`�����B���̂��Ƃ���C
�~����Ԃ��K�肷���~������
��
�Ɨ^����������Ƃ��킩��B![]() ���~����
�ƌĂԁB
����ɑ�
���~����
�ƌĂԁB
����ɑ�![]() �́C���͂Ђ��݊W��̒e�����܂��������
�d���W���ł���C�����ő���ł���̂�
�́C���͂Ђ��݊W��̒e�����܂��������
�d���W���ł���C�����ő���ł���̂�![]() �̕��ł���B
�̕��ł���B
���̂悤�ȉ��肪��������ꍇ��![]() �̋�̓I�ȕ\�������߂Ă������B
�ȒP�̂��߂�
�̋�̓I�ȕ\�������߂Ă������B
�ȒP�̂��߂�![]() �ōl����B�~�����ď�ɍډ�Ԃɂ���C
��ɑY���Ђ��ݑ��������Ő���������B���̂Ƃ��C��(9.12)��
�~�������͏�ɖ������ꑱ���Ȃ���Ȃ�Ȃ��B����������
���̕ω��͗�ł��葱����B��(9.12)�̑������Ƃ�ƁC�����
�ōl����B�~�����ď�ɍډ�Ԃɂ���C
��ɑY���Ђ��ݑ��������Ő���������B���̂Ƃ��C��(9.12)��
�~�������͏�ɖ������ꑱ���Ȃ���Ȃ�Ȃ��B����������
���̕ω��͗�ł��葱����B��(9.12)�̑������Ƃ�ƁC�����
��������������B�������������
�ƌĂԁB���̍Ō�̍��Ɏ�(9.6)�������邱�Ƃɂ����
�Ƌ��߂���B�ډ�Ԃł�
![]() �ł��邵�C
�ł��邵�C![]() �͈�ʂ�
�e������
�͈�ʂ�
�e������![]() ���͏��������Ƃ���
���͏��������Ƃ���![]() �ƂȂ�̂ŁC
�ƂȂ�̂ŁC![]() ����������B
��(9.13)�̖��̉E�̍ŏ��̕\���ɂ́C���q�E�����
����������B
��(9.13)�̖��̉E�̍ŏ��̕\���ɂ́C���q�E�����![]() ��
�����ď璷�ȕ\���ɂȂ��Ă��邪�C
��q��3�����ł̕\���Ƃ̔�r��e�Ղɂ��邽�߂Ɋ����ėp�����\���ł���B
�Ō�̕\���ł́C�����
��
�����ď璷�ȕ\���ɂȂ��Ă��邪�C
��q��3�����ł̕\���Ƃ̔�r��e�Ղɂ��邽�߂Ɋ����ėp�����\���ł���B
�Ō�̕\���ł́C�����![]() ���~��������(9.12)��
�������Ă���̂ŁC
���~��������(9.12)��
�������Ă���̂ŁC
![]() �Œu�������Ă���B
�Ȃ������ł́C1�������f���ł����ɑS�Ђ��ݗ��_��p�������߁C
��(9.6)�̊�{�I�ȉ���
�w�Y���Ђ��ݑ����͉��͂Ɠ��������ɂ���x�Ƃ������{�����Ƃ͈قȂ�C
�Y���Ђ��ݑ��������͑����ɂ��̂܂ܔ�Ⴕ���\����(9.13)��
�Ȃ��Ă��܂��Ă���i�����I�ɂ͈قȂ�\���Ɍ�����j���Ƃɂ�
�\���ɒ��ӂ��ė~�����B
�Œu�������Ă���B
�Ȃ������ł́C1�������f���ł����ɑS�Ђ��ݗ��_��p�������߁C
��(9.6)�̊�{�I�ȉ���
�w�Y���Ђ��ݑ����͉��͂Ɠ��������ɂ���x�Ƃ������{�����Ƃ͈قȂ�C
�Y���Ђ��ݑ��������͑����ɂ��̂܂ܔ�Ⴕ���\����(9.13)��
�Ȃ��Ă��܂��Ă���i�����I�ɂ͈قȂ�\���Ɍ�����j���Ƃɂ�
�\���ɒ��ӂ��ė~�����B
���̂悤�ɁC
�Y���͒e���Ƃ͑傫���قȂ�C1)��Ԃ��`����W���i
![]() �̂ǂ̏�Ԃ��j�ƁC2)�ό`�̕ω������`����
�W���i
�̂ǂ̏�Ԃ��j�ƁC2)�ό`�̕ω������`����
�W���i![]() �͂ǂ̂悤�ȋK�������邩�j�́C
��̏������K�肷��K�v������B
�܂��C��Ԃ��ډׂȂ̂����ׂȂ̂��ɂ��Ă��C
���̓�̏����ƓK������悤�ɒ�`����K�v������B
�ȉ��C
�܂�2��ނ̋K�����K�v�Ȃ��Ƃɂ��āC���C�Ƃ��ׂ���ɂ���
�������悤�B�}-9.10�Ɏ������̂́C
����߂̗�
�͂ǂ̂悤�ȋK�������邩�j�́C
��̏������K�肷��K�v������B
�܂��C��Ԃ��ډׂȂ̂����ׂȂ̂��ɂ��Ă��C
���̓�̏����ƓK������悤�ɒ�`����K�v������B
�ȉ��C
�܂�2��ނ̋K�����K�v�Ȃ��Ƃɂ��āC���C�Ƃ��ׂ���ɂ���
�������悤�B�}-9.10�Ɏ������̂́C
����߂̗�![]() �ŏ����S���������Ă���ł���B
�S���̒e���̂��߁C�����S���͎�c��ł���B
�����āC���̏��Ə����S���̊Ԃ̐Î~���C�W��
��
�ŏ����S���������Ă���ł���B
�S���̒e���̂��߁C�����S���͎�c��ł���B
�����āC���̏��Ə����S���̊Ԃ̐Î~���C�W��
��![]() �Ƃ���ƁC�����S�������ׂ�n�߂�\���́C������
�Ƃ���ƁC�����S�������ׂ�n�߂�\���́C������
�ŗ^�����邪�C�����ł͎��ۂɂ͂��ׂ�Ȃ����̂ƍl���ė~�����B
���̏�ԂŁC�Ⴆ��
![]() ,
, ![]() �Ƃ����ꍇ�ɂ́C�ő喀�C��
�����邹��f�O�͂���p�������ƂɂȂ�C�㎮��
�Ƃ����ꍇ�ɂ́C�ő喀�C��
�����邹��f�O�͂���p�������ƂɂȂ�C�㎮��
�̂悤�ȕω��������C![]() �̕����ł��鏰�����C
�܂�
�̕����ł��鏰�����C
�܂�![]() �̕����ɂ��ׂ�n�߂�B
�ł͎���
�̕����ɂ��ׂ�n�߂�B
�ł͎���
![]() ,
, ![]() �Ƃ��Ă݂悤�B
�܂�͂��̂ł��邪�C���̏ꍇ�ɂ͒e���Ƃ̍��������Ɩ��m��
�Ƃ��Ă݂悤�B
�܂�͂��̂ł��邪�C���̏ꍇ�ɂ͒e���Ƃ̍��������Ɩ��m��
�ƂȂ�̂ŁC���̂Ƃ������ׂ�n�߂邪�C���ׂ�����͉������ϓ�![]() �Ƃ�
�W���Ȃ��C����ƒ�������������
�܂�
�Ƃ�
�W���Ȃ��C����ƒ�������������
�܂�![]() �̕����ł��邱�Ƃ�
���ӂ��ė~�����B
�ł�
�̕����ł��邱�Ƃ�
���ӂ��ė~�����B
�ł�
![]() ,
, ![]() �̏ꍇ�͂ǂ����낤�B
���̂Ƃ���
�̏ꍇ�͂ǂ����낤�B
���̂Ƃ���
�̂悤�ɁC���ׂ�n�߂�\���̏����������܂܂Ȃ̂ŁC
�����ł͂��ׂ�Ȃ����ƂɂȂ�B
�Ō�ɗ͂̌�����ς���
![]() ��
�����ꍇ�ɂ́C
��
�����ꍇ�ɂ́C
![]() ,
,
![]() �Ȃ��
�Ȃ��
�ƂȂ�C���̂Ƃ���![]() �̕����ɂ��ׂ�n�߂邱�ƂɂȂ�B
�̕����ɂ��ׂ�n�߂邱�ƂɂȂ�B
���̂悤�ɁC��Ԃ��K�肷���![]() �����ł���Ώ����S����
�e���ό`���邾���ł���C��
�����ł���Ώ����S����
�e���ό`���邾���ł���C��![]() ����ɂȂ����Ƃ��ɁC��t�I�ȉ^����
������u�\���v����������B�����āC���̊��������悤�Ƃ����Ƃ��ɁC
���ۂɂ��ׂ�^����������̂ł���B
���̂悤�Ȃ��ׂ�n�߂�������d�v�����C���ꂪ��q��1)�̊W���ł���B
����C���̉^���̌����́C
�O�͕ϓ����p�̌����̕ϓ��Ƃ͖��W�ɁC��ɏ��ɉ����������C
���������������f��
����ɂȂ����Ƃ��ɁC��t�I�ȉ^����
������u�\���v����������B�����āC���̊��������悤�Ƃ����Ƃ��ɁC
���ۂɂ��ׂ�^����������̂ł���B
���̂悤�Ȃ��ׂ�n�߂�������d�v�����C���ꂪ��q��1)�̊W���ł���B
����C���̉^���̌����́C
�O�͕ϓ����p�̌����̕ϓ��Ƃ͖��W�ɁC��ɏ��ɉ����������C
���������������f��![]() �̕�����
�̕�����
�̂悤�ɐ����邱�ƂɂȂ�B
�㎮��
![]() ��
�ݐς��}-9.10��
��
�ݐς��}-9.10��
![]() �ł���B
�����āC���̂��ׂ�^���͗͂������Ă����ɂ͖߂�Ȃ�����C
��t�I�ȉ^���ł���B
�������t�����ɗ͂�������Ό��̕����ɖ߂邪�C
���Ƃ̖��C�ŔM�ƂȂ��ē������G�l���M�͌��̍ޗ��ɖ߂邱�Ƃ͂Ȃ��B
����
�ł���B
�����āC���̂��ׂ�^���͗͂������Ă����ɂ͖߂�Ȃ�����C
��t�I�ȉ^���ł���B
�������t�����ɗ͂�������Ό��̕����ɖ߂邪�C
���Ƃ̖��C�ŔM�ƂȂ��ē������G�l���M�͌��̍ޗ��ɖ߂邱�Ƃ͂Ȃ��B
����
![]() �̏�������q��2)�̊W���ł���B
�Y���ό`�́C���̖��C��R�Ƃ��ׂ�̊W�ɂ悭�������ۂł���B
������
�̏�������q��2)�̊W���ł���B
�Y���ό`�́C���̖��C��R�Ƃ��ׂ�̊W�ɂ悭�������ۂł���B
������![]() ����Ԃ��`������ł���C
����Ԃ��`������ł���C![]() ��
�Y����ԁi��q�̍~�������j��\���W���ł���C
���̕ω�
��
�Y����ԁi��q�̍~�������j��\���W���ł���C
���̕ω�![]() �Ɋւ���@����
�Y���ό`�̕ω����i��q�̔��W���j���`����W���ɂȂ�B
�Ɋւ���@����
�Y���ό`�̕ω����i��q�̔��W���j���`����W���ɂȂ�B
���āC���̑������K�肷������ɂ��āC
�e���̏ꍇ
![]() �Ɣ�ׂĂ݂悤�B
�e���̏ꍇ�́C�Ⴆ��
�Ɣ�ׂĂ݂悤�B
�e���̏ꍇ�́C�Ⴆ��![]() �𑝂₷
�𑝂₷
![]() �ƁC
�����S���͉��������ɂ���ɏk�����Ƃ��邾�낤�B
�܂����C��R�������Ă�����
�ƁC
�����S���͉��������ɂ���ɏk�����Ƃ��邾�낤�B
�܂����C��R�������Ă�����
![]() ��
��![]() �𑝂₷�ƁC
�����S���͘c�����Ƃ��邾�낤�B�܂�C
�e�����
�𑝂₷�ƁC
�����S���͘c�����Ƃ��邾�낤�B�܂�C
�e�����
![]() ���邢��
��t�^���������Ȃ��ꍇ
���邢��
��t�^���������Ȃ��ꍇ
![]() �ɂ͒e���ω������������C
���������̕ό`�́C�O�͕ϓ����p�̌����̕ϓ��ɒ���
�ɂ͒e���ω������������C
���������̕ό`�́C�O�͕ϓ����p�̌����̕ϓ��ɒ���
�̂悤�ɊW����̂ł���B������![]() �͈���Young���ł���B
�������C�e���̏ꍇ�ɂ͗͂������Ό��ɖ߂�B
���̒e���̊W�������ӁE�E�ӂ�
�͈���Young���ł���B
�������C�e���̏ꍇ�ɂ͗͂������Ό��ɖ߂�B
���̒e���̊W�������ӁE�E�ӂ�![]() �̕t������
��̂��ׂ�ό`�̏ꍇ�ƈقȂ����ƂɋC�t���ė~�����B
�̕t������
��̂��ׂ�ό`�̏ꍇ�ƈقȂ����ƂɋC�t���ė~�����B
�Ƃ���ŁC�}-9.10�̂悤��
![]() ��
���������Ɨ͂������ƁC���̂܂܂̏�ԂŎ~�܂�B
�����ł���ɗ͂l�ɉ����Ă����ƁC��͂�
��(9.14)�����ɐ����������ƂɁC
�܂����ׂ�n�߂邾�낤�B
�܂�C��t�^���̊J�n�́u�́v�ŗ^����������
���߂��Ă��邱�Ƃɂ͒��ӂ��悤�B
�������C
�`���I�Ɏ�(9.14)�����炩�̒e���W��
��
���������Ɨ͂������ƁC���̂܂܂̏�ԂŎ~�܂�B
�����ł���ɗ͂l�ɉ����Ă����ƁC��͂�
��(9.14)�����ɐ����������ƂɁC
�܂����ׂ�n�߂邾�낤�B
�܂�C��t�^���̊J�n�́u�́v�ŗ^����������
���߂��Ă��邱�Ƃɂ͒��ӂ��悤�B
�������C
�`���I�Ɏ�(9.14)�����炩�̒e���W��![]() �Ŋ����
�Ŋ����
�̂悤�Ɂu�Ђ��݁v�ŕ\�����Ƃ��\�ł���B�������C
��q�̂悤�ȗ͂������ččډׂ����O���ɒu���C
�w����![]() �ɑY���I�ȂЂ��݂̗ݐϐ���
�ɑY���I�ȂЂ��݂̗ݐϐ���
![]() ��
�܂߂��ꍇ�ɁC
��t�^���̊J�n�������u�Ђ��݁v�ŕ\�����Ƃ͂ł��Ȃ��x�Ƃ������Ƃ�
�����ł���Ǝv���B
��
�܂߂��ꍇ�ɁC
��t�^���̊J�n�������u�Ђ��݁v�ŕ\�����Ƃ͂ł��Ȃ��x�Ƃ������Ƃ�
�����ł���Ǝv���B
1�������͏�Ԃ̊ȒP�ȉ��p��͍\���v�f�ł���B
���ɒe�E���S�Y���̂̏ꍇ�ɂ��Ă�
����[79]�ɑ�\�I�ȗႪ����̂ŁC
��������܂������邢�̓g���X���ނ�ΏۂƂ���
���ʂ݂̂������Ă������B
�������C�g���X����̏ꍇ�ɂ͂���f���͂ł͂Ȃ������͂�1�������͏�Ԃ�
���邽�߁C�O�߂܂ł̋c�_�����ׂĒ����͂Œu����������ŁC
�S�Ђ��ݗ��_�܂葝���͗p���Ȃ��\���ŕ\���Ă������B
�܂�C�e����Young����ʂ���1�����̉���![]() �ƂЂ���
�ƂЂ���![]() ��
���`��
��
���`��
![]() �ŕ\������Ă�����̂Ƃ��C
�ŕ\������Ă�����̂Ƃ��C![]() ��
�������鏉���~�����͂�
��
�������鏉���~�����͂�
![]() �Ƃ��C���̂Ƃ���
�~���Ђ��݂�
�Ƃ��C���̂Ƃ���
�~���Ђ��݂�
![]() �Ƃ���B
�Ƃ���B
�}-9.11�Ɏ������s�Ò�g���X�̏ꍇ
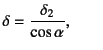 �������C
�������C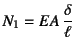 ,
,
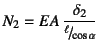 �C
�~����́C
�C
�~����́C
�ł���B������![]() �͒f�ʐς�3�{�Ƃ������Ƃ����B2�{�Ƃ�
�e����Ԃł����
�͒f�ʐς�3�{�Ƃ������Ƃ����B2�{�Ƃ�
�e����Ԃł����
�ł��邩��
�ƂȂ邽�߁C�����ނ���ɍ~�����邱�Ƃ��킩��B
�����ނ��~������̂�
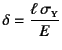 �̂Ƃ��ŁC
���̌��
�̂Ƃ��ŁC
���̌��
�Ƃ����W�����藧�B
���̌�
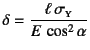 �Ŏނ�
�~�����C���̂���
�Ŏނ�
�~�����C���̂���![]() �͕s��ƂȂ�B
���̗������������̂��}-9.11�ł���B
������
�͕s��ƂȂ�B
���̗������������̂��}-9.11�ł���B
������
�ƒ�`�����B
![]() �͏����~�����͂ł���B
���̌��_�ŏd�v�Ȃ��Ƃ́C�ŏI�I�ȉd�ł���I�ljd
�͏����~�����͂ł���B
���̌��_�ŏd�v�Ȃ��Ƃ́C�ŏI�I�ȉd�ł���I�ljd![]() ��
��
![]() �ƂȂ�C
�s�Ò�\���ł����Ă��e���W���Ɉˑ����Ȃ��Ƃ������Ƃł���B
�܂�C���Y���̂Ƃ��Ă��̏I�ljd�����߂邱�Ƃ��ł���\�����C
���̊ȒP�ȉ�͗�͎����Ă���B
���ꂪ�C��-9.5�Ŏ���
�Y����͂�Ɍ���͂ɒʂ��Ă���ƍl���ė~�����B
�v�ɂ����Ă͕֗��ŗL�p�ȏ��ł���B
�ƂȂ�C
�s�Ò�\���ł����Ă��e���W���Ɉˑ����Ȃ��Ƃ������Ƃł���B
�܂�C���Y���̂Ƃ��Ă��̏I�ljd�����߂邱�Ƃ��ł���\�����C
���̊ȒP�ȉ�͗�͎����Ă���B
���ꂪ�C��-9.5�Ŏ���
�Y����͂�Ɍ���͂ɒʂ��Ă���ƍl���ė~�����B
�v�ɂ����Ă͕֗��ŗL�p�ȏ��ł���B
���ɏ��Ȃ����Ă�������ނ�ΏۂƂ���B
���̏ꍇ�͒f�ʓ��Œ����͎͂O�p�`���z�����Ă��邽�߁C
��`�f�ʂ��Ƃ����ꍇ�̉E�}-9.12�̂悤��
�O�̏�Ԃ��l������B
���[��(a)�Ɏ���܂ł��e����Ԃł���C(b)�̏�Ԃł�
����������![]() ���ꂽ�_�܂ł��e���ł��̊O�����~�����Ă���B
���ꂪ�ŏI�I�ɂ�(c)�̋Ɍ���ԂɎ���C����ȏ�̊O�͂�
��R�ł��Ȃ����Ƃ���C����͏I�Ǐ�Ԃł���B
���̂Ƃ��Ȃ����[�����g
���ꂽ�_�܂ł��e���ł��̊O�����~�����Ă���B
���ꂪ�ŏI�I�ɂ�(c)�̋Ɍ���ԂɎ���C����ȏ�̊O�͂�
��R�ł��Ȃ����Ƃ���C����͏I�Ǐ�Ԃł���B
���̂Ƃ��Ȃ����[�����g![]() �Ƌȗ�
�Ƌȗ�![]() �̊W�ׂĂ݂悤�B
�e����Ԃł�
�̊W�ׂĂ݂悤�B
�e����Ԃł�
�Ƃ����W�ɂȂ�B������![]() �͍ŊO�����͂̑傫���ł���C
�͍ŊO�����͂̑傫���ł���C![]() ��
�f�ʌW���ł���B��}��(a)�̏�Ԃ́C
��
�f�ʌW���ł���B��}��(a)�̏�Ԃ́C![]() ���~�����͂�
�B�����Ƃ��ɑ������邽�߁C
���̂Ƃ��̋Ȃ����[�����g��
���~�����͂�
�B�����Ƃ��ɑ������邽�߁C
���̂Ƃ��̋Ȃ����[�����g��![]() �i�~�����[�����g
�ƌĂ��j�Ƃ����
�i�~�����[�����g
�ƌĂ��j�Ƃ����
�ɂȂ�B������![]() �͏����~�����̋ȗ��ł���B
����ɉd�������Ēe�Y����ԁi�}��(b)�j�ɂȂ��
�͏����~�����̋ȗ��ł���B
����ɉd�������Ēe�Y����ԁi�}��(b)�j�ɂȂ��
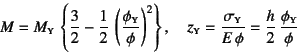
����������B����ɋȗ���������ɂȂ�![]() �ŏ�}��(c)�̋Ɍ����
�ŏ�}��(c)�̋Ɍ����
�Ɏ���B
����![]() ���S�Y�����[�����g
�ƌĂ�邪�C������e���Ƃ͖��W�ł���B
���S�Y�����[�����g
�ƌĂ�邪�C������e���Ƃ͖��W�ł���B
�O�߂̌��ʂ𗘗p���Đ}-9.13�̂悤��
���[�P���x������3�_�Ȃ�����͂��Ă������B
�����f�ʂ��ŏ��ɍ~�����邱�Ƃ͖��炩�ł���C
���̌�C���̐}�̂悤�ɒ����t�߂�![]() �̗̈�Œf�ʂ̈ꕔ���~������B
���[����
�̗̈�Œf�ʂ̈ꕔ���~������B
���[����![]() �����Ƃ�ƁC
�����Ƃ�ƁC![]() ��
�Ƃ�
��
�Ƃ�
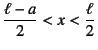 �͈̔͂Œe�������̑傫����
�͈̔͂Œe�������̑傫����
�ł���C�����̂����
![]() ��
��
�Ƌ��߂���B������![]() �͒����������~������Ƃ��̊O�͂ł���
�͒����������~������Ƃ��̊O�͂ł���
�ƒ�`�����B
![]() �͒����f�ʂ������~������Ƃ���
�����̂���݂ł���B�㎮�̕������̒����疾�炩�Ȃ悤��
�͒����f�ʂ������~������Ƃ���
�����̂���݂ł���B�㎮�̕������̒����疾�炩�Ȃ悤��
�܂ł������͑��݂����C![]() ��
�������Ƃ���
��
�������Ƃ���
![]() �C
�܂�X�p�������őS�f�ʍ~���������Ă��܂��C�����ŗ���
�܂�Ȃ���C�܂�ȗ���������ɂȂ�C����ȏ�̉d�ɂ�
��R�ł��Ȃ��Ȃ�B�}-9.14�ɂ��̒e�Y���������܂Ƃ߂��B
�C
�܂�X�p�������őS�f�ʍ~���������Ă��܂��C�����ŗ���
�܂�Ȃ���C�܂�ȗ���������ɂȂ�C����ȏ�̉d�ɂ�
��R�ł��Ȃ��Ȃ�B�}-9.14�ɂ��̒e�Y���������܂Ƃ߂��B