- ...
単結晶粒中に9.1
- 単結晶毎に結晶面の向きが異なるから界面には最初から転位が存在しているが,
図には省略した。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 塑性変形を生じさせ続けると,弾性変形9.2
- ゴムのように,弾性挙動も非線形性を示す材料は多数存在する。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
塑性変形はほとんど9.3
- 砂・岩・複合材料のような内部に微視構造を持つ材料では
その限りではない。鋼も多結晶材料であり,内部に微視構造を
持つが,等方応力状態での塑性変形は非常に小さいと考えている。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
応力レベルよりも低い応力レベルで,塑性変形が生じる9.4
- 非均質性が助長するため,特に内部に微視構造を持つ場合(例えば文献[43]
[50])に生じ易い。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...はせん断弾性係数9.5
- この章では,
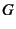 ではなく
ではなく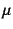 でせん断弾性係数を表す。
でせん断弾性係数を表す。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...の和が成立9.6
- ただし
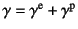 は成立しないことは
除荷を考えれば当然である。
は成立しないことは
除荷を考えれば当然である。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...は材料パラメータ9.7
- もし
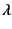 が材料パラメータである場合には,
式(9.6)は粘性抵抗を表す。
が材料パラメータである場合には,
式(9.6)は粘性抵抗を表す。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
時間の単位を有しない無次元量9.8
- 文献によっては誤解を避けるために,例えば
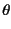 を
履歴を表す単調増加無次元パラメータとして
を
履歴を表す単調増加無次元パラメータとして
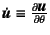 と定義しているが,
この文書では面倒なので記号
と定義しているが,
この文書では面倒なので記号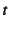 を用いている。
を用いている。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
であること9.9
- 塑性ひずみ増分の代表的な原因である
転位は欠陥であり,適合場ではないことは明らかだ。それを調整して
連続体としての適合場にするための弾性ひずみ増分も,したがって適合場では
なくなる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...kitagawa2]成立9.10
- 著者は前者を支持している。式(12.72)の説明部分を
参照のこと。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
はず9.11
- 客観性の一つ。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
(つまり塑性ひずみ増分の第2不変量9.12
- ここでは塑性的体積変形は無いと仮定しているので,
塑性ひずみ増分の第1不変量は零である。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...相当量の累積9.13
- 累積塑性ひずみは第1著者の造語である。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...という関係にある9.14
- 道路橋示方書[128]のせん断強度
はこれを根拠にしている。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
と呼ばれ9.15
- これをMises応力と呼ぶのはやめませんかねぇ。汎用プログラムのマニュアルや
出力にでも書いてあるのだろうかしらん。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...向きを持った面上9.16
- 単結晶体の場合には結晶格子の稠密面に相当する。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
摩擦抵抗を無力にし,すべりの発生9.17
- その面上を,転位
と呼ばれる格子欠陥が移動し始めることに相当する。
なお,一旦動いた転位は,界面や表面に達しないうちは,
外力の向きを変えたときに反対に動くことも
よく知られている。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
すべる(転位が動く)可能性9.18
- 実際の単結晶の破断面がこのような稠密面とは必ずしも同じではないのは
興味深い。ミクロとマクロの間には亜空間
でもあって,そこには魔物が棲んでいるのだろう。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
このすべり面上でのすべり変形しか9.19
- 結晶系金属の場合には,結晶格子の稠密面上の転位の移動によるせん断変形が
主な塑性変形であるため,塑性的な体積変形は発生しない。
これに対し,砂地盤等を連続体として取り扱う場合には,せん断に対して,
砂粒が隣の砂粒に乗り上げるような変形も伴いながらすべるため,
塑性的な体積変形(ダイレタンシー
)が生じることがある。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
を有している9.20
- 弾性を無視しない限り決して非圧縮的な変形にはならないが,
弾性ひずみが塑性ひずみよりもかなり小さい場合が普通であることから,
数値解析等で,総適合ひずみがほぼ非圧縮性を有している場合が
あり得る。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...ことになり,そういう意味では「水9.21
- 式(3.101)の連続の式と体積変形零の式は同じ条件である。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
この偏差応力テンソルと応力増分テンソル9.22
- ここで言う応力増分というのはもちろん,材料中に生じる抵抗力の変化を
表現できなければならないのは当然である。
しかし,ここで示しているように応力速度で単純にその
応力増分を表現した場合,材料が剛体的に回転するだけでも
その応力速度テンソルの各成分は零にはならないから,
単純な応力速度を構成方程式に用いることができないのは明らかである。
ただし,微小変形理論の枠内ではこれが問題になることはないので,
この章では特に応力速度の定義については議論しない。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...ということ9.23
- 文献[25]では積分記号が用いられているが,本文中の説明では
「台数和(algebraic sum)」と明記して区別してある。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...を一致させて1から3まで和をとる9.24
- 縮約
と呼ばれる演算であり,物理的には体積変形増分を求めている。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
と呼び,この章では,以下,この規約9.25
- ただし,これは直角座標でしか用いることができない
不正確な定義である。正確な定義は付録-Jに
示す。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
それは,等方応力では降伏しない9.26
- 複合材料のように内部に微視構造を持つ材料の場合は,
例えば各相がMisesの降伏条件に従う材料であっても,巨視的には
等方応力で降伏[142]する。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...で与えられる9.27
- ただし,Trescaの降伏関数の場合には,図-9.19からも
明らかなように降伏曲面に角点
が存在することから,式(9.61)の微係数が唯一には
定義できない問題点がある。角点の発生は,多結晶体のように
複数の降伏メカニズムが存在する場合に,その複数の降伏曲面の
一番内側の包絡面で降伏曲面を定義する[43]ことからも生じる。
これについては文献[92]あるいは節-9.4.3で
紹介するモデル[65]等を参照のこと。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...の外向き法線「ベクトル」9.28
- 円の方程式
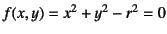 を
を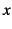 と
と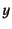 で微分して求められる
ベクトル
で微分して求められる
ベクトル
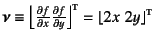 が円の外向き法線
ベクトルを表していることからもわかるだろう。
が円の外向き法線
ベクトルを表していることからもわかるだろう。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
弾性や流れ則等の構成則は増分についての線形関係のみでモデル化9.29
- 岸野先生がこの件についてコメントしてくださったのだが,
一つのわかり易い例として中立載荷条件を挙げてくださった。
増分が小さくないのであれば中立載荷条件は載荷条件になってしまうからである。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...と9.30
-
ここはわからない。なぜかについては文献を勉強して欲しい。
原点に転位があって
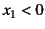 が
が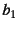 だけずれた転位による
変形勾配が
だけずれた転位による
変形勾配が
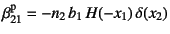 というのは,
どうやら認識はできてはいるが。
というのは,
どうやら認識はできてはいるが。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...現象論的9.31
- 英語の`phenomenological'の直訳で,観察をそのままモデルにしたという
意味で使っている。これは相応しくないという査読意見を
いただいたこともあるが,理由が理解できなかった。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (特性長さ)\fakejchar9.32
- 例えば,多結晶体中の単結晶の粒径や,転位に関係した長さや密度等。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...体積変形の塑性成分9.33
-
地盤工学でダイレタンシー
と呼ばれるものに対応している。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
大きな変形になるにつれて降伏条件を満足しなくなる9.34
- 文献[65]は,ある変形状態の接線的な力学現象を
扱っているので,この近似による不具合は生じない。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
なおこの節は,Northwestern大学の村教授9.35
- 第1著者は個人的にもたいへんお世話になり,2008年秋には
まだまだお元気だったのですが,2009年8月9日お亡くなりになりました。
たいへん残念です。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...の方向9.36
- 平面問題は3次元問題であり,その平面外方向の主応力は式(9.163)から
わかるように,中間主応力
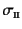 になる。
になる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...mm1,mm2,mm3,spencerを参照9.37
- 要約は文献[61]に示した。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
求めたい崩壊モードということになる。それが図の右端のモード9.38
- 土木構造物としては相応しくない設計であるが。呵呵。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...のレベル9.39
- もちろん,この中央断面でも損傷が進んで
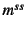 の状態が
保持できるとは限らない。図-9.62の
「崩壊」への履歴。
の状態が
保持できるとは限らない。図-9.62の
「崩壊」への履歴。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...とすればいい9.40
- Voigtではなくちょっと工夫した平均化を用い[50]ても,
降伏条件は同様になる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
寸法のような長さの平方根9.41
- 力学理論中に長さの平方根が存在すると,理論を
無次元表示することが一般にはできなくなる。
コンクリート構造や地盤や岩盤等は,
寸法比率が同じであっても,10cm程度の対象と1m程度の
対象とはお互いに異なる挙動を示すことがある。
これを寸法効果
と呼ぶが,そういった効果を表現するためには特性長さが
必要である。特性長さを含む理論も一般には無次元化できない。
悩ましいのは,導入した特性長さに敏感な結果を生じるモデルは
適切ではないとされていることだ。微妙なサジ加減のパラメータを
物理的考察で探すことが必須である。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.