 |
最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
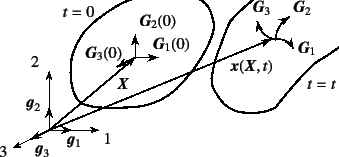
時刻のような単調増加する履歴パラメータ![]() の
の![]() を
初期状態,その状態における物体の状況を初期配置
と呼ぶ12.2ことにし,
その物体が移動し変形して
を
初期状態,その状態における物体の状況を初期配置
と呼ぶ12.2ことにし,
その物体が移動し変形して![]() に至った状況を現配置
と呼ぶ。
物体の状況とは関係無く,空間に固定した直角座標を定義し,
その単位の基底ベクトルを
に至った状況を現配置
と呼ぶ。
物体の状況とは関係無く,空間に固定した直角座標を定義し,
その単位の基底ベクトルを![]() (
(![]() , 2, 3)とする。
その基底ベクトルを初期配置において
物体に貼り付けた座標を埋め込み座標
と呼ぶことにし,その基底を埋め込み基底ベクトルと呼ぶが,
そのベクトルは物体に糊付けされているため,その変形に追随して変化する。
現配置におけるその基底ベクトルを
, 2, 3)とする。
その基底ベクトルを初期配置において
物体に貼り付けた座標を埋め込み座標
と呼ぶことにし,その基底を埋め込み基底ベクトルと呼ぶが,
そのベクトルは物体に糊付けされているため,その変形に追随して変化する。
現配置におけるその基底ベクトルを![]() (
(![]() , 2, 3)と
する。
, 2, 3)と
する。
![]() (
(![]() )である。
もちろん,図-12.1でも誇張したように,
埋め込み座標は一般には曲線座標であり直交系でもなく,
現配置の基底ベクトル
)である。
もちろん,図-12.1でも誇張したように,
埋め込み座標は一般には曲線座標であり直交系でもなく,
現配置の基底ベクトル![]() は単位基底にもならないことには十分注意する。
したがって埋め込み基底で定義されるテンソルの場合は,
その成分の扱いにおいて共変・反変成分の区別を正確に実施することや,
テンソル成分そのものは必ずしも物理的な量になっているとは
限らない12.3ことにも注意をして欲しい。
この
は単位基底にもならないことには十分注意する。
したがって埋め込み基底で定義されるテンソルの場合は,
その成分の扱いにおいて共変・反変成分の区別を正確に実施することや,
テンソル成分そのものは必ずしも物理的な量になっているとは
限らない12.3ことにも注意をして欲しい。
この![]() の定義が曖昧なまま以下に読み進むことは
やめておいた方がいい。怪我をします。
極座標での例を付録-Jに示しておいた。
一般的な定義とは異なりこの文書では,
あるテンソル量が定義される(測定される)配置を基準配置
と呼ぶことにする。
の定義が曖昧なまま以下に読み進むことは
やめておいた方がいい。怪我をします。
極座標での例を付録-Jに示しておいた。
一般的な定義とは異なりこの文書では,
あるテンソル量が定義される(測定される)配置を基準配置
と呼ぶことにする。
初期配置![]() における物体中の個々の点の位置
における物体中の個々の点の位置
![]() で
その点(物質点)
に「名前」を付けることにする。
ここで大文字の下添え字は,初期配置における点の関数,
つまり
で
その点(物質点)
に「名前」を付けることにする。
ここで大文字の下添え字は,初期配置における点の関数,
つまり![]() の関数として取り扱う場合に必要に応じて用いることにするが,
その定義は
の関数として取り扱う場合に必要に応じて用いることにするが,
その定義は
![]() ,
,
![]() (
(![]() )である。
さてその点が現配置
)である。
さてその点が現配置![]() において位置
において位置
![]() にあるものとする。
初期配置で名前を付けた点の現在の位置なので
にあるものとする。
初期配置で名前を付けた点の現在の位置なので![]() と
と![]() の
関数とみなしてある。以下しばらく時刻変数
の
関数とみなしてある。以下しばらく時刻変数![]() を省略するが,
最後まで勉強して復習するときには適宜自分で補ってみること。
逆に言えば,現配置に位置
を省略するが,
最後まで勉強して復習するときには適宜自分で補ってみること。
逆に言えば,現配置に位置![]() にある点の初期配置における
位置は,
にある点の初期配置における
位置は,
![]() のように現配置における位置の関数と
みなすこともできる。少々わかり難いとは思うが,単なる逆関係である。
また,この現配置の「位置ベクトル」を空間固定座標と同じ記号の
のように現配置における位置の関数と
みなすこともできる。少々わかり難いとは思うが,単なる逆関係である。
また,この現配置の「位置ベクトル」を空間固定座標と同じ記号の![]() で
表すことには,最初はとまどいがあると思うが慣れて欲しい。
頭の中では「現時点での位置ベクトル」だと思っている内に慣れると思う。
さて,いま着目した点の変位
で
表すことには,最初はとまどいがあると思うが慣れて欲しい。
頭の中では「現時点での位置ベクトル」だと思っている内に慣れると思う。
さて,いま着目した点の変位![]() は
この二つの位置の差で定義できるので
は
この二つの位置の差で定義できるので
と書くことができる。 最後の表現は,後述の式(12.15)のような逆関係が 唯一に存在することから用いることができる。 この変位で物体の運動12.4を 表現することができる。
次に変形を定義することを考えると,例えば任意の微分線要素の長さや
角度の変化等でそれは
定義できそうだ。そこでまず各配置における微分線要素ベクトルを成分で表すと
となる。もちろん総和規約を用いている。この第2式に偏微分の連鎖律を用いると
という関係が成立することがわかる。ここに![]() は変形勾配
と呼ばれる。
また添え字のコンマは
それに続く添え字に対応する変数による微分を表す。
式(12.1)の変位をこれに代入すると,この変形勾配は
は変形勾配
と呼ばれる。
また添え字のコンマは
それに続く添え字に対応する変数による微分を表す。
式(12.1)の変位をこれに代入すると,この変形勾配は
と書くこともできる。ここに![]() はKroneckerのデルタである。
ちなみに,上述の埋め込み座標の現配置の基底ベクトル
はKroneckerのデルタである。
ちなみに,上述の埋め込み座標の現配置の基底ベクトル![]() は
初期配置の
は
初期配置の![]() に貼り付けたベクトルであるから,
空間固定の基底ベクトルと
に貼り付けたベクトルであるから,
空間固定の基底ベクトルと
という関係にある。
あるいはこの式が![]() の定義だと考えてもいい。
の定義だと考えてもいい。
さて変形を表すために,
現配置におけるこの微分線要素の長さ![]() を求めておこう。すなわち
を求めておこう。すなわち
となることから,新しい量
![]() を
を
と定義する。
この
![]() は右Cauchy-Green変形テンソル
と呼ばれている。
上式(12.5)の微分要素が初期配置において持っていた長さも
同様に
は右Cauchy-Green変形テンソル
と呼ばれている。
上式(12.5)の微分要素が初期配置において持っていた長さも
同様に
と表すことができるので,その長さの変化で変形を定義することが可能である。
そのような変形の尺度として,Greenのひずみ
![]() を
を
と定義することにすると,
これに式(12.5)を代入して式(12.6)を使えば
という関係が成立する。ただし,![]() は2階の単位テンソル
(成分がKroneckerのデルタになる)である。
あるいは式(12.4)を用いて
は2階の単位テンソル
(成分がKroneckerのデルタになる)である。
あるいは式(12.4)を用いて
と定義しておくと,物理的な意味が少しは明らかになるかもしれない。
つまり,以上の誘導では微分線要素の長さのみに着目しているように見えるが,
この式(12.10)からは,物体に糊付けされた基底ベクトルの間の
変形前後の角度変形特性も,
基底ベクトル同士の内積を通してこのGreenのひずみ
![]() が
持っていることを示している。
さらに式(12.3)の変位表示の変形勾配を代入すれば
が
持っていることを示している。
さらに式(12.3)の変位表示の変形勾配を代入すれば
という関係になる。
有限変形を追跡しているので変位勾配の2次項が存在する。
この非線形項を無視すれば,微小変形理論のひずみの式(3.6)を得る。
このひずみは物体に初期配置において名前を付けた点を追跡するという
考え方,つまり初期に![]() にあった点が
にあった点が![]() の位置で
幾何学的・力学的に
どういう特性を持っているのか記述する,いわゆるLagrange的定式化
で表現したひずみである。
ちょうど,ひずみゲージを物体に貼り付けてそれを追跡した場合に
得られるひずみに相当する。
ただし,一般的なひずみゲージの測定値がこのGreenのひずみ成分であるわけではない。
の位置で
幾何学的・力学的に
どういう特性を持っているのか記述する,いわゆるLagrange的定式化
で表現したひずみである。
ちょうど,ひずみゲージを物体に貼り付けてそれを追跡した場合に
得られるひずみに相当する。
ただし,一般的なひずみゲージの測定値がこのGreenのひずみ成分であるわけではない。
ときどき使われるらしいが,変形の尺度にはならない`elongation'という
量がある。
と定義されるので,簡単に書くと
つまり変位勾配 である。これはもちろん剛体的な回転も含んでしまうので, 正確な変形の尺度にはならない。
最後に,現配置における体積![]() は,埋め込んだ基底ベクトルを用いれば
は,埋め込んだ基底ベクトルを用いれば
で定義できるから,式(12.4)を代入して整理すると
となる。ここに![]() は式(J.15)で定義した交代記号である。
つまり
は式(J.15)で定義した交代記号である。
つまり
と求められる。この![]() はJacobianと
呼ばれている。
初期配置と現配置における密度
をそれぞれ
はJacobianと
呼ばれている。
初期配置と現配置における密度
をそれぞれ![]() ,
, ![]() とすると,
質量保存則
から
とすると,
質量保存則
から
という関係も成立する。
したがって,普通の力学を対象とする限りは![]() は正値の非零で有界であることから,
変形勾配を行列にした場合にはその逆行列が唯一に存在する。
したがって,これもわかり難いとは思うが,現配置の位置が関数として
は正値の非零で有界であることから,
変形勾配を行列にした場合にはその逆行列が唯一に存在する。
したがって,これもわかり難いとは思うが,現配置の位置が関数として
と関係付けられる場合に,唯一にその逆の
という関係が定義できる12.6ことに
なる。![]() は
は![]() の
行列なので,その逆行列は
の
行列なので,その逆行列は
のように求めることができる。
この
![]() は
行列
は
行列![]() の余因子行列
である。
の余因子行列
である。
前節で求めた変形勾配や変位勾配には,
実際に物体が歪ゆがんでいる成分のみならず,
単に回転した成分も含まれていることには注意しなければいけない。
つまりまだ,材料の抵抗に深く関係する「歪ゆがみ」そのものを
きちんとは定義していないことになる。そこで,
変形勾配に含まれるかもしれない回転成分![]() については,
行列
については,
行列![]() で表現したときに
で表現したときに
のような特性で定義したとしても特に違和感は無いと思う。
ちょうど座標変換行列(正規直交行列)のようなものだ。
そこで,変形勾配を
と分解することを試みよう。このような分解を極分解の定理
と呼び,テンソル
![]() は対称テンソルであることがわかっている。
つまり
は対称テンソルであることがわかっている。
つまり![]() から
から![]() を取り除いた
成分の
を取り除いた
成分の![]() をいわゆる「歪ゆがみ」
つまり実質的な変形成分とみなそうというのである。
これを式(12.6)の変形テンソル
をいわゆる「歪ゆがみ」
つまり実質的な変形成分とみなそうというのである。
これを式(12.6)の変形テンソル![]() に代入すると
に代入すると
という関係が得られる。
すなわち変形テンソル![]() には回転成分は含まれていないことを示している。
したがって,式(12.9)のGreenのひずみテンソル
には回転成分は含まれていないことを示している。
したがって,式(12.9)のGreenのひずみテンソル![]() にも
回転は含まれていないことが期待できる。
この
にも
回転は含まれていないことが期待できる。
この![]() は右ストレッチテンソル
と呼ばれる。いわゆる伸びである。
は右ストレッチテンソル
と呼ばれる。いわゆる伸びである。
そこで,微小変形理論におけるひずみに主方向があったように,
この伸びにも主方向![]() と主ストレッチ
と主ストレッチ![]() が
あって,行列表示したときに
が
あって,行列表示したときに
と表現できるはずだ。
この![]() は単位ベクトルにすることができる。
また鈎括弧の
は単位ベクトルにすることができる。
また鈎括弧の
![]() は対角行列であることを示す。
行列
は対角行列であることを示す。
行列![]() は
正値実対称行列であることから,主値は正の実数であり,
主方向はお互いに直交するように選ぶことができる。
これを式(12.18)に代入すれば,行列表示で
は
正値実対称行列であることから,主値は正の実数であり,
主方向はお互いに直交するように選ぶことができる。
これを式(12.18)に代入すれば,行列表示で
となる。
![]() は
対角行列なので
は
対角行列なので
![]() は
対角成分が
は
対角成分が
![]() の行列である。このことから
の行列である。このことから
右ストレッチテンソル![]() は同じ主方向を持ち,
その主値は
は同じ主方向を持ち,
その主値は![]() になる。行列で書くと
になる。行列で書くと
となり,直接表記および行列表示にすると
というスペクトル表示 が可能になる。式(12.21)のような, テンソルおよび行列の平方根や2乗というのは,式(12.22)のような 関係にあるテンソルおよび行列であることを意味する。 実際にストレッチテンソルと回転成分を計算するには
ことになる。
ちなみに,Greenのひずみもスペクトル表示すると
となる。右ストレッチテンソル![]() に比べると,
変形テンソル
に比べると,
変形テンソル![]() やGreenのひずみテンソル
やGreenのひずみテンソル![]() の
物理的な意味はあまりよくわからない。
特に式(12.10)を見ると,例えば
の
物理的な意味はあまりよくわからない。
特に式(12.10)を見ると,例えば![]() と
と![]() は
必ずしも直交していない2方向の伸びの2乗に
なっているし,
は
必ずしも直交していない2方向の伸びの2乗に
なっているし,![]() は
は![]() と
と![]() の長さの伸びも
含んでしまっている。
これでは,この
の長さの伸びも
含んでしまっている。
これでは,この![]() をそのまま構成則に用いることには大きな抵抗を
感じざるを得ない。
つまり何らかの物理成分,例えば
をそのまま構成則に用いることには大きな抵抗を
感じざるを得ない。
つまり何らかの物理成分,例えば
(12.24)
のような成分の方がいいように感じるがどうだろう。
回転を定義するときに,式(12.17)とは逆の順序にしてもいいだろう。
つまり
のようにも極分解できる。
これを式(12.6)の変形テンソル![]() に代入すると
に代入すると
という関係が得られる。
あるいは上式に左右から回転を乗ずると
となることから,![]() も実質的な変形である可能性がある。
も実質的な変形である可能性がある。
そこで,式(12.7)の![]() を
式(12.15)の逆関係を用いて表すと
を
式(12.15)の逆関係を用いて表すと
となるので,
この
![]() の部分に極分解式(12.25)を代入すると
の部分に極分解式(12.25)を代入すると
となり式(12.26)で定義した![]() になっていることがわかる。
すなわち
になっていることがわかる。
すなわち
という関係が求められる。
この
![]() は
は
![]() と
対峙させて左Cauchy-Green変形テンソル
と呼ばれ,
と
対峙させて左Cauchy-Green変形テンソル
と呼ばれ,
![]() も
も
![]() に
対峙させて左ストレッチテンソル
と呼ばれている。
面白いことに,
に
対峙させて左ストレッチテンソル
と呼ばれている。
面白いことに,![]() と
と![]() の主値(固有値)同士は
同じになるので,
式(12.22)と同様,次のようなスペクトル表示ができる。
の主値(固有値)同士は
同じになるので,
式(12.22)と同様,次のようなスペクトル表示ができる。
ただし
であり,主方向の![]() と
と![]() の間には
の間には
という関係が成立する。つまり,主方向![]() は,現配置において空間固定座標のどの方向に
主に伸びているのかを表すベクトルであり,これに対して
主方向
は,現配置において空間固定座標のどの方向に
主に伸びているのかを表すベクトルであり,これに対して
主方向![]() は,その現配置で主に伸びている方向が
初期配置でどちらを向いていたか(材料に貼り付けた埋め込み座標で
表現した主に伸びている方向)を示している。
ところで,定義から
は,その現配置で主に伸びている方向が
初期配置でどちらを向いていたか(材料に貼り付けた埋め込み座標で
表現した主に伸びている方向)を示している。
ところで,定義から
という関係が成り立つ。
最後に式(12.8)のGreenのひずみに
対峙させたひずみ
![]() を
を
と定義すると,これに式(12.27)を代入して,
さらに変位を用いた関係
を代入して整理すると
という関係を得る。
このひずみ
![]() をAlmansiのひずみ
と呼ぶ。注意しないといけないのは,変位を現配置の「位置」
をAlmansiのひずみ
と呼ぶ。注意しないといけないのは,変位を現配置の「位置」![]() の
関数として取り扱っていることと,
空間固定座標で微分をしていることの二つだ。
これは,初期配置で名前を付けた点を追跡するという記述ではなく,
空間のある場所を観察しているときに,その観察点で何が起こっているか
ということを観察する手法,いわゆるEuler的定式化
による記述になっている。
例えば透明な壁を持つ水路の中の流体の運動を,
その水槽の壁面に付けた印の場所で定点カメラによって観察する場合のように,
モニターしている観察点で起こっている現象を対象とする場合には,
このEuler的定式化の方が便利である。
固体の場合も,非接触型の変位計やひずみ計を用いて現象を観測するならEuler的な
観察をしていることになるが,普通はEuler的な手法はあまり馴染まない。
流体の場合も,一緒に運動するマーカーを投げ入れてそれを
追跡する場合にはLagrange的な方法を用いて何かを測定していることになる。
の
関数として取り扱っていることと,
空間固定座標で微分をしていることの二つだ。
これは,初期配置で名前を付けた点を追跡するという記述ではなく,
空間のある場所を観察しているときに,その観察点で何が起こっているか
ということを観察する手法,いわゆるEuler的定式化
による記述になっている。
例えば透明な壁を持つ水路の中の流体の運動を,
その水槽の壁面に付けた印の場所で定点カメラによって観察する場合のように,
モニターしている観察点で起こっている現象を対象とする場合には,
このEuler的定式化の方が便利である。
固体の場合も,非接触型の変位計やひずみ計を用いて現象を観測するならEuler的な
観察をしていることになるが,普通はEuler的な手法はあまり馴染まない。
流体の場合も,一緒に運動するマーカーを投げ入れてそれを
追跡する場合にはLagrange的な方法を用いて何かを測定していることになる。
簡単な例で物理的な意味を確かめておこう。図-12.2の左に示した
運動は3軸方向へのストレッチ![]() と
と![]() -
-![]() 面内の回転のみの
簡単な運動なので,少し考えれば
面内の回転のみの
簡単な運動なので,少し考えれば
となることがわかる。つまり
という極分解ができることを示している。![]() は
対角行列であるから,特に固有値解析をするまでもなく,
主値は
は
対角行列であるから,特に固有値解析をするまでもなく,
主値は
![]() であり,それぞれの主方向は
であり,それぞれの主方向は
と求められる。
つまり,初期配置における材料の![]() 方向に主ストレッチが生じている,
あるいは材料に埋め込んだ
座標の
方向に主ストレッチが生じている,
あるいは材料に埋め込んだ
座標の
![]() 方向に主に伸びていると
考えればいい。
これを式(12.31)に代入すれば
方向に主に伸びていると
考えればいい。
これを式(12.31)に代入すれば
を得る。これは図からも明らかように,三つの伸び![]() が現配置で
生じている方向を空間固定座標系から見たのが
が現配置で
生じている方向を空間固定座標系から見たのが![]() であることがわかる。
この主方向と三つの主値を式(12.29)に代入するか,
あるいは二つのストレッチ間の関係式(12.32)を用いれば,
左ストレッチテンソルが
であることがわかる。
この主方向と三つの主値を式(12.29)に代入するか,
あるいは二つのストレッチ間の関係式(12.32)を用いれば,
左ストレッチテンソルが
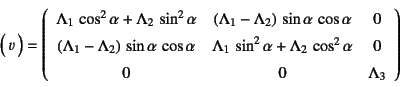
と求められる。
この2種類のストレッチテンソルの物理的な意味を図-12.2の
右に示しておいた。
先に回転させるか,あとで回転させるかの違いで,2種類の
ストレッチテンソルが定義されていることがわかる。
つまり,先に回転させた物体の基底![]() の系の「方向」の成分を
持つ実質的な変形が
の系の「方向」の成分を
持つ実質的な変形が![]() になっている。
になっている。
ついでにGreenのひずみを求めておこう。
式(12.34)から変位勾配は

となるので,式(12.11)に代入すれば,
せん断ひずみ成分は零になり
と求めることができる。
もちろん,式(12.23)のスペクトル表示に
式(12.35)の主ストレッチと式(12.36)のLagrange的
主方向を代入しても,同じ表現を得る。
式(12.23)のスペクトル表示からもわかるように,
伸びの2乗に関係付けられているので物理的な意味はわかり難い。
ただし,どちらの向きあるいはどの座標軸における変形であるかについては,
この例はわかり易い。つまり,式(12.23)に用いた
基底![]() の通り,材料に貼り付けた
の通り,材料に貼り付けた![]() 方向の伸び,
すなわち埋め込み基底を
単位量にした
方向の伸び,
すなわち埋め込み基底を
単位量にした
![]() 方向の
伸びに関係した量である。
物体に貼り付けたひずみゲージの測定値のように,
物体の上で測定しているひずみになっている。
したがって,特に内部に微視構造を持つ異方性材料の構成則には,
このようなLagrange的な尺度の方が適していることがわかる。
実は,節-E.2で定式化したBernoulli-Euler梁の
定式化では,Greenのひずみを用いて非常に美しい理論が構築できている。
ただそこでは,Greenのひずみテンソルの成分そのものではなく,それに対応した
物理的な成分が用いられているからである。
仮想仕事の原理を通して,数学的にも物理的にも説得力のある理論になっている。
これについては,後述の応力の物理成分の節で簡単に解説しよう。
方向の
伸びに関係した量である。
物体に貼り付けたひずみゲージの測定値のように,
物体の上で測定しているひずみになっている。
したがって,特に内部に微視構造を持つ異方性材料の構成則には,
このようなLagrange的な尺度の方が適していることがわかる。
実は,節-E.2で定式化したBernoulli-Euler梁の
定式化では,Greenのひずみを用いて非常に美しい理論が構築できている。
ただそこでは,Greenのひずみテンソルの成分そのものではなく,それに対応した
物理的な成分が用いられているからである。
仮想仕事の原理を通して,数学的にも物理的にも説得力のある理論になっている。
これについては,後述の応力の物理成分の節で簡単に解説しよう。
前節では単なる幾何学的な考察で,理論的な変形の尺度とひずみや回転を定義した。
しかし,実際に材料が直に感じる(材料はしゃべらないので,
我々が直感的・物理的12.7に
合理的だと感ずる)実質的な「歪み」,
つまり「ひずみ」はどう定義するのがいいのだろう。
少なくともそれは,変形テンソル![]() でもGreenのひずみテンソル
でもGreenのひずみテンソル![]() でも
なさそうだ。
そこで図-12.3にあるように,
でも
なさそうだ。
そこで図-12.3にあるように,![]() の正方形が
回転成分を持たないまま,
の正方形が
回転成分を持たないまま,![]() の角度変化と2辺が同じ比率で
伸びて
の角度変化と2辺が同じ比率で
伸びて![]() になっている状態を対象として,いくつか歪みを定義してみよう。
まず,この変形状態は
になっている状態を対象として,いくつか歪みを定義してみよう。
まず,この変形状態は
となることは容易にわかると思う。![]() と
と![]() を独立した変形指標とした
純せん断状態なので,かなり限定的な純せん断状態になっていることには注意する。
ただし,
を独立した変形指標とした
純せん断状態なので,かなり限定的な純せん断状態になっていることには注意する。
ただし,![]() は図には無いが,
は図には無いが,![]() 方向の伸びである。
回転成分を除去したような変形状態を
対象としていることから,
方向の伸びである。
回転成分を除去したような変形状態を
対象としていることから,
![]() であり,
変形勾配と二つのストレッチテンソルには違いが無い。
このとき主値と主方向を求めるために
であり,
変形勾配と二つのストレッチテンソルには違いが無い。
このとき主値と主方向を求めるために![]() の固有値解析をすると
の固有値解析をすると
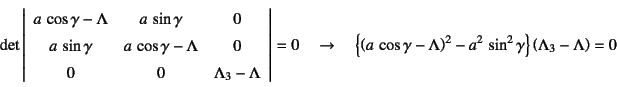
となるので,これを解くと,主ストレッチが
と求められ,対応する主方向は
となる。
すなわち,![]() 軸から反時計回りの45度方向に伸び
軸から反時計回りの45度方向に伸び![]() が
生じ,時計回りの45度方向に伸び
が
生じ,時計回りの45度方向に伸び![]() が生じている。
そしてこの二つの長さ
が生じている。
そしてこの二つの長さ![]() ,
, ![]() は,
とりもなおさずこのひし形の対角線の長さに等しい。
このようにストレッチ
は,
とりもなおさずこのひし形の対角線の長さに等しい。
このようにストレッチ![]() と角度変化
と角度変化![]() は
幾何学的・物理的に非常にわかり易い変形量である。
は
幾何学的・物理的に非常にわかり易い変形量である。
まず伸びについては,よく引張り試験の標点間距離で定義する
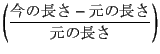 と
いう定義は比較的誰にでも受け入れられるのではないだろうか。
つまり,その伸びひずみ
と
いう定義は比較的誰にでも受け入れられるのではないだろうか。
つまり,その伸びひずみ![]() を,この図の例では
を,この図の例では
と定義すれば,これが辺の伸びになるだろう。
この定義は![]() のときの主ストレッチから元の長さ1を
引いた,いわゆる伸びになっている。
これを用いると,引張りの100%のひずみ(
のときの主ストレッチから元の長さ1を
引いた,いわゆる伸びになっている。
これを用いると,引張りの100%のひずみ(![]() )は
)は![]() (長さが
元の倍)で生じるのでよさそうではあるが,
実は縮みの100% (
(長さが
元の倍)で生じるのでよさそうではあるが,
実は縮みの100% (![]() )は物体の消滅(
)は物体の消滅(![]() )に
一致してしまうという問題がある。
そこで,構成則の研究でよく使われる対数ひずみ
)に
一致してしまうという問題がある。
そこで,構成則の研究でよく使われる対数ひずみ![]() を
を
のように定義してみよう。
こうすると,伸びの100%である![]() が
が
![]() で,
縮みの100% (
で,
縮みの100% (![]() )が
)が
![]() となる。
対数に自然対数を用いているので,長さが2.72倍で100%の伸びに
なり,
となる。
対数に自然対数を用いているので,長さが2.72倍で100%の伸びに
なり,
![]() に縮んだときに100%の縮みになっている。
逆に考えると長さが倍か半分になったときの
対数ひずみは
に縮んだときに100%の縮みになっている。
逆に考えると長さが倍か半分になったときの
対数ひずみは
![]() %である。
もし底が2の対数
%である。
もし底が2の対数![]() を用いれば,長さが倍になるのが伸びの100%の
ひずみであり,長さが半分になるのが縮みの100%の変形であるから,
直感的に受け入れられるような気もするが,
縮みはちょっとだけ気になるかなぁ。
を用いれば,長さが倍になるのが伸びの100%の
ひずみであり,長さが半分になるのが縮みの100%の変形であるから,
直感的に受け入れられるような気もするが,
縮みはちょっとだけ気になるかなぁ。
さて,テンソルとしてはGreenのひずみがよく用いられている
ひずみの尺度の一つのようであるが,その物理的な意味はよくわからない。
これに対して,
ここで導入した伸びひずみや対数ひずみはわかり易い変形の尺度ではないだろうか。
そこで,式(12.42) (12.43)を見ながら
で,伸びひずみテンソル
と対数ひずみテンソルを定義しておこう。
この伸びひずみ
![]() は,
変形の尺度には相応しくないとした
変位勾配(`elongation')の式(12.12)に
似ているが,
は,
変形の尺度には相応しくないとした
変位勾配(`elongation')の式(12.12)に
似ているが,![]() で定義することによって回転成分は除去されている。
スペクトル表示すると
で定義することによって回転成分は除去されている。
スペクトル表示すると
と書くことができる。このひずみはBiotのひずみテンソル
と呼ばれることもある。
また,対数ひずみテンソル
![]() は
スペクトル表示を用いて
は
スペクトル表示を用いて
で定義できる。式(12.39) (12.40)
(12.41)を用いて,この二つのひずみを![]() -
-![]() 面
内成分だけを求めておくと
面
内成分だけを求めておくと
となる。純せん断状態なのに,伸びひずみのせん断成分![]() には
伸び
には
伸び![]() が含まれてしまっている。
これに対し対数ひずみのせん断成分は,純せん断であることを
反映して角度変化のみで表すことができている。
一方,前節のLagrange的定式化で定義した
式(12.9)のGreenのひずみ
が含まれてしまっている。
これに対し対数ひずみのせん断成分は,純せん断であることを
反映して角度変化のみで表すことができている。
一方,前節のLagrange的定式化で定義した
式(12.9)のGreenのひずみ![]() は
は
となる。Lagrange的定式化では最もよく用いられると思われる
ひずみであるが,伸びの100%である![]() は
は
![]() に
対応するが,縮みの100% (
に
対応するが,縮みの100% (![]() )は
)は![]() !!!を要請してしまうことになる。
また元々変形前後の長さの2乗の変化で定義したひずみであることから,
伸び
!!!を要請してしまうことになる。
また元々変形前後の長さの2乗の変化で定義したひずみであることから,
伸び![]() の2乗が含まれる上に,
上記の伸びひずみと同様に,純せん断状態でもせん断ひずみ成分
の2乗が含まれる上に,
上記の伸びひずみと同様に,純せん断状態でもせん断ひずみ成分![]() に
伸び
に
伸び![]() が含まれてしまっている。
が含まれてしまっている。
前節の例も含め,図-12.2と図-12.3の 例で実際に求めたひずみの成分式(12.35) (12.38) (12.39) (12.47) (12.48)を 幾何学的に解釈してみると
と考えればいいだろう。 すべて数学的に誘導されたひずみであり,必ずしも材料試験で 測定できるひずみになっているとは限らないことには注意すべきだ。 前述のように,特に固体を対象とする場合には,その物体に ひずみゲージを貼り付けて測定することがある。 これはまさにLagrange的な量を測定していることから,この四つ すべてが変形の尺度としては相応しいものと考えて 問題は無さそうだ。ただしGreenのひずみの 場合は,ここの例からもわかるように, その成分の物理的な意味は非常にわかり難い。
図-12.4には,
横軸に辺の伸びひずみ![]() を用いた場合と,
対数ひずみ
を用いた場合と,
対数ひずみ![]() を用いた場合の,3種類のひずみテンソルの11成分を比較した。
ただし,
を用いた場合の,3種類のひずみテンソルの11成分を比較した。
ただし,![]() と
と
![]() は式(12.47)で
は式(12.47)で![]() のときの値を用いている。
横軸はどちらも長さが倍か半分になるまでの範囲で描いてみた。
もちろん図-12.4(a)では,定義が横軸と同じ
のときの値を用いている。
横軸はどちらも長さが倍か半分になるまでの範囲で描いてみた。
もちろん図-12.4(a)では,定義が横軸と同じ![]() が
直線関係にあり,図-12.4(b)でも,
定義が横軸と同じ
が
直線関係にあり,図-12.4(b)でも,
定義が横軸と同じ![]() が直線関係になっている。
当然ではあるが,ひずみが微小でありさえすれば,どの尺度を
用いても,少なくとも工学的には差異は生じない。
実際に100%を超えるような有限変形問題を対象とする場合に,
どの尺度が望ましいか,なかなか判断は難しい。
が直線関係になっている。
当然ではあるが,ひずみが微小でありさえすれば,どの尺度を
用いても,少なくとも工学的には差異は生じない。
実際に100%を超えるような有限変形問題を対象とする場合に,
どの尺度が望ましいか,なかなか判断は難しい。
次にせん断ひずみについて同様の比較をしてみよう。
図-12.5には,
横軸には角度変化![]() を
を![]() で割ったものを用いて,3種類の
せん断ひずみテンソル成分を比較した。
ただし,
で割ったものを用いて,3種類の
せん断ひずみテンソル成分を比較した。
ただし,![]() と
と![]() は式(12.47)
(12.48)で
は式(12.47)
(12.48)で![]() のときの値を用いている。
これも当然ではあるが,ひずみが微小でありさえすれば,どの尺度を
用いても,少なくとも工学的には差異は生じない。
しかし,対数ひずみだけが角度の増加に伴って急速に無限大に近づくような
挙動をしており,奇妙に思える。
しかし本当にそうだろうか。
この横軸は実は
のときの値を用いている。
これも当然ではあるが,ひずみが微小でありさえすれば,どの尺度を
用いても,少なくとも工学的には差異は生じない。
しかし,対数ひずみだけが角度の増加に伴って急速に無限大に近づくような
挙動をしており,奇妙に思える。
しかし本当にそうだろうか。
この横軸は実は
![]() の範囲で
描いてあるのだが,
の範囲で
描いてあるのだが,![]() が
が
![]() に
近づくということは物体が消滅することを意味する。
それは質量保存則からは許容できる状態ではない。
したがって,
に
近づくということは物体が消滅することを意味する。
それは質量保存則からは許容できる状態ではない。
したがって,
![]() でせん断ひずみの
尺度そのものは無限大になるべきなのである。
また対数ひずみは式(12.47)でも示したように,
純せん断を純粋に角度変化
でせん断ひずみの
尺度そのものは無限大になるべきなのである。
また対数ひずみは式(12.47)でも示したように,
純せん断を純粋に角度変化![]() のみで表現できていることからも,
優れた尺度であると考えられる。
これに対し伸びひずみとGreenのひずみは,
のみで表現できていることからも,
優れた尺度であると考えられる。
これに対し伸びひずみとGreenのひずみは,
![]() の
状態で有界な値を保持している。
だからこの二つは有限変形を記述するのには相応しくないと言うことが
できるだろうか。
上述のようにこの2種類のせん断ひずみ成分は,実際には辺の伸び
の
状態で有界な値を保持している。
だからこの二つは有限変形を記述するのには相応しくないと言うことが
できるだろうか。
上述のようにこの2種類のせん断ひずみ成分は,実際には辺の伸び![]() が
含まれており,実はこの図では
が
含まれており,実はこの図では![]() と固定していることから,
不適切とも思える結果が表示されたに過ぎない。
実際には構成則を介して,
と固定していることから,
不適切とも思える結果が表示されたに過ぎない。
実際には構成則を介して,![]() の増大に伴って
の増大に伴って![]() や
や![]() が
無限大になることによって,このせん断ひずみ成分も無限大になることになる。
つまり逆に言うと,もし構成則に使いたいなら,伸びひずみとGreenのひずみの
せん断成分には伸び
が
無限大になることによって,このせん断ひずみ成分も無限大になることになる。
つまり逆に言うと,もし構成則に使いたいなら,伸びひずみとGreenのひずみの
せん断成分には伸び![]() が含まれているのが当たり前だったということを意味する。
これは,式(12.23)のすぐ下に書いたコメントとは矛盾しているので
注意が必要だ。
ただし
が含まれているのが当たり前だったということを意味する。
これは,式(12.23)のすぐ下に書いたコメントとは矛盾しているので
注意が必要だ。
ただし![]() を一定と考えたとき,
を一定と考えたとき,![]() (
(![]() )にしろ
)にしろ![]() にしろ,
それぞれ
にしろ,
それぞれ![]() あるいは
あるいは![]() であることから,
角度が
であることから,
角度が
![]() あるいは
あるいは
![]() でピークを持つ
周期関数になっていることも若干気になるところではある。
でピークを持つ
周期関数になっていることも若干気になるところではある。
では伸びについての対数ひずみの検討に戻ろう。
式(12.43)のスカラーで定義した対数ひずみを
一般化した対数ひずみの定義式(12.46)を見ながら,
この変化率を計算してみよう。
次の節で議論する「ひずみ速度」を少しここで求めてみようというのである。
簡単のために![]() 方向にのみ
方向にのみ![]() が生じている状況を
対象としてみると,対数ひずみは
が生じている状況を
対象としてみると,対数ひずみは![]() でいい。
この変化率は
でいい。
この変化率は
と書くことができる。簡単のために時間微分を上付きドットで表した。
この![]() は初期配置の長さに対する現配置の長さの比で
あることから,初期配置の長さを
は初期配置の長さに対する現配置の長さの比で
あることから,初期配置の長さを![]() として現配置の長さを
として現配置の長さを![]() と置くと
と置くと
となる。
つまり対数ひずみの変化率は,現配置を基準配置としたときの瞬間的なLagrange的な
長さの変化率を示していることになる。
これはちょうど,現配置を時々刻々初期配置と捉えて定式化するupdated
Lagrange的定式化(p.![]() )において
最も使い易い変形の尺度になりそうだ。
また,変形が大きくなった場合に多くの材料が示す塑性の基本的なモデルでは,
流れ則という発展則で材料特性を表すことになっているが,
この流れ則は現配置の応力状態で瞬間的にのみ定義されている。
また発展則は増分式あるいは全微分表現で定義され,一般には積分不可能である。
この2点を踏まえると,塑性の発展則ではupdated Lagrange的な増分を
規定していることになる。
このような観点でひずみの定義を検討してみると,
ここで定義した対数ひずみは,
特に,塑性を伴う有限変形問題では最も相応しい尺度の代表であると考えられる。
また実験の観点から見ても,初期配置を覚えておかなくてもいいので
測定し易い指標になっているが,ひずみゲージが測定している量と一対一に
対応しているわけではない。
また,瞬間的にはいつも空間固定座標方向の成分で表現しようとすることから,
材料の内部微視構造が変化するような材料では,使い難い尺度かもしれない。
いいものはなかなか簡単には手に入らないということだ。
)において
最も使い易い変形の尺度になりそうだ。
また,変形が大きくなった場合に多くの材料が示す塑性の基本的なモデルでは,
流れ則という発展則で材料特性を表すことになっているが,
この流れ則は現配置の応力状態で瞬間的にのみ定義されている。
また発展則は増分式あるいは全微分表現で定義され,一般には積分不可能である。
この2点を踏まえると,塑性の発展則ではupdated Lagrange的な増分を
規定していることになる。
このような観点でひずみの定義を検討してみると,
ここで定義した対数ひずみは,
特に,塑性を伴う有限変形問題では最も相応しい尺度の代表であると考えられる。
また実験の観点から見ても,初期配置を覚えておかなくてもいいので
測定し易い指標になっているが,ひずみゲージが測定している量と一対一に
対応しているわけではない。
また,瞬間的にはいつも空間固定座標方向の成分で表現しようとすることから,
材料の内部微視構造が変化するような材料では,使い難い尺度かもしれない。
いいものはなかなか簡単には手に入らないということだ。
さて,Greenのひずみの場合はどうだろう。
同じように1軸方向の変形しか無い状態におけるGreenのひずみの
変化率を求めてみよう。式(12.2)
(12.6) (12.9)を用いると
となるが,速度![]() を
を
と成分表示をすると
と書くことができる。これを上式に代入して整理すると
という関係を得る。この![]() は次の節で定義する変形速度である。
この式に,1方向にのみ伸びている状況では
は次の節で定義する変形速度である。
この式に,1方向にのみ伸びている状況では
![]() となっている
ことを代入し,
式(12.38)のGreenのひずみ成分
となっている
ことを代入し,
式(12.38)のGreenのひずみ成分![]() が
が
![]() であることを用いてその変化率をとると
であることを用いてその変化率をとると
という関係が求められる。つまり,概念的には上式(![]() )と比較すれば
)と比較すれば
のように,変形速度つまりGreenのひずみの変化率は
対数ひずみの時間変化率と同じような量であることがわかる。
構成則で対数ひずみを直接扱おうとすると,変位との関係で常に極分解を
介さなければならない難点があるが,増分で構成則を表さざるを得ない
塑性を含めた構成則においては,この変形速度を用いて増分理論を
定式化しておけば,それは結局,
対数ひずみで物体の変形を表現しようとしていることになることが,
この簡単な例からわかる。
そのため,塑性を含む構成則の研究においてはupdated Lagrange的
定式化が必然であり,かつ構成則を増分で表すというのは,
有限変形におけるひずみの物理的な定義の観点からも必然なのだろう。
ただし,もしどうしてもLagrange的定式化で構成則を表現する必要が
あるとすれば,著者の気持ちとしては,ある適切に定義された
応力
![]() を用いて(
を用いて(
![]() は
後述のCauchy応力
は
後述のCauchy応力
![]() とは限らない)
とは限らない)
が望ましいような気がする。
ここに![]() は何らかの材料の抵抗を定義する4階の
材料パラメータテンソルであるが,一般には定数とは限らない。
定数パラメータの場合の
いくつかの例については,節-12.5.3に示す。
は何らかの材料の抵抗を定義する4階の
材料パラメータテンソルであるが,一般には定数とは限らない。
定数パラメータの場合の
いくつかの例については,節-12.5.3に示す。
有限変形する材料のほとんどが示す塑性における流れ則の基本は,
ひずみの増分あるいは変化率・速度が応力と平行・共軸になるというものだった。
したがって,このひずみ増分を有限変形の枠組の中でも適切に
定義しておく必要がある。
しかもそのひずみ増分は,
ある現配置における瞬間的な増分で表されることから,Euler的な
変化率12.8を
ここでは求めておこう。
まず,ある物質点![]() が現配置で持っている速度
が現配置で持っている速度
![]() は
は
と定義できる。上付きドットは時間(配置あるいは変形履歴)による微分を表す。
したがって変形勾配の変化率は
という関係がある。
次に,式(12.9)のGreenのひずみの変化率は
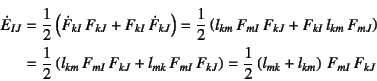
となることから
と表すことができる。この
![]() は変形速度
と呼ばれ,ひずみ速度の代表的な量である。
これはちょうど式(3.6)で定義した微小変形理論のひずみの
速度版のように見えることから,この増分で表した定式化を微小変形理論だと
誤解する人もいるので注意しなければならない。
上式では,量は現配置
は変形速度
と呼ばれ,ひずみ速度の代表的な量である。
これはちょうど式(3.6)で定義した微小変形理論のひずみの
速度版のように見えることから,この増分で表した定式化を微小変形理論だと
誤解する人もいるので注意しなければならない。
上式では,量は現配置![]() で定義されている上に,
微分も空間固定座標あるいは現位置でとられていることに注意すべきである。
詳細は後述するが,少し乱暴に,例えば
で定義されている上に,
微分も空間固定座標あるいは現位置でとられていることに注意すべきである。
詳細は後述するが,少し乱暴に,例えば![]() を具体的に書くと
を具体的に書くと
と解釈できることから,前節の最後に解説したように, 変形速度は対数ひずみの変化率に相当していることがわかる。 正確な対数ひずみ速度はあとで定義する。
これに対し,スピンも定義しておく必要がありそうだ。まずは
前節の極分解の定理式(12.17)で得られた![]() が
運動に含まれる回転成分を定義しているので,
その時間変化率でスピンを定義することができる。つまり
が
運動に含まれる回転成分を定義しているので,
その時間変化率でスピンを定義することができる。つまり
のような
![]() は,スピンの尺度の代表になる。
あるいは変形の主方向の変化,つまり
は,スピンの尺度の代表になる。
あるいは変形の主方向の変化,つまり![]() や
や![]() の
主方向の
の
主方向の![]() や
や![]() の変化率で
の変化率で
のような
![]() や
や
![]() で
スピン12.9を
定義[59]することもできる。
このように定義すると,式(12.31)から
で
スピン12.9を
定義[59]することもできる。
このように定義すると,式(12.31)から
となることから,右から
![]() を乗じて
を乗じて
という関係を得る。
しかしここでは,上式(12.52)の変形速度に対応したスピンも
定義しておこう。
それは現配置で考える以上,通常の回転ベクトル![]() の
成分として考えればいいので
の
成分として考えればいいので
で回転が定義できる。ただし,この式中の下線の付いた指標に
対しては総和規約を適用せず,かつ,![]() ,
, ![]() ,
, ![]() である。
この回転ベクトルの成分からの類推により
である。
この回転ベクトルの成分からの類推により
で最も基本的なスピン
を定義する。このスピン
![]() の定義では,
添え字の順番が逆になっている文献もあるので注意する。
このように定義しておけば,速度勾配との間には
の定義では,
添え字の順番が逆になっている文献もあるので注意する。
このように定義しておけば,速度勾配との間には
と関係付けることができ,変形速度![]() とスピン
とスピン![]() は
それぞれ速度勾配
は
それぞれ速度勾配![]() の対称成分と反対称成分
になる。
の対称成分と反対称成分
になる。
さて,式(12.13)の体積変化の変化率も求めておこう。 単に時間微分をとることによって
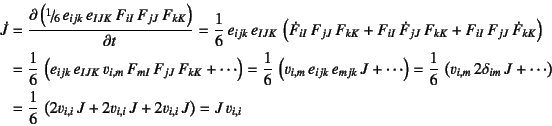
となるので
という関係がある。
これから密度の変化則を求めるために,式(12.14)の時間微分をとり,
上式(12.58)を代入すると
となる。質量保存則のもう一つの表現である。
ちなみにこのことから,
完全流体のように体積が変化できない材料の非圧縮性
の条件は
となり,流体力学の世界では何故かこれが連続の式 と呼ばれている。
最後に,運動方程式に現れる慣性項の加速度
を定義しておこう。
加速度
![]() は速度の変化率であるから,単純に
は速度の変化率であるから,単純に
であることには間違い無いが,慣性項に使われる加速度は
物体のある「物質点」![]() が持っている加速度でなければならない。
つまり
が持っている加速度でなければならない。
つまり![]() の関数として定義された速度の変化率でなければならない。
上の式に書いたように,
の関数として定義された速度の変化率でなければならない。
上の式に書いたように,![]() は「場所」
は「場所」![]() の関数として
取り扱うものの,この位置
の関数として
取り扱うものの,この位置![]() そのものも,
ある物体の「物質点」と時間の関数
そのものも,
ある物体の「物質点」と時間の関数
![]() になるため,
いわゆる連鎖律
によって,次のような演算が必要になってくる。
になるため,
いわゆる連鎖律
によって,次のような演算が必要になってくる。
つまり上付きのドットは,実はある物体の「物質点」を
追跡した場合の時間変化率の算定になっており
の微分操作を物質微分
と呼び,その変化率を物質微係数
(物質導関数)と呼んでいる。
第2項は,流体力学(水理学)で習うNavier-Stokesの式にも
現れる重要な項であり,移流項
と呼ばれている。
このように,Euler的な量の時間変化率を算定する場合には注意が必要である。
この節の始めにEuler的な定式化と書いたが,確かに「場所」![]() の
関数としての量を取り扱ってはいるものの,実際には(固体の)連続体の力学なので,
実は物体の「物質点」
の
関数としての量を取り扱ってはいるものの,実際には(固体の)連続体の力学なので,
実は物体の「物質点」![]() を追跡していることには常に注意が必要だ。
を追跡していることには常に注意が必要だ。
変形の変化率・速度は初学者にとってはその物理的な意味がわかり難い ものである。 また特にスピンには複数の定義があったことから, まずは具体的な例を用いて物理的な考察をしておこう。
最初は図-12.2の例で変化率を求めてみよう。
まず式(12.35)の![]() を時間微分すれば
を時間微分すれば
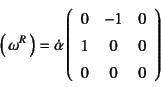
と求められる。同様に式(12.37)の![]() の時間微分から
の時間微分から
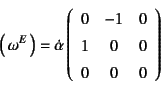
となる。これは上式の
![]() と一致する。
そのため,式(12.55)に代入すれば
と一致する。
そのため,式(12.55)に代入すれば![]() を得るが,
それは,式(12.36)の
を得るが,
それは,式(12.36)の![]() が定数であることからも
求められる。
この例は,例えば初期配置において
が定数であることからも
求められる。
この例は,例えば初期配置において![]() ,
, ![]() 方向に直交する繊維の
向きを合わせた布だと想定すると,その後の変形においては,
確かに
方向に直交する繊維の
向きを合わせた布だと想定すると,その後の変形においては,
確かに![]() で回転してはいるものの,布にとっては
常にそのそれぞれの繊維がお互いに直交し,
その繊維方向にだけ伸び縮みさせられている状態にある。
つまり,材料にとっては変形の向きが変わったようには感じないのである。
このように,この
で回転してはいるものの,布にとっては
常にそのそれぞれの繊維がお互いに直交し,
その繊維方向にだけ伸び縮みさせられている状態にある。
つまり,材料にとっては変形の向きが変わったようには感じないのである。
このように,この![]() は物体と一緒に回転している立場から見た
変形状態のスピンであるから,零になっている。
は物体と一緒に回転している立場から見た
変形状態のスピンであるから,零になっている。
次に式(12.34)の変形勾配![]() を時間微分することによって,
速度勾配が
を時間微分することによって,
速度勾配が
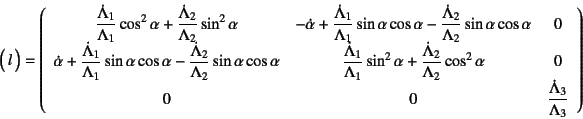
と求められる。これを式(12.52)に代入すれば
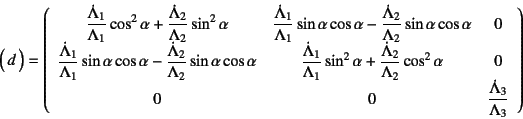
となるが,実はこれをよく眺めると
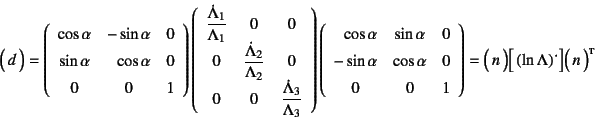
という関係にあることがわかる。
つまりEuler的(否,後述のupdated Lagrange的)に見た,
ある場所の対数ひずみ速度に相当する。
つまり,Euler的な主方向(図-12.2の変形後の
直方体の各辺の方向)に対数ひずみ速度で
単純に伸び変形しつつある状態であることがわかる。
一方,式(12.56)に速度勾配を代入すれば
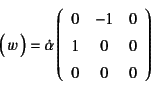
と求められる。これは先に求めた
![]() ,
,
![]() に一致する。
どちらに近いスピンなのかについては後述する。
物理的には
に一致する。
どちらに近いスピンなのかについては後述する。
物理的には![]() の速度で回転していることが明らかである。
の速度で回転していることが明らかである。
次に図-12.3の例で計算しておこう。
まず,これは非回転運動であることは明らかであり
となる。
次に式(12.34)の変形勾配![]() を時間微分することによって,
速度勾配が求められ,それを式(12.52)に代入すれば変形速度が
求められる。この例では回転していないので,それは一致し
を時間微分することによって,
速度勾配が求められ,それを式(12.52)に代入すれば変形速度が
求められる。この例では回転していないので,それは一致し
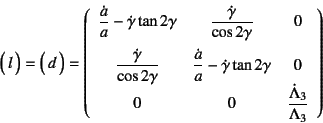
と求められる。伸び縮みを主に表す対角項にも角度の変化速度![]() が
あるので,物理的には少しわかり難い結果になっているが,実は
この場合も,式(12.40)の主ストレッチと
式(12.41)の主方向を考慮すれば,
前例と同様
が
あるので,物理的には少しわかり難い結果になっているが,実は
この場合も,式(12.40)の主ストレッチと
式(12.41)の主方向を考慮すれば,
前例と同様
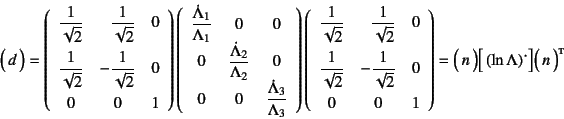
という関係を得ることができる。 やはり変形速度は対数ひずみ速度に相当している。
以上の2例では,
材料が感じる変形の主方向に変化が無い(
![]() )特殊な例であった。
そこで,最後にもう少し一般化して
)特殊な例であった。
そこで,最後にもう少し一般化して
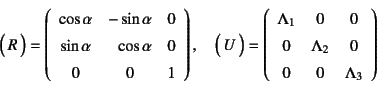
という変形を考えてみよう。
これは,材料にとっての変形の主方向が時々刻々変化(![]() )しながら,
伸び縮み(
)しながら,
伸び縮み(![]() )と剛体的な回転(
)と剛体的な回転(![]() )を伴う一般的な運動である。
簡単のために,これ以下では
)を伴う一般的な運動である。
簡単のために,これ以下では![]() 軸に関するものをすべて省略する。
前節までの各関係式や定義に代入していくと,以下のような結果が得られる。
軸に関するものをすべて省略する。
前節までの各関係式や定義に代入していくと,以下のような結果が得られる。
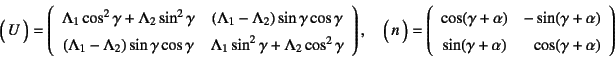
であり,スピンはそれぞれ
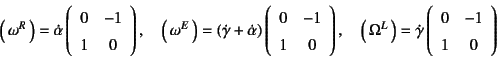
となる。材料が感じる歪みの向きが変化する回転成分が
![]() であり,
歪みとは関係なく剛体的に回転する成分が
であり,
歪みとは関係なく剛体的に回転する成分が
![]() になっている。
これを用いて
になっている。
これを用いて
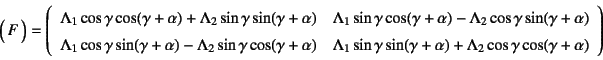
を得る。この時間微分等を用いれば
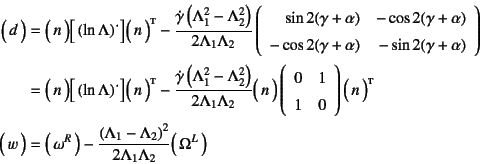
と求められる。いずれも第2項が![]() ,つまり材料にとっての
力の主方向の変化率に関連した項である。
これは,大きなせん断変形
,つまり材料にとっての
力の主方向の変化率に関連した項である。
これは,大きなせん断変形
![]() が
存在する場での,それぞれせん断変形の変化率とスピン成分である。
特に変形速度の第2項は跡が零になっているので体積変化を伴わない成分である。
また非対角項しか存在せず,
が
存在する場での,それぞれせん断変形の変化率とスピン成分である。
特に変形速度の第2項は跡が零になっているので体積変化を伴わない成分である。
また非対角項しか存在せず,
![]() の
せん断変形に変化率
の
せん断変形に変化率![]() が乗算されていることから,
せん断変形速度成分になっていることもわかる。
ただし,スピンの第2項は比較的変形が小さい段階,
つまり
が乗算されていることから,
せん断変形速度成分になっていることもわかる。
ただし,スピンの第2項は比較的変形が小さい段階,
つまり
![]() ,
,
![]() の近似をすると
の近似をすると
のように,第1項に比べて無視できる2次項になる。
したがって,スピンの場合は第1項が物理的には主要な意味を
与えてくれると考えていいだろう。
結局,極分解したときの回転![]() の変化率
の変化率
![]() が
主なスピンであると考えられる。
が
主なスピンであると考えられる。
少しわかり難くはなるが,式の展開によって厳密に物理的な意味を模索してみよう。
スペクトル表示を用いると便利なので行列計算を行う。
式(12.17)の変形勾配を時間微分すると
となる。これを式(12.51)に代入して式(12.17)を
用いて整理すると
を得る。一方,式(12.22a)の![]() のスペクトル表示を用いて
整理すると
のスペクトル表示を用いて
整理すると
![\begin{eqnarray*}
\matrx{\dot{U}}\matrx{U}^{-1}&=&
\left(
\matrx{\Omega^L}\matrx...
...a} \right]
\matrx*{N}+
\matrx{U}\matrx*{\Omega^L}\matrx{U}^{-1}
\end{eqnarray*}](s5img331.gif)
となる。この結果を上式(![]() )に代入して
式(12.17) (12.31)を考慮すると
)に代入して
式(12.17) (12.31)を考慮すると
と表現できることがわかる。 速度勾配の表現のままでは,特に最後の項はまだ少しわかり難い。
最終的に,これを式(12.52)に代入すれば,
変形速度は
と分解して表すことができる。この第1項の![]() は
は
あるいは式(12.25)を用いてEuler的表現にして
式(12.55)を用いると
のように対称テンソルとして定義されるが,これが,前節の最後の例で現れた
主軸の回転に伴って大きなせん断ひずみが生み出すせん断変形速度である。
当然であるが,極分解して求めた回転![]() の速度
の速度![]() は
剛体回転的な意味を持っていることから,変形速度には含まれていない。
は
剛体回転的な意味を持っていることから,変形速度には含まれていない。
ところで,この式(12.64)の跡を
求めると,式(12.58)の体積変化の表現から
であることから,第2項の跡は零
になる。
つまり,第1項の対数ひずみ速度![]() は非回転変形速度成分
(体積変化速度)であり,
第2項
は非回転変形速度成分
(体積変化速度)であり,
第2項![]() は等体積変形速度成分
(せん断変形速度)になっていて,物理的にはとてもわかり易い。
ただ注意して欲しいのは,対数ひずみ速度は対数ひずみ
は等体積変形速度成分
(せん断変形速度)になっていて,物理的にはとてもわかり易い。
ただ注意して欲しいのは,対数ひずみ速度は対数ひずみ![]() の
変化率ではないことだ。つまり,式(12.46)の変化率を求めたとき
の
変化率ではないことだ。つまり,式(12.46)の変化率を求めたとき
になっていることに注意する。
一方スピンは,式(12.56)に式(![]() )を代入すれば
)を代入すれば
と求められる。
前節の最後の例でもわかるように,中括弧でくくった第2項が
主軸のスピン
![]() に伴って
大きなせん断ひずみが生み出すスピンに相当する。
ちなみに,スピンの右辺の最初の2項は
式(12.55)の関係を用いればまとめることができ
に伴って
大きなせん断ひずみが生み出すスピンに相当する。
ちなみに,スピンの右辺の最初の2項は
式(12.55)の関係を用いればまとめることができ
あるいは,式(12.67)の誘導と同様
のような反対称テンソルとして表されるが,
前節の例からもわかるように,
比較的変形が小さい場合の主要項は
![]() になるので,
式(12.69)の表現に留めておいた(
になるので,
式(12.69)の表現に留めておいた(
![]() は
用いない)方がいいだろう。
は
用いない)方がいいだろう。
さて,ここまでは純粋に幾何学的・数理物理的に物体の運動を表現する方法と 結果を示したに過ぎない。 ただ変形できる物体の力学への応用という観点から, 例えば実測できる量なのか否かといった物理的な意味についても説明してきた。 もし読者が初学者で,以上の式の展開を自らの手を動かして実行していないとすると, これ以下へと読み進んだとしても,それほど理解はできないことが予想される。 特に,手を動かさずにぼんやりと式を眺めて何となくわかったような気がしている 読者は,これ以下を読むと怪我をする可能性がある。 ここで立ち止まって,先を読むか,ここまでの勉強をやり直すか, 有限変形の勉強を諦めるか,という決断をした方がいい。
さて異なるメカニズムの変形が,例えば塑性変形が生じたあと
弾性変形が生じるような2段階の変形が
初期配置から追跡できたとして,よく
という記述がなされる。 ここに,上添え字の`e'は弾性変形による成分を,`p'は塑性変形の 成分を示している。 全体の変形勾配は,塑性変形が発生したあとに その非適合変形を補うために弾性変形が発生すると考えているのである。 これはよく乗算則(乗算分解)12.10と 呼ばれているが,しかし,これは単なる偏微分の連鎖律に過ぎない。 物理的に例えば流れ則は積分できないこと等を考えると
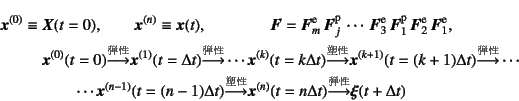
のように位置が時々刻々更新したと考える方が一般的で素直だろう。
したがって変形勾配は,連鎖律により
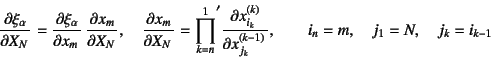
のように,時々刻々の乗算則になる。![]() に
プライムを付けたのは,
に
プライムを付けたのは,![]() を
を![]() から1ずつ減ずることを意味している。
このような順番で変形が起きたとすれば
から1ずつ減ずることを意味している。
このような順番で変形が起きたとすれば
のように考えればいい。これから,最終的な変形勾配は単純な連鎖律から
と乗算で表現できる。この変化率を,最終的な現配置![]() でとると
でとると
となる12.11ので,
これを用いて最終的な
速度勾配
![]() を算定すると
を算定すると
という関係を得る。
現配置での瞬間的な変形率を考えているので,添え字には大文字が現れていない
ことに注意する。
第2項の![]() は配置
は配置![]() で
定義されているのに対し,この速度勾配は現配置の
で
定義されているのに対し,この速度勾配は現配置の![]() で
定義されているため,
第2項にはその補正
で
定義されているため,
第2項にはその補正
![]() と
と
![]() がなされている。
塑性論の特性から小さい変形履歴ステップ
がなされている。
塑性論の特性から小さい変形履歴ステップ![]() をとらざるを得ないことから,
そのステップが弾性変形であろうと塑性変形であろうと,
この補正の
をとらざるを得ないことから,
そのステップが弾性変形であろうと塑性変形であろうと,
この補正の
![]() と
と
![]() は
ほとんどKroneckerのデルタになり,
は
ほとんどKroneckerのデルタになり,
![]() ,
,
![]() と考えてよく,
したがって近似的に加算則(加算分解)の
と考えてよく,
したがって近似的に加算則(加算分解)の
ができると考え[93]てもいい。
あるいは上式の第2項を第1項と同じ配置![]() で
で
と定義し直した上で,加算則が厳密に成立する[58]と考えればいい。
そしてこの式を根拠に,弾塑性理論では変形速度もスピンも
弾性成分と塑性成分の加算で
が成立するとしている。
実際,材料試験の様子を考えてみると,
[弾性|塑性]変形だけを測定したあと,[塑性|弾性]変形成分を
測定しているわけではない。
ある荷重増分に対して,![]() がどのように変化するのか測定しつつ,
右辺のどちらかの量を例えば除荷のような手段で弾性成分を測定するといった,同じ配置からの観察で同時に測定をしている。
つまり,上の式で測定しているの
は,
がどのように変化するのか測定しつつ,
右辺のどちらかの量を例えば除荷のような手段で弾性成分を測定するといった,同じ配置からの観察で同時に測定をしている。
つまり,上の式で測定しているの
は,
![]() と
と
![]() であると
考えればいい。
そのため,加算のモデルも厳密に成立すると理解しても構わない。
例えば図-12.6のように,転位が試験片の表面に
出た瞬間,中央の図に示したように引張り試験の載荷軸に
ずれ(非適合)が生じようとする。
そのとき前節最後の例の記号と使うと,この塑性的なずれを,
さらなる塑性的な回転と弾性的な回転を合わせた
であると
考えればいい。
そのため,加算のモデルも厳密に成立すると理解しても構わない。
例えば図-12.6のように,転位が試験片の表面に
出た瞬間,中央の図に示したように引張り試験の載荷軸に
ずれ(非適合)が生じようとする。
そのとき前節最後の例の記号と使うと,この塑性的なずれを,
さらなる塑性的な回転と弾性的な回転を合わせた![]() で回転させ,
また材料中の主軸も
で回転させ,
また材料中の主軸も![]() で回転させると同時にそれに見合う弾塑性的な
せん断変形も生じさせた上で,載荷軸のずれを解消して一番右の
状態(適合な変形状態)に落ち着く。そしてこの二つのメカニズムが,
転位が表面および結晶粒子界面に達する度に時々刻々生じている。
そして通常,この弾性的な変形と
塑性的な変形,
で回転させると同時にそれに見合う弾塑性的な
せん断変形も生じさせた上で,載荷軸のずれを解消して一番右の
状態(適合な変形状態)に落ち着く。そしてこの二つのメカニズムが,
転位が表面および結晶粒子界面に達する度に時々刻々生じている。
そして通常,この弾性的な変形と
塑性的な変形,
![]() と
と
![]() は
同時に起き,測定される。
ただもちろん節-9.2.3や節-9.3.3で
示したように流れ則は積分不可能であることから,有限変形の場合は
どのようなひずみ尺度
は
同時に起き,測定される。
ただもちろん節-9.2.3や節-9.3.3で
示したように流れ則は積分不可能であることから,有限変形の場合は
どのようなひずみ尺度
![]() を用いたとしても
を用いたとしても
であることには十分注意する必要がある。