



Next: J.3 共変微分
Up: J. テンソル演算について
Previous: J.1 座標と基底ベクトル
最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
同じ基底同士の内積を計量テンソル
と呼び
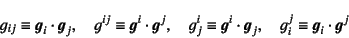 |
(J.13) |
等と定義される。これを用いれば,共変成分と反変成分を
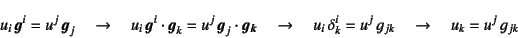 |
(J.14) |
等のように関係付けること(添え字の入れ替え)ができる。
また,
交代記号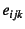 (テンソルではない)を
(テンソルではない)を
 |
(J.15) |
と定義すると,例えば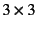 の行列
の行列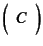
の行列式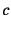 は
は
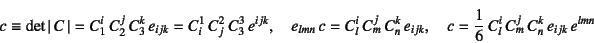 |
(J.16) |
と書くことができる。
また二つのベクトル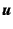 ,
, 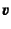 の外積
の外積
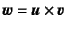 は
は
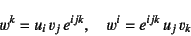 |
(J.17) |
と成分表示できる。
一方,計量テンソルの行列式を
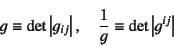 |
(J.18) |
と定義しておくと,
置換テンソル
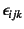 は
は
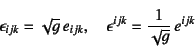 |
(J.19) |
と定義される。
これとKroneckerのデルタの間には
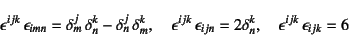 |
(J.20) |
の関係が成り立つ。
最新版を正確に読むためには pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。




Next: J.3 共変微分
Up: J. テンソル演算について
Previous: J.1 座標と基底ベクトル
Iwakuma Tetsuo
Mon, 18 Feb 2013 12:50:55 +0900
: Stardate [-28]8120.80
![]() の行列
の行列![]()
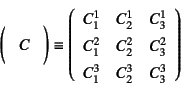
![]() は
は
![]() ,
, ![]() の外積
の外積
![]() は
は