最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。

J.1 座標と基底ベクトル

図 J.1: 斜交座標

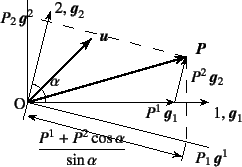
文献[24]とそれを用いた西野教授の「応用弾性学」の 講義で習ったことのうち，なんとなくの印象を得ることができる部分を 列挙してみた。本当は， 斜橋等の設計では斜交座標系で，曲線橋等の設計では直角座標ではない座標系で 力学を論ずる必要がある。図-J.1のような 斜交座標を考え， 下添え字のベクトル$\fat{g}_i$ ($i=1$, 2)はその方向の単位の基底ベクトルとする。 図のように，下添え字の単位長さの 基底ベクトル$\fat{g}_j$の成分を上添え字を付けて定義し， それを反変成分 と呼び，任意のベクトルを

$$\fat{P}=P^1 \fat{g}_1+P^2 \fat{g}_2$$ (J.1)

のように成分表示（分解）できると考える。 さて図には描いていないが，水平($x$)方向の単位基底ベクトルを$\fat{i}_1$とし， 鉛直($y$)方向の単位基底ベクトルを$\fat{i}_2$とすると， ベクトル$\fat{P}$の水平($x$)方向および鉛直($y$)方向成分$P_x$, $P_y$は それぞれ

$$P_x=P^1+P^2 \cos\alpha, \quad P_y=P^2 \sin\alpha$$

になるので，$\fat{P}$が力で$\fat{u}$が変位だった場合には， 仕事$W$は二つのベクトルの内積で定義され

$$W=\fat{u} \fat{P}=\left(u^1+u^2 \cos\alpha\right) \left(P^1+P^2 \cos\alpha\right) +u^2 \sin\alpha P^2 \sin\alpha$$

となることから

$$W=\fat{u} \fat{P}=\left(u^1+u^2 \cos\alpha\right) P^1+ \left(u^2+u^1 \cos\alpha\right) P^2$$ (J.2)

と書くことができる。

一方，上式(J.2)を眺めながら

$$u_1\equiv u^1+u^2 \cos\alpha, \quad u_2\equiv u^2+u^1 \cos\alpha$$ (J.3)

と定義すると，仕事は

$$W=\sum_{i=1}^3 u^i P_i$$ (J.4)

と書くことができている。実は，式(J.3)の下添え字を 付した成分は，図の上添え字の基底ベクトル$\fat{g}^i$ ($i=1$, 2)の成分で， 式(J.1)に対応して，任意のベクトルが

$$\fat{u}=u_1 \fat{g}^1+u_2 \fat{g}^2$$ (J.5)

のようにも成分表示（分解）できるのである。 この下添え字の成分を共変成分 と呼ぶ。

さて，上式(J.2)の仕事は

$$W=u^1 \left(P^1+P^2 \cos\alpha\right)+ u^2\left(P^2+P^1 \cos\alpha\right)$$ (J.6)

とも書くことができる。ここで

$$P_1=P^1+P^2 \cos\alpha, \quad P_2=P^2+P^1 \cos\alpha$$ (J.7)

と書くことにすると，これは式(J.3)との比較からも 明らかなように，$\fat{P}$の共変成分である。 つまり

$$\fat{P}=P_1 \fat{g}^1+P_2 \fat{g}^2$$ (J.8)

となる。さて図からも明らかなように，$\fat{g}^i$は 単位長さではなく $\dfrac{1}{\sin\alpha}$の 長さを持っており，2種類の異なる基底ベクトル同士は直交し

$$\left\vert\fat{g}^i\right\vert=\dfrac{1}{\sin\alpha}, \quad \fat{g}^m \fat{g}_n=\delta^m_n$$ (J.9)

の関係が成立する。ここに$\delta^m_n$はKroneckerのデルタである。 結局仕事は

$$W=\sum_{i=1}^3 u_i\fat{g}^i P^j\fat{g}_j= \sum_{i=1}^3 u_iP... ... \sum_{i=1}^3 u_i P^i=\sum_{i=1}^3 u^i P_i=u_i P^i=u^i P_i$$ (J.10)

と書くことができる。ただし，右二つの式にあるように 通常は$\sum$の記号を省略し，同じ添え字が上下に2回出てくる場合にのみ， それは1から3まで総和をとる（総和規約 ）ものとする。

さて$\fat{g}_i$方向の座標を$\xi^i$と記すことにすると， 水平・鉛直の直角座標の$x^i$との間には

$$x^1=\xi^1+\xi^2 \cos\alpha, \quad x^2=\xi^2 \sin\alpha,$$ (J.11)

の関係がある。実は基底ベクトルは

$$\fat{g}_i=\D{x^j}{\xi^i} \fat{i}_j$$ (J.12)

とも定義される。具体的に式(J.11)を代入すると

$$\fat{g}_1=\fat{i}_1, \quad \fat{g}_2=\cos\alpha \fat{i}_1+\sin\alpha \fat{i}_2$$

のように，幾何学的に求められるものと一致する。 これはどちらも無次元の単位ベクトルであるが， 式(J.9)のように$\fat{g}^i$は単位ベクトルではないことには 注意する。

最新版を正確に読むためには pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。