最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。

J.3 共変微分

さて，極座標におけるナブラやラプラシアンは結構面倒な 形をしていた。それは何故だろう。 例えば任意のベクトル$\fat{u}$を $\fat{u}=u^i \fat{g}_i$と 成分表示したとしよう。このベクトルの変化つまり微係数は， 成分のみならず基底ベクトルも微分する必要があることに気付く。 極座標等では直角座標とは異なり，基底ベクトルが一定ではないことが 微係数の表現を面倒にしているのである。 例えば$\fat{g}_j$方向の座標$\xi^j$でこれを微分すると

$$\D{\fat{u}}{\xi^j}= \D{\left(u^i \fat{g}_i\right)}{\xi^j}= \D{u^i}{\xi^j} \fat{g}_i+ u^i\D{\fat{g}_i}{\xi^j}$$

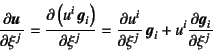
という計算をしなければならない。基底ベクトルは 式(J.12)のように表現できたことを思い起こすと

$$\D{\fat{g}_i}{\xi^j}=\fat{g}_{i,j}= \D[2][1][\xi^j]{x^k}{\xi^i} \fat{i}_k$$

を求めておく必要がある。ここに，添え字中のコンマは次の 添え字の座標で偏微分することを意味する。 そこで

$$\fat{g}_{i,j}=\Gamma_{ijk} \fat{g}^k=\Gamma_{ij}^k \fat{g}_k$$ (J.21)

と表すことにする。この$\Gamma_{ijk}$等はChristoffelの記号 と呼ばれている。 式(J.21)を用いれば，上述のベクトルの微係数は

$$\D{\fat{u}}{\xi^j}= \D{\left(u^i \fat{g}_i\right)}{\xi^j}= ... ...a^i_{jk}\right) \fat{g}_i =\left.u^i\right\vert _j \fat{g}_i$$ (J.22)

と表すことができる。ここに $\left.u^i\right\vert _j$は共変微係数 と呼ばれる。

最新版を正確に読むためには pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。