- 9.3.3.1 一般的な表現
- 9.3.3.2 継続された載荷の場合
- 9.3.3.3 純せん断の場合
- 9.3.3.4 べき乗則硬化の場合
- 9.3.3.5 複雑な経路に沿った数値解
- 9.3.3.6 整合条件を用いない数値解析--降伏条件を高次項まで満足させる場合
- 9.3.3.7 べき乗則硬化の場合の数値解
最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
前節ではMisesの降伏条件とPrandtl-Reussの流れ則を前提とした 弾塑性構成方程式の考え方について説明した。 ここではその考え方をもう少し一般化して, 降伏関数を限定せず, いわゆる一般化されたPrandtl-Reussの構成方程式 を誘導しよう。さらに降伏条件と流れ則を分離するような,さらなる 一般化についての考え方も説明する。
まず,
降伏の主な要因がせん断変形であることから,
その降伏条件は偏差応力の不変量で与えるのが自然である。
つまり![]() と考えるのが素直であろう。
ここに
と考えるのが素直であろう。
ここに![]() は式(9.22b)で定義した偏差応力の第3不変量である。
この降伏関数を用いた降伏条件
は式(9.22b)で定義した偏差応力の第3不変量である。
この降伏関数を用いた降伏条件![]() は,
応力の6次元空間の曲面とも解釈でき,その曲面を降伏曲面
と呼ぶ。
は,
応力の6次元空間の曲面とも解釈でき,その曲面を降伏曲面
と呼ぶ。
前節で用いたMisesの降伏条件
は,偏差応力の第2不変量のみを用いて
と定義したことになる。![]() は応力成分で表すと
は応力成分で表すと
となるので,主応力で書き直すと,この条件は
とも書くことができる。
この条件は,図-9.18のような主応力軸を
直交する3軸とする座標系で,
![]() の直線(静水圧軸あるいは等方応力軸)方向の
単位ベクトル
の直線(静水圧軸あるいは等方応力軸)方向の
単位ベクトル![]() を法線とする平面(
を法線とする平面(![]() 平面
と呼ぶ)内に円断面を持つ,無限に長い円柱形になる。
それは,等方応力では降伏しない9.26からである。
平面
と呼ぶ)内に円断面を持つ,無限に長い円柱形になる。
それは,等方応力では降伏しない9.26からである。
これに対し,物体内の最大せん断応力がある規定値に達したときに
降伏するという規準もあり得る。特に金属の単結晶のように,
結晶方位で決定されるすべり面上のすべりで塑性変形が生じる場合は,
この最大せん断応力による規準の方が適していると考えられる。
任意の応力状態における最大せん断応力
は,節-3.5.2 (3)で
示したMohrの円を見れば明らかなように,主応力の差の半分である。
つまり,二つずつの主応力差の
半分,
![]() ,
(
,
(
![]() )のうちの最大値(最大せん断応力)で
降伏を規定すればいい。この条件はTrescaの降伏条件
と呼ばれ,例えば
)のうちの最大値(最大せん断応力)で
降伏を規定すればいい。この条件はTrescaの降伏条件
と呼ばれ,例えば
と表すことができる。このままでは偏差応力との関係が明確ではないが,
偏差応力の不変量と主応力の関係を用いて書き直すと
がTrescaの降伏条件になる。
ただし,一見滑らかな関数に置き換えてしまっているため,
例えば
![]() のみが非零であるような1軸状態に
この式(9.53)を用いると負になってしまう等,
使用には注意が必要である。そのため
のみが非零であるような1軸状態に
この式(9.53)を用いると負になってしまう等,
使用には注意が必要である。そのため![]() ではなく
ではなく![]() と記した。
そういう観点からは,あるいは
と記した。
そういう観点からは,あるいは
| (9.54) |
と定義した方が正しいかもしれないが,使い難いことには変わりがない。
これに対し,主偏差応力![]() (X=I, II, III)が
主応力差と
(X=I, II, III)が
主応力差と
という関係にあることと,式(9.23)の
主偏差応力![]() の表現とを比べることによって,上のTrescaの条件は
の表現とを比べることによって,上のTrescaの条件は
と表すこと[57]もできる。ここに
![]() はLode角
と呼ばれるもので
はLode角
と呼ばれるもので
で定義されている。式(9.24)の
角度![]() との関係も示しておいた。
との関係も示しておいた。
ところでここでは,この代表的な二つの降伏関数同士で,
降伏せん断応力![]() が共通になるように定義した。
つまり図-9.19の左図のA, B点(
が共通になるように定義した。
つまり図-9.19の左図のA, B点(
![]() ,
,
![]() の
純せん断状態)が両条件で一致している。
したがって,Trescaの降伏条件に基づけば,1軸状態の
降伏引張り応力
の
純せん断状態)が両条件で一致している。
したがって,Trescaの降伏条件に基づけば,1軸状態の
降伏引張り応力
![]() は
は
という関係にあり,Misesの降伏条件に基づいた式(9.27)の 関係とは異なっていることに注意する。 この図-9.19の左図は, よく教科書等に描かれているものとは異なり,Trescaの 条件の方がMisesのそれの外側に位置しているが,これは,上述のように, お互いの降伏せん断応力を一致させたからである。 もし両条件の降伏引張り応力を一致させると,右図のような,よく見る 図になる。この場合の降伏せん断応力と降伏引張りの関係は, 式(9.27)のMisesのそれと同じになる。 金属材料の実験値はこの右図のMisesとTrescaの条件の間の ややMises側に分布する[92]ため,Misesの降伏条件が よく用いられている。
さてDruckerは,次の条件を満足する材料を「安定な材料」と定義した。
これをDruckerの公準
と呼ぶ。ここに積分は,塑性変形を伴いながら変形する経路に沿った
履歴の累積を表しており,
![]() はそのような
履歴の開始時の任意の応力状態である。
この条件式(9.58)が降伏状態近傍の非常に微小な
任意の時間の間に成立しなければならない条件を
はそのような
履歴の開始時の任意の応力状態である。
この条件式(9.58)が降伏状態近傍の非常に微小な
任意の時間の間に成立しなければならない条件を
と記すことができそうだ。 任意の塑性変形は,この条件式(9.59)を満足するように 生じるものとすることが基本となっている。
図-9.20には
直感的かつ短絡的な説明を描いておいたが,履歴Bのような軟化材料や,
履歴Cのような材料を除外しているものと考えればいい。
この公準は,解の唯一性とも密接に関係している。
上式の![]() や
や
![]() ・
・
![]() の
定義を明確にした上で,上の安定規準が最大塑性仕事の原理
に相当することも示されているが,
詳細については文献[34]等を参照のこと。
ただし実験等と比較すると,
この基準を満足する材料は安定過ぎる挙動を示すことが多いので,
この条件を緩和したモデルも多く存在する。
の
定義を明確にした上で,上の安定規準が最大塑性仕事の原理
に相当することも示されているが,
詳細については文献[34]等を参照のこと。
ただし実験等と比較すると,
この基準を満足する材料は安定過ぎる挙動を示すことが多いので,
この条件を緩和したモデルも多く存在する。
Hill[34]の概説に沿って,等方材料の降伏条件を一般化しておく。
それによれば,降伏条件式(9.25)は
と表される。ここでも初期降伏後の履歴依存を明示するために,
せん断降伏応力![]() を累積塑性ひずみ
を累積塑性ひずみ
![]() の
関数として定義した。
また基本的な扱いに留めるために,まだ
の
関数として定義した。
また基本的な扱いに留めるために,まだ![]() はそれほど一般化されていない。
さて,弾性状態でも降伏した状態でもいいが,
ある任意の応力状態
はそれほど一般化されていない。
さて,弾性状態でも降伏した状態でもいいが,
ある任意の応力状態
![]() から出発して塑性変形が生じるような
変形履歴をたどり,降伏条件式(9.60)を満足する
応力状態
から出発して塑性変形が生じるような
変形履歴をたどり,降伏条件式(9.60)を満足する
応力状態![]() に達したとしたとき,
任意の応力増分
に達したとしたとき,
任意の応力増分
![]() に対して
生じる塑性ひずみ増分
に対して
生じる塑性ひずみ増分
![]() は
は
を満足しなければならない。
実は,この条件がどちらも同時に満足されるためには
必要がある。というのも
からである。制約1は,
この節で紹介したMisesの降伏関数もTrescaの降伏関数も満足している。
また制約2は,流れ則
が
で与えられる9.27ことを意味する。というのも,
![]() は
その曲面
は
その曲面
![]() の外向き法線「ベクトル」9.28に相当するからである。
ただし,前節の
の外向き法線「ベクトル」9.28に相当するからである。
ただし,前節の
![]() が応力の逆数の次元を持つのに対し,
ここの
が応力の逆数の次元を持つのに対し,
ここの![]() は,式(9.60)のような
は,式(9.60)のような![]() の
定義と式(9.61)の流れ則のもとでは無次元量になることには注意する。
この条件を法線則
と呼んでいる。応力空間と塑性ひずみ増分空間を同じ「座標系」に
重ねることは非常に考え難いとは思われるが,
式(9.30)が発見されるに至った実験観察から,
「応力」と「塑性ひずみ増分」は共軸性
を有していると考えているので,重ねて考えられるのである。
の
定義と式(9.61)の流れ則のもとでは無次元量になることには注意する。
この条件を法線則
と呼んでいる。応力空間と塑性ひずみ増分空間を同じ「座標系」に
重ねることは非常に考え難いとは思われるが,
式(9.30)が発見されるに至った実験観察から,
「応力」と「塑性ひずみ増分」は共軸性
を有していると考えているので,重ねて考えられるのである。
塑性ひずみ増分が生じる変形状態では降伏条件式(9.60)が成立し
続けなければならないので,整合条件を満足し
が成立する。第2項に流れ則の式(9.61)を代入すると
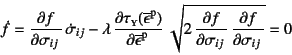
となることから,最終的に
(9.62)
となる。![]() は硬化係数
である。これを再度流れ則の式(9.61)に戻せば
は硬化係数
である。これを再度流れ則の式(9.61)に戻せば
を得る。これが一般化されたPrandtl-Reussの関係 である。 再度Misesの降伏関数を用いた場合には式(9.36)の 関係が成立するので,この式(9.63)は前節の 式(9.38)に一致する。 弾性成分との和および逆関係の誘導は,次節に示す結果の特別な場合に 相当するので割愛する。
また式(9.62a)から,載荷や除荷も同様に降伏曲面の法線を用いて
規定できることがわかる。すなわち
となる。つまり,降伏曲面の法線「ベクトル」と 応力増分「ベクトル」の内積で各状態が規定しようとするのである。 内積が正であるということは,降伏曲面が凸である限り, 応力増分がこの降伏曲面から 外に出ようとしていると解釈することができる。 逆に内積が負であれば,応力増分は 降伏曲面の内側に戻ろうとしていることに相当しており,これが 上式では除荷として規定されていることになる。Misesの降伏関数を 用いた場合には式(9.36)の 関係が成立するので,この式(9.64)は前節の 式(9.39)に一致する。
さらなる一般化が塑性ポテンシャルの導入によって可能になる。
すなわち,前節の流れ則の式(9.61)から明らかなように,
降伏条件と流れ則の間には密接な関係があったが,
ここではそれを緩和しようとするものである。
ここもHill[34]の記述をそのまま引用して列挙する。
式(9.60)から,
例えば単調に載荷し続けて塑性変形を発生させ続けた場合には,
上式(9.60)の![]() も
も![]() も単調に
増加し続けるものの,
も単調に
増加し続けるものの,![]() は零を満足し続ける。
したがって「載荷」
という状況は
は零を満足し続ける。
したがって「載荷」
という状況は
という条件で定義できそうである。
これに対し,一旦材料が降伏したあと,降伏条件は満足し続けるものの,
塑性変形は新たには生じないまま,単に応力状態のみが変化する「中立載荷」
の場合には上式(9.60)の
右辺の![]() も不変であるし,同時に
も不変であるし,同時に![]() も不変である。つまり
も不変である。つまり
という条件で定義できる。さらに,一旦降伏した材料の外力が取り除かれ,
材料が弾性に戻る「除荷」
の場合には,![]() は不変なまま降伏条件を満足しなくなるので
は不変なまま降伏条件を満足しなくなるので
で定義できそうだ。
したがって,「載荷」と「中立載荷」の上式での比較から,塑性ひずみ増分は
という関係を満足すると考えてよさそうである。ただし,テンソル![]() は
は
を満足するものとする。
一つ目の条件は塑性的な体積変形は生じないというものであり,
二つ目は前節で説明した流れ則が持つべき制約条件である。
ただこのように考えると,このテンソル![]() は
降伏関数
は
降伏関数![]() と必ずしも直接の関係が無くてもいいということになる。
そこで,この条件を満足する一つの形として
と必ずしも直接の関係が無くてもいいということになる。
そこで,この条件を満足する一つの形として
を仮定することができる。ここに![]() はある種の硬化係数
であり,
はある種の硬化係数
であり,![]() を塑性ポテンシャル
と呼ぶ。
式(9.70)を式(9.68)に
代入すれば,塑性ひずみ増分は
を塑性ポテンシャル
と呼ぶ。
式(9.70)を式(9.68)に
代入すれば,塑性ひずみ増分は
と表されることになる。
載荷され続ける状態では,上記のように降伏条件![]() は満足され続けるので,
式(9.60)の増分は零となり
は満足され続けるので,
式(9.60)の増分は零となり
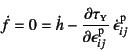
を常に満足していることになる。この条件は整合条件
である。
この式の右辺第2項に式(9.71)を
代入すれば,載荷時には![]() が非零の正であることから,
硬化係数が
が非零の正であることから,
硬化係数が
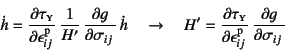
と表現される。
つまり,変形履歴においてせん断降伏応力![]() が
どのように変化するか(硬化則)
という材料特性を実験等で求めておけば,
硬化係数
が
どのように変化するか(硬化則)
という材料特性を実験等で求めておけば,
硬化係数![]() を具体的に表現することができる。
さて通常,式(9.71)を式(9.30)に
対応させて表現したものが用いられているが,
それは
を具体的に表現することができる。
さて通常,式(9.71)を式(9.30)に
対応させて表現したものが用いられているが,
それは
![]() を
を![]() と置き
と置き
としたもので,これを一般的な流れ則
と呼んでいいだろう。
この法則は式(9.61)とほぼ同じであるが,
塑性ポテンシャルを導入することによって,![]() が
必ずしも降伏関数
が
必ずしも降伏関数![]() と同じである必要は無いようになっている。
と同じである必要は無いようになっている。
簡単のために降伏関数が
で定義されるものとする。ここに
![]() は
式(9.26)で定義した累積塑性ひずみである。
また,塑性ポテンシャルは別の関数
は
式(9.26)で定義した累積塑性ひずみである。
また,塑性ポテンシャルは別の関数![]() で定義されるものとしよう。
流れ則は式(9.72)で与えられる。
まず状態を規定するために,前節でのHillの考察を用いる。
載荷は式(9.65)の場合である。つまり
で定義されるものとしよう。
流れ則は式(9.72)で与えられる。
まず状態を規定するために,前節でのHillの考察を用いる。
載荷は式(9.65)の場合である。つまり
がその状態を規定している。同様に,中立載荷と除荷も 式(9.66) (9.67)のように 考えればよく,各状態は
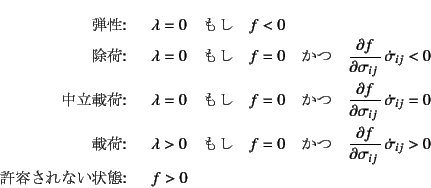
と規定できる。これは前節の式(9.64)と同じである。
次に整合条件は,式(9.73)から
となるので,流れ則の式(9.72)を第2項に
代入すれば,
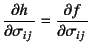 なので
なので
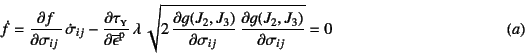
と定義しておけば
となる。この結果を,再度,流れ則の式(9.72)に戻せば
を得る。塑性ポテンシャル![]() の導入によって,
硬化係数
の導入によって,
硬化係数![]() の定義と塑性ひずみ増分の向きが一般化された。
の定義と塑性ひずみ増分の向きが一般化された。
さて,弾性成分は
式(3.54)の弾性コンプライアンスを用いて
という関係を満たすものとすると,この式と式(9.75)を
加算則の式(9.21)に代入すれば
という関係を得る。したがって,弾塑性接線コンプライアンス
を
と表すことができる。
ここに![]() は式(9.49)で定義したスィッチである。
は式(9.49)で定義したスィッチである。
物理的に![]() を考察するには,以上のような定式化が必要であるが,
誘導された増分ひずみ・増分応力関係の逆関係である
応力増分とひずみ増分の関係を得ることは一般には困難が伴う。
そこでSimoとHughes[67]の汎用的な誘導法をここに示しておこう。
式(
を考察するには,以上のような定式化が必要であるが,
誘導された増分ひずみ・増分応力関係の逆関係である
応力増分とひずみ増分の関係を得ることは一般には困難が伴う。
そこでSimoとHughes[67]の汎用的な誘導法をここに示しておこう。
式(![]() )に式(9.74)を代入すると
)に式(9.74)を代入すると
となる。一方弾性関係は,式(3.52)と,
ひずみの弾性・塑性の加算分解式(9.21)を考慮すれば
となり,これに流れ則を代入すれば
と書くことができる。式(![]() )を式(
)を式(![]() )に
代入すると
)に
代入すると
となるので,これから![]() を求めると
を求めると
となる。式(![]() )に比べると,物理的にはわかり難い形をしている。
これを再度,式(
)に比べると,物理的にはわかり難い形をしている。
これを再度,式(![]() )に代入し戻せば
)に代入し戻せば
となるので,結局
| (9.80) |
と定義することができる。
ここに![]() は式(9.49)で定義したスィッチである。
は式(9.49)で定義したスィッチである。
一般化されたPrandtl-Reussの式(9.63)は,
式(9.75)において
と置いたこと(元々のPrandtl-Reussの式(9.38)は上式の
括弧内のように置いたこと)に相当する。![]() と
と![]() の間に
この式(9.81)(括弧内を除く)が成立する
流れ則を,関連流れ則
と呼び,したがってそうではないものを非関連流れ則
と呼んでいる。Prandtl-Reussの式(9.38)の場合は,
降伏関数と塑性ポテンシャルに
の間に
この式(9.81)(括弧内を除く)が成立する
流れ則を,関連流れ則
と呼び,したがってそうではないものを非関連流れ則
と呼んでいる。Prandtl-Reussの式(9.38)の場合は,
降伏関数と塑性ポテンシャルに![]() のみを用いた理論で
あることから,
のみを用いた理論で
あることから,![]() 流れ理論
とも呼ばれている。また,この場合は
流れ理論
とも呼ばれている。また,この場合は
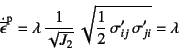 |
(9.82) |
となるので,![]() の物理的な意味は
累積塑性ひずみ増分そのものであることもわかる。
の物理的な意味は
累積塑性ひずみ増分そのものであることもわかる。
ところで,材料非線形性に関係した安定問題を扱うモデルで,塑性軟化 の設定をする研究があるように思われるが, その場合には例えば「載荷」と「除荷」をどう定義すべきだろうか。 例えば式(9.47)の 弾塑性接線係数に1軸応力状態の 設定をして行列表示した場合, 接線係数が正定値である条件からは,正の硬化係数しかあり得ない。
しかし,
軟化するということは![]() と
と![]() および
および
![]() が
同時に成立せざるを得ないことであり,
それで正の塑性ひずみ増分が発生する(
が
同時に成立せざるを得ないことであり,
それで正の塑性ひずみ増分が発生する(![]() )ためには,
必然的に
)ためには,
必然的に
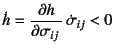 が成立するような
応力増分
が成立するような
応力増分
![]() が生じる必要がある。
こうなっていれば,ここで示した枠組の中であっても
が生じる必要がある。
こうなっていれば,ここで示した枠組の中であっても![]() による問題は生じない。
しかし,
による問題は生じない。
しかし,
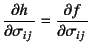 であることから,
「載荷」の条件が
であることから,
「載荷」の条件が
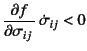 になってしまい,
「除荷」の判定と区別がつかない。
ということは,式(9.64)は
になってしまい,
「除荷」の判定と区別がつかない。
ということは,式(9.64)は
とでも定義し直す必要があるのかもしれない。
あるいは,式(9.78)の![]() の表現を用いて
の表現を用いて
とすれば,軟化の場合にも対応できるとする考え方(単に![]() の
条件だから本質的な解決ではないと思うが)もあるようだ。
の
条件だから本質的な解決ではないと思うが)もあるようだ。![]() は
弾性係数であり,
は
弾性係数であり,
![]() は適合な総ひずみ増分である。
ただし,式(9.78)の
は適合な総ひずみ増分である。
ただし,式(9.78)の
![]() を必須条件とする。
この必須条件は,上でも述べたように,負の
を必須条件とする。
この必須条件は,上でも述べたように,負の![]() を許容している。
いずれにしても数値解析では,載荷を仮定して計算して
求められる
を許容している。
いずれにしても数値解析では,載荷を仮定して計算して
求められる
![]() ,
,
![]() を用いて,
その仮定が正しいか否か判定せざるを得ないのだろう。
を用いて,
その仮定が正しいか否か判定せざるを得ないのだろう。
最も基本的な一般化されたPrandtl-Reussモデルを例に用いると
と定義されている。ただし,しばらくは硬化係数![]() は定数とする。これから
は定数とする。これから
であり,載荷条件は
と表される。また流れ則と整合条件から
という関係になる。
簡単な例として,2次元応力状態で
であり続ける場合を考えてみよう。
これは,薄肉円管を引張りながらねじる実験を想定すればいい。
このとき弾性は式(9.40)のHookeの法則から
となる。また,直応力成分の偏差成分は
であることから,まず式(9.84)から相当応力は
となり,載荷条件は式(9.85)から
となる。
さらに式(9.86)の流れ則は,
この載荷条件式(9.90)が成立しているとき
という関係であることを意味する。
ちなみに,流れ則は
が成立することを意味している。
これはかなり特殊な制約条件に感じられる。
また![]() か
か![]() のいずれかが零であり続けるような
単純な1次元応力状態の場合には,それぞれ
のいずれかが零であり続けるような
単純な1次元応力状態の場合には,それぞれ
となる。
式(9.91)を式(9.84)に代入すれば,
載荷が継続する限りは
となることから,これは載荷が継続する限り積分できて
となることから,式(9.84)の降伏条件に一致する。
ところで,式(9.91)の流れ則は
のように書くことができる。
ここで載荷が継続されているとした場合,もし
が成立すれば,この流れ則は積分可能(完全な全微分表現)になり,
積分経路に依存せずに塑性ひずみが唯一に求められることになる。
そこで,この各係数の微係数を求めてみると
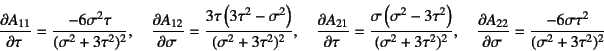
となることから,上の条件式(9.96)は満足されない。
これが式(9.42)の具体例である。
つまり,除荷をしない場合であっても
流れ則は一般には積分可能ではないことを意味し,
最終状態の応力が同じであっても,
そこまでの応力履歴が異なれば最終的な変形状態は違ってくる。
これが弾性と塑性の違いの中で最も重要な特性[51]だろう。
あるいは相当応力が非零のまま,式(9.96)が
成立するためには,第1式からは![]() ,
第2式からは
,
第2式からは![]() でなければならず,1次元応力状態の場合には
積分可能であり履歴依存が無いこともわかる。
でなければならず,1次元応力状態の場合には
積分可能であり履歴依存が無いこともわかる。
では,載荷が継続されているとした場合に,
式(9.95)の流れ則の逆関係を求めてみよう。
この係数行列の行列式が零であることから,解は存在しないか唯一には
決まらないかのいずれかである。
そこでp.![]() で述べたAlternative Theoremを
適用しよう。まず
で述べたAlternative Theoremを
適用しよう。まず
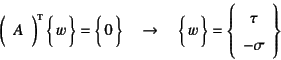
であることから,解が存在するための適合条件は
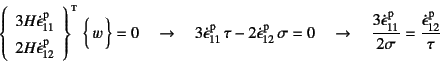
となり,式(9.92)の流れ則が成立する限りは,
この方程式には解が存在することがわかる。
そこで,斉次解が
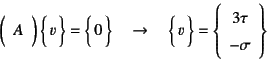
であり,式(9.92)の流れ則が満足するなら,
特解が1次元状態を仮定したときの
関係式(9.93)そのものの
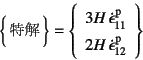
でいいことから,最終的に一般解が
と求められる。
この逆関係式(9.97)は,![]() の表現には左右されるが,
あたかも積分可能な式に見える。
ちなみに式(9.90)に代入すれば明らかなように,
この
の表現には左右されるが,
あたかも積分可能な式に見える。
ちなみに式(9.90)に代入すれば明らかなように,
この![]() の係数を持つ斉次解の部分は
中立載荷
の係数を持つ斉次解の部分は
中立載荷
![]() に相当する解である。
ということは上式(9.97)が
に相当する解である。
ということは上式(9.97)が
であることを意味している。
数学は面白いでしょ。
![]() なので,
比例載荷だけではない降伏曲面の外向きの任意の方向を向いた応力増分が
可能である。
なので,
比例載荷だけではない降伏曲面の外向きの任意の方向を向いた応力増分が
可能である。
この![]() を決定するために,式(9.97)を
降伏条件式(9.84)に代入してみる。
つまり
を決定するために,式(9.97)を
降伏条件式(9.84)に代入してみる。
つまり
(9.98)
の2式に式(9.97)を代入して,増分の2次項を
無視せずに,
![]() を消去して整理すると
を消去して整理すると
となる。式(9.92)の流れ則が成立していれば
左辺第1項の中の![]() の係数は零になる。また左辺第2項の括弧の中は
式(9.94)の相当塑性ひずみ増分の2乗なので,
右辺とキャンセルする。
したがってこの式は
の係数は零になる。また左辺第2項の括弧の中は
式(9.94)の相当塑性ひずみ増分の2乗なので,
右辺とキャンセルする。
したがってこの式は
と整理される。
左辺第1項に式(9.91)を代入すれば,
塑性仕事の恒等式
が成立することから右辺と一致するのでキャンセルされ,
最終的に降伏条件からは
が成立しなければならず,括弧の中は相当応力そのもので非零なので
結局
が唯一の解になる。したがって,
載荷が継続されているとした場合には,
式(9.97)から
が成立してしまう。これは1次元応力状態の解の
式(9.93)に一致し,積分可能になる。
さらにこの式と流れ則の式(9.92)から塑性ひずみ増分を
消去すると,それは
となる。
つまり,整合条件と増分の2次項も含めた降伏条件とを
両方とも厳密に満足させたまま継続した載荷を保持するためには,
線形硬化の場合の比例載荷しかあり得ないことを意味する。
実際,式(9.101)から
![]() ,
,
![]() と置いて
式(9.91)に代入すれば,式(9.100)を得る。
と置いて
式(9.91)に代入すれば,式(9.100)を得る。
最も単純な純せん断の場合には,![]() としておけばいいので,
流れ則と相当応力は
としておけばいいので,
流れ則と相当応力は
となる。一方,Hookeの法則式(9.88)からは
であるから,総ひずみ増分は
となる。もし![]() のまま載荷状態が継続している場合には簡単に積分できて,
工学ひずみで表すと
のまま載荷状態が継続している場合には簡単に積分できて,
工学ひずみで表すと
という関係が成立する。
あるいは逆関係が
となるので,図-9.23のようになる。 このような単純な場合には 流れ則が積分できてしまうため,図-9.9や 式(9.10)の全ひずみ理論と 増分理論が同じ結果をもたらすことは明らかである。
後述の式(9.158)に相当する
で表される硬化則の場合を考えておこう。 この場合も式(9.94)の相当塑性ひずみ増分は積分できて, 上式(9.102)を得る。 ただ式(9.91)の塑性ひずみ増分は この場合も一般には積分可能ではないことから,履歴依存性を持つことになる。
ただし純せん断の場合には,この場合であっても,
前節同様に積分可能で簡単な関係式が得られる。
具体的に式を展開すると結局
となるので,右図-9.24のような関係を得る。
初期降伏の状態では,弾性の直線部分と硬化後の曲線部分の
勾配は一致して滑らかに連続した関係を得る。
具体的な例を図-9.46にいくつか示したが,
パラメータ![]() の定義が若干違っていて,
さらにその図では横軸が相当塑性ひずみである。
の定義が若干違っていて,
さらにその図では横軸が相当塑性ひずみである。
さて,式(9.94)で相当塑性ひずみ増分が算定できたとして,
それが降伏条件式(9.98)を満足するかどうか
確かめておこう。
式(9.98)の2式に式(9.94)を
代入して
![]() を消去すると
を消去すると
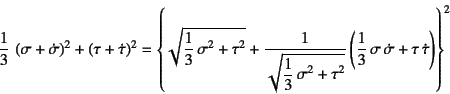
となる。この演算を続けると,最終的に
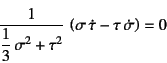
となり,結局,厳密に降伏条件が成立するためには
でなければならない。
つまり,式(9.101)の比例載荷条件に一致する。
逆に言うと,応力比率が比例条件を満足しない場合には,
載荷を連続させたとしても増分の2次項を
無視しない降伏条件式を厳密に満足させることは不可能である。
そもそも流れ則が積分不可能である以上,
塑性ひずみは増分の累積としてしか求めることができないから,
結局,任意の数値解析において応力やひずみを求めるためには,
現配置の各変数にその増分を加算し続ける計算をせざるを得ない。
それは増分が十分に小さいことを要請していることから
整合条件式(![]() )を真の関係式だと認めていいのだから,
降伏条件式を厳密には成立させ続けることは不可能になる。
)を真の関係式だと認めていいのだから,
降伏条件式を厳密には成立させ続けることは不可能になる。
これは,整合条件式(![]() )が降伏条件の全微分であり,
増分の2次項を無視したものであるにも拘らず,
上では2次項も含めた降伏条件を確認しようとしたことが原因なのである。
そこで,更新された相当応力に含まれる応力増分の2次項を無視して
)が降伏条件の全微分であり,
増分の2次項を無視したものであるにも拘らず,
上では2次項も含めた降伏条件を確認しようとしたことが原因なのである。
そこで,更新された相当応力に含まれる応力増分の2次項を無視して
と近似しておく。
この右辺に式(9.94) (9.98)を
代入すると,式(9.99)等を用いれば
となり,線形項のみを用いて降伏条件が厳密に成立することがわかる。
この線形項のみの降伏条件式(9.104)に
一般解の式(9.97)を代入すると結局![]() は任意でよく,
前述のように載荷方向のすべての応力増分解が可能になり,
つり合いから
は任意でよく,
前述のように載荷方向のすべての応力増分解が可能になり,
つり合いから![]() を求めることになる。
面白いことに,式(9.97)と元の流れ則の
式(9.91)あるいは式(9.92)とからは
を求めることになる。
面白いことに,式(9.97)と元の流れ則の
式(9.91)あるいは式(9.92)とからは
と表すことができる。
そして前節の結果のように,増分の非線形項も含めて降伏条件を満足させる
場合の条件である
![]() は確かに比例載荷に相当する。
は確かに比例載荷に相当する。
非線形項を含む降伏条件を繰り返し計算で解く手続きをした上で, 整合条件を用いた接線剛性を修正子の接線勾配として取り扱うことの 是非については後述するが,次のようにも考えている。 そもそも塑性論は流れ則が積分不可能な増分型で表されるし, 整合条件式の誘導からも明らかなように, その増分は十分に小さいことを前提としている。 したがって,降伏条件は厳密には成立しないものの,比例載荷以外の 任意の載荷パターンにおいても増分解析で十分なのである。 小さくない増分を用いたときの具体的な誤差の程度については, 以下の例で定量的に示しておこう。
普通鋼を念頭に置いて,![]() GN/m
GN/m![]() ,
, ![]() ,
,
![]() ,
,
![]() MPaとする。
載荷パターンは図-9.25に示したような3種類とする。
つまり,いずれも初期降伏までの載荷は比例で
MPaとする。
載荷パターンは図-9.25に示したような3種類とする。
つまり,いずれも初期降伏までの載荷は比例で
![]() とし,
比例載荷(prop)の場合はそのままの比率で最終応力状態
とし,
比例載荷(prop)の場合はそのままの比率で最終応力状態
![]() まで硬化させた。
比較する他の二つの載荷パターンは,応力状態が
まで硬化させた。
比較する他の二つの載荷パターンは,応力状態が
![]() の初期降伏から
の初期降伏から![]() か
か![]() の
片方を最終応力の
の
片方を最終応力の
![]() (s2t)か
(s2t)か
![]() (t2s)まで
載せた後,もう片方を最終応力まで載せた。
比例係数の
(t2s)まで
載せた後,もう片方を最終応力まで載せた。
比例係数の![]() は,二つの成分がほぼ同程度になる
場合を
は,二つの成分がほぼ同程度になる
場合を
![]() とし,
同程度ではない場合をその十分の一と10倍に設定した。
初期降伏時の応力と最終応力を
それぞれの
とし,
同程度ではない場合をその十分の一と10倍に設定した。
初期降伏時の応力と最終応力を
それぞれの![]() に対して表-9.1に示した。
に対して表-9.1に示した。
| ひずみ成分 | prop-ortional | t2s: torsion-to-stretch | s2t: stretch-to-torsion | |
| 11.148 | 10.688 ( |
11.584 (3.9%: 1.6%) | ||
|
|
9.6295 | 10.007 (3.9%: 1.4%) | 9.2310 ( |
|
|
|
26.777 | 26.777 | 26.777 | |
| 12.271 | 12.263 ( |
12.278 (0.057%: 0.034%) | ||
|
|
1.0593 | 1.1275 (6.4%: 0.33%) | 0.99390 ( |
|
|
|
20.848 | 20.848 | 20.848 | |
| 2.0957 | 1.8840 ( |
2.3226 (11%: 0.63%) | ||
|
|
18.113 | 18.130 (0.094%: 0.047%) | 18.092 ( |
|
|
|
35.923 | 35.923 | 35.923 |
初期降伏からのステップ数![]() を
を![]() (`t2s'と`s2t'では
(`t2s'と`s2t'では![]() )で
解析した総ひずみのひずみ成分と
相当塑性ひずみの結果を表-9.2に示した。
相当塑性ひずみは,その増分が積分可能な表現だったこともあり,
最終状態でいずれも同じ値に達しているものの,
それぞれの総ひずみ成分は履歴依存のために異なったレベルに達している。
括弧内のコロンの前の数値は,
比例載荷の場合の各ひずみ成分値に対する履歴依存による増減差の比率である。
ここでは10%という大きなひずみレベルまで計算したから
このような差が出ている。
これに対しコロンの後の比率は,各ひずみ成分値の増減差の
相当塑性ひずみ値に対する比率である。
応力比が
)で
解析した総ひずみのひずみ成分と
相当塑性ひずみの結果を表-9.2に示した。
相当塑性ひずみは,その増分が積分可能な表現だったこともあり,
最終状態でいずれも同じ値に達しているものの,
それぞれの総ひずみ成分は履歴依存のために異なったレベルに達している。
括弧内のコロンの前の数値は,
比例載荷の場合の各ひずみ成分値に対する履歴依存による増減差の比率である。
ここでは10%という大きなひずみレベルまで計算したから
このような差が出ている。
これに対しコロンの後の比率は,各ひずみ成分値の増減差の
相当塑性ひずみ値に対する比率である。
応力比が
![]() の場合に,
この差が相対的に大きく1.4〜1.7%程度となっているのは,
応力レベルが高いからである。
応力比が
の場合に,
この差が相対的に大きく1.4〜1.7%程度となっているのは,
応力レベルが高いからである。
応力比が
![]() と
と
![]() の場合にはそれが小さいことから,履歴依存性
は高めの多軸応力状態の場合に顕著になることがわかる。
ここの例では線形硬化を対象としたことから,両方の増減差比率とも,
半分の最終応力レベルまでの載荷では半分になるし,
一桁小さい最終応力レベルまででは一桁小さくなる。
重要なのは,履歴に依存して到達する変形状態が違ってくるということである。
の場合にはそれが小さいことから,履歴依存性
は高めの多軸応力状態の場合に顕著になることがわかる。
ここの例では線形硬化を対象としたことから,両方の増減差比率とも,
半分の最終応力レベルまでの載荷では半分になるし,
一桁小さい最終応力レベルまででは一桁小さくなる。
重要なのは,履歴に依存して到達する変形状態が違ってくるということである。
また念のために,応力に増分応力を加算したものを2乗して,
増分の非線形項も含めた降伏条件式(9.98)を算定してみると,
比例載荷の場合には数値解析上でも厳密に
(数値的には倍精度計算で![]() そのものが
そのものが![]() 程度以下,
つまり初期降伏応力との相対誤差で
程度以下,
つまり初期降伏応力との相対誤差で![]() 以下だから事実上零)成立する。
これに対し,例えば
以下だから事実上零)成立する。
これに対し,例えば
![]() の比例載荷ではない
場合には,
の比例載荷ではない
場合には,![]() の値と初期降伏応力の比で
定義した相対誤差の累積の仕方が図-9.26のようになる。
応力状態が
の値と初期降伏応力の比で
定義した相対誤差の累積の仕方が図-9.26のようになる。
応力状態が
![]() から
から
![]() までを
までを![]() で
(相当塑性ひずみで大きめな300
で
(相当塑性ひずみで大きめな300![]() 程度の増分でも)解析すれば,
このような単純な増分解析でも,6桁は精度が確保できている。
もちろん
程度の増分でも)解析すれば,
このような単純な増分解析でも,6桁は精度が確保できている。
もちろん![]() のように増分を大きくしてしまうと累積誤差は大きくなるが,
それでも3桁程度の精度は得られている。
しかも,載荷パターンが変化しない間は誤差の累積が次第に遅くなる。
しかし,載荷パターンが急変するとまた累積が急増している。
この結果は
のように増分を大きくしてしまうと累積誤差は大きくなるが,
それでも3桁程度の精度は得られている。
しかも,載荷パターンが変化しない間は誤差の累積が次第に遅くなる。
しかし,載荷パターンが急変するとまた累積が急増している。
この結果は
![]() の場合も同様だった。
何度も書くが,
そもそも増分理論の基本的な前提は,増分非線形性を無視することであり,
したがって
の場合も同様だった。
何度も書くが,
そもそも増分理論の基本的な前提は,増分非線形性を無視することであり,
したがって![]() は厳密には満たされなくとも,
整合条件式
は厳密には満たされなくとも,
整合条件式![]() によってそれを保証しようとするものである。
そのため繰り返し計算が必要な箇所は無くなり,
非線形的な履歴が,十分に小さい増分を用いて容易に精度良く追跡できている。
によってそれを保証しようとするものである。
そのため繰り返し計算が必要な箇所は無くなり,
非線形的な履歴が,十分に小さい増分を用いて容易に精度良く追跡できている。
少し現実的な場合の例として高張力鋼のような設定,
つまり硬化係数と初期降伏応力が高い場合を計算しておこう。
弾性特性は前の例と同じにした上で,
![]() ,
,
![]() MPaとした。
履歴依存度が他の場合より大きくなる
応力比
MPaとした。
履歴依存度が他の場合より大きくなる
応力比
![]() の場合のみを対象としたので,
初期降伏時の応力が
の場合のみを対象としたので,
初期降伏時の応力が
![]() となり,
最終状態は前例よりも少し現実的に相当塑性ひずみが約2%を目標として,
最終応力を
となり,
最終状態は前例よりも少し現実的に相当塑性ひずみが約2%を目標として,
最終応力を
![]() とした。
結果を表-9.3に示した。
前例よりも一桁小さい2%程度の塑性変形までで既に,
相当塑性ひずみを基準とした比率で1.5%程度と,
前例と同じ程度の履歴依存による差が発生している。
とした。
結果を表-9.3に示した。
前例よりも一桁小さい2%程度の塑性変形までで既に,
相当塑性ひずみを基準とした比率で1.5%程度と,
前例と同じ程度の履歴依存による差が発生している。
さて,降伏条件を厳密には満足させられないことに対する疑問や 不満・不安が生じたことだろう。 特に数値解析が容易に可能になると,この程度の非線形性の取り扱いには ほとんど問題が無いと思われる。 そこで,整合条件を用いることなく,降伏条件を非線形項まで 含めて満足させるような解析を試みてみよう。 多分,return-mapping法[67]を使う人達の中では こういった方法が標準になっていると予想される。 ただしこの節では,材料定数等は最初の例と同じとし, 線形硬化の場合を例示する。べき乗則硬化の例は後述する。
となる。これを式(9.94)に代入すると
を得る。一方,Hookeの法則式(9.88)と
上式(9.105)から
が成立する。
そこで,現時点の降伏条件と増分後の降伏条件式(9.98)からは
という関係が成り立つので,
これに式(9.106) (9.107)を
代入することによって
![]() に対する2次方程式を
に対する2次方程式を
のように得ることができる。 これを増分毎に解いていけば,整合条件を用いることなく,厳密に (数値解析上は誤差があっても)降伏条件を満足させた解析ができる。
ちなみに整合条件式は,
式(9.98a)の両辺の平方根を用いて
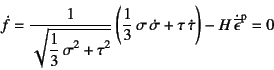
と書けるので,式(9.106) (9.107)を
代入することによって
![]() に対する1次方程式が
に対する1次方程式が
のように得られる。当然これは,
上式(9.108)に
含まれる
![]() とひずみ増分の非線形項を無視して
得られる
とひずみ増分の非線形項を無視して
得られる![]() の
線形式
の
線形式
![]() に一致する。
これに対し,式(9.108)を例えばNewton-Raphson法で
解く場合の修正のための接線係数は
に一致する。
これに対し,式(9.108)を例えばNewton-Raphson法で
解く場合の修正のための接線係数は
![]() で
あることから,整合条件を用いて算定される下の式(9.110)の
物理的な接線係数は,
非線形項を含めた降伏条件式をNewton-Raphson法で満足させるための
数値解析的に適切な(あるいは便宜的な)接線係数にはなっていないことが明らかだ。
で
あることから,整合条件を用いて算定される下の式(9.110)の
物理的な接線係数は,
非線形項を含めた降伏条件式をNewton-Raphson法で満足させるための
数値解析的に適切な(あるいは便宜的な)接線係数にはなっていないことが明らかだ。
ところで,最初の例の増分解析では応力増分を与えてひずみを求めて
議論したが,その逆も可能である。式(9.91)の
塑性ひずみ増分とHookeの法則式(9.88)から
と書くことができる。ここに
と定義したので,この式(9.109)の逆関係
から,ひずみ増分に対する応力増分を求めることができる。 この2式の係数行列が,式(9.87)の 応力状態における式(9.47)の具体例である。 この接線コンプライアンスと接線係数は増分理論の枠組における 弾塑性モデルの物理的な特性であり, 決してNewton-Raphson法で便宜的に用いられる数値解析的な量ではない。
最初の例と同じく大きな変形状態までの解析を試みるが,
載荷比
![]() の応力を与えた場合に
得られたひずみ値を与えて履歴の影響を考察しよう。
つまり,表-9.4にある初期ひずみ状態は
載荷比
の応力を与えた場合に
得られたひずみ値を与えて履歴の影響を考察しよう。
つまり,表-9.4にある初期ひずみ状態は
載荷比
![]() のときの初期降伏時のひずみ値であり,
最終ひずみ状態は表-9.2の
比例載荷時の最終応力時のひずみ値である。
さらに`t2s'と`s2t'の載荷時のパターン変更時点での
ひずみを中間ひずみ値
のときの初期降伏時のひずみ値であり,
最終ひずみ状態は表-9.2の
比例載荷時の最終応力時のひずみ値である。
さらに`t2s'と`s2t'の載荷時のパターン変更時点での
ひずみを中間ひずみ値
![]() として
設定した。これにより,除荷せず常に載荷条件が満足され続けるように
ひずみ増分を与えることができる。表-9.4の
整合条件を用いない結果は,
として
設定した。これにより,除荷せず常に載荷条件が満足され続けるように
ひずみ増分を与えることができる。表-9.4の
整合条件を用いない結果は,![]() 以上であれば完全に同じ結果になる。
これは線形硬化に設定したためである。この最終的に到達した応力に現れる
履歴依存の程度は5%前後と,表-9.2の結果と同様である。
なお,最終的に到達する全ひずみを同じにしたので,
累積される相当塑性ひずみ値は
若干異なっている。図-9.27に
応力ひずみ関係を示した。比例載荷ではない場合には軟化が生じて
除荷が発生しているようにも見えるが,
数値上は載荷条件が常に満足していた。
そこで確認のために,
降伏曲面と応力履歴を図-9.28に示した。
図では初期降伏後の履歴を拡大したが,図の右下の小さい図が
第1象限の降伏曲面図である。
このように,応力の変化は常に載荷方向を向いていることがわかる。
以上であれば完全に同じ結果になる。
これは線形硬化に設定したためである。この最終的に到達した応力に現れる
履歴依存の程度は5%前後と,表-9.2の結果と同様である。
なお,最終的に到達する全ひずみを同じにしたので,
累積される相当塑性ひずみ値は
若干異なっている。図-9.27に
応力ひずみ関係を示した。比例載荷ではない場合には軟化が生じて
除荷が発生しているようにも見えるが,
数値上は載荷条件が常に満足していた。
そこで確認のために,
降伏曲面と応力履歴を図-9.28に示した。
図では初期降伏後の履歴を拡大したが,図の右下の小さい図が
第1象限の降伏曲面図である。
このように,応力の変化は常に載荷方向を向いていることがわかる。
これに対し,単純な増分解析をした場合の結果を表の下半分に載せておいた。
比例載荷パターンではない`t2s'や`s2t'の場合,![]() の増分解析でも
解が4桁の精度を得ていることは,図-9.26の
降伏条件に含まれる誤差のオーダーの結果と整合している。
これは各ステップのひずみ増分を1000
の増分解析でも
解が4桁の精度を得ていることは,図-9.26の
降伏条件に含まれる誤差のオーダーの結果と整合している。
これは各ステップのひずみ増分を1000![]() 程度に設定した増分解析に相当する。
なお
程度に設定した増分解析に相当する。
なお![]() くらいの大きなひずみ増分を与えた場合には,
ある増分ステップ時に除荷条件になってしまい,数値解析が不安定になった。
しかし再度記しておくが,
弾性や流れ則等の構成則は増分についての線形関係のみでモデル化9.29しているのに対し,
降伏条件を満足させるために式(9.108)では
増分の2次項を厳密に算定しようとしている。これは増分の取り扱い方にバランスを欠いた考え方になってしまっている。
結果的に増分解析でも十分な精度が得られる以上,
降伏条件を厳密に満足させるような繰り返し計算・非線形計算をすることは,
力学的な観点からは必ずしも妥当なものとは思えない。
言い換えると,
整合条件を満足させながら降伏条件を厳密に満足させようとする解析は,
増分の取り扱いが異なる二つの降伏条件を同時に満足させようとしており,
厳密には数学的にもおかしなものである。
くらいの大きなひずみ増分を与えた場合には,
ある増分ステップ時に除荷条件になってしまい,数値解析が不安定になった。
しかし再度記しておくが,
弾性や流れ則等の構成則は増分についての線形関係のみでモデル化9.29しているのに対し,
降伏条件を満足させるために式(9.108)では
増分の2次項を厳密に算定しようとしている。これは増分の取り扱い方にバランスを欠いた考え方になってしまっている。
結果的に増分解析でも十分な精度が得られる以上,
降伏条件を厳密に満足させるような繰り返し計算・非線形計算をすることは,
力学的な観点からは必ずしも妥当なものとは思えない。
言い換えると,
整合条件を満足させながら降伏条件を厳密に満足させようとする解析は,
増分の取り扱いが異なる二つの降伏条件を同時に満足させようとしており,
厳密には数学的にもおかしなものである。
式(9.102)のべき乗則の場合には,
その非線形硬化の影響でさらに載荷の順番の影響が大きく現れそうだ。
そこで![]() MPa,
MPa, ![]() ,
,
![]() MPaの場合を
数値解析しておこう。
まず
MPaの場合を
数値解析しておこう。
まず![]() であることから,
であることから,
![]() が零のときに
硬化係数が無限大になる。
数値解析でこれを避けるために,ある小さい数値
が零のときに
硬化係数が無限大になる。
数値解析でこれを避けるために,ある小さい数値![]() を
零とみなし
を
零とみなし
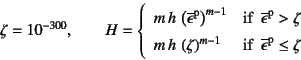
とした。 最初の線形硬化の例と異なり,前出の高張力鋼を念頭に置いた 例と同様少し大きめの降伏応力と硬化を設定したため, 最終的な変形状態は相当塑性ひずみで1%程度を目標とする。 したがって,表-9.5に示したような 初期降伏応力状態から最終状態までの載荷とした。
まず,二つの応力がほぼ同じレベルにある
![]() の
場合を増分解析しておこう。
べき乗則の場合には一般に,
比例載荷であっても降伏条件を厳密に
満足させることができない。図-9.29には,
比例載荷で累積する降伏条件の誤差を示した。
ステップ数が小さい場合には3桁の精度も得られていない。
特に硬化係数が大きい初期降伏直後の誤差の累積が大きい。
したがって実際のシミュレーション等では
かなり小さい荷重増分を設定せざるを得ないが,
この降伏条件に生じる誤差が許容範囲に入るように
荷重増分等を適切にコントロールしながら与えればいいだけのことである。
の
場合を増分解析しておこう。
べき乗則の場合には一般に,
比例載荷であっても降伏条件を厳密に
満足させることができない。図-9.29には,
比例載荷で累積する降伏条件の誤差を示した。
ステップ数が小さい場合には3桁の精度も得られていない。
特に硬化係数が大きい初期降伏直後の誤差の累積が大きい。
したがって実際のシミュレーション等では
かなり小さい荷重増分を設定せざるを得ないが,
この降伏条件に生じる誤差が許容範囲に入るように
荷重増分等を適切にコントロールしながら与えればいいだけのことである。
| 載荷パターン | ひずみ成分 | ||||||
| .78875 ( |
.87537 | .88629 | .88754 | .88768 | 0.88770 | ||
| prop | .63808 ( |
.71309 | .72255 | .72364 | .72376 | 0.72377 | |
|
|
.97744 ( |
1.1896 | 1.2164 | 1.2194 | 1.2198 | 1.2198 | |
| .80450 ( |
.84950 | .85487 | .85548 | .85555 | 0.85556 [ |
||
| t2s | .69787 ( |
.74264 | .74800 | .74860 | .74867 | 0.74868 [3.4%] | |
|
|
1.0849 ( |
1.2038 | 1.2180 | 1.2196 | 1.2198 | 1.2198 | |
| .85780 ( |
.90949 | .91567 | .91637 | .91645 | 0.91646 [3.2%] | ||
| s2t | .65172 ( |
.69069 | .69534 | .69587 | .69593 | 0.69593 [ |
|
|
|
1.0849 ( |
1.2038 | 1.2180 | 1.2196 | 1.2198 | 1.2198 |
さて,それぞれのステップ数毎の,
最終状態のひずみ成分の値を表-9.6に示した。
まずステップ数の影響を見るために3列目にある
普通の括弧に入れた相対誤差の比率を見ると,
どの載荷パターンにおいても![]() の結果は
の結果は![]() の値の5%以上の
誤差になっており,図-9.29の結果と整合する。
比例載荷(prop)の場合のステップ数の影響を
具体的な応力ひずみ関係の図-9.30に,
黒丸が最終状態の三つの曲線で示したが,
細い実線の
の値の5%以上の
誤差になっており,図-9.29の結果と整合する。
比例載荷(prop)の場合のステップ数の影響を
具体的な応力ひずみ関係の図-9.30に,
黒丸が最終状態の三つの曲線で示したが,
細い実線の![]() の場合の結果はほとんど
の場合の結果はほとんど![]() の太い一点鎖線の結果に
重なっている。
これは,ここで設定した材料定数の場合に
応力増分を30kPa程度以下にする必要があることを示している。
その10倍の大きめの増分を用いた
の太い一点鎖線の結果に
重なっている。
これは,ここで設定した材料定数の場合に
応力増分を30kPa程度以下にする必要があることを示している。
その10倍の大きめの増分を用いた![]() の場合も細い一点鎖線で示したが,
あるモデルを用いた数値シミュレーションにおいて,
この差はそれほど問題があるというわけでもない。
の場合も細い一点鎖線で示したが,
あるモデルを用いた数値シミュレーションにおいて,
この差はそれほど問題があるというわけでもない。
一方,履歴依存性について比べるために表-9.6の
右端の列にある鉤括弧に入れた相対誤差の比率を見ると,
比例載荷に対してそうでない二つの載荷パターンで3%程度の差が生じている。
ただし,やはり相当塑性ひずみ増分は積分可能であったことから,
履歴に依存しない値を得ている。![]() の結果を用いた
応力ひずみ関係を同じ図-9.30に示した(
`t2s'が□までの実線で,`s2t'が○までの破線)が,
相対誤差では3%程度ではあるものの,図で明確に判別できる程度の
履歴依存性が1%程度のひずみレベルで生じている。
応力比が
の結果を用いた
応力ひずみ関係を同じ図-9.30に示した(
`t2s'が□までの実線で,`s2t'が○までの破線)が,
相対誤差では3%程度ではあるものの,図で明確に判別できる程度の
履歴依存性が1%程度のひずみレベルで生じている。
応力比が
![]() ,
,
![]() の場合も,
ステップ数に対する誤差は
の場合も,
ステップ数に対する誤差は
![]() の例と
ほぼ同様であった。
の例と
ほぼ同様であった。![]() の
結果を図-9.31, 9.32に示したが,
塑性ひずみ増分が応力に比例するという流れ則の特性が顕著に現れている。
の
結果を図-9.31, 9.32に示したが,
塑性ひずみ増分が応力に比例するという流れ則の特性が顕著に現れている。
最後に,整合条件を用いることなく,増分の非線形項も考慮して
降伏条件を満足させる解析を行う。
式(9.105) (9.106)
(9.107)を式(9.102)の
降伏条件に代入して整理すると,
増分後の降伏条件が
![]() の関数として
の関数として
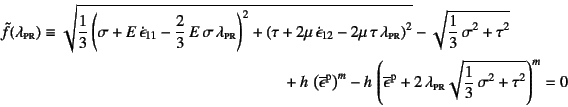
と表される。
これを標準的なNewton-Raphson法で解くと,第![]() ステップの修正計算と
収束判定は
ステップの修正計算と
収束判定は
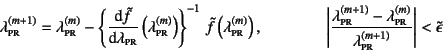
とすればいい。以下の計算では
![]() とした。
求めたい解
とした。
求めたい解
![]() が非常に小さい量なので,
が非常に小さい量なので,![]() が大きい場合に
この
が大きい場合に
この
![]() を小さくし過ぎると桁落ちのために収束しないことがある。
を小さくし過ぎると桁落ちのために収束しないことがある。
載荷は線形硬化の場合と同じようにした。 つまり,表-9.6の増分解析で得られた 比例載荷の初期降伏時から載荷を開始し, 同じく表-9.6の比例載荷の最終ひずみを最終状態とした。 また比例ではない載荷の場合は,パターン変更時のひずみを中間状態とした。 その値を表-9.7の上3行に示した。 もちろん表-9.6の増分解析では, べき乗則の非線形性によって, 二つのひずみ成分の増加の仕方は比例的でもなく線形でもなかったはずだが, ここではそれを線形的に与える。 したがって,応力の最終状態は表-9.6の結果とは異なる。
この表-9.7の
中ほどに,整合条件を用いずに得られた最終状態の応力成分を示した。
線形硬化の場合と異なり,少し多めのステップ数![]() を用いないと
精度が良くない。これは,Newton-Raphson法の繰り返し計算中にも
非常に小さいとはいえ履歴依存性が生じるためである。
つまり,理論的には厳密な計算はできないことを意味し,
ある程度は小さい増分を用いざるを得ない。
しかしもちろん,表の下半分にある単純な増分解析よりは,
少ないステップ数での精度がかなりいいことから,
実際のシミュレーションでは繰り返し計算を用いるメリットはありそうだ。
そこで,比例載荷時の繰り返し計算回数と相当塑性ひずみレベルの
関係を図-9.33に示した。
を用いないと
精度が良くない。これは,Newton-Raphson法の繰り返し計算中にも
非常に小さいとはいえ履歴依存性が生じるためである。
つまり,理論的には厳密な計算はできないことを意味し,
ある程度は小さい増分を用いざるを得ない。
しかしもちろん,表の下半分にある単純な増分解析よりは,
少ないステップ数での精度がかなりいいことから,
実際のシミュレーションでは繰り返し計算を用いるメリットはありそうだ。
そこで,比例載荷時の繰り返し計算回数と相当塑性ひずみレベルの
関係を図-9.33に示した。![]() が小さいときは,
繰り返し計算が10回程度は必要になることから,
が小さいときは,
繰り返し計算が10回程度は必要になることから,![]() ステップで
繰り返し計算を伴う解析の精度と
ステップで
繰り返し計算を伴う解析の精度と![]() ステップを
用いた単純な増分解析の精度とを比較することによって,
繰り返し計算のメリットを定量化できそうだ。
そのような観点で表-9.7の中ほどと
下半分の結果を比べると,
単純な増分解析でもそこそこいい結果が得られていることがわかる。
ステップを
用いた単純な増分解析の精度とを比較することによって,
繰り返し計算のメリットを定量化できそうだ。
そのような観点で表-9.7の中ほどと
下半分の結果を比べると,
単純な増分解析でもそこそこいい結果が得られていることがわかる。
さて表-9.7の8列目の 履歴依存による応力値の差は,表-9.6のひずみ値に 現れる差に比べてやや大きい。 実はこれは,前述のように載荷のパターン(応力を等増分で与えたか, ひずみを等増分で与えたかの違い)がこの二つの表の間で全く異なるからである。 得られた応力ひずみ曲線を図-9.34に示した。 比例載荷ではない場合には,この図だけを見ると線形硬化の場合と同様, 軟化が生じているように見え,除荷が生じているようにも見えるが, 計算上ではすべてのステップで載荷条件が成立していた。 このような載荷パターンであったため履歴依存が顕著に現れたのである。 また最終的に到達する全ひずみを同じにしたので, 累積される相当塑性ひずみ値は載荷パターン毎に若干違うが, その差は線形硬化の場合よりも顕著に なっている。図-9.35が 降伏曲面上の変化である。
最後に,単純な増分解析との精度の差を見るために,![]() の場合の
増分解析結果を細い線で同じ図に示したが,この程度の差しかなく,
モデルシミュレーションという工学的な目的のためにはそれほど問題になる
差にはなっていない。ちなみに,
の場合の
増分解析結果を細い線で同じ図に示したが,この程度の差しかなく,
モデルシミュレーションという工学的な目的のためにはそれほど問題になる
差にはなっていない。ちなみに,![]() の増分解析結果は
図上では
の増分解析結果は
図上では![]() の結果との区別がつかなかった。
これは与える増分ひずみが10
の結果との区別がつかなかった。
これは与える増分ひずみが10![]() 程度に相当する。
実際,表-9.7でも
程度に相当する。
実際,表-9.7でも![]() で5桁の有効数字の
精度が確保できていた。
で5桁の有効数字の
精度が確保できていた。
このように,増分理論を増分の非線形項を無視した枠組の理論体系だと 考える限りは,整合条件は降伏条件と同じ条件式と考える必要があり, また数値解析上も単純な増分解析が誤りであるわけではないことが 明らかである。 逆に,整合条件と,増分の非線形項を含めた降伏条件とのいずれをも 満足させようとする数値解析は,増分の扱いにアンバランスがあり, また同じ条件式を二種類の表現で同時に用いようとしている点で 問題があることもわかる。
ここでちょっと数理物理の世界で遊んでみよう。かく書く第1著者は全く
理解していないが,文献[55]にとても面白い記述がある。
それは節-3.5.3の二つ目の例でも示した数学的転位
の移動と塑性の関係を論じた部分である。Burgersベクトル
(結晶格子のずれ分量)が![]() の転位が
の転位が![]() 方向に伸びているとする。
この転位が伸びている方向の線を転位線
と呼ぶ。この転位線が外力の作用によって,速度
方向に伸びているとする。
この転位が伸びている方向の線を転位線
と呼ぶ。この転位線が外力の作用によって,速度![]() で
移動しつつあるとしよう。
このとき,この転位が移動したことによって生じる速度勾配(変形勾配の
変化)は
で
移動しつつあるとしよう。
このとき,この転位が移動したことによって生じる速度勾配(変形勾配の
変化)は
と9.30なる。ここに
![]() は式(3.26)で
定義した交代記号である。以下
は式(3.26)で
定義した交代記号である。以下
と定義するが,この![]() は転位密度と呼ばれている。
この転位によって生じる塑性ひずみ増分は,速度勾配の対称成分で
表すことができ
は転位密度と呼ばれている。
この転位によって生じる塑性ひずみ増分は,速度勾配の対称成分で
表すことができ
となる。このような塑性ひずみ増分が生じるときの塑性仕事増分と,
塑性的な体積ひずみ増分は,式(![]() ) (
) (![]() )から
)から
でなければならない。この2式が同時に成立するには,村は
でなければならないことを見出した。つまり,この式を上の2式に代入すると
となっていることがわかる。この![]() は,転位線に生じている
何らかの力(ん? 3階のテンソルの力って?震源と同じような偶応力?)であると
考えられている。
ちなみに,交代記号にはその定義から
は,転位線に生じている
何らかの力(ん? 3階のテンソルの力って?震源と同じような偶応力?)であると
考えられている。
ちなみに,交代記号にはその定義から
という関係があり,上式の誘導でも用いた。
式(![]() )の関係を,式(
)の関係を,式(![]() )に代入して
式(
)に代入して
式(![]() )を書き直すと
)を書き直すと
となり,これは![]() を
を![]() と読み替えれば,
式(9.30)の流れ則に他ならない。
また,転位線に生じている力
と読み替えれば,
式(9.30)の流れ則に他ならない。
また,転位線に生じている力![]() の大きさ(絶対値に相当する量)は
の大きさ(絶対値に相当する量)は
と,式(9.22a)の
![]() に一致する。
したがって,式(9.25)のMisesの降伏条件を満足する材料なら,
これが降伏せん断応力に一致する。
すなわち,降伏条件を満足した位置にある転位は移動し始め,
流れ則に従って体積変形の無い,
せん断の非可逆ひずみが生じるということになる。
いかがでしょう。ちょっと面白いような,知っている人が数学で遊んでいるような。
閑話休題。
に一致する。
したがって,式(9.25)のMisesの降伏条件を満足する材料なら,
これが降伏せん断応力に一致する。
すなわち,降伏条件を満足した位置にある転位は移動し始め,
流れ則に従って体積変形の無い,
せん断の非可逆ひずみが生じるということになる。
いかがでしょう。ちょっと面白いような,知っている人が数学で遊んでいるような。
閑話休題。