最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。

12.1 有限変形って?

英語で表現したときの`finite deformation'は， 微小変形`infinitesimal deformation'に対峙させたものであり， いわゆる「大」変形に相当すると習った。 「限りが有る」という意味ではないということだ。 多分，「大」変形`large deformation'という言葉 には材料の非線形性を必ず伴うような印象を与えることから， 区別しているとも推測される。 この章は，材料の抵抗則が線形か非線形かによらず，変位や変形（ひずみ）の 大きさに制限を設けない場合^12.1の定式化， つまり主に幾何学的な非線形性を保持した定式化について解説する。 ところで， 弾性座屈のように変位は大きくても変形（ひずみ）が大きいとは限らないし， 逆に，変形が大きい（非線形になる）場合に必ずしも変位が大きくなるとは 限らない。 このようなことから判断して，変位と変形は厳密に区別すべきであることには 留意して欲しい。 ただしこの章のタイトルは「有限変形」としたが， 変位もその大きさには制限を設けないものとする。 さて，この章のほとんどの記述では， 数学的な表現の正確さを保持しようとしているため，初学者は特に， 京谷孝史教授が文献[94]で述べているように数学と物理学の区別あるいは 対応を常に考えておく必要がある。 著者もこれは苦手なので，苦悩を伴う表現をあちこちに用いざるを得なくなっている。 しかし読者は，出てくる式の記号や表現に惑わされず， またその美しさの方に気を引かれることなく，常に物理的な意味を 頭の中に思い描き続けることが重要だ。 記号は，できるだけ標準的なものを用いたが， どうしても変更したいものについては通常とはかなり異なるものを用いている。 さらに，二つの異なる階数を持つ異なるテンソル量に対して同じ記号を 用いていることがあるが，文脈（式脈）を読み取って区別して欲しい。

ここでは， 文献[24]とそれを用いた西野教授の「応用弾性学」の 講義ノート（1975年頃）が基本にあって， それに加えてアメリカ合州国Illinois州Evanston, Northwestern大学Nemat-Nasser教授の`Continuum Mechanics'の講義ノート（1980年頃）と文献[59]を参考にした。 実は，このお二人の講義内容は，現在我が国で教えられている有限変形理論とは 若干異なる角度からそれを眺めているようなものになっていると感じている。 そのため，この章の内容は，既に有限変形理論を習得している読者には 違和感を感じるものになっている可能性が高い。 なお簡単のために，極力「テンソル」という言葉を使っていない。 また，直角座標での取り扱いに限定するので共変成分と反変成分の 区別をしていない。 というよりも，適当に使っているので， 特に大文字添え字の成分を持つテンソル量についてはその物理的な意味について 十分な注意が必要である。 正確なテンソル演算については付録-Jを参照して欲しい。 さらに，特に時刻（配置）を関数の引数(argument)に明記する必要が無い部分では， それを省略した。

記号: 簡単のためテンソルの積では，左辺・右辺共に同じ階数同士の演算では

$$\fat{A}=\fat{B}\fat{C}\quad\left(A_{ij}=B_{ik} C_{kj}\right... ...D}=\fat{S}\fat{Q}\quad\left(D_{ijkl}=S_{ijmn} Q_{mnkl}\right)$$

のように積の記号は省略し，そうでない場合には以下のような積の記号を用いる。

$$\begin{eqnarray*} && s=\fat{u}\fat{\cdot}\fat{v}\quad \left(s=u_j v_j\right), \... ...}=\fat{A}\otimes\fat{B}\quad\left(Q_{ijkl}=A_{ij} B_{kl}\right) \end{eqnarray*}$$

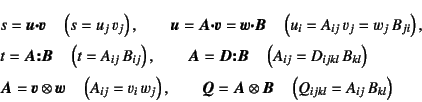
また，行列として扱う場合には括弧を用いる。

$$\matrx{A}=\matrx{B} \matrx{C}\quad \left(\fat{A}=\fat{B}\fat{C}, A_{ij}=B_{ik} C_{kj}\right)$$

最新版を正確に読むためには pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。