最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。

• G.2.1 逆問題の概念
• G.2.2 離散化

G.2 逆問題と境界要素法

G.2.1 逆問題の概念

全く理解していないので，おおまかな概念のみを記しておく。 興味を持った人は文献[101]を読んでください。 通常の順問題では，刺激$p$に対する応答$u$を求めようとする。 これに対し，逆問題 というのは，応答$u$から刺激$p$を推定しようとするのである。 広く知られている応用例は，内臓のエコー検査^G.1である。 皮膚に当てた装置からある種の波を体内に送り出し，反射してきた波から 得られるデータを処理し，内臓の大きさや血液の流速等を測定する検査である。 社会基盤構造の場合は，鋼橋の溶接部の亀裂を 超音波探査すること等の非破壊評価 がこれに当たる。 この概念を式(G.5)を用いて簡単に説明すると， 右辺第1項のみを取り出し

$$\dfrac12 \bar{u}(\fat{x})= \int_V G(\fat{x};\fat{\xi}) p(\fat{\xi})\dint\fat{x}$$ (G.6)

において，右辺の被積分関数の$p(\fat{x})$を，鋼中の亀裂や内臓を モデル化した散乱源と考える。これに物体表面から波を送る。 そして，左辺が物体表面のセンサーで測定した反射波のデータである。 そのデータを用いて，右辺の被積分関数の中の 散乱源$p(\fat{x})$を未知関数として解くのである。 この式(G.6)の積分方程式 を解いて$p(\fat{x})$を求める，つまり亀裂の大きさと場所， あるいは内臓の大きさ等を求めるというのが逆問題である。 積分方程式の例は，節-3.5.3 (2)にも示した。

G.2.2 離散化

式(G.5)が解ければ， 少なくとも境界での解を求めることができる。 一旦境界での解が決定されれば，その解を式(G.4)に 代入することによって， 領域内部任意点での解を求めることができる。したがって，何らかの方法を 用いて，この境界での値を求めることが第一である， というのが境界要素法 の目的となる。

境界要素法では，式(G.5)を有限要素法と同じように， ある関数を仮定することによって離散化し，その近似解を求めようとする。 つまり，未知関数$u(\fat{x})$をある既知関数と未定係数の積で与えるが， その未定係数としては物理的な意味のある，境界上での関数値を用いる。 一般的に記述すれば

$$u(\fat{x})=\sum_{i=1}^N u_i \phi_i(\fat{x}), \quad f(\fat{x... ... f_i \psi_i(\fat{x}) \quad \mbox{on  } \fat{x}\in \partial V$$

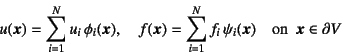
と書いてもいいだろう。ここでは境界面に$N$個の節点を設け， その点( $\fat{x}=\fat{x}_i$, $i=1,2,\cdots N$)での 未知関数の値$u_i$, $f_i$を係数とする関数を上式で与えたと考える。 あとは，この試行関数を式(G.5)に代入すればよく， それは

$$\dfrac12 u_i=\dfrac12 u(\fat{x}_i)= \sum_{j=1}^N\int_{\par... ...nt\fat{\xi} = \sum_{j=1}^N\left[B_{ij} f_j-A_{ij} u_j\right]$$ (G.7)

となる。簡単のために分布外乱$p$を省略した。ここに

$$A_{ij}\equiv \int_{\partial V} g(\fat{x}_i;\fat{\xi}) \phi... ...ial V} G(\fat{x}_i;\fat{\xi}) \psi_j(\fat{\xi})\dint\fat{\xi}$$

と定義した。 式(G.7)の左辺を右辺に移項して整理すると， 境界上での積分方程式が最終的に

$$\sum_{j=1}^N\left[B_{ij} f_j- \left(A_{ij}+\dfrac12 \delta_{ij}\right) u_j\right]=0$$ (G.8)

のような，離散化された代数方程式に変換できる。 ここに$\delta_{ij}$はKroneckerのデルタである。 与えられた境界条件の基でこの式を解けば， 境界上の$\fat{u}$を求めることができる。

最新版を正確に読むためには pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。