最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。

• G.1.1 問題の設定
• G.1.2 積分方程式

G.1 積分方程式への変換

G.1.1 問題の設定

これもよく，否，全く理解できていないトピックスであるが，1992年頃に 誰かに説明するために作った資料である。 そのあと，故北原道弘先生の授業「弾性波動論」を担当したときに， 文献[101]で勉強を試みたものの，挫折したトピックスである。 破壊力学とこの力学にはいまでも拒否反応しか感じない。

図 G.1: 解きたい問題と基本解

簡単のためにラプラス方程式を対象とする。

解きたい問題:

これは解こうとする境界値問題で

(G.1)

で与えられるものとする。

基本解の問題:

こちらは 無限領域の境界値問題で， $\fat{x}=\fat{\xi}$点に 集中外乱 (つまりデルタ関数) が作用した問題のことで

$$\nabla^2 G(\fat{x};\fat{\xi})+\delta(\fat{x}-\fat{\xi})=0, ... ... \mbox{with} \quad G \to 0 \quad\mbox{as} \quad x \to \infty$$ (G.2)

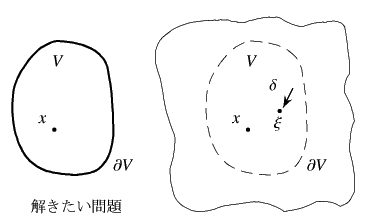
で与えられるものとする。 この基本解が，図-G.1右図の破線部分， つまり解きたい問題に相当する領域の境界部分($\partial V$)で

$$\fat{\nu} \fat{\nabla} G(\fat{x};\fat{\xi}) = g(\fat{x};\fat{\xi}) \qquad\qquad \mbox{on  }\partial V$$ (G.3)

のような関数値 $g(\fat{x};\fat{\xi})$を持つものとする。

G.1.2 積分方程式

この基本解を「仮想変位」と捉え，解きたい問題の仮想仕事式を求めよう。 式(G.1a)に式(G.2)の$G$を乗じて領域全体で 積分すると

$$0=\int_V G \left\{\nabla^2 u(\fat{x})+p(\fat{x}) \right\} \dint\fat{x}$$

が成立するはずだ。 そこで，被積分関数第1項にGaussの発散定理を2回適用すれば

$$\begin{eqnarray*} 0&=&\int_V G (u_{,kk}+p)\dint\fat{x} =\int_{\partial V} G (... ...fat{x} +\int_V G_{,kk} u\dint\fat{x} +\int_V p G\dint\fat{x} \end{eqnarray*}$$

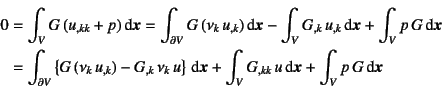
となるから，式(G.2)をこの第2項に代入すれば

$$\begin{eqnarray*} 0&=&\int_{\partial V} \left\{ G (\nu_k u_{,k}) -G_{,k} \nu... ...k u\right\}\dint\fat{x} -u(\fat{\xi}) +\int_V p G\dint\fat{x} \end{eqnarray*}$$

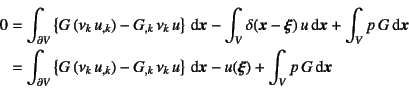
となり，最終的に

$$u(\fat{\xi})=\int_V p(\fat{x}) G(\fat{x};\fat{\xi})\dint\fa... ...fat{\nu} \fat{\nabla}G(\fat{x};\fat{\xi})\right\}\dint\fat{x}$$

という式が求められる。 これに，解きたい問題の境界条件式(G.1b)と 式(G.3)を代入すると

$$u(\fat{\xi})=\int_V p(\fat{x}) G(\fat{x};\fat{\xi})\dint\fa... ...) -\bar{u}(\fat{x}) g(\fat{x};\fat{\xi})\right\}\dint\fat{x}$$ (G.4)

という式を得ることができる。 この式は，領域内の任意点$\fat{\xi}$の解を

1. 分布外乱$p(\fat{x})$と基本解の仮想仕事（内積）と
2. 領域表面における，外乱$f(\fat{x})$と基本解の 仮想仕事，および，基本解の見かけ上の外乱と$u$との仮想仕事

の和で表したことになる。

そこで，式(G.4)の $\fat{\xi}\to\partial V$の 極限を考えると，この式の左辺は境界上の解 $\bar{u}(\fat{\xi})$ ( $x\in\partial V$)を求める式になるが，右辺の被積分関数にも 境界の解$\bar{u}$が含まれていることから，これは積分方程式 になる。ところが，その極限はそんなに簡単ではない。 つまり，基本解は

$$G(\fat{x};\fat{\xi}) \to \infty \quad \mbox{as} \quad \fat{x} \to \fat{\xi}$$

という特性を持っているからである。 したがって，この $\fat{\xi}\to\partial V$の極限では， 式(G.4)の積分は特異積分になってしまうことに 注意しなければならない。 この積分については文献[101]を勉強して欲しい。 結果だけを写すと

$$\dfrac12 \bar{u}(\fat{\xi})= \int_V p(\fat{x}) G(\fat{x};... ...) \right\}\dint\fat{x} \quad \mbox{on  }\fat{\xi}\in\partial V$$

となる（らしい）。 $$\fint$$はCauchyの 主値積分であることを指す。 元々の問題が自己随伴 であることから

$$G(\fat{x};\fat{\xi})=G(\fat{\xi};\fat{x}), \quad g(\fat{x};\fat{\xi})=g(\fat{\xi};\fat{x})$$

が成立する（相反定理）ので，上式は$\fat{x}$と$\fat{\xi}$を入れ替えて

$$\dfrac12 \bar{u}(\fat{x})= \int_V G(\fat{x};\fat{\xi}) p(... ...)\right\}\dint\fat{\xi} \quad \mbox{on  } \fat{x}\in\partial V$$ (G.5)

とも表現できる。 これが，境界の解$\bar{u}$を求める積分方程式として解釈できる。

最新版を正確に読むためには pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。