最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。

• 6.5.1 バネ支持された梁-柱の座屈
• 6.5.2 弾性床上の梁-柱の座屈
• 6.5.3 Timoshenko梁-柱の座屈
• 6.5.4 弾性床上のTimoshenko梁-柱の座屈

6.5 その他の梁-柱の座屈

6.5.1 バネ支持された梁-柱の座屈

図 6.45: 中央をバネ支持された梁-柱

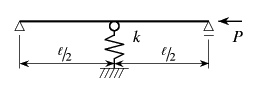
式(6.34)と図-6.23の座屈モードから わかるように，梁-柱の長さを 半分にすれば座屈荷重は4倍に上がる。図-6.29でも その効果を示したように， これを工学的に応用し，例えば途中に支点を設けることはできない梁の 中間に対傾構を配置する等の措置によって柔な支持点を設け， 梁を弾性的に支持させて 座屈強度を上げることを考えてみる。 そこで，図-6.45に示したように中央をバネで 支持された単純支持梁-柱の曲げ座屈を解いてみよう。

バネの左右の部分は式(6.30)の梁-柱の式で 支配されているから，その一般解は式(6.38)で 与えられる。境界条件は両端で$w=0$, $w''=0$であるから

$$w(x)= b x+c \sin\mu x \quad \left(0<x<\slfrac{\ell}{2}\ri... ...mu\xi \quad \left(0<\xi\equiv(\ell-x)<\slfrac{\ell}{2}\right)$$

が解の候補となる。四つの積分定数を $x=\slfrac{\ell}{2}$での 連続条件で決定すればいい。ここの連続条件は， 集中載荷点での条件式(4.44) (4.45)および図-6.28のバネ支持の境界条件式(6.43)を参考にすると

$$\begin{eqnarray*} && w(\slfrac{\ell}{2}-) = w(\slfrac{\ell}{2}+), \quad w'(\slf... ...t\{-EI w'''(\slfrac{\ell}{2}+)-P w'(\slfrac{\ell}{2}+)\right\} \end{eqnarray*}$$

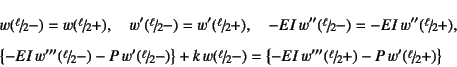
とならなければならないことがわかる。せん断力の連続条件にバネ支持の反力が 含まれていることに注意する。$x$と$\xi$に関する奇数階微係数の符号の 違いに注意すれば，上の一般解をこの条件に代入すれば

$$\left(\begin{array}{cccc} \ell & 2\sin\left(\frac{\mu\ell}{... ...=\left\{ \begin{array}{c} 0 0 0 0 \end{array}\right\}$$

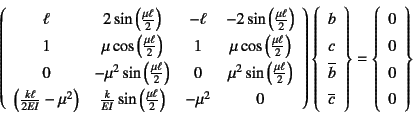
を得る。この係数行列が特異になる条件は

$$\sin\left(\frac{\mu\ell}{2}\right) \left[ \alpha_s \sin\l... ...ht)^3\right\} \cos\left(\frac{\mu\ell}{2}\right)\right]=0$$ (6.60)

となり，これが座屈荷重を与える特性方程式になる。ここに$\alpha_s$は 式(4.41)で定義したバネ剛性を代表するパラメータである。

面白いことに式(6.60)は常に

$$\sin\left(\frac{\mu\ell}{2}\right)=0 \quad\to\quad \dfrac{\mu \ell}{2}=\pi \quad\to\quad k_b=4$$ (6.61)

という解を与える。つまり，中央の バネによってそこを節とするsine 1波の座屈モードが常に可能である。 しかし，この荷重が必ずしも最小の座屈荷重であるとは限らない。 式(6.60)のもう一つの可能性は

$$\alpha_s \tan\left(\frac{\mu\ell}{2}\right)= \alpha_s\left... ...{\mu \ell}{2}\right) -16 \left(\dfrac{\mu \ell}{2}\right)^3$$ (6.62)

である。これも陽な表現にはなっていないので二つの特別な場合を まず検討しよう。最初は$\alpha_s\to 0$，つまりバネが無い 場合である。このときは$\mu \ell>0$なので上式は

$$\cos\left(\frac{\mu\ell}{2}\right)=0 \qquad\to\qquad \dfrac{\mu \ell}{2}=\dfrac{\pi}{2} \quad\to\quad k_b=1$$

つまりEuler荷重になるという当然の結果を得る。 次に $\alpha_s\to\infty$の場合，つまりバネ支持では なく普通の支承が配置された場合になるが，この解は

$$\tan\left(\frac{\mu\ell}{2}\right)=\frac{\mu\ell}{2}$$ (6.63)

となる。これは演習 問題6-2の3番の 片端固定・片端単純支持梁の座屈の特性方程式において， 梁の長さを半分にした式に一致する。 すなわち，バネ支持部でのたわみ角が零になるような反対称の座屈モードに 対応している。

図 6.46: 中央をバネ支持された梁-柱の座屈係数

特別な場合も含めて，以上の結果をバネ剛性と座屈係数の間の関係で まとめたのが図-6.46である。 まず$\alpha_s=0$付近では座屈係数が1に近い。 座屈モードも図中に示したようにsine半波に近い形をしていて， バネ支持の影響が小さい。 このパラメータ$\alpha_s$が $16\pi^2\simeq 157.9$より小さい場合には， 式(6.62)の解の方が最小の座屈荷重を 与える。しかし $\alpha_s=16\pi^2$になったとき， 式(6.61)と式(6.62)の座屈荷重が一致する。 つまり， $\alpha_s>16\pi^2$であるような 比較的剛なバネを配置すると，sine 1波の座屈モードで座屈することに なる。したがって，図中の実線で示した$k_b=4$が最初に発生する座屈荷重で ある。ちなみに，$\alpha_s$が非常に大きくなったときの 式(6.62)の解を求めると，座屈係数が$k_b=8.1815$に なる。このモードを図中右上に示しておいたが， 片端固定・片端単純支持の梁を二つ左右対称（反対称ではない）に 並べたモードの座屈である。 これが式(6.63)の場合に相当する。 このように，完全な支えではなくとも，ある程度の支えや拘束が中間にあると， その梁-柱の座屈荷重を上げることができる。 それはつまり，有効座屈長を短くしていると考えればわかり易い。 工学的にはとても重要な結果であり，座屈モードを知ることの重要性を示唆している。

図 6.47: 片端を回転バネ支持された柱の座屈

1. 図-6.47の二つの系の座屈荷重を求めよ。

6.5.2 弾性床上の梁-柱の座屈

図 6.48: 弾性床上の梁-柱の座屈

弾性床上に置かれた梁-柱の場合には，式(6.30)の 通常の梁-柱理論のつり合い式と式(4.86)の弾性床 上の梁のつり合い式とを比較すれば明らかなように

$$-EI w''''(x)-P w''(x)-k_w w(x)+q(x)=0$$ (6.64)

がそのつり合い式となる。 境界条件は通常の梁-柱の式(6.31)と同じだ。 例えば図-6.48に示したように，$q(x)\equiv 0$で 両端が単純支持された場合の座屈問題は， 通常の梁-柱の解法と同じように $w\sim\exp(\xi x)$を つり合い式に代入し，その特性方程式

$$EI \xi^4+P \xi^2+k_w=0$$

から特性根を計算すれば，一般解を得る。 境界条件に代入し，$w$が恒等的には零にならずに有意な解が 存在するための問題，つまり固有値問題として$P\sub{cr}$を探し出せば 座屈荷重を決定することができる。 詳細は省略するが，式(6.41)で定義された座屈係数が

$$k_b\equiv \dfrac{P\sub{cr}}{P\subsc{e}}=n^2+s_w \dfrac{1}{n^2\pi^4}$$ (6.65)

と求められる。ここに$P\subsc{e}$は式(6.35)で 定義したEuler荷重であり

$$s_w\equiv\dfrac{k_w\ell^4}{EI}$$ (6.66)

は弾性床の反力特性を代表するパラメータである。

通常の梁-柱の座屈では， 式(6.34)から明らかなように 第2次モードの座屈荷重は第1次座屈荷重の4倍も大きかった。 ところが式(6.65)の座屈荷重は，弾性床の反力係数に よっては$n=2$の座屈荷重の方が$n=1$の荷重より小さくなることもある。 例えば式(6.65)の$n=1$の座屈荷重が，$n=2$の 座屈荷重より大きくなるときのパラメータ$s_w$を計算すると

$$1+\dfrac{s_w}{\pi^4}>4+\dfrac{s_w}{4\pi^4} \quad\to\quad s_w>4\pi^4\simeq 390$$

となる。つまり$s_w\sim 400$程度になると，$n=2$のsine 1波の 座屈モードの座屈荷重( $k_b^{(n=2)}=5.03$)の 方が，sine半波の座屈モードのそれ( $k_b^{(n=1)}=5.11$)よりも 小さくなる。ちなみに$n=3$の場合は $k_b^{(n=3)}=9.46$であり，$n=1$, 2の 場合の2倍もは大きくならない。 つまり，弾性床の反力係数によっては， 相対的に短い周期の座屈モードに対する座屈荷重の方が最小値になり得る という，非常に興味深い性質を示している。

1. つり合い式(6.64)を誘導し， 座屈係数の式(6.65)を求めよ。

6.5.3 Timoshenko梁-柱の座屈

図 6.49: Timoshenko梁の座屈荷重

このように，弾性床上の梁-柱では 比較的短い波長モードの座屈が重要になる場合がありそうだ。 そうなると，梁-柱の全長が大きくても， その短い座屈モード波長に対する初等梁理論の適用性を少し検討する必要が出てくる。 つまり，初等梁理論は細長い棒で良い精度を与えてくれるだけだったから， このように比較的短い棒の曲げを対象とする 場合には，節-4.6.2で説明した せん断変形の影響も相対的に大きくなる可能性がある。 したがって，いわゆるTimoshenko梁理論を用いて座屈荷重を検討する必要が あるかもしれない。理論の誘導の詳細や計算手順については 文献[37]等^6.10を参照してもらうことにして割愛し， 両端単純支持の場合の座屈公式を挙げておく。 まずEngesserの公式 と呼ばれる理論の座屈係数は

$$k_b=\dfrac{1}{1+\alpha\subsc{t} \pi^2}$$ (6.67)

となり，その改訂公式 と呼ばれる方は

$$k_b=\dfrac{-1+\sqrt{1+4\alpha\subsc{t} \pi^2}}% {2 \alpha\subsc{t} \pi^2}$$ (6.68)

となる。ここの $\alpha\subsc{t}$は，式(4.85a)で定義した せん断変形の影響を表すパラメータである。 この2者の違いは，断面力としてのせん断力の 構成則をどのようにモデル化するかの違いに依る。 改訂公式の方はつるまきバネのような部品の公式として知られ，Engesserの 公式の方が棒の力学理論と考えられている。

パラメータ $\alpha\subsc{t}$は細長比の逆数の2乗に相当して いたから，この平方根の逆数を横軸にとって 座屈係数を整理して図-6.49に 示した。 つまり横軸の左に行くほど短い梁-柱になるが， かなり短い場合にEuler荷重 から数十%の低減が見られる。 $\alpha\subsc{t}$は 材料定数比 $(\slfrac{E}{G})$にも比例しており，長い柱で あってもせん断抵抗が比較的小さい場合には 座屈荷重が低下する。ただし上の二つの公式による違いは 僅かである。さらに，このくらい短い柱の場合には伸びの影響も比較的 大きくなるが，これについても参考文献[37]等を参照して欲しい。

6.5.4 弾性床上のTimoshenko梁-柱の座屈

以上の二つの状況が重なった状態，つまり 弾性床上のTimoshenko梁-柱の場合にはさらに面白い 結果を示す。これも詳細は参考文献[37]等を 参照して欲しいが，Engesserの公式に対応する理論の枠組の中での つり合い式 を無次元化して示すと

$$\left(1-\pi^2 k \alpha\subsc{t}\right)\overline{w}'''' +\left(\pi^2 k-s_w \alpha\subsc{t}\right)\overline{w}'' +s_w w=0$$

となる。 $\alpha\subsc{t}=0$としたものは式(6.64)になる。 ここに

$$\overline{w}\equiv\dfrac{w}{\ell}, \quad ( )'\equiv \D*{}{\xi}, \quad \xi\equiv\dfrac{x}{\ell}$$

は節-4.6.2でも用いた無次元量である。また境界条件 は

$$\begin{eqnarray*} \overline{w} & = & \mbox{与える}\quad \mbox{あるいは} \quad ... ...overline{w}'' +\alpha\subsc{t} s_w \overline{w}=\mbox{与える} \end{eqnarray*}$$

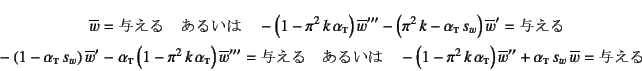
と表される。

図 6.50: 弾性床上のTimoshenko梁の座屈荷重

一例として， 両端単純支持梁-柱の固有値問題を解くと，その座屈係数が

$$k_b= \dfrac{\left(n\pi\right)^4+s_w \alpha\subsc{t}\left(n\... ...ft(n\pi\right)^2+\alpha\subsc{t}\left(n\pi\right)^4\right\}}$$ (6.69)

となる。 この関係を示したのが図-6.50であるが， 弾性床の反力係数$s_w$は図中の値$s_w=200$に固定した。 横軸は座屈モードの次数$n$であり，縦軸が式(6.69)の 座屈係数である。各$n$での値を線で結ぶことに意味は無いが， 同じ $\alpha\subsc{t}$毎に線で繋いで区別し易くした。 線の横の数字が $\slfrac{1}{\sqrt{\alpha\subsctiny{t}}}$の値である。 それが $\slfrac{1}{\sqrt{\alpha\subsctiny{t}}}=10$くらい 細長い場合（一番上の実線）には， 普通の梁-柱と同様高次モードになるにつれて座屈荷重が単調に 増大している。しかし $\alpha\subsc{t}$の値が大きくなり， より短いTimoshenko梁-柱あるいはせん断抵抗の弱い 柱になるにつれて，高次モードの座屈荷重の方が最小値を持つようになる。 しかも $\slfrac{1}{\sqrt{\alpha\subsctiny{t}}}=4$以下になると， 異なるモードの座屈荷重がほぼ同じレベルになるのも 大きな特徴である。こういった現象は塑性座屈等（例えば 粘土の3軸圧縮試験供試体に生じるせん断帯）にも見られ， 同じ荷重レベルであっても，現れるせん断帯のパターン（座屈モード）が 試験片によって異なることがある。 これはとても重要なことで，いわゆるEuler座屈が座屈の本質だと 思い込んではいけないことを示唆している。

最新版を正確に読むためには pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。