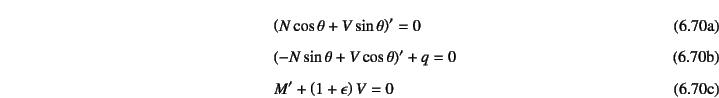
(6.70)
最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
前節までは比較的小さい変位状態での理論を誘導して用いたため,座屈後の
挙動については予測することができなかった。
ここでは,大きく変位するものの材料は弾性を保持する範囲での
棒理論を紹介し,柱の座屈後の挙動について
概説する。図-6.17のような変位した状態での
つり合いを考え,式(6.21)を誘導したときに
使った微小たわみ角の近似を用いなければ支配方程式6.11を求めることができる。
したがって三角関数がそのままの形で残り,結局,
つり合い式が
となる。ここに![]() は軸線の伸びひずみで
は軸線の伸びひずみで
と定義した。元々単位だった軸線微分要素が
変位したあとの長さが![]() になることは,
ピタゴラスの定理
からも理解できるだろう。同様に,境界条件は
になることは,
ピタゴラスの定理
からも理解できるだろう。同様に,境界条件は
となる。一方,たわみ角と変位の関係は
となっている。たわみ角![]() が小さく,伸びひずみが非常に
小さく
が小さく,伸びひずみが非常に
小さく
![]() と考えれば,
上式は
と考えれば,
上式は![]() と近似できて,
微小変位理論の関係式(4.4)に一致する。
と近似できて,
微小変位理論の関係式(4.4)に一致する。
断面力と変位の関係は,Bernoulli-Euler梁の場合は近似無しに 微小変位理論のそれと同じ表現で
(6.74)
となるが,![]() は式(6.71)で定義した軸の伸びである。
また
は式(6.71)で定義した軸の伸びである。
また![]() は軸の曲率で
は軸の曲率で
と定義される。 以上の式で境界値問題として棒の非線形問題を記述できる。 ただし,限定された問題以外は 何らかの数値解析法6.12を用いない限り, 解を得ることは不可能である。
ちなみに,
梁-柱理論程度に変位が比較的小さい場合,
式(6.71)の変位勾配の2次項までで
と近似でき,さらに第2項は第1項にくらべて高次項で無視できると
近似することによって,上式の右式のように,
式(6.29b)の関係を得る。
また式(6.55) (6.75)から
となるが,これも伸びひずみが非常に小さくかつ比較的変位が小さい
梁-柱理論程度の変位レベルでは,微小変位理論のそれと
同様
![]() と近似していいことがわかる。
と近似していいことがわかる。
大きく変位する棒の支配方程式は強い非線形性を有しているため,
解析的に解くことは一般には困難である。
ただし,座屈点直後の挙動を摂動法
によって求めることは可能である。
方法については文献[14]に詳細に述べられているので,
ここには結果のみを列挙する。
まずこの章の最初に用いた図-6.3の棒を対象とする。
棒の回転角![]() を用いた全ポテンシャルエネルギは
を用いた全ポテンシャルエネルギは
| (6.76) |
となる。これを座屈点
![]() ,
,
![]() の近傍で摂動させる(具体的には第4変分まで求める)
ことによって,外力と回転角の最初の摂動
を
の近傍で摂動させる(具体的には第4変分まで求める)
ことによって,外力と回転角の最初の摂動
を
| (6.77) |
のように求めることができる。 この関係式は,図-6.4の厳密な曲線とほとんど重なってしまい, 区別がつかないくらいの精度になっている。
次に一様断面の両端単純支持梁のEuler座屈を対象としよう。
前節の大変位理論を踏まえれば,この系の全ポテンシャルエネルギは
| (6.78) |
と定義していい。![]() は式(6.71)で,
は式(6.71)で,![]() は
式(6.75)で定義されている。
これも座屈点
は
式(6.75)で定義されている。
これも座屈点![]() ,
, ![]() ,
,
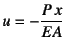 の
近傍で摂動させる(この場合も第4変分まで求める)と
の
近傍で摂動させる(この場合も第4変分まで求める)と
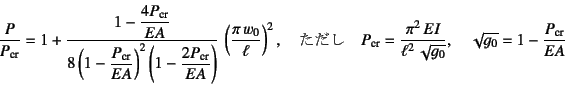 |
(6.79) |
のような関係を得る。ここに![]() はsine形状の座屈モードの振幅,
つまり単純支持梁中央の座屈後のたわみである。
通常は軸線の伸び
はsine形状の座屈モードの振幅,
つまり単純支持梁中央の座屈後のたわみである。
通常は軸線の伸び
![]() は単位量に比べれば
無視できるくらい小さいので,上式も実際には
は単位量に比べれば
無視できるくらい小さいので,上式も実際には
| (6.80) |
程度と考えてもいい。図-6.12にも示したように, 非常に平べったい放物線になっている。
式(6.71)で定義した軸の伸びが無い場合の
理論が,Elastica
と呼ばれる著名な棒理論である。
鋼等の構造材料でできた細長い棒が曲げを主に受ける場合,
この軸の不伸張の近似は実用的であることが知られている。
近似ではなく厳密に不伸張とするElastica理論では,
式(6.71)を用いて
という制約条件を課している。したがって必然的に
式(6.74a)の軸力の構成関係は無意味になるが,
つり合い式から![]() が無くなることはない。すなわち,
式(6.81)の付帯条件を満足するためには,
その反力としての軸力が,変形とは無関係に存在しなければ
ならなくなる。
ちょうど式(3.102)の非圧縮性(体積不変)流体の
応力ひずみ関係に,流体の変形とは無関係に静水圧
が無くなることはない。すなわち,
式(6.81)の付帯条件を満足するためには,
その反力としての軸力が,変形とは無関係に存在しなければ
ならなくなる。
ちょうど式(3.102)の非圧縮性(体積不変)流体の
応力ひずみ関係に,流体の変形とは無関係に静水圧![]() が存在しなければならないのと同じである。
したがって不伸張の棒の理論には,軸力の構成関係が
無くなった代わりに式(6.81)の制約条件が加わり,
その他の方程式は前節の有限変位理論のそれと見かけ上同じになる。
軸力
が存在しなければならないのと同じである。
したがって不伸張の棒の理論には,軸力の構成関係が
無くなった代わりに式(6.81)の制約条件が加わり,
その他の方程式は前節の有限変位理論のそれと見かけ上同じになる。
軸力![]() は変形とは無関係の独立した未知関数である。
変分原理で定式化する場合には,軸力
は変形とは無関係の独立した未知関数である。
変分原理で定式化する場合には,軸力![]() は,
式(6.81)の付帯条件を組み込むためのLagrangeの未定乗数
に相当する物理量6.13なる。
は,
式(6.81)の付帯条件を組み込むためのLagrangeの未定乗数
に相当する物理量6.13なる。
この理論で,先端に集中モーメント![]() が作用した片持ち梁を解くと,
任意点の変位成分が
が作用した片持ち梁を解くと,
任意点の変位成分が
と求められる。この場合のみ非線形微分方程式が容易に解ける。
結果は,図-6.51に示した
ように,
![]() で梁が真円になる。
また前節の柱を解くと,解が楕円積分
で表現される。
同様に片持ち梁のせん断の問題も楕円積分を用いて解を求めることができる。
詳細については,前者は例えば文献[73]等を,
後者は文献[10]等を参照のこと。
結果を図-6.51に示した。
いずれも縦軸が
で梁が真円になる。
また前節の柱を解くと,解が楕円積分
で表現される。
同様に片持ち梁のせん断の問題も楕円積分を用いて解を求めることができる。
詳細については,前者は例えば文献[73]等を,
後者は文献[10]等を参照のこと。
結果を図-6.51に示した。
いずれも縦軸が![]() あるいは
あるいは![]() の
外力レベルであり,横軸は棒先端の
の
外力レベルであり,横軸は棒先端の![]() 方向変位である。
方向変位である。
図-6.51の左の図が柱の圧縮である。
この章の最初に用いた回転バネと剛棒の
モデルと同じように,座屈荷重![]() 以上の圧縮力に
対する応答は安定で,外力の増加につれてたわみも増えている。
したがって材料が降伏しない限り,柱が座屈したあとも抵抗力を
保持しており,安定なつり合い状態になる。
ただ一般的な柱の場合には,座屈後のポテンシャルエネルギの
第4変分等が非常に小さいため,
小さい外力増分に対する変位増分が非常に大きくなってしまう。
この図でも
以上の圧縮力に
対する応答は安定で,外力の増加につれてたわみも増えている。
したがって材料が降伏しない限り,柱が座屈したあとも抵抗力を
保持しており,安定なつり合い状態になる。
ただ一般的な柱の場合には,座屈後のポテンシャルエネルギの
第4変分等が非常に小さいため,
小さい外力増分に対する変位増分が非常に大きくなってしまう。
この図でも![]() を越えるとすぐに
横軸
を越えるとすぐに
横軸
![]() が0.5程度に
まで達している。これに伴い発生するひずみも大きくなって
材料の弾性限界を越え,系の抵抗力を失うのが普通である。
が0.5程度に
まで達している。これに伴い発生するひずみも大きくなって
材料の弾性限界を越え,系の抵抗力を失うのが普通である。
次に,同じ図の右側の図が, 片持ち梁の先端にせん断外力を加えたときの応答である。 図中の一点鎖線が式(4.37a)で求めた線形応答である。 この場合には,幾何学的非線形性は剛性を大きくする効果を有しており, 次第に変位が線形理論のそれよりも小さくなっているのは興味深い。
一般に細長比がある程度大きい場合には,軸の伸び縮みは
単位量や曲げ変形に比べて無視できるくらい小さい。
したがってElastica理論で問題を解決できる場合もあり,
求められる解も軸の伸びを考慮した数値解等との差は非常に小さい。
せん断を作用させた片持ち梁の場合で具体的な数値を示すと,
細長比が10程度まで小さくなったと
しても,
![]() くらいの外力レベルでの
たわみ量が,Elasticaの解より1.5%増加する程度である。
しかしElasticaも解析解が存在するのはこの3例くらいで,
結局は何らかの非線形数値解析に頼らざるを得ない。
一つの方法を節-E.6.2に示しておいた。
くらいの外力レベルでの
たわみ量が,Elasticaの解より1.5%増加する程度である。
しかしElasticaも解析解が存在するのはこの3例くらいで,
結局は何らかの非線形数値解析に頼らざるを得ない。
一つの方法を節-E.6.2に示しておいた。
さて,
曲げ剛性![]() を無限大にして,棒の両端をヒンジで接合した
系をトラスとみなすことができるように,その逆の
を無限大にして,棒の両端をヒンジで接合した
系をトラスとみなすことができるように,その逆の![]() の
極限がケーブルや弦に相当することは容易に想像できよう。
ケーブルもその材料的な特長から,長大構造系には欠かせない
構造部材である。
有限変位理論を紹介したついでに,
前節の伸びない棒が曲げに抵抗できない場合の
支配方程式を求めておこう。
曲げ剛性を零にしたので,支配方程式中の曲げモーメントも
無視すればいい。前節と同様,軸線が伸びないことに対する反力と
しての抵抗力が
の
極限がケーブルや弦に相当することは容易に想像できよう。
ケーブルもその材料的な特長から,長大構造系には欠かせない
構造部材である。
有限変位理論を紹介したついでに,
前節の伸びない棒が曲げに抵抗できない場合の
支配方程式を求めておこう。
曲げ剛性を零にしたので,支配方程式中の曲げモーメントも
無視すればいい。前節と同様,軸線が伸びないことに対する反力と
しての抵抗力が![]() であるとすると,つり合い式(6.70)と
不伸張の条件式(6.81)とは
であるとすると,つり合い式(6.70)と
不伸張の条件式(6.81)とは
と書くことができる。ここで![]() は棒の単位長さ当たりの質量であり,
分布外力は棒の一様な自重
は棒の単位長さ当たりの質量であり,
分布外力は棒の一様な自重![]() のみとした。
のみとした。![]() は重力加速度である。
さらに
は重力加速度である。
さらに
と定義した![]() ,
, ![]() は,棒軸線上の任意点の変形後の位置
ベクトルの
は,棒軸線上の任意点の変形後の位置
ベクトルの![]() ,
, ![]() 方向成分である。
方向成分である。
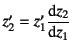 を用い,
式(6.82a)を考慮して式(6.82b)を
変形したものに,式(6.82c)から得ることができる
を用い,
式(6.82a)を考慮して式(6.82b)を
変形したものに,式(6.82c)から得ることができる

という関係を代入すると
![\begin{displaymath}
N \D*[2]{z_2}{z_1}\left\{1+\left(\D*{z_2}{z_1}\right)^2\right\}^{-1}
+ mg = 0 \eqno{(b)}
\end{displaymath}](s2img967.gif)
が曲げに関するつり合い式である。
一方![]() を適切に選んでやれば,式(a)から正の符号だけを
採用して
を適切に選んでやれば,式(a)から正の符号だけを
採用して
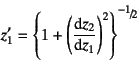
と置いてもいいから,これを式(6.82a)の軸方向のつり合い式に
代入した上で,式(b)を用いて整理すると
という軸力に関するつり合い式を得る。すなわち
となる。これを再度式(b)に代入し直して![]() を消去した
上で面倒な演算を続けると,最終的に得ることができるつり合い式は
を消去した
上で面倒な演算を続けると,最終的に得ることができるつり合い式は
となる。これはケーブルの変形後のつり合い形状![]() を支配する
方程式であり,この方程式の解は懸垂曲線
と呼ばれている。解の一般的な形は
を支配する
方程式であり,この方程式の解は懸垂曲線
と呼ばれている。解の一般的な形は
であり,定数![]() ,
, ![]() ,
, ![]() は両端の境界条件とケーブルの
長さから決定される[131]。
は両端の境界条件とケーブルの
長さから決定される[131]。
実は
この問題は変分問題の最も有名なものの一つでもある。そこで,
例えば文献[131]を参考にしてその問題を記述しておく。
不伸張であることから,つり合っている形状![]() での
ケーブルの全長が元の長さ
での
ケーブルの全長が元の長さ![]() に等しい条件は
に等しい条件は
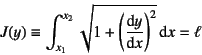
と表される。この式を付帯条件としながら,ケーブル全体の持つ
総ポテンシャルエネルギ
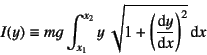
を最小にする問題が,ケーブルの形状決定問題の一つの数学的記述になる。
すなわち,Lagrangeの未定乗数![]() を用いた
を用いた
という変分原理のEuler方程式
が,式(6.84)の![]() を
を![]() に置き換えた
ものに一致する。その解の
懸垂曲線そのものを図-6.52に例示した。
ほとんど重なっているが,
参考のために破線で示したのは,ケーブル形状の両端の位置を
一致させた上で最下点の
に置き換えた
ものに一致する。その解の
懸垂曲線そのものを図-6.52に例示した。
ほとんど重なっているが,
参考のために破線で示したのは,ケーブル形状の両端の位置を
一致させた上で最下点の![]() 座標が同じ値になるようにした
放物線である。
座標が同じ値になるようにした
放物線である。
弦はケーブルと
同じものだが,力学理論としては,大きな張力
![]() で
引張られて直線状態にあるものが
微小変位の範囲で運動するものを対象としている。
すなわち式(6.30)の梁-柱理論程度の
変形・変位の範囲で,曲げ剛性が零になったものと考えていい。
つまり式(6.30)で
で
引張られて直線状態にあるものが
微小変位の範囲で運動するものを対象としている。
すなわち式(6.30)の梁-柱理論程度の
変形・変位の範囲で,曲げ剛性が零になったものと考えていい。
つまり式(6.30)で![]() とした上で,
とした上で,![]() を零と置いた
を零と置いた
がそのつり合い式
になる。
これは式(6.82)で![]() として
として![]() ,
, ![]() の2次項を
無視して求められる
の2次項を
無視して求められる
と等価である。
もしこれが運動していれば,Newtonの法則から
が運動方程式
になる。ここに![]() は棒の単位長さ当たりの質量であり,
上に付したドットは時間微分である。
さらに分布外力が零であれば,上式は
は棒の単位長さ当たりの質量であり,
上に付したドットは時間微分である。
さらに分布外力が零であれば,上式は
と変形でき,式(3.99)と同じ波動方程式
になる。つまり弦を伝わる波の速度が
であることを示している。ここに![]() は弦の密度である。
は弦の密度である。